基于Kalman滤波算法的陀螺仪动态漂移补偿研究

马正华，卢成俊，戎海龙，贺小捧

(常州大学 信息科学与工程学院， 江苏 常州 213000)



基于Kalman滤波算法的陀螺仪动态漂移补偿研究

马正华，卢成俊，戎海龙，贺小捧

(常州大学 信息科学与工程学院， 江苏 常州 213000)

应用MEMS陀螺仪测量人体手臂运动姿态时，针对陀螺仪受线加速度干扰导致测量姿态发散的问题，提出基于Kalman滤波算法的姿态误差补偿方法；该方法首先将陀螺仪采集到的角速度通过方向余弦算法解算得到姿态角，并将陀螺仪动态漂移造成的姿态角误差视为时变信号，通过建立姿态角漂移误差的状态方程及观测方程，应用卡尔曼滤波算法，实现对姿态角漂移误差的估计，最终达到对陀螺仪动态漂移误差的补偿；实验与仿真结果表明，应用该算法能够有效的抑制线加速度干扰导致的陀螺仪测量的姿态发散，适用于陀螺仪对人体手臂运动姿态的测量。

姿态测量；方向余弦算法；卡尔曼滤波算法；姿态补偿

0 引言

获取真实准确的人体运动姿态信息是对人体开展生物力学方面的研究和对人体的各种运动信息进行检测、跟踪以及统计分析的基础。MEMS惯导器件由于体积小、成本低、易于数字化和动态测量特性良好等优点成为人体姿态测量的理想选择[1-3]。对陀螺仪输出进行积分便能得到姿态信息[4]，而由于本身特性的限制， MEMS陀螺仪的输出噪声以及随机漂移导致解算得到的姿态产生漂移误差[5-6]，并随时间推移而累积增大，因此陀螺仪通常与其他姿态传感器组合使用获得稳定可靠的姿态信息。目前传统的方法是采用融合算法，以加速度传感器、地磁传感器输出姿态角来修正陀螺仪的输出。

Sabatini AM提出了一种VSD-EKF(variable-state imension extend kalman filter)算法,该算法假设目标物体在缓慢移动,即假设载体没有线加速度干扰,用 MARG 传感器估计人体三维姿态信息,但该算法解算精度只排除了环境磁场影响和陀螺仪随机误差影响,没有考虑到人体姿态变化带来的加速度变化导致加速度计干扰的情况[7]。文献[8]采用的测量融合方法将加速度传感器和陀螺仪传感器数据进行加权平均，可应用于动态环境，但测量精度不高。Rehbinder H等人[9]基于陀螺仪和加速计两种类型的传感器，提出了一个姿态解算算法，但由于缺少磁强计信息，而使得航向角的累积误差不能得到消除。文献[10]通过建立加速度和陀螺仪的误差数据模型，采用卡尔曼滤波方法预测飞行器的飞行姿态，能够较好抑制陀螺仪漂移造成的姿态发散，但不适用于运动状态变化较快的场景。文献[11]和文献[12]采用了融合了加速度计和地磁计的扩展卡尔曼(EKF)算法，但在载体存在线加速度时，加速度传感器给出的是运动加速度和重力加速度的叠加值，此时计算出的载体姿态角就有较大的误差；同时在室内使用地磁计时特别容易受周围环境的干扰而产生随机误差，影响磁强计的输出[13]。

由于人体姿态运动的特殊性譬如人体手臂运动，运动时常常伴随着短时间内线加速度有较大幅度变化等情况。在这种情况下，由于加速度计输出的信息既包含重力加速度信息又包含运动加速度信息，导致采用融合算法受加速计输出信息不准确的影响其解算得到的姿态信息其与实际姿态信息存在很大误差[14]。因此本文针对以上融合算法在线加速度干扰情况下手臂姿态解算误差较大的问题，采取单独使用陀螺仪的输出信号解算姿态，避免引入加速度计和地磁计受干扰的数据。而在利用陀螺仪对运动载体姿态进行测量时，载体线加速度能够使陀螺仪产生漂移[15]，进而产生姿态误差，即载体姿态漂移程度与陀螺仪所测载体的运动复杂度有关[16]。因此，本文将姿态漂移误差视为时变信号，认为该姿态漂移误差大小与上一时刻的的姿态漂移误差大小及当前时刻姿态角的变化量相关，据此建立陀螺仪姿态漂移误差状态方程；选取陀螺仪输出姿态角的低通滤波作为陀螺仪姿态漂移误差观测方程，在此基础上，应用卡尔曼滤波算法，对姿态漂移误差进行估计，从而达到补偿姿态误差，提高惯性器件测量手臂运动姿态精度的目的。

1 关于四元数与方向余弦矩阵的姿态角分析

通常将惯性测量单元固定安装在运动载体上，由运载体的机体轴确定的坐标系一般称之为载体坐标系b，与之相对应的惯导系统所采用的坐标系称为导航坐标系n。确定载体的姿态和航向实际上就是确定载体坐标系相对于导航坐标系的方位关系。而载体坐标系相对于导航坐标系的转换可以通过四元数法或者欧拉角法实现，由于四元数法可以避免欧拉角法的奇异问题，因而被广泛采用。经3次旋转后的导航坐标系和机体坐标系之间的坐标关系可由一个矩阵来表示，即方向余弦矩阵：

(1)

利用四元数可确定出导航坐标系至载体坐标系的方向余弦矩阵:

(2)

(3)

(4)

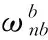
由 式(1)(2)便可求得姿态角：

(5)

2 卡尔曼滤波器的设计

本文将陀螺仪动态漂移造成的姿态误差视为时变信号，并建立相应的状态方程和观测方程，通过卡尔曼滤波得到较为准确的姿态误差估计值，从而补偿姿态角的误差。图1所示为卡尔曼滤波过程设计框图。

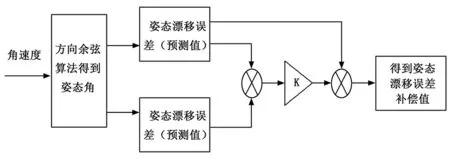
图1 卡尔曼滤波过程设计框图

2.1 陀螺仪姿态漂移误差的状态方程

利用陀螺仪测量手臂运动姿态，陀螺仪传感器信号经过AD转换器变成计算机可处理的数字信号。在使用这些数字信号进行手臂姿态解算前还应补偿陀螺仪的静态随机漂移，以减少陀螺仪静态随机漂移对姿态解算造成的影响。经过处理后陀螺仪角速度通过方向余弦算法便可得到三轴姿态角。由于线加速度的干扰造成陀螺仪输出的漂移，解算得到的姿态角与实际姿态存在一个姿态漂移误差，即在k时刻，实际姿态角与解算得到的姿态角存在如下关系：

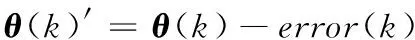
(6)

式中,θ(k)′为k时刻实际姿态角，θ(k)为k时刻陀螺仪输出的角速度通过方向余弦算法解算得到的姿态角，error(k)为k时刻的姿态漂移误差。

在利用陀螺仪对运动载体进行测量时，载体线加速度使陀螺仪产生漂移造成的姿态误差，与陀螺仪所测载体的运动复杂度有关[16]。本文将该运动复杂度描述为k时刻姿态角相对于k-1时刻姿态角的变化量，并认为由陀螺仪漂移带来的姿态误差是累积的，据此建立姿态漂移误差模型方程：

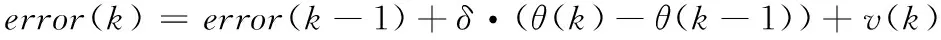
(7)

其中:error(k)为k时刻的姿态漂移误差，error(k-1)为k-1时刻姿态误差，δ为某一常数。按照以下方式选取系统状态矩阵X=errork，A=I，B=δ，控制量u(k)=θ(k)-θ(k-1)，便可建立姿态漂移误差的状态方程：

(8)

2.2 陀螺仪姿态漂移误差的观测方程

陀螺仪传感器输出的是角速度，当静置时，陀螺仪输出的角速度便是陀螺仪的静态漂移。而当陀螺仪测量运动载体时，陀螺仪输出的是载体的角速度，由线加速度导致的陀螺仪动态漂移无法直接测量得到，因此可将角速度经积分变为姿态角，通过姿态角误差来表征载体运动时陀螺仪的漂移情况。本文采用陀螺仪在k时刻及k时刻前几个时刻解算得到的姿态角之间的低通滤波，作为陀螺仪漂移造成的姿态漂移误差的观测量，即姿态漂移误差观测量为：

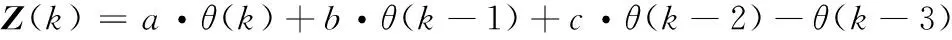
(9)

其中:k为采样时间，a、b、c为某一常数，满足a+b+c=1，θ(k)、θ(k-1)、θ(k-2)、θ(k-3)分别为陀螺仪在k、k-1、k-2、k-3时刻解算得到的姿态角。

2.3 Kalman滤波算法的实现

基于以上姿态漂移误差的状态方程和观测方程应用Kalman滤波算法，以对姿态误差进行估计，从而达到补偿姿态，提高惯性器件测量手臂运动姿态精度的目的。

卡尔曼滤波过程分为以下几步实现：

1)首先由陀螺仪输出的k时刻、k-1时刻的角速度通过方向余弦算法得到对应时刻的姿态角θ(k)、θ(k-1)，则由(7)式可得姿态漂移误差的状态方程：

error(k/k-1)=error(k-1/k-1)+δ·(θ(k)-

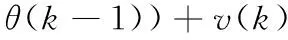
(10)

可估计得到k时刻利用上一状态预测的结果，其中error(k-1/k-1)是k-1时刻的姿态漂移误差最优的结果，设定0时刻的error(0)为0，δ的值为某一常数。

2)更新对应于error(k/k-1)的协方差：

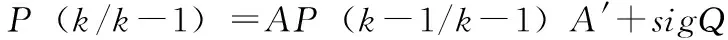
(11)

其中:A=I，P(k-1/k-1)是error(k-1/k-1)对应的协方差，sigQ是系统过程的协方差。

3)计算卡尔曼增益：

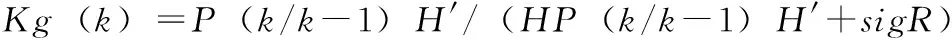
(12)

其中:H=I，sigR为观测方程系统过程协方差。

4)更新k时刻姿态误差的最优估计：

error(k/k)=error(k/k-1)+Kg(k)(Z(k)-

(13)

其中:Z(k)是姿态误差的观测值。

5)更新k时刻error(k/k)的协方差：

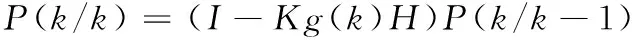
(14)

这样，就基本完成k时刻Kalman滤波算法的所有计算，k时刻姿态漂移误差的最优估计error(k/k)的大小即为姿态角需补偿的大小。当系统进行到k+1时刻，回到第1步进行计算，式(12)和式(14)保证滤波算法的持续性与递归性。

3 实验与仿真研究

为验证以上基于Kalman滤波的陀螺仪动态漂移补偿算法的有效性，实验选用了Xsens公司提供的惯性测量单元MTi10系列传感器模块来采集实验数据，MTI惯性测量单元包括三轴陀螺仪、三轴加速度计和三轴磁强计，本实验仅选取其中三轴陀螺仪的输出数据。同时，实验还采用POLHEMUS公司提供的LongRanger电磁跟踪系统，该装置能对载体空间姿态进行精确测量，可作为惯性系统姿态输出的对照基准。根据选用的测量单元，由官方手册资料查询得到陀螺仪的标准差为0.006rad/s，MTI惯性测量单元和LongRanger电磁跟踪系统采样频率分别是256Hz和240Hz。实验所做的手臂运动可以描述为：手握测量装置在近似水平面内做圆周运动，同时手部也做一定的角度摆动，运动约10s左右后，停止动作，并将手臂恢复至初始姿态。

基于采集的数据，并根据MTI惯性测量单元与电磁跟踪系统装置的采样频率的不同对采集的数据作出必要的处理后，得到图2所示陀螺仪采集的实测数据解算出的姿态变化曲线同电磁跟踪系统实测数据解算出的实际姿态变化曲线的对比。可以看到，横滚角的陀螺仪漂移最为明显，10s后姿态解算误差最大已经达到10°，这是因为，手部摆动运动带来了线加速度，而线加速度的干扰导致了陀螺仪漂移，进而导致解算出的姿态开始发散；俯仰角和偏航角方向受线加速度干扰影响较小，由陀螺仪解算得到的姿态信息大体体现了手臂实际运动姿态，但由于陀螺仪的随机漂移影响，其姿态累计误差在逐渐增大，所得的姿态信息在缓慢发散。

图2 陀螺仪解算得到的姿态与电磁跟踪系统得到的
实际运动姿态变化曲线对比

图3所示为经本文算法补偿过的姿态曲线与陀螺仪采集的实测数据解算出的姿态曲线和电磁跟踪系统解算得到的实际运动姿态曲线的对比。可以看到，经本文算法补偿过后，横滚角姿态发散情况得到抑制，其解算误差缩小在3°左右，姿态测量精度相比使用本文算法前得到提高，体现了本文算法在补偿由于陀螺仪动态漂移导致姿态误差的有效性；同样地，俯仰角和偏航角的姿态解算误差相比原先缩小在1°左右，测量精度也得到一定提高。

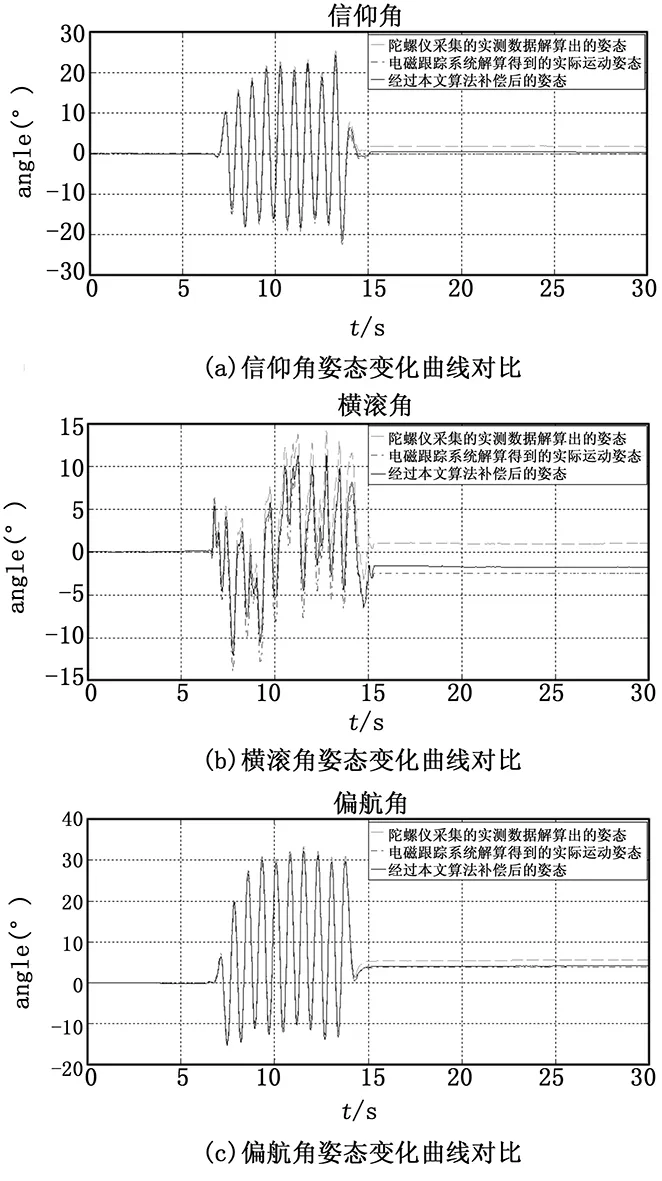
图3 加入本文算法补偿后姿态变化曲线对比

4 结论

应用MEMS惯导器件测量人体手臂运动姿态时，针对陀螺仪受线加速度干扰导致姿态发散的问题，本文介绍了一种基于Kalman滤波算法的姿态误差补偿方法。该方法将姿态漂移误差视为时变信号，据此建立陀螺仪姿态漂移误差的状态方程和观测方程，在此基础上，应用卡尔曼滤波算法，实现对姿态角漂移误差的估计，最终达到对陀螺仪动态漂移误差的补偿。实验与仿真结果表明，本文算法能够有效的抑制由线加速度干扰导致的陀螺仪测量的姿态发散，适用于陀螺仪对人体手臂运动姿态的测量。

[1]RoetenbergD,LuingeHJ,BatenC,etal.Compensationofmagneticdisturbancesimprovesinertialandmagneticsensingofhumanbodysegmentorientation[J].NeuralSystemsandRehabilitationEngineering,IEEETransactionson, 2005, 13(3): 395-405.

[2]VeltinkPH,SlyckeP,HemssemsJ,etal.Threedimensionalinertialsensingoffootmovementsforautomatictuningofatwo-channelimplantabledrop-footstimulator[J].Medicalengineering&physics, 2003, 25(1): 21-28.

[3] 李金凤, 王庆辉, 刘晓梅,等. 基于MEMS惯性器件的行人室内定位系统[J]. 计算机测量与控制, 2014, 22(11):3761-3763.

[4]MillerRB.Anewstrapdownattitudealgorithm[J].JournalofGuidance,Control,andDynamics, 1983, 6(4): 287-291.

[5] 王 帅, 魏 国. 卡尔曼滤波在四旋翼飞行器姿态测量中的应用 [J]. 兵工自动化, 2011, 30(1): 73-80.

[6] 秦永元，张洪钺，汪淑华.卡尔曼滤波与组合导航原理[M].西安：西北工业大学出版社，1998.

[7]SabatiniAM.Variable-State-DimensionKalman-basedFilterfororientationdeterminationusinginertialandmagneticsensors[J].Sensors, 2012, 12(7): 8491-506.

[8] 李媛媛, 张立峰. 多传感器自适应加权融合算法及其应用研究[J]. 自动化与仪器仪表, 2008(2):10-13.

[9]RehbinderH,HuX.Drift-freeattitudeestimationforacceleratedrigidbodies☆[A].RoboticsandAutomation, 2001.Proceedings2001ICRA.IEEEInternationalConferenceon[C].IEEE, 2001(4):4244-4249.

[10] 冯智勇, 曾 瀚, 张 力,等. 基于陀螺仪及加速度计信号融合的姿态角度测量[J]. 西南师范大学学报:自然科学版, 2011, 36(4):137-141.

[11]YunX,BachmannER.Design,implementation,andexperimentalresultsofaquaternion-basedKalmanfilterforhumanbodymotiontracking[J].Robotics,IEEETransactionson, 2006, 22(6): 1216-1227.

[12] 吴 杰, 闫建国. 基于修正的卡尔曼滤波的姿态估计算法研究[J]. 计算机仿真, 2012, 29(2):54-57.

[13]BirdJ,ArdenD.Indoornavigationwithfoot-mountedstrapdowninertialnavigationandmagneticsensors[EmergingOpportunitiesforLocalizationandTracking][J].IEEEWirelessCommunications, 2011, 18:28-35.

[14] 戎海龙, 戴先中, 刘信羽. 厨师手握锅具运动信息获取方法[J]. 仪器仪表学报, 2009 (11): 2291-2297.

[15]LiuC,ZhouZ,FuX.AttitudedeterminationforMAVsusingaKalmanfilter[J].TsinghuaScience&Technology, 2008, 13(5): 593-597.

[16]LambrechtS,JonkersI,PonsJL.Identificationanddecompositionoferrorin3Dmotioncaptureusinginertialandmagneticsensor.ConvergingClinicalandEngineeringResearchonNeurorehabilitationBiosystems&Biorobotics[Z]. 2013, 1: 721-725.

Research on Compensation of Dynamic Drift of Gyroscope Based on Kalman Filtering Algorithm

Ma Zhenghua，Lu Chengjun，Rong Hailong，He Xiaopeng

(College of Information Science and Engineering，Changzhou University，Changzhou 213000,China)

In order to solve the problem of attitude divergence caused by gyroscope which is interfered by the linear acceleration when use MEMS inertial navigation device to measure the attitude of the human arm movement, propose an attitude error compensation method based on Kalman filter algorithm. In this method, the attitude angle will be calculated first by angular velocity gyroscope output through direction cosine algorithm solution, through the establishment of the attitude angle drift error state equation and observation equation, attitude angle drift error will be estimated accurately and eliminated then. The experimental and simulation results show that , algorithm used in this paper can suppress the divergent attitude effectively and is suitable for gyroscope to measure the attitude of the human arm movement.

attitude measurement；direction cosine algorithm；Kalman filtering algorithm；attitude compensation

2016-03-19；

2016-04-25。

马正华(1962-)，男，江苏昆山人，教授，硕士研究生导师，主要从事嵌入式系统应用、计算机控制技术、电力电子技术等方向的研究。

1671-4598(2016)09-0191-04

10.16526/j.cnki.11-4762/tp.2016.09.054

TP3

A