岩石损伤软化的修正本构模型

李 博, 吴润江, 高为超

(西北核技术研究所,陕西 西安 710024)



岩石损伤软化的修正本构模型

李 博, 吴润江, 高为超

(西北核技术研究所,陕西 西安 710024)

利用服从Weibull分布的岩石微元强度表示方法,基于Drucker-Prager破坏准则,通过引入损伤变量的修正系数,利用应力-应变关系曲线峰值点处的应力、应变确定Weibull分布参数的关系式,建立不同围压下的损伤软化本构模型。该模型参数较少且易于确定,其参数的确定方法揭示了模型参数的物理意义。与前人的研究成果进行对比分析,结果表明该模型比未修正前有着明显的优越性,且与实测结果吻合较好,分析结果显示出该模型的合理性。

岩石; 损伤; 软化; 修正; 本构模型

0 引言

岩石损伤是指在加载条件下,由于岩石内部存在原始微观缺陷,其承载后又产生新的裂纹,并随荷载增加呈逐渐扩展趋势,岩石材料体积单元发生破坏、力学性能劣化的现象。岩石损伤主要指岩石内部微裂纹的形成、扩展和聚合。岩土材料的强度与应变关系可以通过损伤力学来解决,而岩石材料损伤本构关系可通过两种方式研究:一是以实验为基础,假设损伤变量与应力、应变服从某种关系,再以假设模型模拟试验所得应力-应变关系,建立损伤本构模型;二是根据岩石微元强度符合概率分布,先建立损伤变量与应力、应变之间的关系,进而建立起基于概率分布的本构模型[1-2]。

1 损伤变量与损伤本构关系

三轴试验通常为假三轴,取σ2=σ3,利用J.Lemaitre应变等效性假说[3]建立岩石损伤的本构关系[4]:

[σ*]=[σ]/(1-D)=[C][ε]/(1-D)

(1)

式中:[σ*]为有效应力矩阵;[C]为岩石材料弹性矩阵;[σ]为名义应力矩阵;[ε]为应变矩阵;D为岩石损伤变量。

假定岩石微元强度F服从Weibull分布[4-6],其概率密度函数可以表示为:

(2)

式中:F为微元破坏Weibull分布的分布变量;m、F0为Weibull分布参数。

岩石损伤变量D可定义为损伤面积与无损时材料全面积之比,考虑岩石材料损伤的随机性,岩石损伤变量D可表示为:

(3)

曹文贵等[2-7]率先提出基于岩石破坏准则的新型岩石微元强度度量方法,此方法较为合理,能反映应力状态对岩石微元强度的影响。由于Drucker-Prager破坏准则参数形式简单且适用于岩石介质而得到广泛应用,因此本文岩石微元强度采用该准则,即

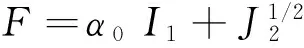
(4)

(5)

岩石微元体破坏前符合虎克定律,即:

(6)

利用式(1),并考虑式(6),由式(5)可得:

(7)

将式(7)代入到式(4)可得:

(8)

2 岩石损伤本构模型的建立及其参数的确定

2.1 岩石损伤本构模型的建立

谢和平[8]认为三维条件下损伤变量为一个代表性体积元素内的损伤等效面积与该截面总面积的比值,如果岩石材料各向同性,比值与截面方位无关,各应力分量的损伤程度相同,为同性损伤。但这只有理想岩石材料才满足,因此假设损伤情况满足Weibull分布是不合适的,本文尝试引入一个修正系数对1-D进行修正,使其能够反映岩石破裂后的残余强度特征。

利用式(1)及式(6)可得:

σ1=qEε(1-D)+2μσ3=

(9)式中:q为修正系数。

2.2 岩石损伤本构模型参数的确定方法

分别对式(8)、式(9)求导可得:

(10)

(11)

(12)

将式(12)代入到式(11)可得:

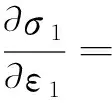
(13)

由式(13),并取峰值强度处F=Fc可得:

(14)

在峰值点处,将式(14)代入式(9)可得:

(15)

由式(15)可得:

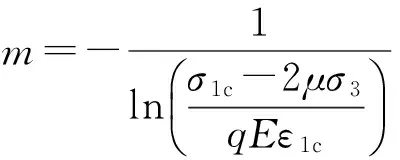
(16)

(17)

3 修正的岩石损伤本构模型的验证

为验证修正模型,引用文献[9]中的数据资料,岩石为大冶铁矿大理岩,可得其弹性模量E=25.34 GPa,泊松比μ=0.25,内摩擦角φ=25.73°,黏聚力c=23.9 MPa,单轴抗压强度σc=70.0 MPa。

将文献[8]中实验数据汇总,利用Fc、F0、m等的公式,可求出Fc和m值,F0用m表示。

在不同围压条件下,利用式(9)可求出σ1-σ3随应变ε1变化的关系式。试验曲线与理论曲线的比较图见图1。

从图1中可以看出不同的q值拟合所得的曲线图不同,但本文通过修正得出的拟合曲线与试验曲线比较接近,通过取不同q值的方法可以得到与试验曲线最为接近的拟合曲线。不同围压下的对比分析结果表明该修正方法相比q=1时的方法具有一定的优越性,但与实际试验曲线仍有一定程度上的出入,需要进一步地研究改进。

图1 试验曲线与理论曲线的比较Fig.1 Comparison between experimental and theoretical curves

4 结论

基于岩石破坏准则的岩石微元强度度量方法,从岩石微元强度服从Weibull分布的角度出发,通过对损伤变量进行修正,建立了不同围压下岩石损伤软化本构模型,并得出如下结论:

(1) 通过对损伤变量进行修正,建立起损伤软化本构模型,该模型能够反映岩石在复杂应力状态下变性破坏的全过程,尤其可反映岩石的软化特性;

(2) 该模型可通过峰值点应力、应变确定模型参数,使得模型参数的物理意义更加明确,增强参数计算的准确性,应用比较简便;

(3) 与未修正前模型的对比分析结果表明:该模型与试验曲线吻合较好,具有一定的优越性。

References)

[1] 杨友卿.岩石强度的损伤力学分析[J].岩石力学与工程学报,1999,18(1):23-27.

YANG You-qing.Continuum Damage Mechanics Analysis on Strength of Rock[J].Chinese Journal of Rock Mechanics and Engineering,1999,18(1):23-27.(in Chinese)

[2] 曹文贵,方祖烈,唐学军.岩石损伤软化统计本构模型之研究[J].岩石力学与工程学报,1998,17(6):628-633.

CAO Wei-gui,FANG Zu-lie,TANG Xue-jun.A Study on Statistical Constitutive Model for Soft and Damage Rocks[J].Chinese Journal of Rock Mechanics and Engineering,1998,17(6):628-633.(in Chinese)

[3] Lemaitre J.A Continuous Damage Mechanics Model for Ductile Fracture[J].J Eng Mater Tech,1985,107:83-89.

[4] 唐春安.岩石破裂过程中的灾变[M].北京:煤炭工业出版社,1993.

TANG Chun-an.Catastrophe in Rock Unstable Failure[M].Beijing:China Coal Industry Publishing House,1993.(in Chinese)

[5] Krajcinovic D,Silva M A G .Statistical Aspects of the Continuous Damage Theory[J].Int J Solids Structures,1982,18(7):551-562.

[6] Tang C A,Chen Z H,Xu X H,et al.A Theoretical Model for Kaiser Effect in Rock[J].Pure Appl Geophys,1997,150:203-215.

[7] 徐卫亚,韦立德.演示损伤统计本构模型的研究[J].岩石力学与工程学报,2002,21(6):787-791.

XU Wei-ya,WEI Li-de.Study on Statistical Damage Constitutive Model of Rock[J].Chinese Journal of Rock Mechanics and Engineering,2002,21(6):787-791.(in Chinese)

[8] 谢和平.岩石混凝土损伤力学[M].徐州:中国矿业大学出版社,1990.

XIE He-ping.Damage Mechanics of Rocks and Concrete[M].Xuzhou:China University of Mining and Technology Press,1990.(in Chinese)

[9] 林卓英,吴玉山,关玲莉,等.岩石在三轴压缩下脆—延性转化的研究[J].岩土力学,1992,13(2/3):45-53.

LIN Zhuo-ying,WU Yu-shan,GUAN Ling-li,et al.Research on the Brittle-ductile Transition Property of Rocks under Tri-axial Compression[J].Rock and Soil Mechanics,1992,13(2/3):45-53.(in Chinese)

A Modified Damage Softening Constitutive Model for Rock

LI Bo, WU Run-jiang, GAO Wei-chao

(NorthwestInstituteofNuclearTechnology,Xi'an710024,Shaanxi,China)

Using a rock micro-unit strength,which satisfies the Weibull random distribution and is based on the Drucker-Prager failure criterion,a correction coefficient for damage variables is introduced,which reflects the full stress-strain process and residual strength of rock.The relationship between Weibull distribution parameters under different confining pressures is established using the stress and strain at peak points on the stress-strain curve.A damage softening constitutive model of rock is then established,accounting for the rock triaxial stress-strain test curve.The model has few parameters,and the way of determining the parameters indicates the physical meaning of the model parameters.Compared with previous studies,this model,after modification,has obvious advantages.The rationality of the model proposed here is demonstrated using comparative analysis between the theoretical and experimental results.

rock; damage; softening; modified; constitutive model

2015-05-31

李 博(1986-)，男，助理工程师，主要从事岩土工程方面的研究。E-mail：libocare@126.com。

吴润江，主要从事构造地质学方面的研究。E-mail：future_wrj@yahoo.com.cn。

TU452

A

1000-0844(2016)05-0783-04

10.3969/j.issn.1000-0844.2016.05.0783