线性电路中基尔霍夫定理与戴维南诺顿定理的等效性研究

郑维民，苏成仁

(甘肃民族师范学院，甘肃 合作 747000)



线性电路中基尔霍夫定理与戴维南诺顿定理的等效性研究

郑维民，苏成仁*

(甘肃民族师范学院，甘肃 合作 747000)

通过计算和实验得出电工学中最基本的规律基尔霍夫定理与戴维南定理和诺顿定理具有等效性，它们对同一线性含电源电路有相同的结果。基尔霍夫定理不但能适合各种线性非线性有源无源电路的计算，且计算出的数据种类更齐全，这是戴维南定理和诺顿定理达不到的。但是戴维南定理和诺顿定理更适合实际测量中对电路的简化，它要比基尔霍夫定理更简便。

节点；回路；等效电阻；短路电流；开路电压

基尔霍夫定理、戴维南定理、诺顿定理是电工学的最基本规律，它是电工学理论的基石，它们都是解决有源或无源电路中电流电压问题的理论根据，这里用理论计算和实验证明的方法来证明基尔霍夫定理与戴维南诺顿定理具有等效作用，它们都可以解决有源或无源电路中电流电压问题，这一结论有助于电工课学习也能在实际电路分析中简化问题[1-3]。

1 三定理各自的表述和适应的对象

1.1 基尔霍夫定理

1.1.1 基尔霍夫电流定理：

电路中，在任何一个时刻，任何一个节点，流出(或流入)该节点电流的代数和恒等于零，

即∑I=0

(1)

式(1)中，若取流出节点的电流为正，则流入节点的电流为负。基尔霍夫电流定理反映了电流的连续性，说明了节点上各支路电流的约束关系，它与电路中元件的性质无关。它表明在节点上(电荷在没有被创造或消灭的情况下)电流守恒。

1.1.2 基尔霍夫电压定理：

在任何一个时刻，按约定的参考方向，电路中任一回路上全部元件两端电压的代数和恒等于零，

即∑U=0

(2)

基尔霍夫电压定理说明了电路中各段电压的约束关系，它与电路中元件的性质无关(既适用于线性也适用于非线性元件)[1]。它表述在回路中沿回路绕一圈电势的升降为零。

1.2 戴维南定理诺顿定理

1.2.1 戴维南定理

任何一个线性有源网络，总可以用一个理想电压源与一个等效内电阻的串联支路来代替。此理想电压源的电压等于该有源二端网络的开路电压IOC，其等效内阻RO等于该网络中所有独立电源均置零(理想电压源视为短路，理想电流源视为开路)时的等效电阻[2]。这一串联电路称为该网络的戴维南等效电路。

它表明在一个含电压源的线性网络中可以把网络看成是理想电压源和等效电阻的串联(它只适用于线性元件网络)。

1.2.2 诺顿定理

任何一个线性有源网络，总可以用一个理想电流源与一个等效电阻的并联组合来代替，此电流源的电流等于该有源二端网络的短路电流ISC，其等效内阻RO等于该网络中所有独立电源均置零(理想电压源视为短路，理想电流源视为开路)时的等效电阻。这一并联电路称为该网络的诺顿等效电路。

它表明在一个含电流源的线性网络中可以把网络看成是理想电流源和等效电阻的并联(它只适用于线性元件网络)。

从这里可以看出它们所对应的电路不同，但是通过下面的证明可以知道它们在线性电路中(由纯电阻组成的电路中)是等效的。

2 在基尔霍夫定理实验电路中证明戴维南定理诺顿定理与基尔霍夫定理的等效性

2.1 用基尔霍夫定理证明

在图1的电路(它是基尔霍夫实验专用电路)中,E1=6V,E2=12V,R1=510Ω,R2=1000Ω,R3=510Ω,R4=510Ω,R5=330Ω,求通过R3的电流I3,R1的电流I1,的电流I2。

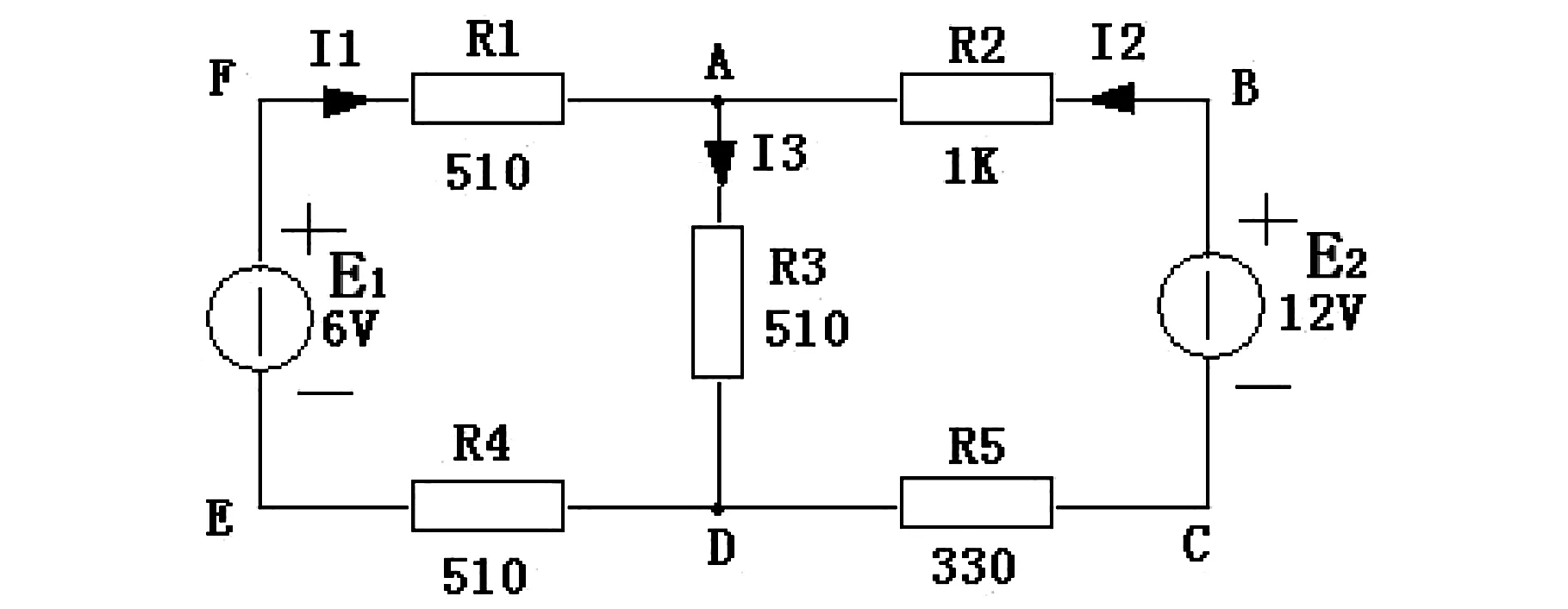
图1 基尔霍夫电路图

先用基尔霍夫定理求解：

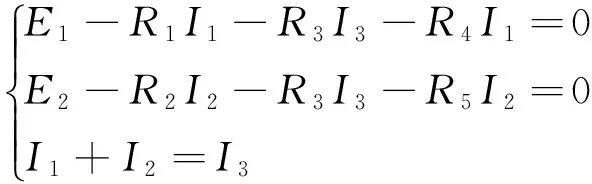
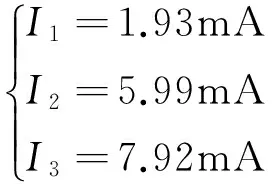
2.2 再用戴维南定理诺顿定理证明

先把R3支路单独划出来，如图2(a)所示。再求有源二端网络的戴维南等效电路。

由图2(b)求出开路电压UOC.[3]

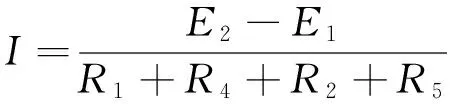
所以开路电压

等效电阻R0如图2(c)所示

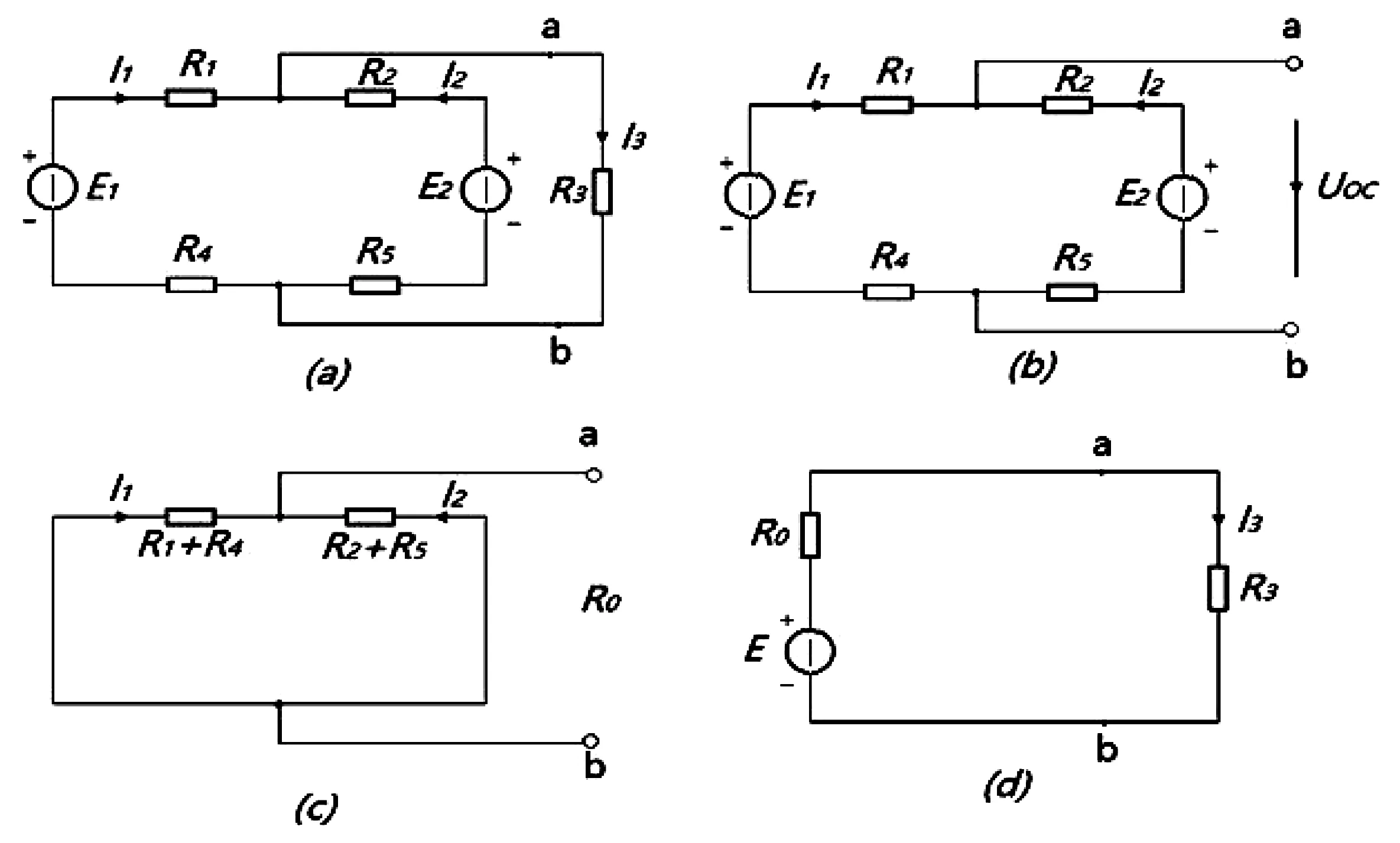
图2 戴维南电路图

=577.28Ω

等效电路电流的计算由戴维南等效电路图2(d)所示，

根据I3=7.91mA

得U3=I3R3=7.9146×10-3×510=4.04V

代入数据6-4.04=2×510I1

所以I1=1.93mA

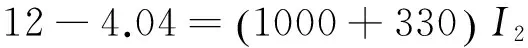
所以I2=5.99mA

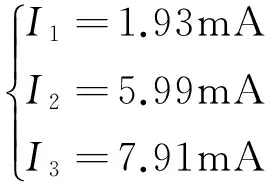
由计算结果可以看出，用基尔霍夫定理计算与戴维南定理计算是一样的，它们是等效的。

2.3 用实验测量证明

用基尔霍夫定理实验验证装置(电路图如图1所示)测量的数据如下：

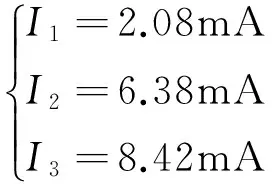
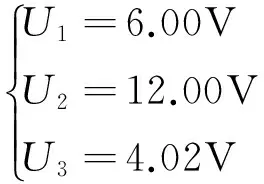
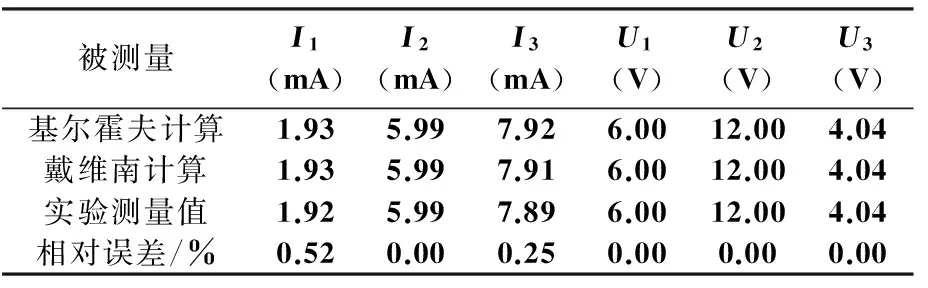
表1 两种计算和实验值对比

由对比表可以看出，用基尔霍夫计算定理与用戴维南定理计算的结果几乎一样，都与实际测量值相差无几,所以基尔霍夫计算定理与戴维南定理有等效作用。

3 在戴维南诺顿定理实验电路中证明戴维南定理诺顿定理与基尔霍夫定理的等效性

用计算戴维南诺顿定理简化(电压源短路，电流源开路)，图3简化为图4，它的等效电阻为：

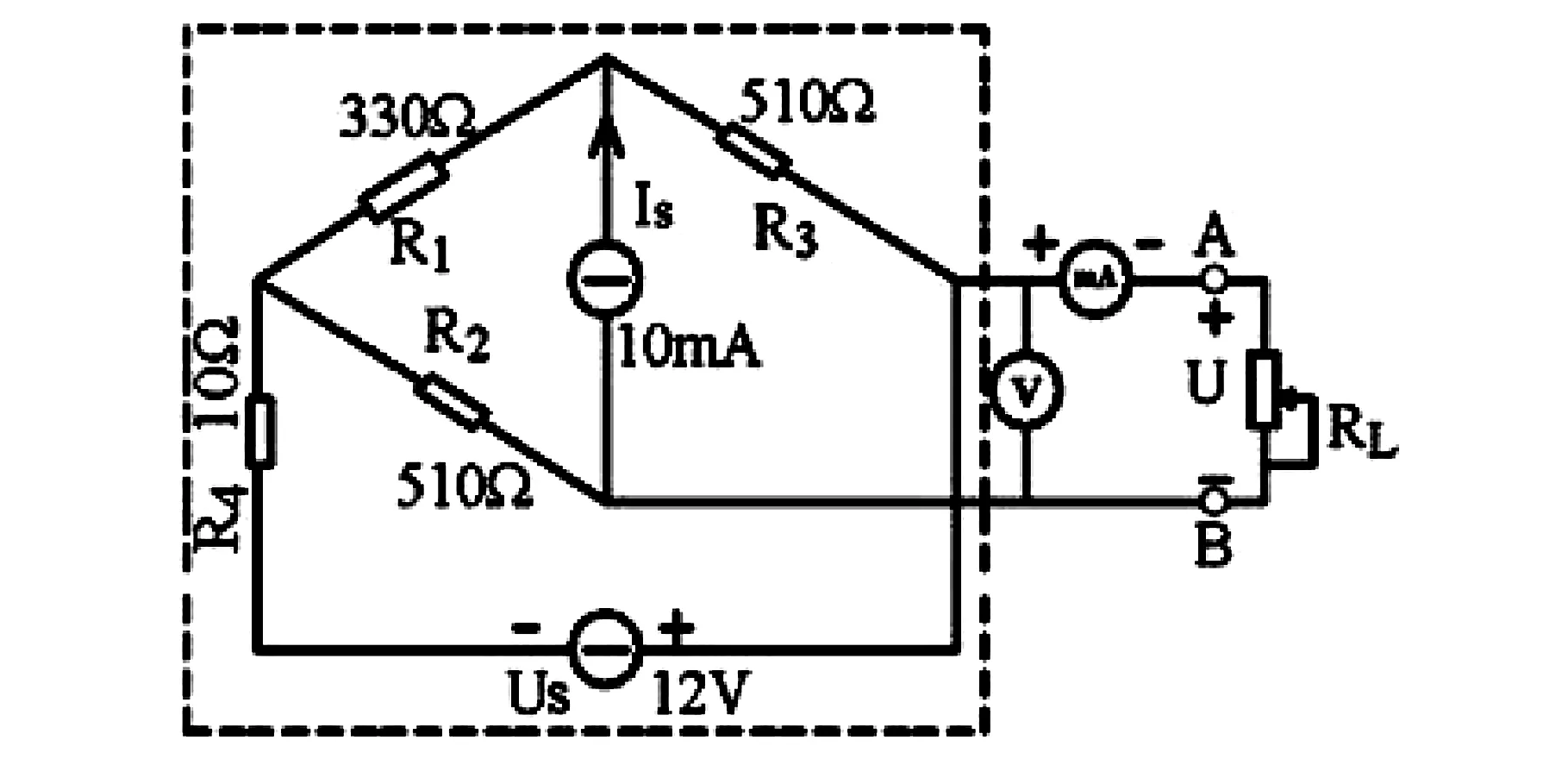
图3 戴维南定理诺顿定理实验电路

用基尔霍夫定理简化图3，开路电压如图5所示。

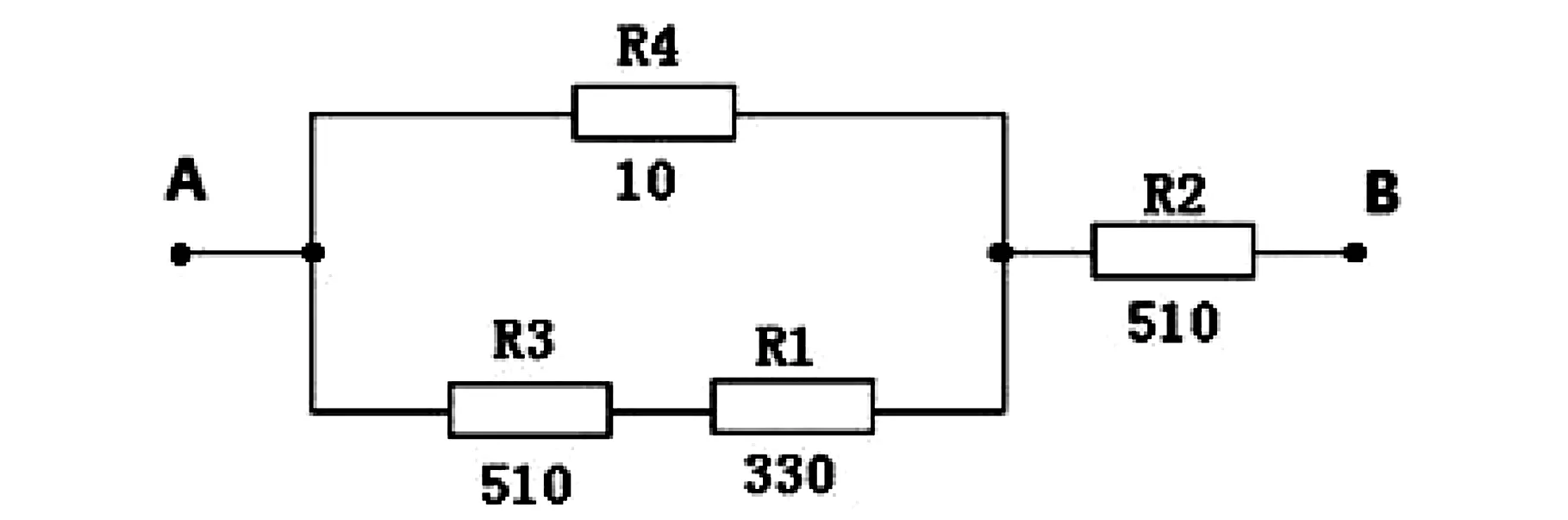
图4 戴维南定理诺顿定理实验电路的简化

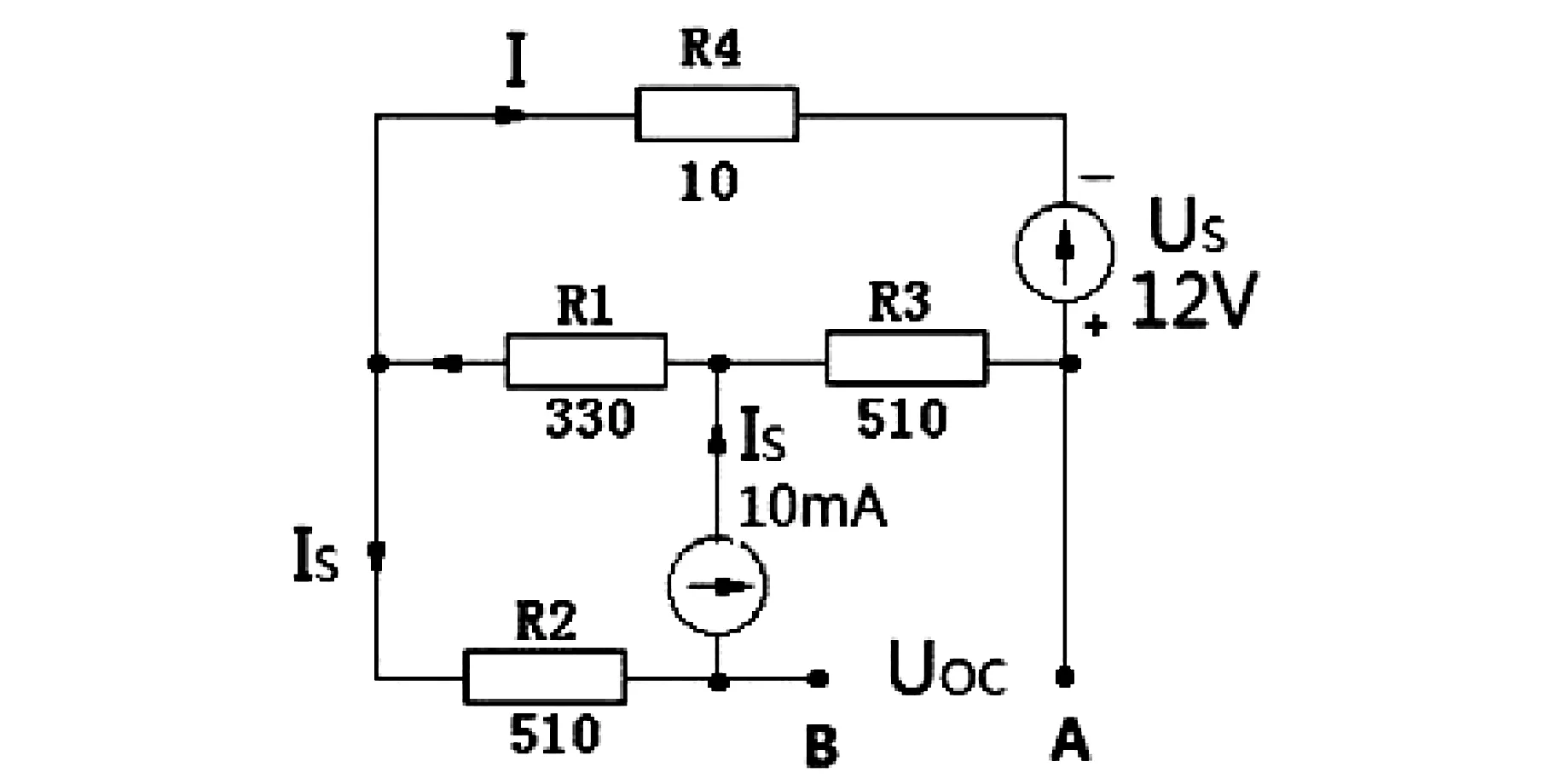
图5 开路电压

从开路电压图中按基尔霍夫定理有

代入数据

求解I=0.010235291A=10.24mA

所以开路电压

其中 UBA=-UAB=-UOC=17V

用基尔霍夫定理简化图3，短路电流如图6所示。

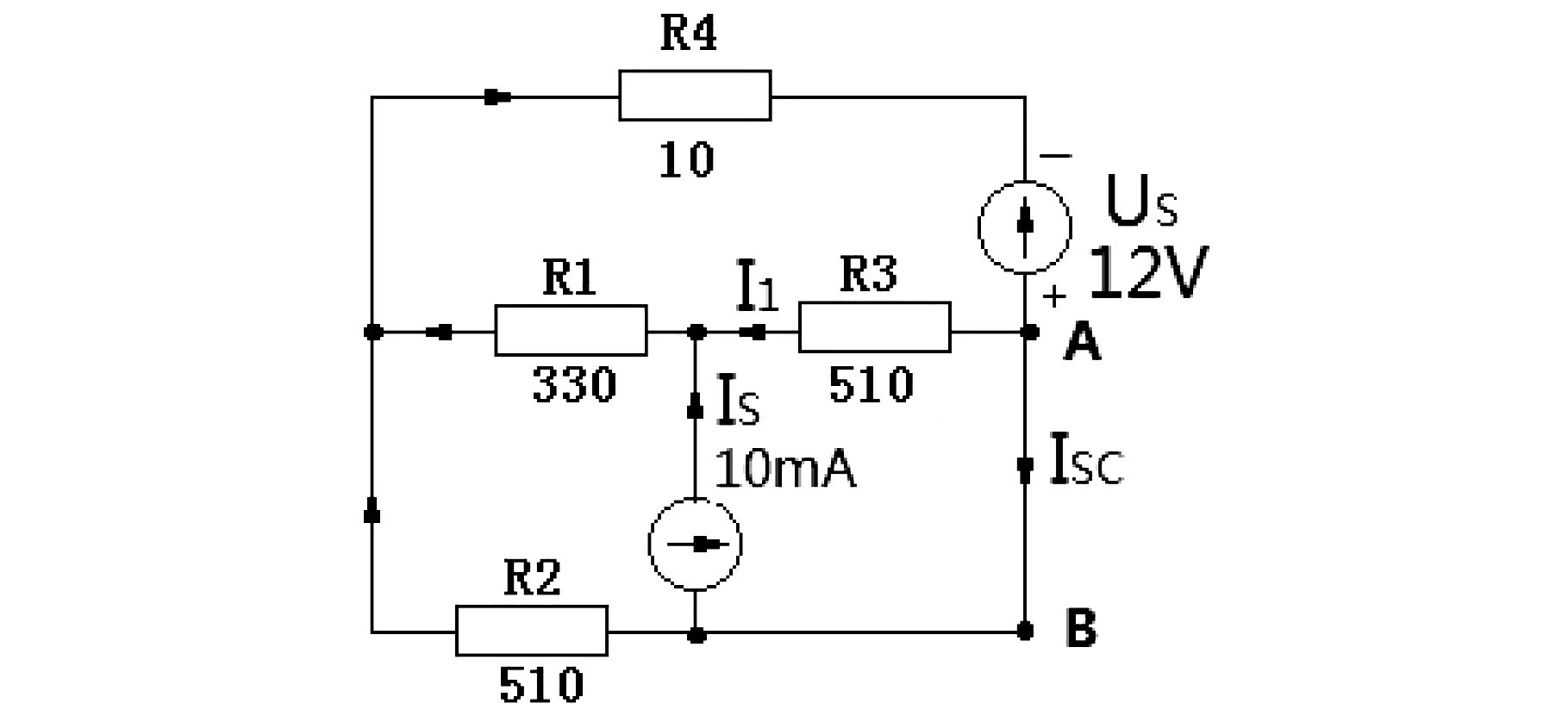
图6 短路电流

从短路电流图中按基尔霍夫定理有

代入数据得

求解得 ISC=0.03269518A=32,70mA

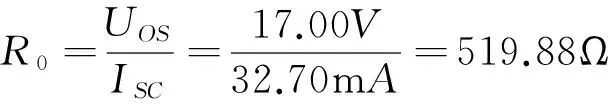
实验验证：按图7接入稳压电源US=12 V和恒流源IS=10 mA，不接入RL。用开路电压、短路电流法测定戴维南等效电路的UOC、R0和诺顿等效电路的ISC,R0。测出UOC,ISC并计算出R0(测UOC时，不接入直流毫安表)。

表2 用开路电压、短路电流法测定

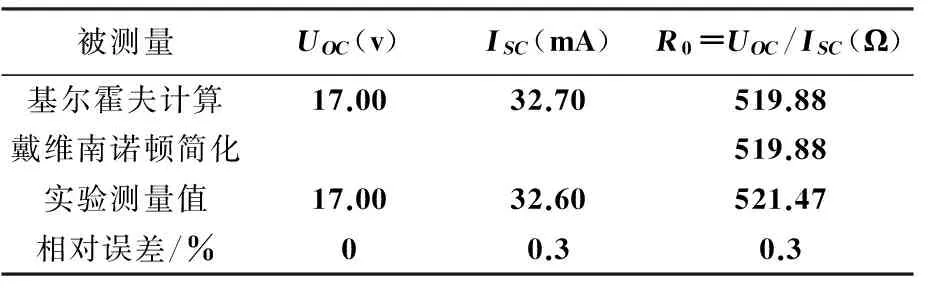
表3 基尔霍夫定理与戴维南诺顿定理两种计算和实验值对比

4 结 论

1.由上面的计算和实验知道，基尔霍夫定理与戴维南诺顿定理在线性有源无源电路的计算中具有等效性。

2.基尔霍夫定理与戴维南诺顿定理相比能适合各种线性非线性有源无源电路，计算出的数据种类更齐全，这是戴维南诺顿定理达不到的。

3.是戴维南诺顿定理更适合实际测量中电路的简化，它要比基尔霍夫定理更简便。

[1] 易沅屏.电工学[M].高等教育出版社.1993.

[2] 贺汉平，汤放奇.戴维南定理对含受控源电路的新分析法[J].株洲工学院学报,2000(4):29-30.

[3] 梁永清,韦东梅,韦忠海.戴维宁—诺顿定理的推广应用[J].电气电子教学学报,2015(2).

[4] 陈文娟，等.基于无线供电的旋转式LED点阵显示演示仪[J].大学物理实验，2015(2)：45-48.

[5] 王锦辉，等.桓流源作为惠斯容电桥电源的灵敏度研究[J].大学物理实验，2015(3)：69-71.

Research on Equivalence of the Kirchhoff Law and the Thevenin’s/Norton’s Theoremin the Linear Circuit

ZHENG Wei-min,SU Cheng-ren

(Gansu Normal University for Nationalities,Gansu Hezuo 747000)

It shows that the equivalence of the Kirchhoff’s Law and Thevenin/Norton’s theorem through the calculation and experiment,they have the same results on the same linear power circuit.Kirchhoff’s Law can not only suitable for a variety of the calculation of active or passive circuit for linear or nonlinear,but also obtain a wide variety of data,and then it is impossible for the Thevenin/Norton’s theorem to do this.But the the Thevenin/Norton’s theorem is more suitable for actual measurement to simplify the circuit,it is more convenient than Kirchhoff’s Law.

node；loop；equivalent resistance；short circuit current；the open circuit voltage

2016-05-18

1007-2934(2016)05-0022-04

TM 11

A DOI：10.14139/j.cnki.cn22-1228.2016.005.006

*通讯联系人