基于激光波数扫描干涉曲面轮廓度测量

广东工业大学自动化学院 王书雨 白玉磊 韩 韬 周延周

基于激光波数扫描干涉曲面轮廓度测量

广东工业大学自动化学院 王书雨 白玉磊 韩 韬 周延周

激光波数扫描干涉是一种新型激光干涉测量方法，具有稳定性好、测量精度高等优点。为了提高测量的精度，采用基于迈克尔逊干涉仪的波数扫描干涉的方法，并且对激光波数扫描干涉进行了理论分析和实验验证。并且运用矩阵的特征值分解与最小二乘法相结合的方法（EDLSA）对数据进行解调。此方法是一种广义的傅里叶变换，采用盲信号处理方式，不需要一些先验知识；并且通过和2D傅里叶变换的方法进行比较，证明此方法是可行的；并且EDLSA的测量精度16.86nm，而傅里叶变换的测量精度18.17nm。

激光波数扫描；傅里叶变换；特征值分解；最小二乘法

1.引言

激光测量是一种测量精度高、测量速度快、非接触性的测量方法［1-4］。目前，在测量物体的表面主要是针对具有漫反射性质的物体，而难以有效地测量具有镜面反射的物体。目前在测量具有镜面反射的材料一般采用两种办法：（1）采用坐标测量机等接触式测量，测量的速度较慢；（2）喷涂表面，改变其反射特性为漫反射后用光学方法测量。机械测量方法由于具有很多的局限性，所以很难在工业现场中进行使用；喷涂表面法尽管可改变物体表面的反射特性，但在很多场合下不能甚至无法进行物体表面喷涂。

目前，激光干涉测量检测手段在材料检测当中得到了广泛使用。1990年，相移干涉测量技术（PSI）被运用在测量物体表面的离面与面内位移上［5］；而该技术具有调制方便，结构简单，高精度等优点，其缺点是测量的时候容易受到外界扰动而引起误差［9］。电子散斑干涉测量技术（ESPI）是利用干涉的方法测量散斑干涉信号的相位变化来测量粗糙表面材料的形变［6］。2004年，英国拉夫堡大学J.M.Huntley小组提出波数扫描干涉技术（WSI）测量物体内部位移场分布，WSI利用半导体激光器的波长可调性质，对被测样件进行波长干涉扫描后，提取干涉光强序列的相位信息，测量出被测样件的微小位移量，该方法可对被测样品进行全场测量，系统抗干扰能力强［7］。2012年，英国拉夫堡大学的P.R.Ruiz等人使用激光波数扫描的方法测量内部混有少量微米级TiO2的树脂基复合材料构件内部的位移场分布［8］。2013年，广东工业大学提出了波数扫描方法测量三维位移场分布［9］，在此研究的基础上，本文提出矩阵特征值分解与最小二乘法结合的算法实现对镜面曲面的轮廓度的测量，我们称此算法为EDLSA算法。

2.镜面曲面轮廓度测量系统的构成

本实验系统是采用基于迈克尔逊干涉光路的激光波数扫描干涉测量原理，如图1所示。它由半导体激光器、CCD相机、分光棱镜、玻璃光楔、以及被测件组成。其中CCD相机采用维视MVVS142FM相机；激光是采用波长调制范围可达1.5nm的DFB半导体激光器，并且具有温度调节控制器，实现激光波长调制；光楔厚度为6.003mm，倾角为6′。

图1　镜面曲面轮廓度测量系统结构

LD：半导体激光器；TCM：激光器装置夹；L：准直透镜；CBS：分光棱镜；OW：光楔；CCD：相机；Sample：被测件表面；PC：计算机。

测量系统工作原理：如图1所示，当激光控制器输出的激光束经过准直镜后，由正方体分光镜CBS将其分为两束光。一束照射在光楔OW上，并在光楔前后面S1和S2产生反射，另一束光照射在被测件上产生反射。参考光楔与被测件表面反射的光分别经过正方体分光棱镜CBS反射和透射后并束，在CCD相机的像平面上形成干涉图像。图1中激光控制器LD的工作温度随时间变化，从30℃降到20℃，温度调制激光器输出波长，进行波数扫描，同时CCD相机采集600张干涉图像，计算机每张图像的每个像素点沿时间轴提取干涉光强序列，再进行数据处。

3.测量原理

3.1基于傅里叶变换的激光波数扫描原理

当激光控制器调制温度变化时，可使半导体激光器（DFB）的输出激光波数调制在一定范围。在波数扫描过程中，CCD相机拍摄干涉图像光强I与波数k扫描序列的关系为I（x，y，k），则CCD相机采集到的表面时间序列干涉光强为：

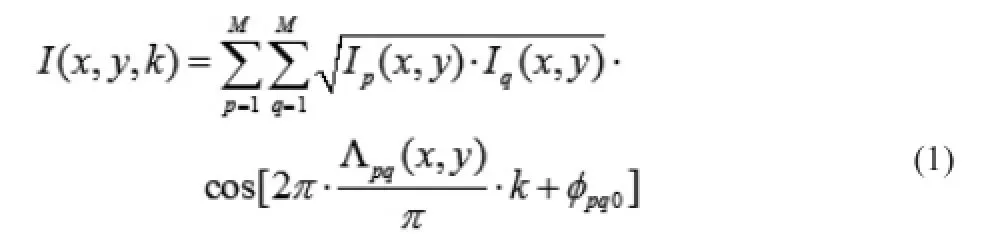
其中x，y为空间坐标；M为反射面的数量，此处为3；Ip、Iq分别表示p、q面反射光光强；p、q分别表示深度方向上p和q表面；Λpq（x，y）表示p和q表面之间的光程差，φpq0表示p和q表面之间的初始相位。对光强序列公式（1）进行傅里叶变换可得到：

3.2基于特征值分解与最小二乘法的测量原理

在波数扫描过程中，CCD相机拍摄干涉图像光强I与波数k扫描序列的干涉光强序公式（3）可表示为矩阵Q的形式：

其中矩阵A的大小为NS×M●（M-1），符号T为矩阵的转置，H为共轭转置矩阵，Δk为波数扫描范围，IP（p=1，2，…M）为反射面的反射光强，fpq和φpq（p=1，2，…M-1；q=p+1）分别表示干涉光强的频率和相位（fpq=Λpq/π；φpq=φpq0+2Λpqk（1）），φpq0为初始相位。矩阵Q为干涉光强，矩阵A和W包含频率fpq和相位φpq信息。矩阵W的高斯噪声矩阵均值μ=0；方差为σ2。

在上式中矩阵A可表示为A=［α1，α2，…，αns，…，α1，αNs］H，其中α是行向量。在这里我们定义干涉光强序列I（1），I（2），…，I（NS-1）为Q1；干涉光强I（1），I（2），…，I（NS-1），I（NS）定义为Q2；矩阵RQ1Q2为矩阵Q1自相关矩阵，矩阵RQ1Q2为矩阵Q1和Q2的互相关矩阵。

其中对角矩阵的大小为M●（M-1）×M●

（M-1），Δk为波数扫描范围。矩阵CQ1Q2和CQ1Q2的广义非零特征值分别为：ηpq和ζpq，而：

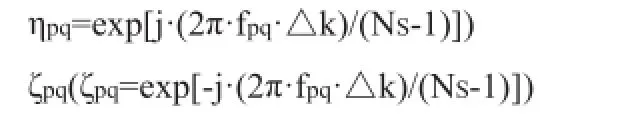
因此干涉频率fpq可以表示为：

若我们求得干涉的频率fpq，我们就可以计算出矩阵A。利用线性复数最小二乘法评估计算得矩阵G：

如果g1，g2，g1…，g（M·M-1）是矩阵G的元素，忽略负相，则在频域的干涉峰值卷绕相位可表示为：

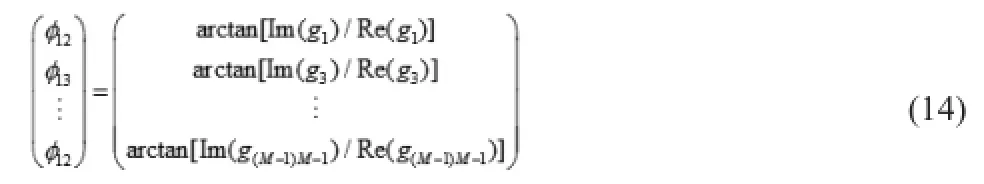
其中Im（）代表虚部，Re（）代表的是实部。再进行解卷绕处理，即可得出解卷绕相位。

4.测量结果

实验被测样品是具有镜面反射的材料，且只测量其中一块矩形区域，如图2所示：

图2　被测物体：苹果的LOGO（测量矩形区域）

对所拍摄到的干涉图的每一个像素点时间序列光强做傅里叶变换后，在每个像素对应被测表面与光楔后表面干涉信号的幅频峰值处提取相位，得到全视场卷绕相位；然后再对拍摄到的数据进行EDLSA算法处理，得到被测表面与光楔后表面的全场卷绕相位，再分别对这两组数据进行空间解卷绕运算，得到所拍摄镜面曲面的相位分布，如图4，图5所示：

图4　傅里叶变换的解卷绕相位

图5　特征值分解与最小二乘法的解卷绕相位

此时再分别对两组数据的相位，根据公式（6）求出三维轮廓信息。其中本文测量系统的激光器工作的中心波长λc=7.6×10-7m。分别对两组数据与标准的镜面曲面做差，得到被测件的镜面曲面的三维轮廓图，如图6，图7所示。从这两幅图中可以看出苹果LOGO表面的局部3维轮廓为一个起伏曲面，而起伏达差值达到±96nm。

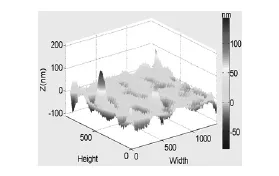
图6　傅里叶变换得到的曲面轮廓

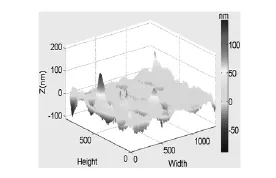
图7　EDLSA得到的曲面轮廓

在镜面加工，去除材料方式加工镜面表面粗超度Ra一般在0.8～0.08μm之间；无切削方式滚压（采用镜面工具）加工镜面粗超度Ra一般在0.4～0.05μm之间。本文测量材料粗超度Ra在0.8～0.08μm之间。而此时的测量镜面曲面的轮廓在0.2μm左右，在加工精度范围之内，测量是符合要求的。

再根据标准差公式（17），分别计算出被测表面的轮廓精度，傅里叶变换的测量精度为18.17nm，EDLSA的测量精度为16.86nm。

由以上数据分析可以看出EDLSA在测量镜面曲面轮廓度是可行的。

其中，s为被测物体表面的轮廓测量精度，m和n为CCD相机视场的大小，E为局部轮廓的测量误差值，m为局部轮廓测量误差的平均值。

5.结论

本文利用迈克尔逊干涉仪和半导体激光器波数扫描的方法，高精度测量镜面曲面的轮廓度。并且利用一种测量镜面曲面轮廓度的新算法：矩阵特征值分解与最小二乘法结合（EDLSA）算法。运用EDLSA算法提取出镜面曲面的相位轮廓，与2维傅里叶变换进行比较证明此方法的可行性，并且EDLSA算法的测量精度达到16.86nm，而傅里叶变换的测量精度18.17nm。并且EDLSA算法可以认为它是一种广义的傅里叶变换，它不仅具有傅里叶变换的所有优点，还可以自动评估计算提取相位峰值。EDLSA算法处理数据是一种盲信号处理方式，不需要一些先验知识。因此，此方法可以应用在镜面曲面轮廓度的测量上。

本文创新点：本文提出一种基于半导体激光器波数扫描干涉，高精度测量物体曲面轮廓的方法。运用矩阵特征值分解与最小二乘法结合（EDLSA）算法使得在测量曲面轮廓更加快。这种算法是一种广义傅里叶变换方法，不仅它不仅具有傅里叶变换的所有优点，还可以自动评估计算提取相位峰值，不需要一些先验知识。并且系统结构简单、稳定可靠、测量精度高，适合于机械零件的质量检验。

［1］苏显渝，谭松新，向立群等.基于傅里叶变换轮廓术方法的复杂物体三维面形测量［J］.光学学报，1998，18（9）：1228-1233.

［2］何艳敏，谢创亮，许卓明，鲍鸿，叶双莉，周延周.基于波数扫描干涉的表面轮廓测量［J］.激光技术，2016，40（3）：392-396.

［3］岳慧敏，苏显渝，李泽仁.基于复合光栅投影的快速傅里叶变换轮廓术［J］.光学学报，2005，25（6）：767-771.

［4］姜涛，习俊通，严隽琪.反求工程中融合特征捕捉的光学三维测量方法［J］.光电工程，2005，32（2）：19-22.

［5］P.K.Rastogi.Digital speckle pattern interferometry and related techniques［M］.United Kingdom：John Wiley & Sons Ltd，2001.

［6］Y.Zhou，R.D.Wildman，J.M.Huntley.Measurement of the mechanical properties of granular packs by wavelength scanning interferometry ［J］.Philos.T.R.Soc.A，2010：466（3）：789-808.

［7］Pablo D Ruiz，Jonathan M Huntley，et al..Depth-resolved wholefield displacement measurement by wavelength-scanning electronic speckle pattern interferometry［J］.Applied Optics，2004（6）：679-683.

［8］S.Chakraborty，P.D.Ruiz，Measurement of all orthogonal components of displacement in the volume of scattering materials using wavelength scanning interferometry［J］.Opt.Soc.Am.A，2012，29（9）：1776-1785.

［9］J.Xu，Y.Liu，B.Dong，et al.Improvement of the depth-resolution in the depth-resolved wavenumber-sca nning interferometry using multiple uncorrelated wave-number bands［J］.Appl.Opt.，2013，52（20）：4890-4897.

周延周【通讯作者】（1964—），吉林人，博士，教授，主要研究方向：3D机器视觉测量。

王书雨（1990—），男，硕士，现就读于广东工业大学。