面向三轴气浮台的室内星敏感器定姿方法
2016-11-17孙兆伟
肖 岩,叶 东,孙兆伟
(哈尔滨工业大学 航天学院,哈尔滨 150001)
面向三轴气浮台的室内星敏感器定姿方法
肖 岩,叶 东,孙兆伟
(哈尔滨工业大学 航天学院,哈尔滨 150001)
为解决三轴气浮台垂直于地面转轴转角(偏航轴转角)难以精确测量的问题,提出了使用室内星敏感器进行三轴姿态角测量的方法.考虑到室内星敏感器与在轨星敏感器工作环境的区别,基于在轨星敏感器姿态测量方法对室内星敏感器姿态测量方法进行了研究与改进.在建立室内星敏感器姿态测量模型的基础上,采用迭代算法寻优得到三轴台高精度的三轴姿态.针对迭代算法对初始值要求较为严格的情况,采用粒子群优化算法寻优得到初始姿态矩阵.数学仿真结果验证了室内星敏感器测姿方法能够在快速测量3个转轴转角的基础上,提高偏航轴转角的精度.
室内星敏感器;三轴气浮台;姿态测定;粒子群优化;迭代
使用气浮台来进行飞行器的地面仿真始于21世纪50年代,当时美国和苏联开始了包括人造卫星、载人航天和月球探测等一系列项目在内的太空竞赛[1].气浮平台转动或者平移时极小的摩擦特性可以高度模拟太空中的微重力环境,这种仿真模式的最大优势在于可以大幅度降低太空科学任务的风险.进入21世纪中国的航天任务逐渐增多,为保证每次任务的可靠性,使用气浮台进行地面仿真已成为一种必不可少的仿真手段.现代化的三轴气浮台可以仿真卫星多项在轨功能,如在轨实时数据传输,在轨姿态确定和在轨姿态控制等.姿态确定利用星上的敏感器测量得到的信息,经过适当的处理,求得固联于卫星本体的体坐标系关于空间某惯性参考系的姿态,是多项在轨任务实施的前提.基于三轴气浮台的姿态半物理仿真不仅使得科研人员可以近距离观察研究飞行器姿态机动的动力学和控制问题,而且由于半物理仿真使得一些在轨任务以硬件的物理方式参与了仿真过程,使得试验结果更加完善、真实可信.
当前的气浮台姿态敏感系统主要包括惯性测量单元、三轴微机电陀螺仪和双轴倾角仪,例如文献[2]提出的采用“MEMS陀螺+倾角传感器”的方法,并且以此为中心建立了三轴气浮台姿态确定系统;北京控制工程研究所提出的采用“机械陀螺+加速度计+倾角传感器”的方案.由于偏航角的变化并不能引起静态重力加速度的变化,所以不能由精度更高的倾角仪去测量,一般只能由精度较低的磁强计去测量,由于磁强计较倾角传感器精度差很多,所以现有的姿态测量系统不能提供足够精确的偏航轴姿态角以及角速度,新的测量方法亟待开发.针对这一问题,佐治亚理工大学和美国海军研究学院[3-4]提出了使用磁强计、太阳敏感器和速率陀螺来测量气浮台姿态的方法,但这一方案尚有不足之处:磁强计很容易受到其他干扰源的干扰,例如电脑、手机、空调电路和其他一些设备中的永磁体等;对于太阳敏感器来说,不方便之处是需要建立一个相应的太阳模拟器来模拟太阳;倾角仪只能测出关于水平面偏转的两轴倾角,速率陀螺仪可以测出三轴的角速度信息,但是高精度的速率陀螺仪和倾角仪较为昂贵[5].本文考虑到目前国内外卫星上普遍使用星敏感器或“星敏感器+惯性原件(陀螺)”的组合来进行卫星在轨姿态的确定这一情况,针对该问题提出了一种能在实验室条件下使用室内星敏感器精确测量三轴气浮台姿态的方法.室内星敏感器主要组成部件为CCD相机和微处理器,这两个组成部件价格便宜,工作原理简单,而且星敏感器姿态测量精度远远高于陀螺、倾角仪和磁强计[6].使用星敏感器进行三轴台的姿态测量不仅可以使姿态半物理仿真更接近在轨卫星的姿态测量过程,而且还可以充分利用星敏感器姿态测量的优势[7].在研究过程中发现,由于实验室环境与真实太空环境的差异,室内星敏感器无法用角度这一重要特征来进行星图识别,目前国内外还没有专门针对这一问题的研究.
本文针对上述问题,提出了结合迭代算法与粒子群寻优算法的室内星敏感器姿态测量方法,首先,建立基于室内星敏感器的三轴转台的姿态测量模型;其次,给出姿态测量迭代算法,进行星点识别中的角度对比;然后,引入粒子群优化算法进行初始姿态寻优估计;最后,进行数值仿真,验证姿态测量方法的有效性.
1 室内星敏感器姿态测量
室内星敏感器主要由CCD相机和微处理器组成,其工作原理与星敏感器相似,主要步骤如下[8].
Step 1 星图拍摄.首先由CCD相机对悬挂于实验室顶部的液晶显示器(模拟星空)进行星图拍摄.
Step 2 星点提取.星点提取主要是从星图照片中得到星点在像平面的位置坐标,进而得到星点在星敏感器坐标系中的位置矢量.
Step 3 星图识别.星图识别是识别拍摄星图中的星点在参考坐标系中对应的恒星,进而可以获得该星点在参考坐标系中的位置矢量,此过程需要导航星表,导航星表主要是星点在参考坐标系中的位置信息[9].主要方法有角度识别法和三角形识别法等[10].
Step 4 姿态计算.姿态计算是综合星点在星敏感器坐标系和参考坐标系中的位置信息来得到飞行器关于参考坐标系的姿态.主要方法有最小二乘法、四元数估计法、TRIAD等[10].
实验室仿真使用LED屏来模拟星空,LED屏上星点的位置由MATLAB随机生成,本文直接使用MATLAB产生的随机坐标矩阵来表示星点在LED屏上的位置信息.CCD相机固定置于三轴转台顶部,三轴转台的转动即是在轨飞行器的姿态机动.导航星表信息是三轴转台姿态角为0°时,由CCD相机拍摄的星图信息建立.
为后续建立测量模型的需要,建立室内星敏感器姿态测量数学模型.首先建立描述姿态关系的坐标系,如图1所示.设I是原点位于转台中心的参考惯性系,I′是I坐标系的原点从转台中心转移到CCD相机中心后的转移参考坐标系,其中I为静坐标系,I′为动坐标系.B坐标系是固联在CCD相机上的体坐标系,B′坐标系是原点位于转台中心,3个坐标轴始终与B坐标系保持相同的转移相机体坐标系,两个坐标系均随三轴转台旋转,是动坐标系.当三轴转台姿态角为0°时,B′坐标系与I坐标系重合,转移向量R0从转台中心指向CCD相机,且固联于转台体坐标系.h为LED屏到转台中心的距离,h1为LED屏到CCD相机的距离.

图1 室内星敏感器姿态测量模型
三轴转台的姿态用B′坐标系与I坐标系之间的转换矩阵来表示.本文使用TRIAD方法确定三轴转台的姿态[11].假设被正确识别的两颗恒星为S1和S2,其在卫星体坐标系中的星矢量为b1和b2,在参考坐标系中对应的星矢量为r1和r2.图2中S坐标系为原点处于投影中心的像空间坐标系,即固联在CCD相机上的B坐标系,S0坐标系为表示CCD靶面的焦平面坐标系.根据焦面星图中的星点坐标计算单位星矢量b1和b2的方法如下:
式中:Xc、Yc分别为星点在焦面星图中的坐标;f为相机焦距.参考坐标系中的星矢量r1和r2可以通过导航星表得到.
A为方向矩阵,满足矩阵运算:
Ar1=b1,Ar2=b2.
令
所以有
建立参考矩阵与观测矩阵:
那么方向余弦矩阵可求得:


图2 CCD相机测量模型
星敏感器的姿态测量精度很高,但是室内星敏感器不能直接使用星敏感器的姿态测量方法,因为室内星敏感器的CCD相机不能置于三轴转台中心,所以室内星敏感器体坐标系对于惯性参考坐标系(原点固定在三轴转台中心)不仅有旋转,还有平移.在轨任务中,由于星体距地球和飞行器很远,CCD相机与飞行器本体之间的平移带来的影响可以忽略.在实验室中,LED屏距离CCD相机只有2 m左右,坐标系之间的平移不能忽略.当转台转动时,CCD相机视场中星点的相对位置会发生变形,在用角度识别法进行星图识别时,由图1可知,观测星矢量b1和b2之间的夹角与参考星矢量r1和r2之间的夹角并不相等,而是与三轴转台的姿态相耦合.所以在星图识别的过程中把b1和b2之间的夹角当作r1和r2之间的夹角,和星库中的夹角数据进行比较,识别所选定的星点,会产生很大误差.
除了角度识别算法,其他几种常用的星图识别算法如面三角识别算法[12]和球面三角识别算法[13]均要用到星矢量之间的夹角这一特征信息,所以这一问题使得许多星图识别算法不能正常使用,需要进一步改进.
2 姿态迭代算法
定义αi为第i颗星到B坐标系原点的距离,定义βi为第i颗星到I坐标系原点的距离,满足如下几何关系:
在B坐标系中表示为
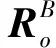
假设室内星敏感器相机朝向沿-zB轴,设向量pI′=[0,0,-1]T,从LED屏到I坐标系原点的距离h已知,那么αi满足下式:

所以解得
同理
导航星库中的星矢量、角度和面积等信息是在三轴转台姿态角相对于参考惯性系为0时,将B坐标系中的星矢量转换到I坐标系中得到的,其中
因为αi是姿态矩阵A的函数,不能直接求出姿态矩阵A,可以利用姿态计算方法结合迭代思想达到求得姿态矩阵的目的.
Step1 对姿态矩阵进行预测. 提供初始的姿态矩阵A0,A0可由转台上搭载的其他敏感器提供,也可以使用前一时刻得到的姿态信息.



Step 6 以A1为新的姿态估计继续Step 2,直到算出的姿态矩阵Ai达到精度要求.
3 基于粒子群算法的姿态寻优
在对姿态迭代算法进行仿真时发现,姿态迭代算法使用的前提是初始的姿态估计矩阵A0具有较高的精度,如果A0误差较大,迭代算法就无法输出符合精度要求的姿态信息.
实际在轨任务中,有时星敏感器无法提供初始姿态信息,或者初始姿态信息不完整,此时就需要进行初始姿态的识别.在实验室条件下,在没有任何初始姿态信息或者初始姿态信息不完整的情况下,可以运用姿态寻优的方法获得精度较高的初始姿态信息.
进行寻优的算法有很多种,如遗传算法、最速下降法、拟牛顿法、粒子群算法、差分进化算法等其他算法[14].设识别星点数为目标函数,考虑到目标函数的不连续和不可导[15],以及星图识别和姿态计算方法的特殊性,本文选用粒子群算法进行寻优.
粒子群算法初衷是通过模仿动物社会个体之间的交往来产生一种有智能的计算方法.粒子群算法的输入—粒子,将会被置于待优化问题的解空间中,然后将有一个与目标函数有关的适应值函数来评价粒子此时位置的适应值.每个粒子通过结合自己位置的最优适应值和整个粒子群体的最优适应值这两方面的信息,以及其他一些随机刺激来决定自己在解空间中的运动方向,进而更新自己的位置.当所有的粒子都更新完自己的位置后,再进行新的一次迭代.经过多次迭代后,粒子群就渐渐集中到最优位置附近[16],此时粒子所载有的信息就是最优解.
粒子群优化的算法流程如下:
1)初始化一群粒子(粒子数为m),包括每个粒子随机的位置和速度;
2)评价每个粒子的适应度;
3)对每个粒子,将它的适应值和粒子自己的历史最优位置pi的适应值pbest(改为下标形式)作比较,如果较好,则将其作为当前的最好位置pi;
4)对每个微粒,将它的适应值和全局历史最优位置pg的适应值gbest作比较,如果较好,则将其作为当前全局历史最优位置pg;
5)在粒子群算法中,每次迭代不仅要更新粒子位置xi,还要调整粒子速度vi,所以粒子会在pi和pg位置周围随机震荡,并且逐渐靠近.其中每个粒子的位置和速度更新为
6)如达到结束条件(通常为达到预设误差或足够好的适应值或达到一个预设最大代数Gmax),则退出,否则回到流程2).
以下进行初始姿态寻优建模.
设粒子数为M,i粒子的位置为一个三轴旋转角输入,旋转顺序为x-y-z.
粒子i的三轴输入角变化速度表示为
粒子i的局部最佳输入三轴旋转角表示为
整个粒子群的全局最佳输入三轴旋转角表示为
待优化问题就是飞行器的三轴姿态,其中每一个粒子输入,运行一遍星图识别算法,用其输入的三轴姿态角计算识别星点数N,并把识别星点数的相反数-N作为粒子的适应值F.所以识别星点数越多,粒子的适应值就越小,粒子输入的三轴姿态也就越接近气浮台的三轴姿态.当寻优使得适应值函数达到最小值时,此时的粒子三轴信息就是当前三轴转台的三轴姿态.需要说明的是,选取识别星点数作为适应值不仅可以准确反映姿态输出的精确程度,而且在星点数较多时,可以减少粒子群算法运行的计算量,缩短收敛时间,与用输出姿态信息计算姿态精度相比,更加简单直观.
粒子群算法在寻优过程中有5个寻优参数,分别是惯性权重w,加速因子c1、c2,随机常数r1、r2(均匀分布在0~1之间).此外还有两个限制参数:最大速度vmax和最大迭代次数Gmax.每个参数的变化都会影响算法的收敛性和收敛速度[17].考虑到实验条件以及室内星敏感器姿态测量方式,经过多次程序运行调试,选取收敛性较好的参数设置如下:
在实际的在轨飞行任务中,有些姿态控制操作是实时的,因此需要姿态信息的测定也是接近实时的,而姿态寻优的过程有一定的时间消耗,如果星点数较多,耗费的时间会更多,基本丧失了实时性.迭代算法虽然实时性要优于姿态寻优,但是对初始姿态信息有一定的精度要求.考虑到这两种方法的特点,将姿态寻优与姿态迭代相结合来进行姿态测量,主要步骤如下.
Step 1 使用粒子群算法进行初始姿态角寻优,得到满足迭代算法精度要求的初始姿态估计矩阵A0.
Step 2 使用Step 1得到的初始姿态估计矩阵A0进行姿态迭代,得到三轴转台的姿态更新矩阵A1.
Step 3 令A0=A1,重复Step 2,直到迭代计算的姿态矩阵Ai满足精度要求,此时输出Ai作为三轴转台此时的姿态矩阵.
4 仿真实验
硬件基本参数设定如下:三轴转台中心到LED屏的距离h为2 000mm;CCD相机到LED屏的距离h1为1 800mm;LED屏幕为边长1 200mm的正方形.仿真计算机基本性能参数:CPU为Intel酷睿2双核T7700(2.4GHz);内存为DDRII(1GB);硬盘为SATA(160GB).
姿态迭代算法的本质是将星敏感器前一时刻的姿态信息或者其他精度较低的敏感器的姿态信息融合到室内星敏感器的姿态测量过程中来.迭代算法的仿真除了要看其姿态输出结果,还要分析迭代算法对初始姿态估计的要求.仿真过程中星位置点用MATLAB随机矩阵来表示,所以仿真结果中不包含星点提取误差.
为了使姿态迭代算法得到符合条件的姿态测量值,首先仿真分析姿态迭代算法对姿态预测初始值A0的精度要求;然后仿真分析姿态迭代次数对姿态测量精度的影响.
仿真内容及结果如下:
1)三轴转台姿态角为0°,设置A0的误差为0°、3°、6°、-3°、-6°,分别进行姿态计算,星图识别使用角度识别法,姿态计算使用TRIAD算法,仿真结果见表1.

表1 A0误差对星点识别的影响 (°)
2)在A0误差是-2°的情况下,迭代次数从1次增加到5次,观察识别星点数的变化,仿真结果见表2.
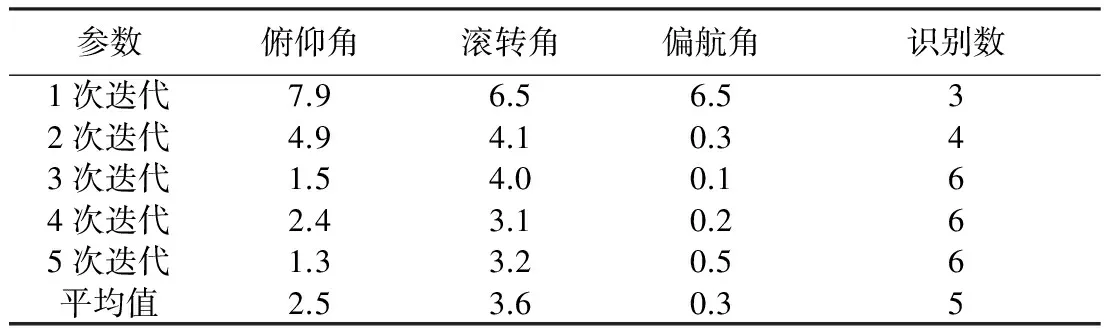
表2 A0误差是-2°时迭代仿真数据 (10-3(°))
初始姿态矩阵A0的误差对姿态测定的结果影响较大,当误差达到±3°时,识别星点数下降较为明显.当误差达到±6°时,姿态测定就无法进行了.在初始矩阵A0误差不是很大的情况下,增加迭代次数可以有效地提高星点识别的个数,从而提高姿态测量的精度.
需要说明的是,表2中设置平均值是为了更方便地体现随着迭代次数增加,姿态角测量值更接近目标值的趋势.因为在仿真过程中发现,有时姿态角在经过2~3次迭代后就很接近目标值,之后的迭代并不能使其更接近目标值,只是在目标值附近很小的范围内波动,趋于稳定,但整体的趋势是随着迭代次数增加,姿态角测量值逐渐接近设定值,且识别星点数逐渐增加.另外,在计算平均值的过程中剔除了误差较大的第1次迭代后的姿态数据,这样计算得出的平均值能更准确体现姿态测量过程中迭代法的迭代效果.
用仿真分析粒子群寻优算法与迭代法结合的姿态测量效果.设星点数为50,粒子数为5,三轴转台滚转角、俯仰角和偏航角初始值分别为2°、3°和0.5°,在0~40 s时间内,三轴转台保持现有的姿态静止不动.从40 s开始,三轴转台开始转动,三轴角速度依次为0.05、0.10、0.01°/s,持续变化100 s,三轴姿态输出和真实姿态在140 s内的对比如图3~5所示.
分析3个欧拉角的对比图可知,采用粒子群算法进行姿态寻优可以得到符合迭代法精度要求的初始姿态矩阵.由于粒子群算法寻优的误差保持在一个数量级,所以当某一个坐标轴转过的角度较小,如图5的初始偏航角为0.5°,在寻优的绝对误差保持在一个数量级的情况下,寻优的相对误差就会较大.这个情况可以从图3~图5在40 s时的角度对比可以看出,滚转角和俯仰角由于初始角度较大,所以寻优的相对误差较小,而偏航角相对较小,所以寻优的相对误差较大.寻优相对误差较小的前两个角,迭代法在较短时间内就可以得出精度较高的姿态输出;寻优相对误差较大的偏航角,迭代法用了相对较长的时间得到了精度较高的姿态输出,但都在可接受的范围之内.
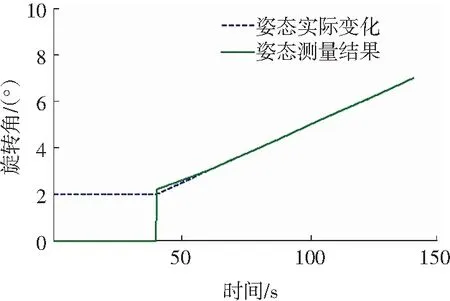
图3 滚转角姿态寻优对比

图4 俯仰角姿态寻优对比

图5 偏航角寻优对比
5 结 论
1)迭代算法在星图识别过程中,引入前一时刻的姿态信息,解决了在实验室环境下,观测星矢量夹角和参考星矢量夹角不能直接比较识别的问题.
2)使用粒子群优化算法得出的初始姿态估计矩阵满足迭代算法进行角度识别时对初始姿态精度的要求.
3)结合迭代算法和粒子群优化算法的室内星敏感器可以测得偏航轴转角,并且其精度基本接近俯仰轴转角和滚转轴转角.
[1] 帕迪利亚. 科学探索者天文学[M]. 浙江: 浙江教育出版社, 2002: 98.
[2] 陈茂胜,金光,徐开,等. 微型三轴气浮台姿态确定系统设计[J]. 系统仿真学报, 2012, 24(10): 2102-2107.
CHEN Maosheng, JIN Guang, XU Kai, et al. Design of micro tri-axial air turntable’s attitude determination system[J]. Journal of System Simulation, 2012,24(10):2102-2107.
[3] 戴路, 金光, 陈涛. 基于VSCMG 的卫星姿态控制仿真系统[J]. 光学精密工程, 2008, 16(8): 1546-1552. DOI:10.3321/j.issn:1004-924X.2008.08.033.
DAI Lu, JIN Guang, CHEN Tao. Satellite attitude control simulation test bed based on VSCMG[J]. Optics and Precision Engineering, 2008, 16(8): 1546-1552. DOI:10.3321/j.issn:1004-924X.2008.08.033.
[4] 蒙涛, 王昊, 金仲和, 等. 基于低成本MEMS 传感器的皮卫星融合定姿算法研究[J]. 宇航学报, 2009, 30(4): 1569-1572. DOI:10.3873/j.issn.1000-1328.2009.04.043.
Meng Tao, WANG Hao, JIN Zhonghe, et al. A Fusion algorithm for pico-satellite attitude determination using low cost mems-based sensors[J].Journal of Astronautics, 2009, 30(4):1569-1572.DOI:10.3873/j.issn.1000-1328.2009.04.043.
[5] 朱长征. 基于星敏感器的星模式识别算法及空间飞行器姿态确定技术研究[D]. 长沙: 国防科学技术大学, 2004.
[6] 贾辉. 高精度星敏感器星点提取与星图识别研究[D]. 长沙: 国防科学技术大学, 2010.
JIA Hui. Star centroid estimation and star identification of high accuracy star tracker[D]. Chashang: National University of Defense Technology, 2010.
[7] 刘一武,陈义庆.星敏感器测量模型及其在卫星姿态确定系统中的应用[J].宇航学报, 2003,24(2):162-165. DOI: 10.3321/j.issn:1000-1328.2003.02.009.
LIU Yiwu, CHEN Yiqing. Star-sensormeasurementmodel and its application to the spacecraft attitude determ ination system[J]. Journal ofAstronautics, 2003,24(2):162-165. DOI: 10.3321/j.issn:1000-1328.2003.02.009.
[8] LERNER G M. Three-Axis Attitude Determination[M]// WERTZ J R. Spacecraft Attitude Determination and Control. Berlin and New York: Springer, 1978: 420-488.
[9] 阚道宏,朱铮,过瑞英. 星敏感器用导航星星表的建立[J]. 宇航学报,1992,13(4):43 - 49.
KAN Daohong, ZHU Zheng, GUO Ruiying. Gulde star SUB-catalog generation for star sensor[J]. Journal of Astronautics, 1992,13(4):43- 49.
[10]LEE S H, AHN H S, YONG K L. Three-axis attitude determination using incomplete vector observations[J]. Acta Astronautica, 2009, 65(7-8):1089-1093. DOI:10.1016/j.actaastro.2009.03.018.
[11]SHUSTER M D, OH S D. Three-axis attitude determination from vector observations[J]. Journal of Guidance and Control, 1981, 4(1): 70-77. DOI: 10.2514/3.19717
[12]COLE C L, CRASSIDIS J L. Fast star-pattern recognition using planar triangles[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(1): 64-71.DOI: 10.2514/1.13314.
[13]WU Yunhua, GAO Yang, LIN Jiawei, et al. Low-cost, high-performance monocular vision system for air bearing table attitude determination[J]. Journal of Spacecraft and rockets, 2014, 51(1):66-75.DOI: 10.2514/1.A32465.
[14]LIEBE C C. Star trackers for attitude determination[J]. IEEE Aerospace and Electronic Systems Magazine, 1995, 10(6): 10-16. DOI: 10.1109/62.387971.
[15]罗辞勇, 陈民铀. 适应性粒子寻优算法[J]. 控制与决策,2008,23(10):1135-1138.
LUO Ciyong, CHEN Minyou. Adaptive particle swarm optimization algorithm[J]. Control and Decision,2008,23(10):1135-1138.
[16]RATNAWEERA A, HALGAMUGE S K, WATSON H C. Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(3) : 240 -255. DOI: 10.1109/TEVC.2004.826071.
[17]ANGELINE P J. Using selection to improve particle swarm optimization[C]//Proceedings of the 1998 IEEE International Conference on Evolutionary Computation, ICEC’98. Piscataway, NJ: IEEE, 1998: 84-89.
(编辑 张 红)
The attitude estimation of the triaxial air bearing table based on an indoor star tracker
XIAO Yan, YE Dong, SUN Zhaowei
(School of Astronautics, Harbin Institute of Technology, Harbin 150001, China)
In order to measure the Euler angle of the axis perpendicular to the ground level (yaw axis) of the triaxial air bearing table, a new approach for attitude estimation using an indoor star tracker is proposed. Considering the difference of the working condition between the indoor star tracker and the star tracker on orbit, this study is to improve the indoor-star tracker attitude estimation. The iterative attitude algorithm is used in the attitude estimation model of the indoor-star tracker to achieve a higher precision attitude. Because the iterative attitude algorithm requires a good guess of initial altitude matrix, an attitude optimization using the particle swarm optimization is introduced to get the initial attitude matrix. The simulation results show that the improved attitude estimation based on an indoor-star tracker can improve the attitude estimation precision of the yaw axis when measuring all three Euler angles efficiently.
indoor star tracker; triaxial air bearing table; attitude estimation; particle swarm optimization; iterative method
10.11918/j.issn.0367-6234.2016.10.007
2015-03-23
中央高校基本科研业务费专项资金(HIT.NSRIF.2015033);微小型航天器技术国防重点学科实验室开放基金(HIT.KLOF.MST.201501);中国博士后科学基金(2015M81455);黑龙江省博士后基金(LBH-Z15085)
肖 岩(1990—),男,硕士;
孙兆伟(1963—),男,教授,博士生导师
叶 东,yed@hit.edu.cn
V448.25
A
0367-6234(2016)10-0051-06
