二维Kleinberg网络上疾病传播的最优局部控制策略

鲍中奎，张海峰

（安徽大学数学科学学院 合肥 230601）

二维Kleinberg网络上疾病传播的最优局部控制策略

鲍中奎，张海峰

（安徽大学数学科学学院 合肥 230601）

研究二维Kleinberg网络上的疾病传播及最优控制问题。基于Manhattan距离提出了一种局部的控制策略抑制疾病在Kleinberg网络上的传播，并进一步研究该策略对系统总的代价（定义为最终感染比例和治愈人数比例之和）的影响。通过研究发现，当Kleinberg网络中长程边数量和疾病传播率在一定范围内时，会存在一个最优控制半径，使系统代价最小。当控制半径小于最优控制半径，局部控制策略不能有效地抑制疾病的传播，导致很多节点被感染；当控制半径大于最优控制半径，虽然疾病的传播范围被有效地控制，但是会花费更多的代价用于控制疾病传播。并且最优控制半径会随着疾病的传播率以及刻画网络的参数改变而发生变化。

代价函数； 疾病传播； Kleinberg网络； 局部控制

通信网络中的病毒传播以及社会网络中的疾病传播都可以抽象为复杂网络上的传播动力学问题，因此对复杂网络上传播动力学行为的研究是复杂网络领域的一个重要命题［1-7］。研究疾病传播的根本目的是为了有效地预防、控制疾病的大范围扩散，减小疾病爆发带来的危害，因此学者们提出了多种免疫策略，如目标免疫［8］、熟人免疫［9］、基于随机游走的免疫策略［10］以及删边免疫策略等［11-12］。

已有的免疫策略虽然在某些条件下可以有效地控制疾病在网络上的传播，但是这些免疫策略存在以下共同问题：1） 这些免疫策略是在疾病还没有发生之前就实施，在现实情况中，很多突如其来的疾病往往缺乏及时、充分有效的疫苗，因此免疫或者治愈措施往往是发生在疾病爆发之后；2） 已有的免疫策略多关注能否最终控制疾病传播范围而忽视免疫或控制措施自身带来的成本代价问题；3） 已有的免疫策略都要求人们掌握网络的结构信息，而对于一个充分大的网络，要想获取网络的结构信息较为困难。因此需要更为合理的控制策略。

文献［13］提出了一种局部控制策略（类似于环状免疫策略）。在该模型中，假设感染者分为隐形感染者和显性感染者，隐性感染者以一定概率变为显性感染者。显性感染者以一定的概率恢复为恢复者，同时显性感染者也可以以一定的概率被治愈，并且将其周围一定半径内的所有个体也一并治愈（包含易感染者和感染者）。然后定义系统总的代价为恢复者和治愈人数之和，通过研究发现，对于一维和二维的Newman-Watts小世界网络（简称NW网络［14］），均存在一个最优的控制半径。

NW网络虽然可以部分地刻画现实网络中的小世界性——平均距离小、聚类系数大的特征［15］，但是对于网络上的长程边是随机加上去的，导致网络的可搜索性不够好；且NW网络是无向网络。基于以上原因，Kleinberg对二维的NW网络进行改进，提出了经典的Kleinberg网络模型。通过研究发现对于二维的Kleinberg网络，当网络规模趋向无穷大时，存在一个最优的参数α，使网络中任意两点之间的平均传递步数最小［16-17］。

基于以上原因，本文通过研究发现，当m和疾病的传播率在一定范围内时，二维Kleinberg网络上同样存在一个最优的控制半径，使系统总的代价最小；且该最优半径随着传播率的增加而增加，当传播率很大时，这种最优现象会消失。尤为重要的是，该最优现象随着α的增加变得更加明显。

1 二维Kleinberg模型

二维Kleinberg模型是对二维NW进行改进，具体如下［5，15-16］：

1） 从规则网络开始，首先构造一个具有周期边界条件的二维方格，每个节点和最近邻的4个邻居互为邻居，即假设每个节点和周边4个邻居的连边是双向边。

2） 偏好性加长程边，为了保证网络的小世界特性和可搜索性，定义每个节点都有m条“有向”的长程边指向网络中其他的m个节点（保证不重连）。不同于NW网络中的随机加边，要求每个节点i指向其他节点j的概率与这两个节点的Manhattan距离有关，具体定义如下［5］：

文献［15］指出当N→∞时，α=2是唯一的最优值，此时分散式算法所需的平均传递步数至多是log（N） 的多项式函数，即对于规模很大的网络，平均而言每个个体可以经过很短的步数，找到网络中需要搜索的目标节点。

2 疾病传播模型

在疾病传播部分，本文采用了改进的SIR模型［13］。它将包括几种状态：隐形感染状态（I）、显性感染状态（D）、恢复状态（R）、治愈状态（V）、易感状态（S）。隐形感染状态与显性感染状态的区别是后者可以被识别，且有可能激发局部控制策略，而前者因其隐形特征却不能被识别。疾病传播开始阶段，模型中随机初始化5个节点为I态，其他节点都为S态。一个S状态节点可以被其邻居中的I或D状态节点以概率p感染，成功感染后成为I状态。当一个I节点被诊断后，I状态节点以概率q成为D状态。一个D状态节点或以概率r恢复成R状态或以概率v引发局部控制策略。局部控制的范围是与此D状态节点的Manhattan距离小于或等于z的节点（S态节点或者I态节点）。既没变成R状态也没变成V状态的节点在下一步有可能恢复，也有可能再去感染其他节点。模型流程如图1所示［13］。

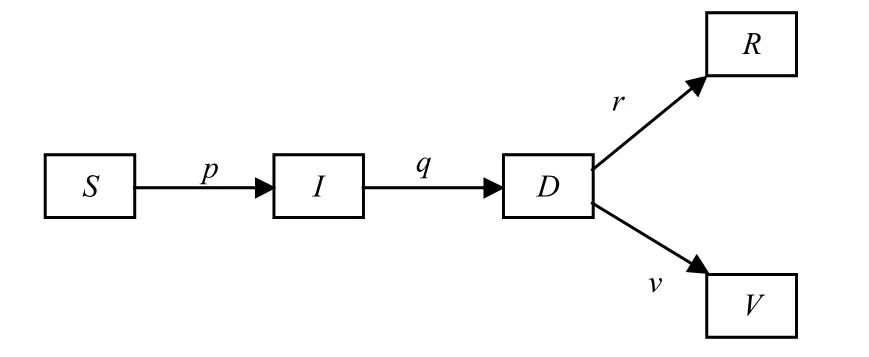
图1 在传播模型示意图

整个传播过程直到隐形感染状态与显性感染状态节点个数之和为零，即I（t）+D（t）=0时停止。

3 仿真及分析

本文在N=50×50的二维Kleinberg网络上进行了疾病传播过程，同时考虑了每个节点长程边数目m=1和m=2的情况。

首先引入一个代价函数X =V （∞） + R（∞），用来衡量疾病爆发所付出的代价。X表示在整个疾病传播过程中，最终导致染病个体（ R（∞） ）比例与治愈个体（V（∞） ）比例（治愈的代价）之和。

随机加有向长程边如图2a所示，更倾向连接距离近的节点如图2b～图2c所示。从图2可以发现，对于m=1和不同的传播率p，无论α=0或者α＞0，当z值小时，代价X偏高，而随着z到达最优控制半径z=zc，最优半径 随着传播率p的增加而增加。这

是因为随着传播p进一步增加，疾病更容易在网络上传播，此时需要控制更大范围的节点才能抑制疾病爆发。若进一步增加p会导致疾病在整个网络爆发，此时要么大范围控制疾病传播，即增加控制半径z；要么完全不控制，这两种情形都会导致系统总的代价趋于1，因此最优半径现象会逐渐消失。

通过比较图2a～图2d可以发现，随着α的增加，最优现象变得更加明显，即X刚开始随着z的增加下降更快，然后又随着z的增加上升更快。这种现象的原因在于：当α＞0时，长程边更倾向指向离自己近的节点，因此网络局域化效应更明显。在此情况下，一方面疾病不容易传播，另一方面，局部控制策略可以更有效地阻止疾病通过长程边向远处扩散。参数为m=1，q=0.5，r=0.1，v=0.1。

为了分析出现最优半径的原因，本文分别研究了最终传播比例R（∞）（如图3a所示）、治愈比例V（∞）（如图3b所示）及总代价X（如图3c所示）与z的关系。从图3可以发现，随着z的增加，最终传播比例R（∞）快速下降，导致治愈比例V（∞）也相应降低，因此总的代价X达到一个最小值。从图3a～图3b可以发现，随着进一步增加控制半径z，传播比例 R（∞）→ 0，再增加z只会导致更多的人被治愈，即V（∞）增加，最终导致系统总的代价X增加。参数为m=1，q=0.5，p=0.08，r=0.1，v=0.1。

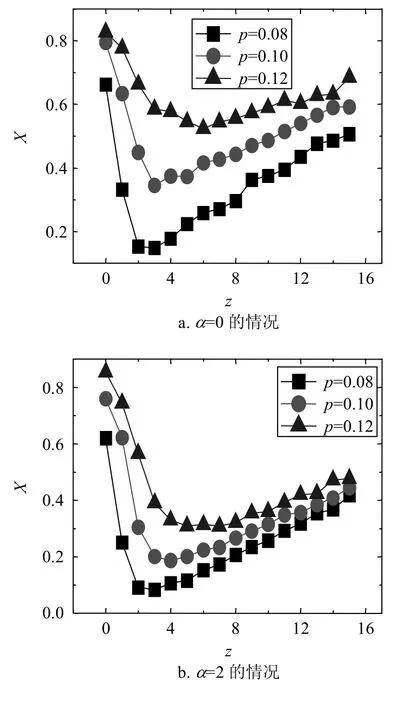
图2 在不同参数α以及传播率p的情况下，总的代价X（X=R（∞）+V（∞）与局部控制半径z的关系

图3 对于不同参数α，控制半径z对最终传播比例、治愈比例以及总的代价的影响

图4所示为代价函数X与控制半径z以及参数α的关系，参数为m=1，q=0.5，r=0.1，v=0.1。由图可以发现，随着α的增加，最优现象更加明显，同时总的代价函数X也变得越来越小。随着α的增加，个体更倾向指向距离近的邻居，使网络的局域化现象更加明显，导致一方面疾病不容易传播，另一方面局域控制策略更有效地控制疾病向远处传播。

图4 在p=0.1的情形下，总的代价X与参数α及局部控制半径z的关系

进一步研究m=2的情况，即每个节点有两条长程边指向远处节点。通过图5和图6可以观察到m=2的定性性质和m=1的完全一样。在图5中，参数m=1，q=0.5，r=0.1，v=0.1。在图6中，参数为m=2，q=0.5，r=0.1，v=0.1。

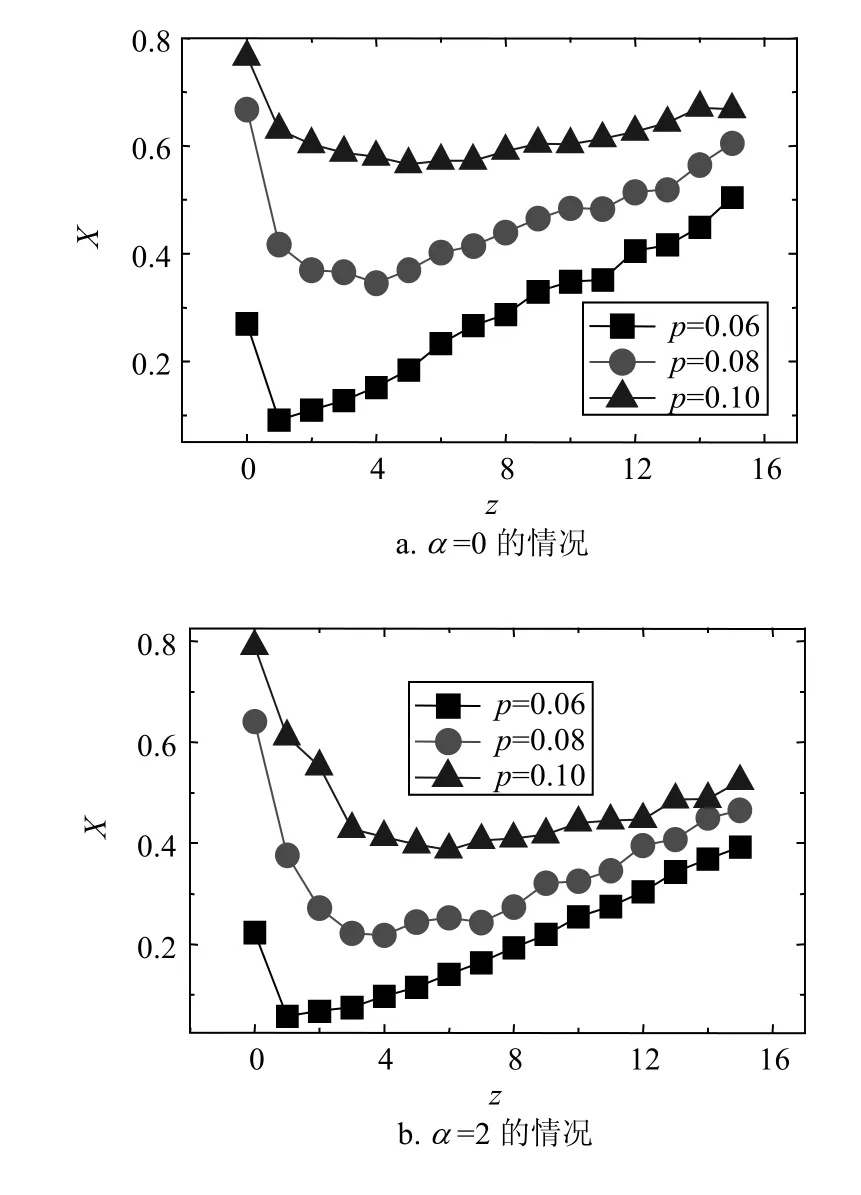
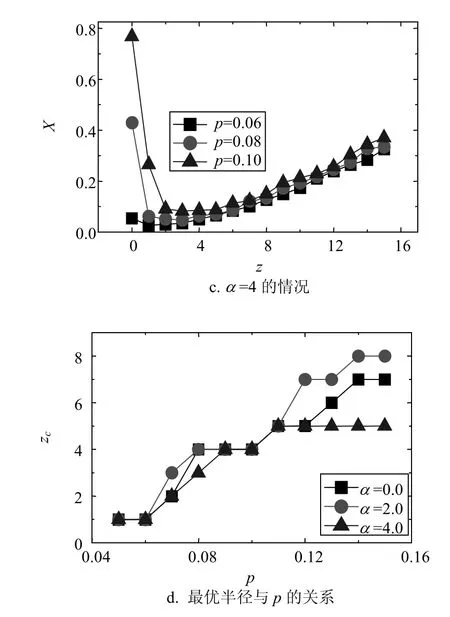
图5 在不同参数α以及传播率p的情况下，总的代价X（X=R（∞）+V（∞）与局部控制半径z的关系

图6 在p=0.1的情形下，总的代价X与参数α及局部控制半径z的关系

图7进一步比较了m=1、m=2与m=3的情况，参数为q=0.5，p=0.08，r=0.1，v=0.1。通过比较可发现，随着m的增加，即长程边数量的增加，疾病更容易扩散（相同的传播率p），因此总的代价函数X也相应增加，即需要更多的成本区控制疾病的传播，这是因为长程边的增加导致疾病更容易传播。随着m的增加，最优现象也变得不太明显，尤其对完全随机（α = 0 ）及m=3、p=0.1的情况（如图7a中三角形曲线所示），此时最优现象已经基本消失。

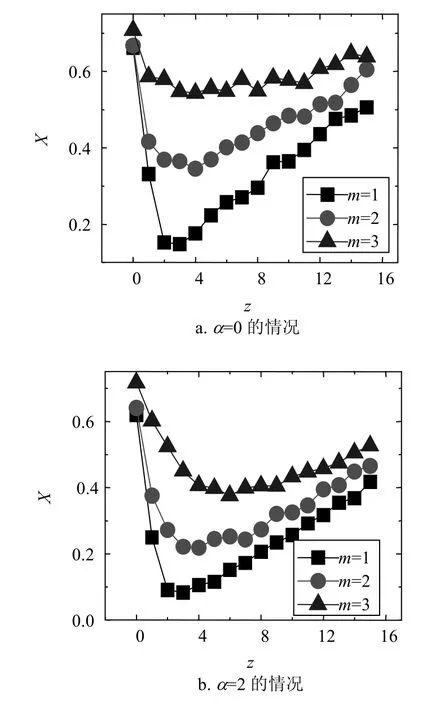
图7 比较长程边数对代价指标X的影响

4 结 束 语

对复杂网络上疾病传播问题的研究方兴未艾［18-20］，而如何有效地控制网络上疾病传播是其中的一个重要课题。已有的研究虽然提出了很多控制策略，但是这些控制策略要么缺乏对控制成本代价的考虑，要么需要充分了解网络的结构信息。基于以上原因，本文在二维的Kleinberg网络上研究一种局部控制策略，通过定义系统总的代价为治愈比例和最终感染比例之和，刻画了控制半径z和总代价X之间的函数关系。

1） 在二维的Kleinberg网络上，当传播率和长程边数量在一定范围内，存在一个最优的控制半径zc使总的代价X最小。当控制半径z过小时，疾病会大范围爆发；当控制半径过大时，虽然疾病被控制，但治愈的成本也会大幅度增加。因而存在最优的控制半径使总的代价最低。2） 最优现象随着参数α的增加变得更为明显，且总的代价也会相应降低。3）最优半径随着传播率的增加而增加，如果进一步增加传播率会导致最优控制半径消失。4） 增加网络中的长程边连接会导致传播范围上升，且最优现象逐渐削弱。

考虑到网络结构、传播动力学、控制成本以及个体自身行为等多种因素的影响，如何最有效地控制疾病传播是值得深入探讨的问题［21-22］，本文将做进一步的探讨。

本文的研究工作得到安徽大学博士基金（01001951）和青年骨干教师培养基金（01005102）的资助，在此表示感谢。

［1］ 李翔. 复杂动态网络传播动力学［J］. 力学进展， 2008，38（6）： 723-732. LI Xiang. Spreading dynamics on complex dynamical network［J］. Advance in Mechanics， 2008， 38（6）： 723-732.

［2］ NEWMAN M E J. Networks： an introduction［M］. New York， USA： Oxford University Press， 2010.

［3］ FU Xin-chu， SMALL M， CHEN Guan-rong. Propagation dynamics on complex networks： models， methods and stability analysis［M］. New York， USA： Wiley Press， 2014.

［4］ ZHOU Tao， FU Zhong-qian， WANG Bing-hong. Epidemic dynamics on complex networks［J］. Progress in Natural Science， 2006， 16（5）： 452-457.

［5］ 汪小帆， 李翔， 陈关荣. 网络科学导论［M］. 北京： 高等教育出版社， 2012. WANG Xiao-fan， LI Xiang， CHEN Guan-rong. Network science： an introduction［M］. Beijing： Higher Education Press， 2012.

［6］ 荣智海， 唐明， 汪小帆， 等. 复杂网络2012年盘点［J］. 电子科技大学学报， 2012， 41（6）： 801-806. RONG Zhi-hai， TANG Ming， WANG Xiao-fan， et al. Review of complex network researches in 2012［J］. Journal of University of Electronic Science and Technology of China， 2012， 41（6）： 801-806.

［7］ WANG Lin， LI Xiang. Spatial epidemiology of networked metapopulation： an overview［J］. Chin Sci Bull， 2014， 59（28）：3511-3522.

［8］ PASTOR-SATORRAS R， VESPIGNANI A. Immunization of complex networks［J］. Phys Rev E， 2002， 65： 036104.

［9］ COHEN R， HAVLIN S， BEN-AVRAHAM D. Efficient immunization strategies for computer networks and populations［J］. Phys Rev Lett， 2003， 91： 247901.

［10］ GONG Kai， TANG Ming， HUI P M， et al. An efficient immunization strategy for community networks［J］. PLOS ONE， 2013， 8（12）： e89066.

［11］ ZHANG Hai-feng， LI Ke-zan， FU Xin-chu， et al. An efficient control strategy of epidemic spreading on scale-free networks［J］. Chin Phys Lett， 2009， 26（6）：068901.

［12］ MÜLLER J， SCHÖNFISHCH B， KIRKILIONIS M. Ring vaccination［J］. J Math Biol， 2000， 41（2）： 143-171.

［13］ DYBIEC B， KLECZKOWSK A， GILLIGAN C A. Controlling disease spread on networks with incomplete knowledge［J］. Phys Rev E， 2004， 70： 066145.

［14］ NEWMAN M E J， WATTS D J. Renormalization group analysis of the small-world network model［J］. Phy Lett A，1999， 263（4）： 341-346.

［15］ KLEINBERG J. Navigation in a small world［J］. Nature，2000， 406（6798）： 845.

［16］ KLEINBERG J. The small-world phenomenon： an algorithmic perspective［C］//Proc of 32nd Annual ACM Symposium on Theory of Computing. New York， USA：ACM Press， 2000.

［17］ WATTA D J， STROGATZ S H. Collective dynamics of‘small-world' networks［J］. Nature， 1998（393）： 440-442.

［18］ SUN Ye， LIU Chuang， ZHANG Chu-xu， et al. Epidemic spreading on weighted complex networks［J］. Phys Lett A，2014， 378（7）： 635-640.

［19］ ZHANG Zi-ke， ZHANG Chu-xu， HAN Xiao-pu， et al. Emergence of blind areas in information spreading［J］. PLoS ONE， 2014， 9（4）： e95785.

［20］ 王伟， 杨慧， 龚凯， 等. 复杂网络上的局域免疫研究［J］.电子科技大学学报， 2013， 42（6）： 817-830. WANG Wei， YANG Hui， GONG Kai， et al. Local immunization algorithm on complex networks［J］. Journal of University of Electronic Science and Technology of China， 2013， 42（6）： 817-830.

［21］ BULDYREV S V， PARSHANI R， PAUL G， et al. Catastrophic cascade of failures in interdependent networks［J］. Nature， 2010， 464： 1025-1028.

［22］ FUNK S， SALATHÉ M， JANSEN V A A. Modeling the influence of human behavior on the spread of infectious diseases： a review［J］. R Soc Interface， 2010， 7（50）：1257-1274.

编 辑 黄 莘

OEpptiidmeaml iLc oinca Tl wCoo-nDtr imole Sntsriaotneagly K foleri nthbee rSgp Nreeatdwionrgk osf

BAO Zhong-kui and ZHANG Hai-feng
（School of Mathematical Science， Anhui University Hefei 230601）

In this paper we study the spreading of epidemic and its optimal control strategy in two-dimensional Kleinberg networks. We propose a local control strategy based on the Manhattan distance to inhibit the spreading of epidemic in Kleinberg networks， and then study the effect of this strategy on the cost function of total system （defined as the sum of the density of infection and the density of cured individuals）. We find that， when the number of long-distance edges and the transmission rate are in a certain range， there will be an optimal control radius that makes the cost function of total system be minimum. When the control radius is smaller than the optimal radius， the epidemic cannot be effectively controlled， leading to the outbreak of epidemic. However， when the control radius is larger than the optimal radius， the cost of controlling is very high though the epidemic can be controlled. Meanwhile， we also show that the optimal control radius is influenced by the transmission rate and the parameter depicting the Kleinberg network.

cost function； epidemic spreading； Kleinberg networks； local control strategy

TN92； O41

A

10.3969/j.issn.1001-0548.2016.02.028

2014 - 09 - 22；

2015 - 09 - 13

国家自然科学基金（61473001）

鲍中奎（1982 - ），男，博士，主要从事信息处理、信息传播动力学等方面的研究.