改进的Keccak算法4轮区分器

刘景美，薛 宁，赵林森

（1. 西安电子科技大学综合业务网国家重点实验室 西安 710071；2. 西安邮电大学电子工程学院 西安 710061）

改进的Keccak算法4轮区分器

刘景美1，薛 宁1，赵林森2

（1. 西安电子科技大学综合业务网国家重点实验室 西安 710071；2. 西安邮电大学电子工程学院 西安 710061）

Keccak算法是新一代Hash函数标准SHA-3的获胜算法。 如何构造一个好的区分器是当前Hash函数中的研究热点。该文在分析Keccak算法及算法中各个置换性质的基础上，通过线性分析方法和差分分析方法，研究了整体Keccak算法的差分传播特性。利用Keccak旋转变换和z周期性质，成功构造出4轮Keccak置换的区分器。通过分析Keccak算法的旋转对的传播特性，对Morawiecki区分器的构造方法进行了修正改进。实验结果表明该区分随机置换和Keccak变换的区分概率更大，区分效果比Morawiecki构造的区分器区分效果更好。

差分分析； Hash函数； Keccak算法； 随机置换

随着被广泛使用的MD5与SHA-1等Hash算法破解技术的发现，美国国家标准与技术研究院（NIST）发起了新一代密码杂凑算法-（SHA-3）的公开竞赛［1］。SHA-3候选算法在设计消息填充、压缩函数的非线性变换部件时，充分借鉴了MD算法的不足之处，同时采用了新的迭代结构，如sponge、wide pipe和HAIFA等。这些改进措施可以有效地防止相关的多碰撞攻击、原象攻击和第二原象攻击，不仅安全性高，且具有较好的运行效率和适用性。2012年10月NIST确认Keccak算法为SHA-3标准［2］，同时Keccak算法也成为密码分析者攻击的首选对象。文献［3］结合差分分析和代数分析，提出了目标差分攻击，并对Keccak进行了4轮碰撞攻击，扩大了攻击的轮数，在个人PC上几分钟内就可以发现碰撞。目前还存在一些其他相关的分析，如旋转特性分析、区分器构造和缩减轮数攻击等［4-13］。本文在分析Keccak算法中Keccak置换的性质和差分传播特性的基础上，改进了文献［4］中区分器的构造方法，得到了一种区分效果更好的4轮区分器，可以更好地区分Keccak置换和随机置换。

1 Keccak算法介绍

SHA-3算法的评选活动中，NIST对候选算法要求至少包含4种输出长度，n∈（224，256，384，512），把不同参数的Keccak算法根据Hash输出长度的大小分别记作Keccak-224、Keccak-256、Keccak-384、Keccak-512。获选的Keccak算法采用了标准的sponge结构［14］，可将任意长度的输入比特映射成固定长度的输出比特。

图1 海绵结构

Keccak算法采用的海绵结构如图1所示，其中M为任意长度的消息，Z为Hash后的输出， f为Keccak-f［b］的置换函数，r为比特率，c为容量，且brc=+，参数c为Hash输出长度的2倍，即c=2n。从图中可以明显的看出，海绵结构有2个阶段：absorbing（吸收）阶段和squeezing（压缩）阶段。在absorbing阶段，消息M首先被填充，然后被分组，每组有r个比特，同时b个初始状态全部初始化为0。填充规则为在消息M后串联一个数字串100…01，其中0的个数是使得消息M填充后长度为r的最小正整数倍。根据此规则可以发现最小填充的长度为2，最大为r+1。

Keccak算法的内部状态可看作是一个5×5×w的3维比特数组，用 a［5］［5］［w］表示，其结构如图2所示分别有以下7种状态：state、slice、plane、sheet、row、column、lane。获选的Keccak-f［1 600］的状态用a［5］［5］［64］表示。

图2 状态的划分

在海绵结构的吸收阶段，每个消息分组与状态内部的r bit进行异或，然后与后面固定的c比特一起封装成1 600 bit的数据进行轮函数f处理，然后再进入挤压过程。在挤压阶段，可以循环产生n比特固定输出长度的Hash值，其中迭代次数 nr由状态比特数b决定，即nr=12+2l，其中2l=b/25。获选的Keccak-f［1 600］的b=1 600 bit，因此将循环执行24次，每个循环R只有最后一步轮常数不同，但是该轮常数在碰撞攻击时经常被忽略不计。Keccak算法结构如图3所示。

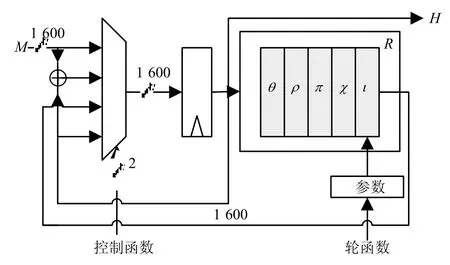
图3 Keccak-f算法结构

从图中可以看出，Keccak-f［1 600］每轮迭代的轮函数R都由5个映射构成，即R=f（l，χ，π，ρ，θ）。下面分别介绍这5个变换。

θ变换：θ是一个线性映射，共涉及11 bit的运算，即：

θ变换的逆运算为θ-1，具有快速的扩散能力，即输入改变1 bit，一半的输出比特值将会被翻转。

ρ旋转：主要是对Keccak的lane进行操作，也就是对lane里面的状态进行移位，即：

π变换：a［x］［y］［z］←a［x′］［y′］［z］，其中：

χ变换：χ变换是Keccak变换中唯一的非线性变换，320个row各自独立进行变换，变换形式为：

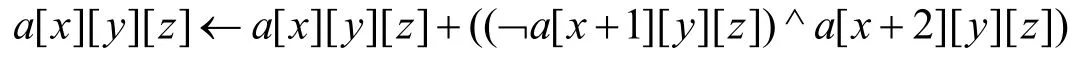
χ变换可以看作是一个关于row的5输入5输出的S盒，该S盒是一个可逆映射，且每个输出比特多项式的代数度数仅为2，χ-1的代数度数为3。

ι变换：可以看作是常数异或的过程，即：

一般在对Keccak算法进行碰撞攻击时，该轮都会被删除，不做特别分析。

2 Keccak旋转对的传播特性与4轮区分器

定义 1 假设Keccak-f［1 600］两个状态为A和A′，如果对每个lane都满足A［x］［y］［x］=A′［x］［y］［（z+n）mod 64］，则A和A′为旋转对。

从定义1中可以看出，最多有64个旋转对，旋转对有可能会导致原象攻击。同时可以看出z的周期为n，记为Rot（A［x］［y］，n）

定义 2 集合Sn为21600个状态对经过若干步Keccak-f［1 600］变换或逆变换所得的所有旋转对状态结果的集合。

定义 3 集合 Sn中任意选定的一对状态（A，A′），则A［x］［y］［z］≠A′［x］［y］［z+n］的概率为：

式（5）可表示为pa=Pr（a0≠a1），其中

给定一个n比特的置换p：｛0，1｝n→｛0，1｝n，任意n比特输入序列产生的所有可能输出结果的集合为Pn，则集合 Pn的基数为

定义 4 设Dn是给定的某种概率分布，若Dn为均匀分布，即p∈Dn的概率Pr（p∈Dn）=1/n！,则p为随机置换。

为了更直观地看出Keccak算法后续过程的概率变化过程，分析Keccak算法中两个最基本的比特运算：AND（与）运算和XOR（异或）运算。设a和b为两个输入比特对，out是a和b经过某种比特间运算的输出比特对， Pout表示输出的两个比特不相同的概率。

对于AND（与）运算，有：

对于XOR（异或）运算，有：

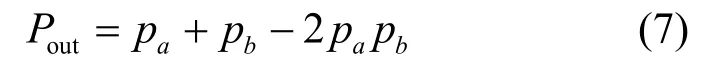
对于NOT（非）运算，并不影响输出概率，它仅仅是翻转相关的输入比特A［x］［y］［x］和A′［x］［ y］［z + n］的值，不改变输入之间的相对关系。同样旋转运算Rot（w，n） 变换只是交换了比特的相对位置，并不改变比特的值，因此根本不影响输出概率。

Keccak-f［1 600］的χ、θ、π 变换都是比特间的运算，如θ变换，只存在异或运算，由于异或运算的线性性，由式（7）可以计算其输出比特不同的概率值。同理，χ变换的输出比特不同的概率都可以用式（6）和式（7）计算。Keccak算法的最后一步是l变换，也就是lane（0，0）异或上一个轮常数，若轮常数为0，相当于没有做任何操作。若轮常数不为0且旋转周期 n＞0，则l变换的异或操作将会改变输出比特对 Pout的概率，且输出概率与Rot（w，n）和“1”的位置有关，设偏移量满足关系：

假设考虑8 bit的旋转对lane，若此时旋转周期n=3，按照定义1，则有∀z：A（0，0，z）=A′（0，0，z 3），因此当A（0，0）=00000010时，有A′（0，0）=00010000，同时根据式（5）有如果A（0，0）和A′（0，0）同时异或一个8 bit的常数C=00100000，则A（0，0）= 00100010，A′（0，0），再经过旋转变换后，对于轮常数为64 bit的Keccak-f［1 600］，该结论依然成立，证明过程也类似。

根据以上这些性质，可以构造一个4轮旋转区分器，用以区分随机置换和Keccak变换。实验结果表明经过4轮迭代之后，对于旋转数n，存在一些坐标（x，y，z）使得p（x，y，x）n不再服从p=0.5的二项分布B(N,p)，从而可以成功地区分出随机置换和Keccak变换。本次实验选取n=54，起始状态通过迭代运算，计算更新每一轮输出状态的p（x，y，x）n，得到4轮区分器的概率变化过程如图4所示。

图4中每一个方格代表每一个比特的p（x，y，x）n概率值，不同灰度颜色与图形标记p（x，y，x）n的大小范围，为了便于绘图和观察，每个lane都选用状态的二维视图，用（x， y）表示，其中一个单一的小方块代表了p的值或范围。Keccak算法共有25个lane，每个lane有64 bit，因此可以看到图中状态可以表示成坐标（25，64），图中每一行都代表一个lane，每一列代表一个slice。例如表示第6排最左边的小方格，而表示最后第25排最右边的小方格。

图4 4轮区分器的概率变化过程

该区分器模拟建立过程中，仿真环境是Pentium（R） Dual-Core CPU E5300 2.6 G，仿真软件采用python，迭代生成得到每一个点数据，再根据它的值加上色彩和不同的图形实现。

在区分器建立的起始时刻，所有旋转对的对应位都相等，根据式（6）和式（7），因此有通过迭代运算，计算更新每一轮的输出状态值。经过首轮ι变换的常数异或后的一部分概率值将会发生改变，并且这些变化在后续的迭代过程中会一直传播并影响其他比特。对于大多数的旋转周期n，在4轮迭代后的部分取值会偏离0.5，但大部分都接近0.5。经过计算仿真，4轮Keccak后也就是最终选取的旋转周期n=54。

为了验证区分器，随机选择20 000个旋转对经过4轮Keccak-f［1 600］变换，发现有11 750个旋转对的比特位有不相同的值。对于一个服从参数为B（N = 20 000， p）的二项分布随机序列，可以得到其样本均值m=10 000，，方差2=712所以经过4轮Keccak-f［1 600］变换得到的均值应该在10 000 ±3×71的范围内，但是显然11 750不在这个置信区间内，从而得出结论：实验结果不符合二项分布B（N，0.5），即可以将Keccak-f［1600］变换从一个随机置换中区分出来，从而成功地构造出4轮Keccak变换的区分器。仿真数据表明，本文选取构造区分器，区分概率比文献［4］选取的0.5 625要大，具有更好的区分效果。

3 结 论

Keccak算法是SHA-3标准的最终获胜算法，到目前为止表现出了良好的抗碰撞攻击性能。它仅存在低轮数的原象攻击和近似碰撞攻击，并未对完整轮数实现实际可行的攻击。本文详细描述了Keccak算法的变换过程和内部轮函数，并且根据Keccak算法置换的旋转变换特性，成功地构造了4轮Keccak算法的旋转区分器，用以区分随机置换和Keccak置换，经过仿真分析得到了比文献［4］更好的区分结果。Keccak完整算法为24轮，且仅存的低轮数碰撞攻击仍具有较高的数据复杂度，因此如何提高攻击的轮数，降低攻击的复杂度，仍然是未来研究的主要热点问题。

［1］ National Institute of Standards and Technology. SHA-3 competition（2007-2012）［S/OL］. ［2014-01-01］. http：//csrc. nist.gov/groups/ST/ hash/sha-3/index.html.

［2］ CHANG Shu-jen， RAY P， WILLIAM E B， et al. Third round report of the SHA-3 cryptographic Hash algorithm competition［M］. Washington， America： U.S. Department of Commerce， 2012.

［3］ DINUR I， DUNKELMAN O， SHAMIR A. New attacks on keccak-224 and keccak-256［C］//19th International Workshop， Fast Software Encryption 2012. Washington：Springer-Verlag， 2012， 7549： 442-461.

［4］ PAWEŁ M， JOSEF P， MARIAN S. Rotational cryptanalysis of round-reduced Keccak［C］//20th International Workshop，Fast Software Encryption 2013. Singapore： Springer-Verlag，2014， 8424： 241-262.

［5］ JEAN J， NAYA P M， PEYRIN T. Improved rebound attack on the finalist grøstl［C］//19th International Workshop， Fast Software Encryption 2012. Washington： Springer-Verlag：2012， 7549： 110-126.

［6］ 李倩男， 李云强， 蒋淑静， 等. Keccak类非线性变换的差分性质研究［J］. 通信学报， 2012， 33（9）： 140-146. LI Qian-nan， LI Yun-qiang， JIANG Shu-jing， et al. Research on differential properties of Keccak-like nonlinear transform［J］. Journal on Communications， 2012， 33（9）：140-146.

［7］ PAWEL S， GERGOR L， CHRISTOF P. Keccak und der SHA-2［J］. Datenschutz Und Datensicherheit， 2013， 37（11）：712-719.

［8］ MARÍA N P， ANDREA R， WILLI M. Practical analysis of reduced-round Keccak［C］//12th International Conference on Cryptology. Chennai， India： Springer-Verlag， 2011， 7107：236-254.

［9］ MOSTAFA T， PATRICK S. Differential power analysis of MAC-Keccak at any key-length［C］//8th International Workshop on Security， IWSEC 2013. Okinawa， Japan：Springer-Verlag， 2013， 8231： 68-82.

［10］ ELENA A， BART M， BART P. Open problems in Hash function security［J］. Designs， Codes and Cryptography，2015， 77（2）： 611-631.

［11］ SUGIER J. Low cost FPGA devices in high speed implementations of Keccak-f Hash algorithm［C］// Proceedings of the 9th International Conference on Dependability and Complex Systems DepCoSRELCOMEX. Runów， Poland： Springer-Verlag， 2014， 286：433-441.

［12］ KUILA S， SAHA D， PAL M， et al. Practical distinguishers against 6-round Keccak-f exploiting self-symmetry［C］//7th International Conference on Cryptology. Marrakesh， Africa：Springer-Verlag， 2014， 8469： 88-108.

［13］ SOURAV D， WILLI M. Differential biases in reducedround Keccak［C］//7th International Conference on Cryptology. Marrakesh， Africa： Springer-Verlag， 2014，8469： 241-262.

［14］ Federal Information Processing Standards Publication. SHA-3 standard： Permutation-based Hash and extendableoutput functions［S/OL］. ［2014-01-10］. http：//nvlpubs.nist. gov/nistpubs/FIPS/NIST.FIPS.202.pdf.

编 辑 叶 芳

Improved 4-Round Distinguisher for the Keccak Algorithm

LIU Jing-mei1， XUE Ning1， and ZHAO Lin-sen2
（1. National Key Laboratory of Integrated Service Networks， Xidian University Xi'an 710071；2. College of Electronic Engineering， Xi'an University of Post & Telecommunications Xi'an 710061）

The Keccak algorithm is selected as the new Hash function standard of SHA-3 fianally. How to construct a good distinguisher is a hot topic in cryptanalysis of the Hash function at present. In this paper， on the base of the permutation property， we research the differential propagation characteristics of the Keccak algorithm by the linear and differential cryptanalysis methods. By using the Keccak rotation transform characteristics and z cycle properties， we construct the distinguisher of the 4-round Keccak permutation successfully. Then we improve the 4-round Morawiecki' distinguisher of the Keccak algorithm by using the propagation characteristics of the rotational pair. The research results show that our improved rotational distinguisher can distinguish the random permutation from the Keccak permutation with a higher probability， and the distinguish effect is better than Morawiecki's distinguisher.

differential cryptanalysis； Hash function； Keccak algorithm； random permutation

TP309

A

10.3969/j.issn.1001-0548.2016.02.024

2014 - 05 - 22；

2015 - 11 - 20

国家自然科学基金（60903199）；高等学校创新引智基地基金（B08038）；国家留学基金委项目（201506965088）

刘景美（1979 - ），女，博士，副教授，主要从事密码分析与网络安全方面的研究.