噪声相关粒子滤波算法

李 伟，曹 洁，李 军，王进花

（兰州理工大学电气工程与信息工程学院 兰州 730050）

噪声相关粒子滤波算法

李 伟，曹 洁，李 军，王进花

（兰州理工大学电气工程与信息工程学院 兰州 730050）

对标准粒子滤波在处理非线性系统状态估计中噪声独立假设的局限，该文研究分析了一种噪声相关粒子滤波算法。在常用的系统状态模型基础上，分析了噪声相关时建议分布函数的具体分布形式，并以高斯相关噪声为背景，在重要性权重条件最小方差意义下推导了最优建议分布函数的数值表达式。所设计的滤波器有效弥补了传统粒子滤波算法在噪声相关情况下的缺陷，拓展了PF算法的应用范围。仿真实验表明了该方法的有效性。

噪声相关； 非线性系统； 粒子滤波； 建议分布函数

粒子滤波器是一种新兴的非线性滤波方法，其核心思想［1-2］是采用一系列赋予相应权重信息的随机采样粒子以加权求和的方法近似系统的后验状态概率密度函数，在最小均方误差的准则下实现系统状态的估计。与目前普遍采用的扩展卡尔曼滤波器（extended kalman filter， EKF）和无迹卡尔曼滤波器（unscented kalman filter， UKF）等采用线性近似技术的非线性滤波方法相比，该算法摆脱了对系统线性、高斯特性的假设，理论上可以适应任意的非线性非高斯系统。近年来，随着计算机处理能力的增强，该算法在目标跟踪［3-8］领域得到了广泛的应用。

传统PF算法为了采样和计算的方便，通常选用系统状态一步转移概率作为建议分布函数进行采样处理。虽然该方法易于实现，但是其滤波精度严重依赖于系统模型，当模型建立误差较大时，由于选取的建议分布函数缺乏最新观测信息的修正作用，多次迭代后容易导致系统模型失配误差增大，最终产生所谓的“粒子权值退化”问题，滤波估计精度大幅降低，甚至出现发散。因此，如何选取优秀的建议分布函数，是该算法的一个核心研究内容。近年来，针对建议分布函数的选取问题，研究人员提出了一系列的改进算法。如文献［2］采用EKF对采样粒子进行滤波处理，通过近似非线性滤波的方法融入当前的观测信息来调整不同粒子的权重信息，实现了建议分布函数的优化处理，提出了一种扩展卡尔曼粒子滤波算法（extended kalman PF， EPF），一定程度上克服了因缺乏最新观测信息导致的模型失配问题。但是由于该算法需要通过复杂的雅克比矩阵计算来近似非线性状态，一定程度上影响了算法的改进效果，特别是在强非线性系统中，其滤波效果较差。文献［3］借鉴EPF算法的改进思想，采用无迹卡尔曼滤波器对采样粒子进行滤波更新，提出了一种无迹卡尔曼粒子滤波算法（unscented kalman PF，UPF），由于UT变换能将非线性系统的性能精确到3阶的精度，而且不需要计算复杂的雅克比矩阵，一定程度上消弱了EKF近似带来的误差，并且提升了算法的滤波精度。文献［4］在文献［3］的基础上将这种确定的UT变换方法引入到噪声空间内进行计算，得到了一种新型的无迹粒子滤波算法，该算法在确保精度的同时，有效降低了算法的时间消耗。

虽然以上这些改进算法一定程度上消弱了因重采样带来的权值退化问题，在具体应用中提升了算法的总体滤波精度，但这些研究均是在假设系统噪声和测量噪声为相互独立的高斯白噪声的情况下展开的。实际应用中，由于对测量信息进行离散化处理以及受内外环境的影响，噪声相互独立的条件很难得到满足，当系统噪声与测量噪声相互关联时，SPF算法将会产生较大的误差甚至发散［9］。因此，讨论噪声相关情况下的PF问题是非常具有理论意义和现实意义的。

本文首先详细分析了系统噪声与测量噪声之间的关系，理论上分析了状态过程噪声与测量噪声以及它们在时间序列上的相关性，并给出噪声相关情况下的系统状态模型和噪声联合概率密度的分解表达式；然后，深入分析了噪声相关时建议分布函数的的性质，并以高斯相关噪声为背景，在重要性权重条件最小方差意义下推导了噪声相关情况下的最优建议分布函数；最后，提出了噪声相关粒子滤波器（correlative noises PF， CN-PF），给出了新算法的具体实现步骤，并基于数值仿真的方法对算法的性能和统计特性进行了分析。

1 问题描述

1.1 问题提出

在分析非线性滤波方法中，通常可以将时间离散的非线性系统表示为［10］：

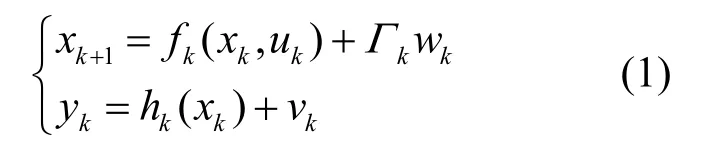
式中，xk、yk为k时刻系统的状态值和观测值； f（·）、h（·）为相应的动态传递函数； uk为模型的控制参量，wk、 vk为相应的过程噪声和量测噪声；Γk为过程噪声的输入控制参量。本文的主要目的是针对式（1）描述的非线性系统，从测量噪声和过程噪声的相关性分析滤波的具体实现方法。借鉴文献［10］，针对式（1）给定的非线性系统，给出两种噪声统计特性的假设。

假设1：如果过程噪声wk与量测噪声 vk是相互关联的高斯白噪声，相关参量采用矩阵形式表示，其相互的统计特性为：

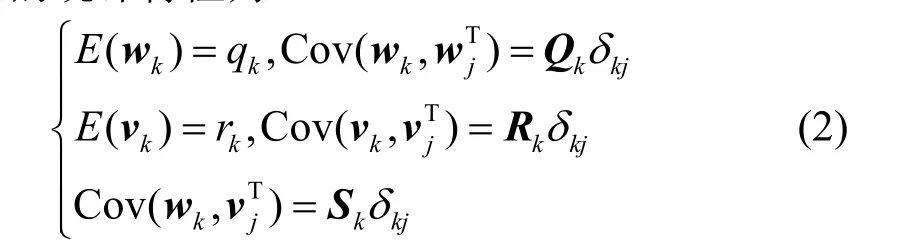
式中，Qk为wk的协方差值矩阵，为对称非负定阵；Rk为 vk的协方差值矩阵，为正定对称矩阵；Sk为wk与 vk之间的互相关系数矩阵； δkj为kronecker函数，满足特性：

假设2：系统的初始状态x0、过程噪声wk、量测噪声 vk之间是互补相关的，并且服从高斯正态分布，其均值和协方差可以表示为：

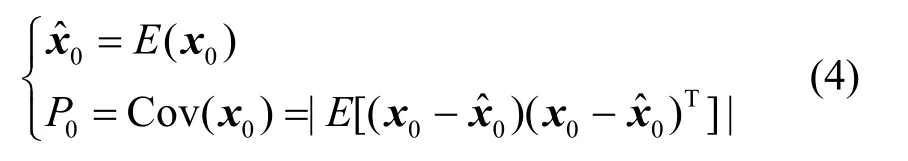
在满足两个假设的前提下，本文的主要目的是在给定最新观测信息Yk+1=｛y1，y2，，yk+1｝的条件下，针对噪声相关情况下的滤波实现问题展开研究，在最小均方误差估计准则下利用最新量测信息给出系统的最终估计值k+1。

1.2 标准粒子滤波算法

标准粒子滤波算法（SPF）采用一簇赋予权值的粒子进行加权求和来近似系统的后验状态，理论上该方法可以处理任何非线性、非高斯系统的状态估计问题［2］，其核心步骤主要包括“预测”和“更新”两个步骤。在给定系统建议密度函数的基础上，通过采样的方法获取一簇赋予权值的粒子集合近似系统的后验分布为进行权值分配的粒子集合，为赋予粒子的权值，满足，系统的状态可以表示为在获取最新观测信息Yk=｛y1，y2，，yk｝的基础上，系统的后验估计为：

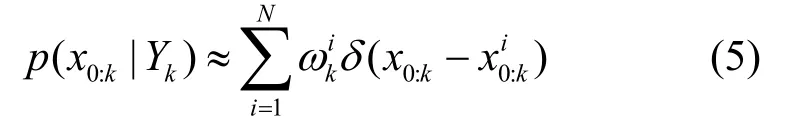
权值计算为：

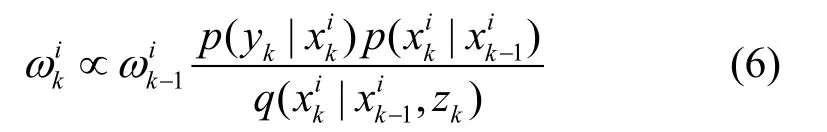
式中， q（xk|·）为进行采样选择的重要性概率密度函数。在SPF中，通常为了计算的方便，将式（7）所表示的一步转移概率密函数选择为先验分布进行采样：

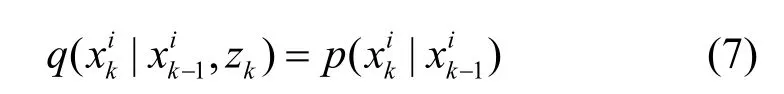
将式（7）代入式（6），可以获取权值的更新表达式为：

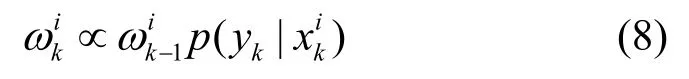
在当前针对PF展开的研究中，多数假设 vk、 ek满足相互独立的高斯特性，且qk=rk=0。

2 噪声相关粒子滤波算法

2.1 噪声相关情况分析

为进行滤波性能的分析，系统模型中将噪声作为加性高斯噪声处理，为了便于分析系统状态估计与噪声之间的关系，可以忽略式（1）中的控制参量，将其进一步简化为：

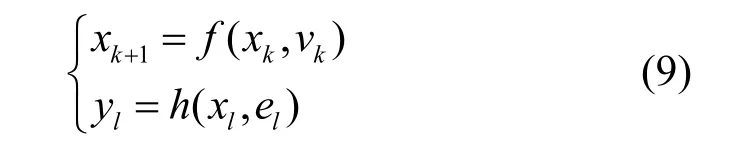
式中， xk、 xl为不同时刻的状态值； yl为当前时刻的观测值； vk、 el为相应的过程噪声与观测噪声。进一步可以将观测信息与状态值之间的联合后验概率密度表示为：

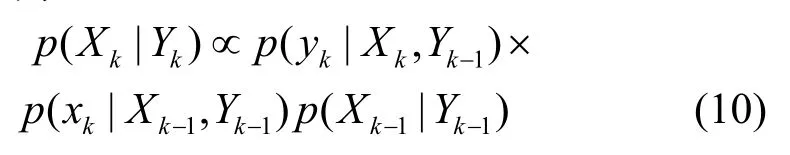
如果满足独立的假设，基于马尔科夫模型，可以将系统模型的相关概率密度函数表示为：

将式（9）表示的动态过程用图1的相互关系表示，可以看出噪声相互关系的传递流程。

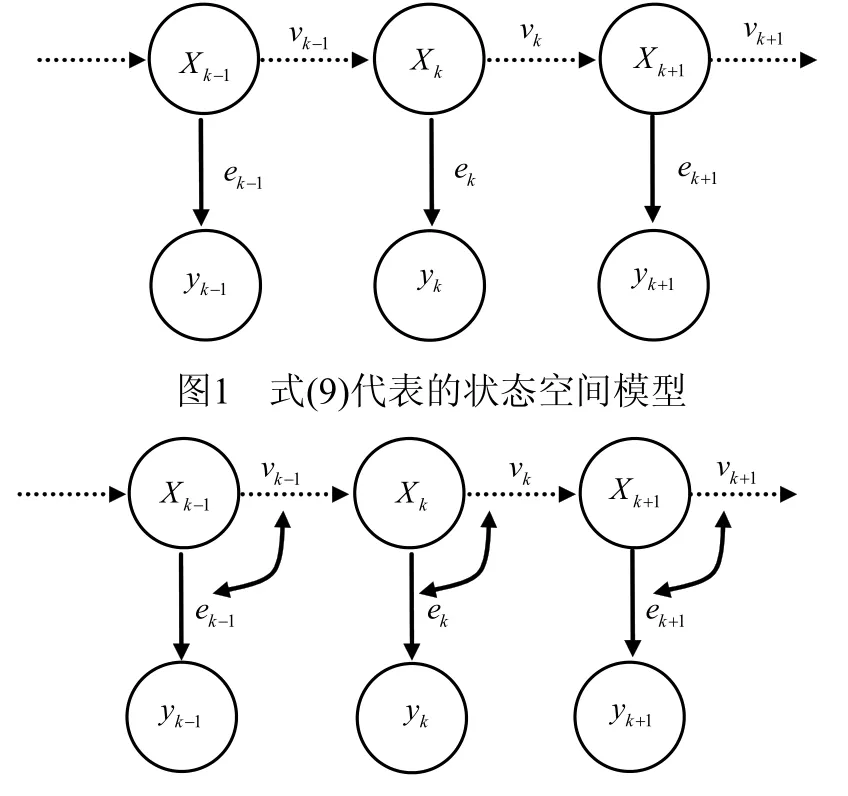
图2 过程噪声和量测噪声相关性示意图

过程噪声和量测噪声相关性示意图如图2所示，可以看出，过程和观测之间的相关性主要表现为噪声时间上的关联性。考虑噪声v1-k和ek-1关联性的主要目的是为了分析噪声联合概率密度函数p（vi，ej）的具体实现形式。

给定噪声向量序列（vk-1，ek-1）T，假设序列之间满足独立性的假设，则：

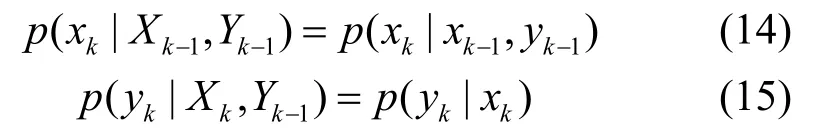
可以进一步将过程与观测的联合概率密度函数表示为：

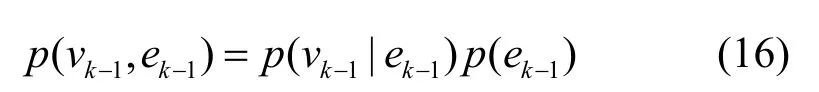
2.2 最优建议分布函数的理论分析

SPF算法的核心思想就是通过对建议分布函数进行采样，通过赋予相应的权重信息，然后通过加权求和的形式逼近系统状态的后验状态分布，可见，建议分布函数的选取决定着算法的整体性能［12］。因此，在考虑噪声相互关联的情况下对系统状态建议分布函数的选择进行理论分析，将（9）式重新表示为：

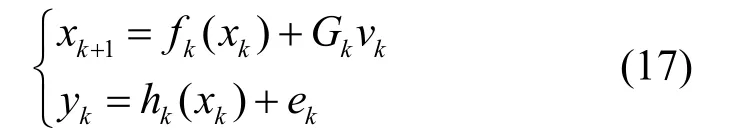
式中，vk和 ek是相关的。根据图2显示的相关性的时间关系，将噪声相关性表示为p（yk，xk+1|xk），因为噪声相关性的存在，在给定当前时刻系统状态 xk的条件下，获取的观测信息yk和xk+1无法满足独立的条件，则：

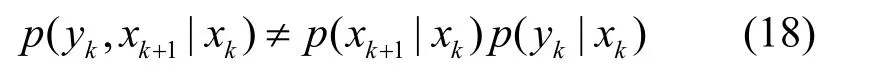
为了采样的方便，SPF中采用的建议分布函数为q（xk|Xk-1，Yk）。文献［12］指出，因为多数非线性系统的状态仿真均满足马尔科夫特性，所以有：

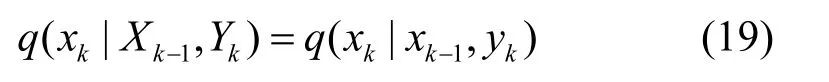
考虑到yk-1和 xk的关系，将式（19）重新表示为：

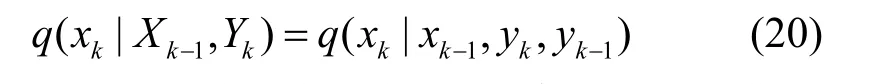
根据贝叶斯滤波思想，结合SPF建议分布函数的形式，考虑噪声相关特性情况下的后验建议分布函数为：

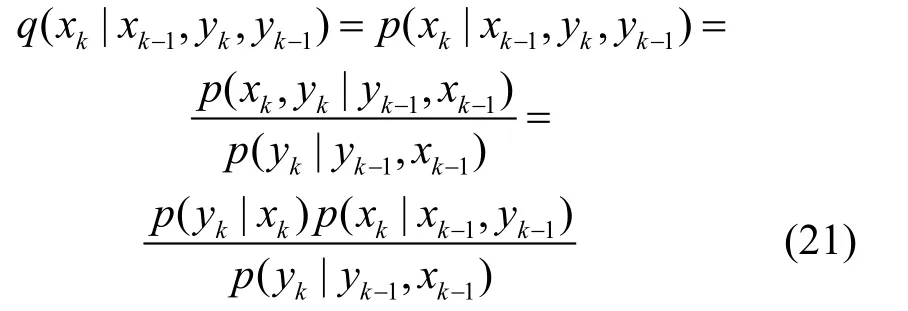
将噪声相关情况下的最优建议分布函数表示为：

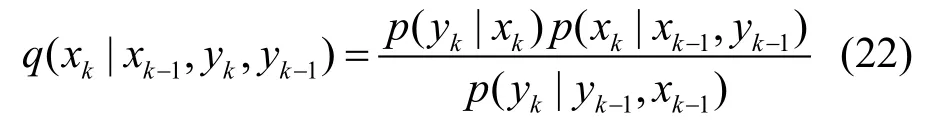
2.3 最优建议分布函数的抽样实现

SPF算法中为了进行抽样解析，假设噪声统计特性满足高斯假设。为了分析本文方法的可行性，同样假设噪声满足高斯特性，即：

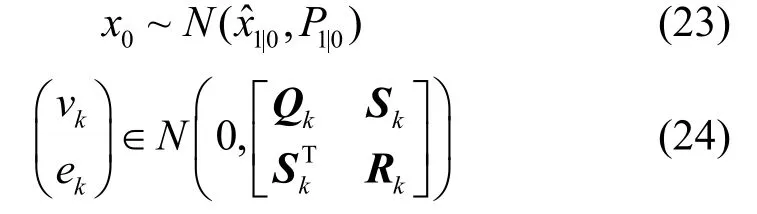
写成分布函数的形式为：

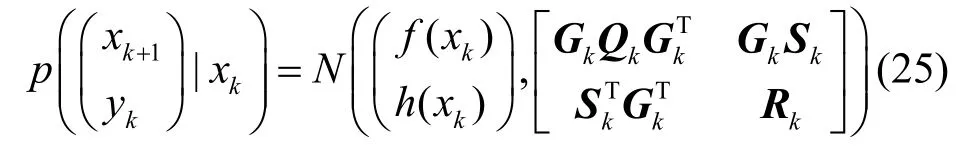
可以看出，噪声是否相关主要取决于 Sk取值，当Sk=0即为SPF,当Sk≠0即为本文讨论的相关噪声情况。假设X、Y的分布满足联合高斯特性，则：

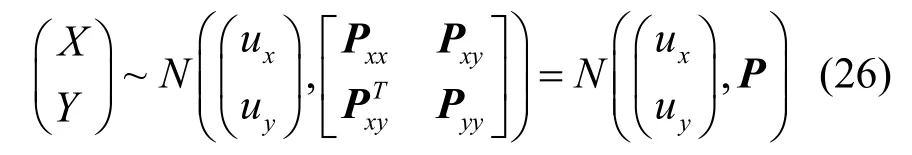
根据式（21）的分解思路，可以在给定观测信息Y=y的条件下，将X的条件分布表示为：

令X=xk|xk-1,Y=yk-1，则有：

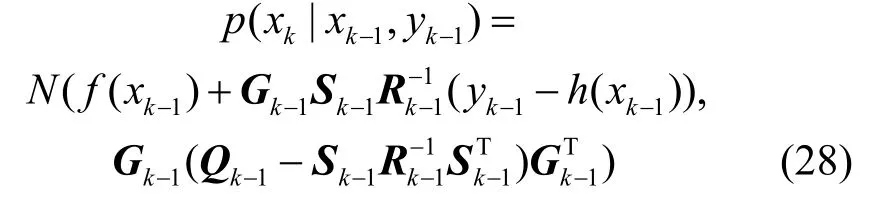
即建议分布函数为：

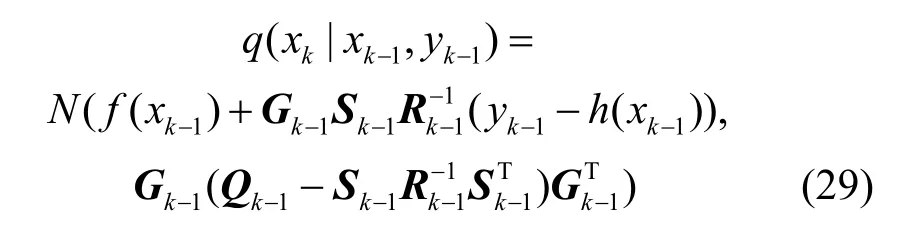
为进行解析采样，则在高斯噪声条件下的最优建议分布函数可以表示为：

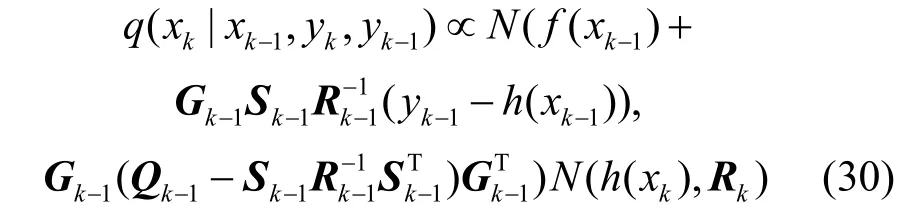
2.4 算法实现步骤

根据前面的理论分析，结合SPF的具体实现步骤，可以将CN-PF的具体实现步骤描述如下：

1） 初始化

2） 权值更新：

k=k+1，从式（29）中按照式（31）进行采样，并按照式（32）更新权值

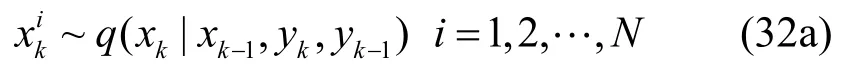
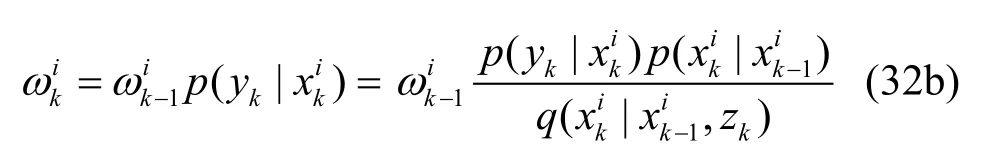
归一化为：

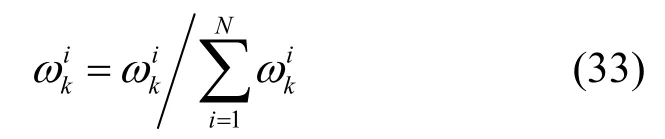
3） 重采样：

根据SPF中克服权值衰退的思想，同样采用重采样的方法缓解退化问题，设定初始阈值Nthreshold如果满足然后将权重粒子集合重新标记为

4） 估计输出：

3 数值仿真分析

为对本文方法的性能进行分析，文献［10］采用式（36）所示的非线性高斯模型进行数值分析：

式中，ωk和 vk均为高斯白噪声。统计特性满足：

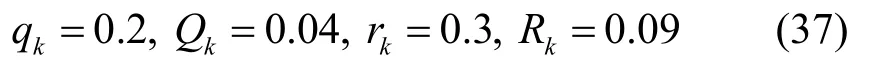
按照文献［10］的描述，将相应的参数值设置为：

状态的初始估计值为：

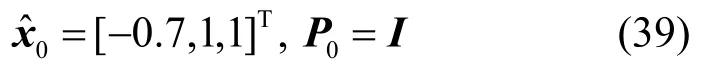
3.1 噪声独立仿真

由式（24）可知噪声不相关特性可以表示为Sk=0，为进行算法性能的分析，首先针对状态 x1进行滤波估计分析，并将估计结果同常用的非线性滤波EKF、SPF方法进行对比分析，具体的估计结果如图3～图5所示。可以看出，在噪声不相关的情况下，3种算法都能够实现系统的有效跟踪，但是EKF的误差明显大于SPF和本文方法。从图4和图5中可以看出，虽然认为SPF为CN-PF在噪声独立情况下的特列，但是该模型仿真的结果显示CN-PF的精度仍然高于SPF，其主要原因是本文方法在分析滤波估计结果时考虑到了时间序列的相关性，这种相关性存在着一阶或二阶记忆效应，但SPF方法忽略了所有的时序特性。在独立假设中，CN-PF只是忽略了一阶时间相关性，仍然保持了二阶以上的解析特点，所以两种方法的精度基本相同。

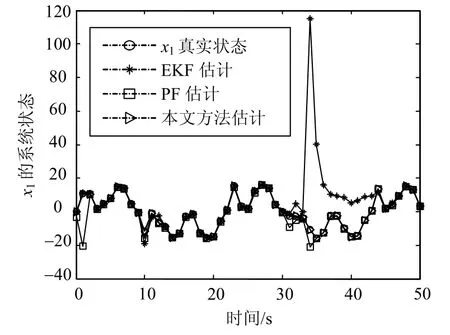
图3 状态 x1的估计曲线

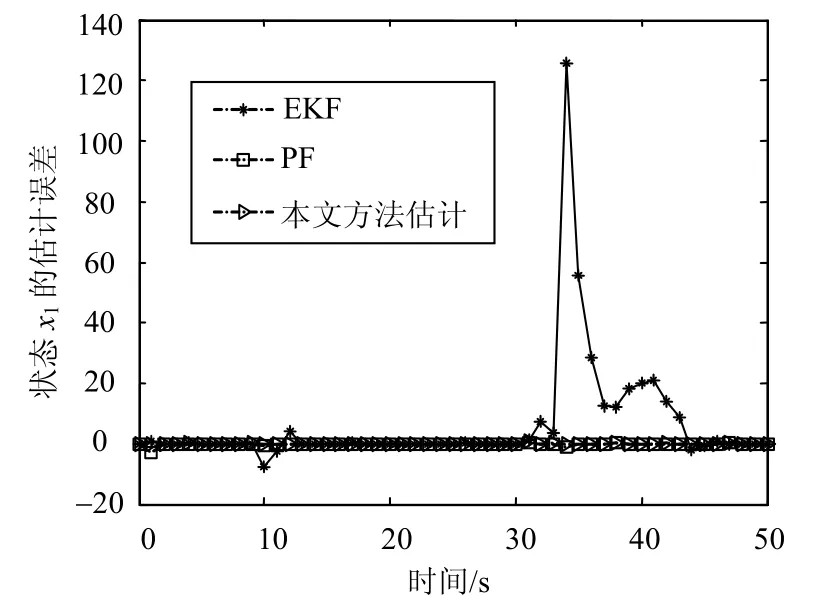
图4 状态 x1的跟踪误差曲线

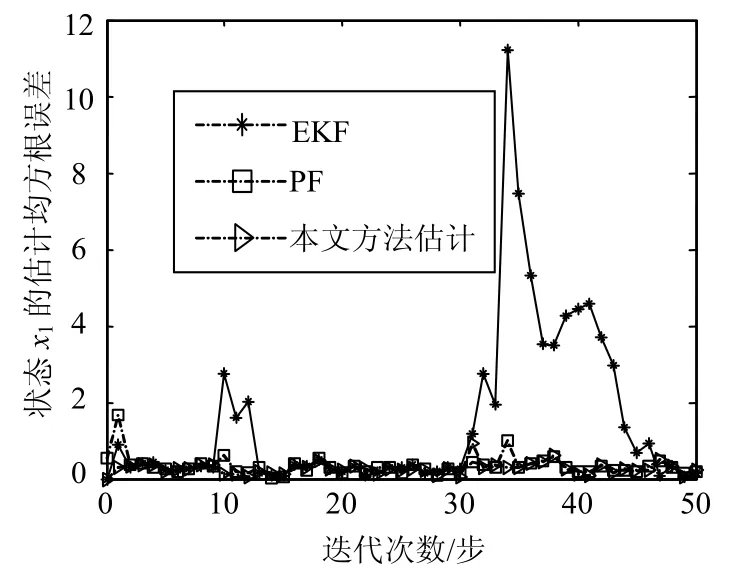
图5 状态 x1跟踪均方误差跟曲线

3.2 噪声相关仿真

噪声相关性可以表示为Sk≠0，为了进行噪声相关性的分析，取Sk∈［0 1］，对状态 x3进行状态估计，具体的估计结果如图6～图8所示。

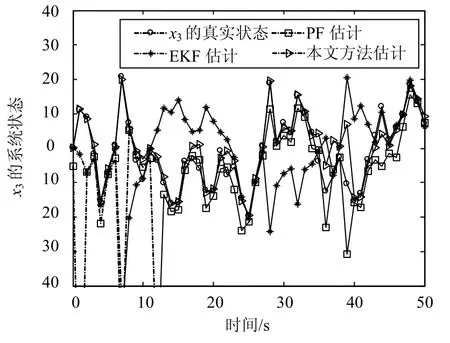
图6 状态 x3的状态估计曲线

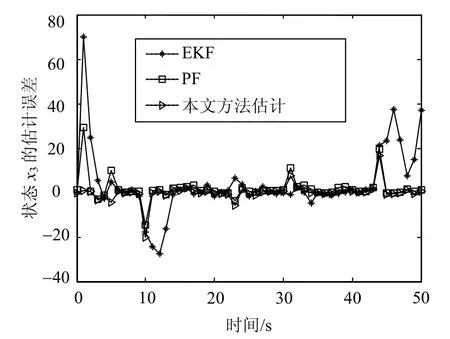
图7 状态 x3的跟踪误差曲线

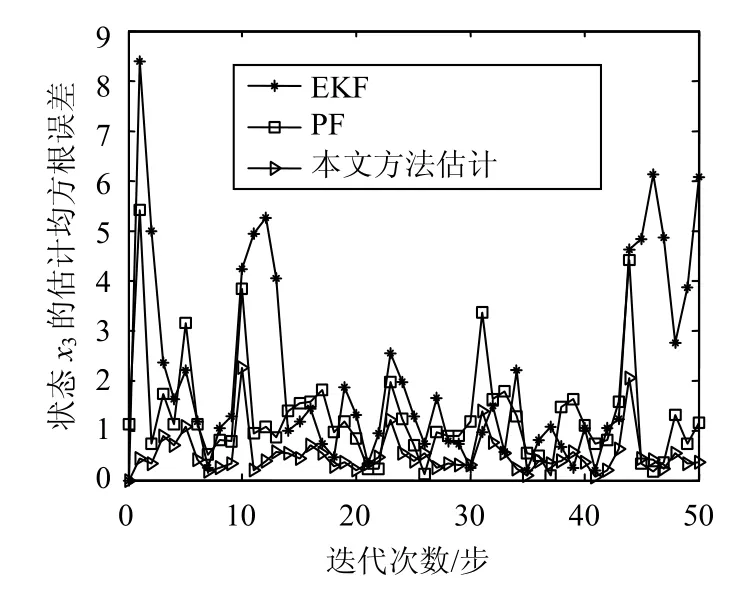
图8 状态 x3的跟踪均方误差根曲线

由图6、图7的估计结果可以看出，噪声相关的时候，容易引起模型失配，EKF、SPF的估计偏差明显增大，但是本文方法保持了较好的估计精度。从图8的统计均方根误差可以看出，随着迭代时间的延长，传统方法均产生了较大的误差累积，本文方法的均方误差较小，保持了较好的滤波精度。

4 结 论

针对非线性、非高斯系统的滤波问题，PF算法提供了一种有效、方便的高效算法。但传统标准PF算法要求系统噪声和量测噪声必须为互不相关的高斯白噪声，该局限性限制了其具体的应用范围。针对传统PF算法在噪声相关情况下滤波精度大幅下降的问题，本文详细分析了系统噪声与量测噪声相关情况下的非线性滤波问题，主要做了以下3个方面的工作：1） 分析了噪声相关的时序特性，并基于现有的模型分析了相关噪声建议分布函数的性质；2）在理论上分析了噪声相关情况下的联合概率密度函数，并进行了解析分解形式的分析；3） 基于SPF思想，在高斯统计特性的条件下，给出了非线性系统模型采样的解析形式及噪声相关粒子滤波器的详细实现步骤。由于本文是对标准PF算法适应范围的扩展，因此很容易结合当前已经存在的很多优化思想提升该算法在不同领域的应用。在下一步的研究中，将研究该算法在系统噪声统计特性未知情况下的最优滤波问题。

［1］ DOUCET A， GODSILL S J， ANDRIEU C. On sequential Monte Carlo sampling methods for Bayesian filtering［J］. Statistics and Computing， 2000， 10（3）： 197-208.

［2］ ARULAMPALAM M S， SIMON M， NEIL G. A tutorial on particle filters for on line non-linear/non-gaussian Bayesian tracking［J］. IEEE Transactions on Signal Processing， 2002，50（2）： 174-188.

［3］ JULIER S J， UHLMANN J K. Unscented filtering and nonlinear estimation［J］. IEEE Trans Signal Processing， 2004，92（3）： 401-422.

［4］ 曲彦文， 张二华， 杨静宇. 改进的无迹粒子滤波算法［J］.控制理论与应用， 2010， 27（9）： 1152-1158. QU Yan-wen， ZHANG Er-hua， YANG Jing-yu. Improved unscented particle filter［J］. Control Theory & Applications，2010， 27（9）： 152-1158.

［5］ WU Chun-lin， HAN Chong-zhao. Quadrature Kalman particle filter［J］. Journal of Xi'an Jiaotong University， 2009，43（2）： 25-28.

［6］ WEI Qi， XIONG Zhang， LI Chao， et al. A robust approach for multiple vehicles tracking using layered particle filter［J］. International Journal of Electronics and Communications，2011（65）： 609-618.

［7］ 杨小军， 邢科义. 无线多跳传感器网络下基于粒子滤波的信道容错的目标跟踪方法［J］. 自动化学报， 2011， 37（4）：440-448. YANG Xiao-jun， XING Ke-yi. Channel fault tolerant target tracking in multi-hop wireless sensor networks based on particle filtering［J］. Acta Automatica Sinica， 2011， 37（4）：440-448.

［8］ KIRCHMAIER U， HAWE S， DIEPOLD K. Dynamical information fusion of heterogeneous sensors for 3D tracking using particle swarm optimization［J］. Information Fusion，2012， 12（4）： 275-283.

［9］ GUSTAFSSON F. Particle filter theory and practice with positioning applications［J］. IEEE Aerosp Electron Syst Mag，2010， 25（7）： 53-82.

［10］ 王晓旭， 赵琳， 夏全喜. 噪声相关条件下Unscented卡尔曼滤波器设计［J］. 控制理论与应用， 2010， 27（10）：1362-1368. WANG Xiao-xu， ZHAO Lin， XIA Quan-xi. Design of unscented Kalman filter with correlative noises［J］. Control Theory and Applications， 2010， 27（10）： 1362-1368.

［11］ YUAN Qin-xia， ZHI Hong-deng， LI Li， et al. A new continuous-discrete particle for continuous-discrete nonlinear systems［J］. Information Sciences， 2013， 242：64-75.

［12］ DESBOUVRIES F， PIECZYNSKI W. Particle filtering with pairwise Markov processes［C］//IEEE Int. Conf. Acoust， Speech， Signal Process （ICASSP）. Hongkong，China： IEEE， 2003， 4： 6-10.

编 辑 叶 芳

Particle Filter Algorithm with Correlative Noises

LI Wei， CAO Jie， LI Jun， and WANG Jin-hua
（College of Electrical and Information Engineering， Lanzhou University of Technology Lanzhou 730050）

The standard particle filter needs to meet the requirement of noise independent. In order to overcome this limitation， this paper proposes a correlative noise particle filter （CN-PF） algorithm. The method analyzes the characteristic of noise time correlation， and derives the joint probability density function of correlative noise based on the given nonlinear system model. The concrete implementation method of noise de-correlation is analyzed based on the Gaussian noise assumption. The optimal proposal distribution function is deduced in the condition of the importance weight variance minimum. The CN-PF algorithm compensates the shortage of the traditional particle filter algorithm effectively， and expands the application range of the PF algorithm. The theoretical analysis and simulation results show the effectiveness of the propose method.

noise correlation； nonlinear system； particle filter； proposal distribution function

TP391

A

10.3969/j.issn.1001-0548.2016.02.021

2012 - 12 - 08；

2016 - 01 - 11

国家自然科学基金（61263031）；甘肃省自然科学基金（1010RJZA046）；甘肃省教育厅研究生导师基金（0914ZTB003）

李伟（1982 - ），男，博士生，主要从事多源信息融合、非线性控制理论与仿真方面的研究.