基于相位滞后补偿的有源电力滤波器性能提高研究

朱朝文，袁海文，郭 鑫，马 钊，周莉梅

（1. 北京航空航天大学自动化科学与电气工程学院 北京 海淀区 100191；2. 中国电力科学研究院 北京 海淀区 100192）

基于相位滞后补偿的有源电力滤波器性能提高研究

朱朝文1，袁海文1，郭 鑫1，马 钊2，周莉梅2

（1. 北京航空航天大学自动化科学与电气工程学院 北京 海淀区 100191；2. 中国电力科学研究院 北京 海淀区 100192）

分析了引起有源电力滤波器（APF）补偿电流相位滞后的原因，建立了相应数学模型，并利用MATLAB仿真研究了相位滞后对有源电力滤波器补偿性能的影响，提出了一种输出补偿电流零相位滞后的超前校正方法，实现了与电源中相应分量的相位同步。最后通过仿真和实际工程应用，证明了该补偿方法的可行性和有效性。

有源电力滤波器； 谐波； 超前校正； 性能； 相位滞后

有源电力滤波器（APF）主要用来动态、实时滤除非线性负载引起的电源系统中的谐波和无功电流，是目前公认的治理和改善电力系统电能质量最有效的手段，其性能显著，效果突出，具有无源滤波器、功率因数校正等传统谐波抑制装置无可比拟的优势［1-3］。然而，其谐波滤除功能的实现是以补偿电流与电源中谐波及无功分量相位同步为基础的，性能及效率补偿程度成为其能否获得广泛应用的一个极其重要的因素。

有源电力滤波器是一个对实时性要求很高的系统，其补偿性能主要取决于系统谐波电流的提取算法。现阶段，关于有源电力滤波器谐波提取算法以及在提高算法的快速性与准确性上有着丰富的研究成果［4-7］。谐波电流提取算法分为经典和现代智能算法，经典算法包括日本学者最早提出的基于瞬时无功理论的谐波提取算法、基于带通（陷波）滤波器的选频算法和基于快速傅里叶变换的频域算法；现代智能算法主要在谐波提取中引入了小波变换、神经元网络以及自适应理论等一些智能手段［8-9］。以上各种算法虽然能够有效进行谐波提取，并且某些算法也具有较高的实时性和快速性，但是由于每种算法本身的特性以及算法实现过程中的时间消耗，加上整个系统中其他单元的时间延迟，最终会导致补偿电流中不可避免地出现相位滞后，从而限制了有源电力滤波器整体的补偿性能。因此，研究有源电力滤波器中克服时序滞后的输出电流相位补偿方法，对进一步提高有源电力滤波器补偿性能，进一步扩大其工程应用范围具有重大意义。

本文首先分析了导致有源电力滤波器补偿电流相位滞后的原因，研究了相位滞后数学模型对补偿性能的影响；提出了相位超前校正补偿方法，实现了输出补偿电流与电源侧电流分量的相位同步；最后通过仿真研究和实际工程应用，证明了该方法切实可行。

1 APF输出补偿电流相位滞后原因分析

有源电力滤波器的补偿输出电流主要经历负载电流采集、补偿电流提取、电流调节控制、主功率逆变4个单元［10-11］，其原理框图如图1所示。其中，iAL、 iBL、iCL为三相负载电流， iAS、 iBS、 iCS为三相电源电流， iAC、 iBC、 iCC为APF输出的三相补偿电流，L为三相功率电感。负载电流采集单元由3个电流互感器实现。电流互感器功能依据电磁感应原理工作，其检测到的电流有效值呈比例（倍数）关系，而电流相位相比一次侧电流有滞后现象。因此，通过负载电流采集单元后，检测到的电流相位比原电流分量有一定程度的滞后。

图1 有源电力滤波器工作原理

补偿电流提取单元主要在嵌入式测控系统中完成。嵌入式处理器先将采集的模拟信号离散化，经过谐波提取算法提取要补偿的谐波和无功分量，最后数模转换成给定基准信号输出。系统无论采用哪种提取算法，都不可避免产生时间延迟，最后输出的电流给定基准信号都会有不同程度的相位滞后。

电流调节控制和主功率逆变单元中，一方面为了避免主功率管上、下桥臂的直通故障，会在功率驱动信号中加入死区时间；另一方面，功率器件并非理想，会有微小的开通及关断时间。随着开关管高频导通与截止，这些时间延迟逐渐累积会使逆变输出的补偿电流有一定程度的相位滞后。

综上所述，补偿输出电流通过以上环节后，有源电力滤波器实际注入到电源侧的电流相位滞后于装置需要补偿的电流，电流相位的偏差会引起幅值的畸变，最终会降低APF整体的补偿效果。

2 补偿输出电流相位滞后研究

2.1 相位滞后模型

设A相电源电压为UAS（t）=Usin（ωt），由APF的工作原理可得A相非线性负载电流为：

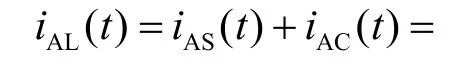
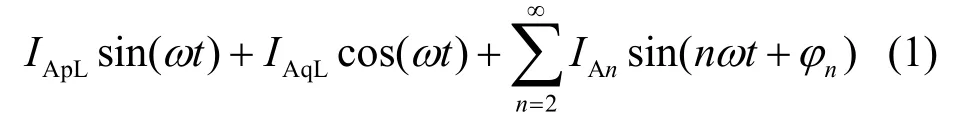
式中，

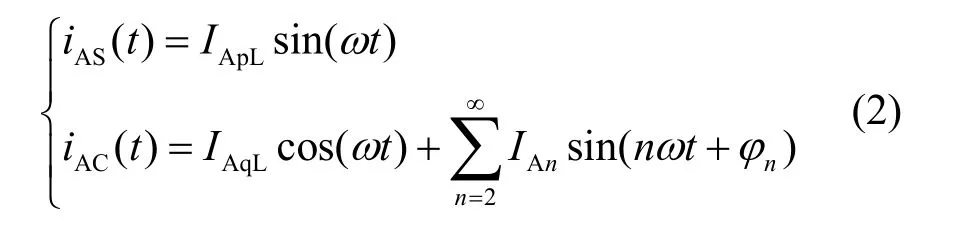
IApLsin（ωt ）为基波有功电流； IAqLcos（ωt）为基波无功电流；）为谐波电流。假定不考虑补偿电流与需要补偿分量幅值之间的影响，即补偿输出的电流幅值与电源中谐波及无功分量幅值相同，仅相位有滞后，此时补偿输出电流为：

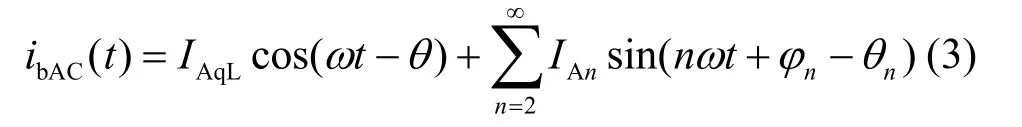
式中， IAqL、 IAn为无功电流、谐波电流幅值；θ、θn分别为无功电流、谐波电流滞后电源电流中相应分量的相位角，即相位差；ω为电网角频率； ϕn为谐波电流的相位角。在APF系统补偿后，电源侧剩余的补偿电流为：

由式（4）可以得出，APF在工作后，电源侧的谐波及无功电流分量并没有完全补偿，仍然存在与被补偿电流同频率，幅值为原来的2sin（θ/2），相位超前原来ψ1=（π-θ）/2的无功电流分量和幅值，为原来的2sin（θn/2），相位超前原来电流ψn=（π-θn）/2的谐波电流分量。其详细的电流相量示意图如图2所示。

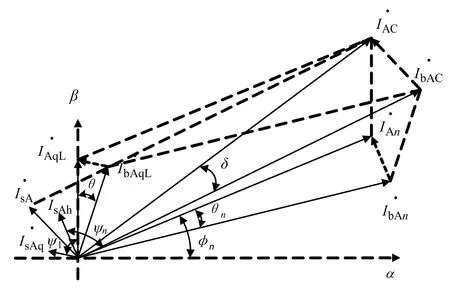
图2 补偿电流相位滞后相量示意图

由此可知，当装置补偿输出电流的相位滞后程度δ越小，电源中剩余的补偿电流就越少；当相位差θ、 θn均为0时，δ为0，也为0。因此，当有源电力滤波器中补偿点与检测点的电流相位不同步时，系统不但没有完全补偿电源中的谐波和无功电流反而形成了新的分量所以，在APF的设计过程中，研究快速准确地补偿电流提取算法和优良的功率调节控制策略，不但能提高其动态性和稳定性，而且也减小了补偿输出电流与电源分量的相位差，从而降低了相位滞后给装置性能带来的不良影响。

2.2 相位滞后仿真分析

在相位滞后仿真分析过程中，假设影响电流相位的各条件均为理想状态，如驱动信号中未加死区时间、功率开关管开通、关断时间为零等。理想状态下的仿真结果如图3所示，其中图3a从上至下为A相负载电流、电源电流及补偿输出电流波形；图3b为负载侧和电源侧电流相应的电流畸变谐波含量柱状图。从图中可以看出，理想状态下APF系统负载电流谐波畸变率为THD25.68%=，系统补偿后，总的谐波畸变率降低到THD1.85%=，各次谐波得到了很好补偿。当补偿电流相位滞后理想状态δ=1°48′，按照工频50 Hz换算成时间，即时间延迟理想状态为100 μs时，仿真结果如图4所示。可以看到，相位滞后情况下的电源侧电流有明显畸变，谐波含量增高达到THD6.72%=，各次谐波未得到有效补偿。由此可以看出，有源电力滤波器的补偿性能和效率对补偿输出电流的相位比较敏感，一旦电流相位有偏差，就会较大幅度的降低系统补偿效果。

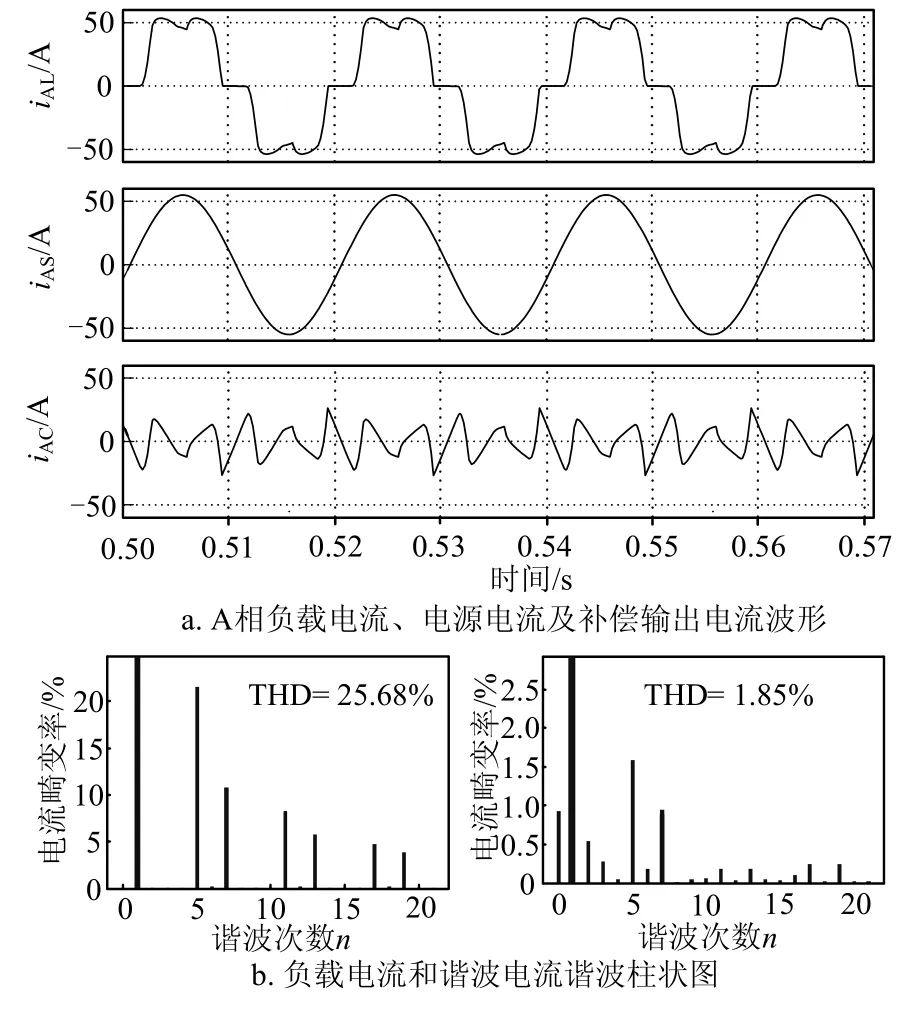
图3 补偿电流相位未滞后时仿真结果

图4 补偿电流相位滞后时电源电流波形及谐波柱状图

2.3 电流相位滞后补偿策略

为避免补偿输出电流相位滞后给有源电力滤波器补偿性能带来的不利影响，提出了一种补偿输出电流零相位滞后（δ=0）的方法，即利用跟踪微分器对提取的给定基准信号相位做相应的超前校正。跟踪微分器对噪声信号放大有很好的抑制效果，可以避免数字信号处理中的高频颤振，相比普通微分器具有较好的性能。

跟踪微分器的状态方程［12-13］为：

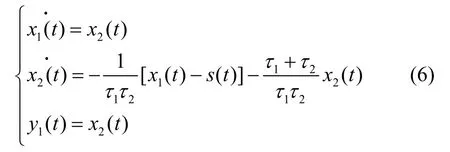
对其进一步离散化得：

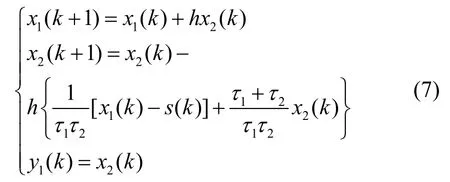
式中， s（t）为输入信号； x1（t）、 x2（t）为中间状态信号； y1（t）为输出信号； τ1、 τ2为时间常数；h为积分步长； x（k）为函数 （x）t在k×h时刻的值； y1（k）是输入信号跟踪微分处理后的信号。运用跟踪微分器实现相位超前校正功能的原理框图如图5所示。

图5 相位超前校正功能框图

由图5可得最后实现相位超前校正的离散化方程为：

式中，λ为预报步长数；r为输出幅值调整度。原始输入信号s首先经过跟踪微分器，得到中间状态信号x1和 x2。 x1频率同原始信号s一致，仅相位有滞后，同时滤除了干扰噪声； x2是 x1经过微分处理后的信号，该信号相位超前于 x1，也超前于原始信号s。相位超前校正主要是利用信号预报的方法来实现，即将滤波后的信号 x1叠加上微分信号 x2与预报步长的乘积共同作为原始信号的无限逼近，达到相位超前校正补偿的效果。

在该补偿系统中，λ取值愈小，意味着超前校正的相位就愈小。因此，通过调整λ值的大小就可以实现可控的相位超前校正补偿。针对图2中补偿电流相位滞后的角度δ，选取适当的时间参数 τ1、τ2和积分步长h，运用仿真的方法确定具体的λ值。在有源电力滤波器具体的应用中，只要使输出电流相位超前值与实际测量的相位滞后相同，就可以实现补偿电流与电源电流谐波及无功分量的相位同步，从而达到补偿性能提高的目的。

对于叠加噪声污染的正弦输入信号s（t）= sin（100πt）+γv（t），其中，（v）t为［-1，1］上的随机噪声，采用跟踪微分器进行相位超前校正测试，当取如表1所示参数时其仿真结果如图6所示。

表1 测试参数

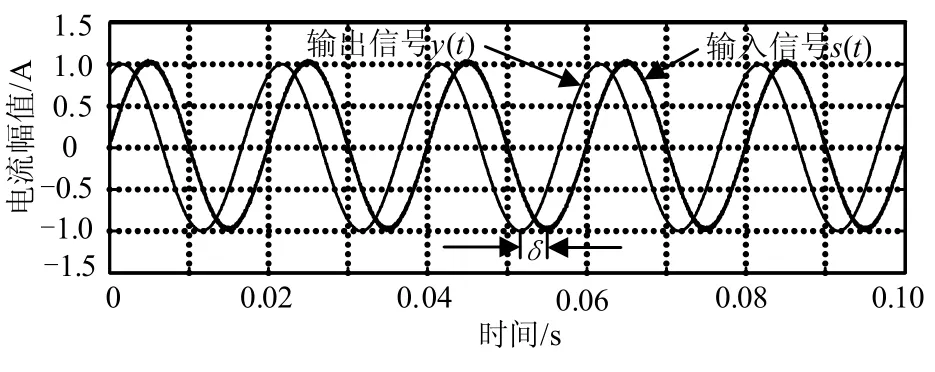
图6 相位超前校正测试结果

由图6可知，信号经过跟踪微分器超前校正后，其幅值和频率没有发生任何变化，而相位产生了超前，同时噪声信号被大部分滤除。因此，若将该方法应用到有源电力滤波器设计中，既可以滤除一部分高频开关噪声，又可以对补偿输出电流的相位进行超前校正补偿，提高有源电力滤波器的补偿性能。

3 MATLAB仿真研究

为验证本文补偿方法的有效性，对并联型三相三线制有源电力滤波器进行了仿真研究。在仿真模型中，非线性负载为三相不控整流桥阻感负载，谐波提取算法采用基于瞬时无功理论的时域法，主功率调节方法为三角波比较控制法［14-15］。为了使仿真条件和效果更接近真实，驱动信号中增加了死区时间，同时设置功率开关管为非理想。系统未应用相位补偿时仿真结果如图7所示，主要的仿真参数如表2所示。

图中可以看出，图7a的三相电源电压波形光滑且稳定，谐波畸变率很小；而图7b的电源侧电流波形由运行补偿前的类方波变为图7c的运行补偿后的近似正弦波形，此时电源侧的电流波形有尖刺，含有部分未除净的谐波分量；图7d为系统输出的三相补偿电流。对电源电流进一步进行FFT分析，可得补偿前的电源电流畸变率为THD28.51%=，图7e所示；APF系统补偿后，电源侧的电流畸变率为THD5.87%=，图7f所示，此时谐波电流滤除率仅为79.4%，谐波滤除效果一般。运用本文的相位滞后补偿方法后（其他条件不变），仿真得到的电源电流波形和相应的电流畸变谐波含量柱状图如图8所示。

表2 APF主要仿真参数

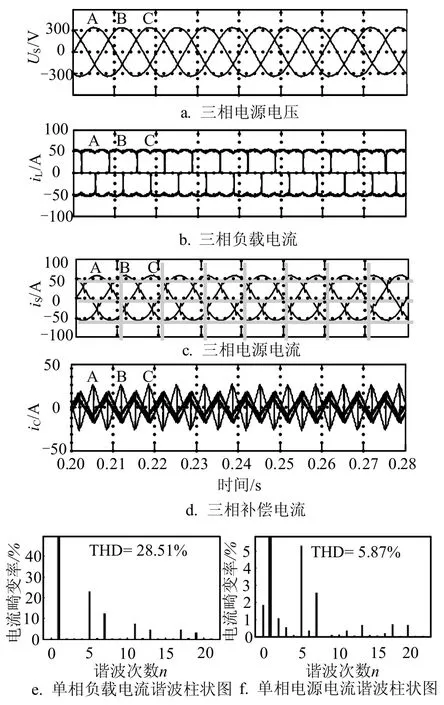
图7 APF正常工作时仿真结果

图8 应用相位补偿后，电源侧电流波形及谐波含量柱状图

比较图7与图8中的电源侧电流波形可知，应用跟踪微分器相位超前校正补偿后，电源侧电流波形较平滑，系统补偿性能大为提升，各次谐波得到了有效抑制。此时电源侧的电流畸变率为THD1.63%=，总体谐波滤除效率达到了94.3%。

4 实际验证及分析

为进一步验证理论分析与仿真研究的可信性，在研制钻井平台用三相三线制有源电力滤波装置的基础上，对本文的策略进行实验验证。该有源电力滤波器的额定容量为70 kVA，满功率输出电流为100 A。装置不仅可以单独补偿无功或谐波电流，也可以根据不同需求将二者按比例同时补偿。

有源电力滤波器正常运行时的实际波形如图9所示，其中图9a、图9b分别为三相系统中A相负载电流、电源电流波形及其相应的电流畸变谐波含量柱状图。由图可知，负载侧电流约为25 A，其电流谐波畸变率为THD24.5%=，主要的谐波有5、7、11、13、17、19次等。APF补偿输出后，电源侧电流谐波畸变率降低为7.1%。此时，有源电力滤波器的谐波电流滤除效率不高，仅为71%，电源中仍然含有较多未补偿的谐波分量。

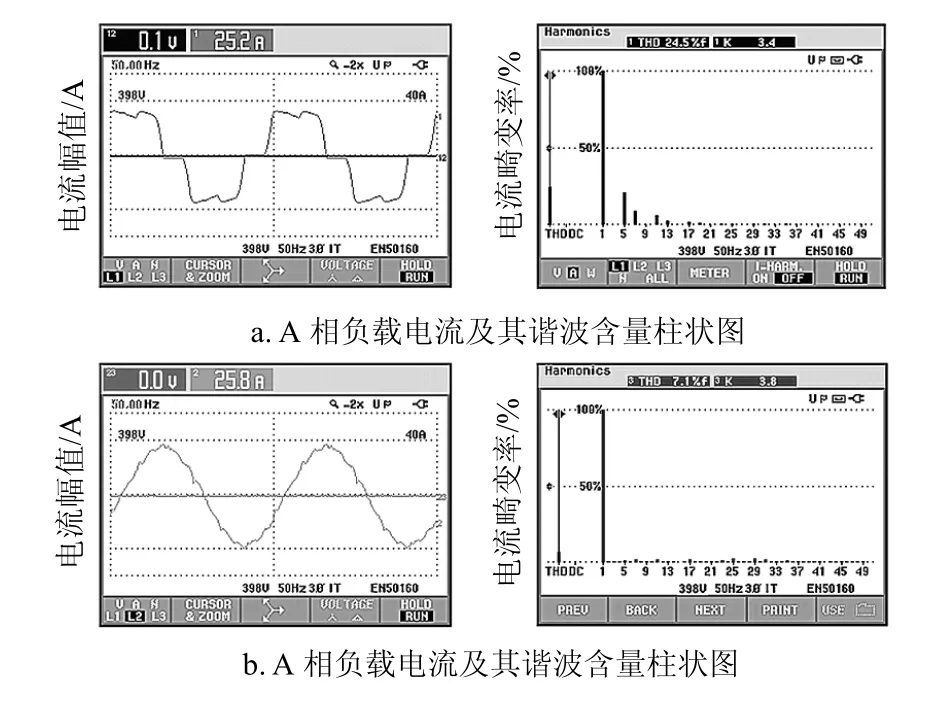
图9 正常情况下，APF系统实际运行波形

运用本文的相位补偿方法对给定电流基准信号进行相位超前校正后，系统运行时关键波形如图10所示。图10中，电源侧电流波形相比图9中较为光滑，毛刺变少，此时电源电流畸变率为3.3%，各次谐波得到进一步抑制，提高了装置补偿性能。

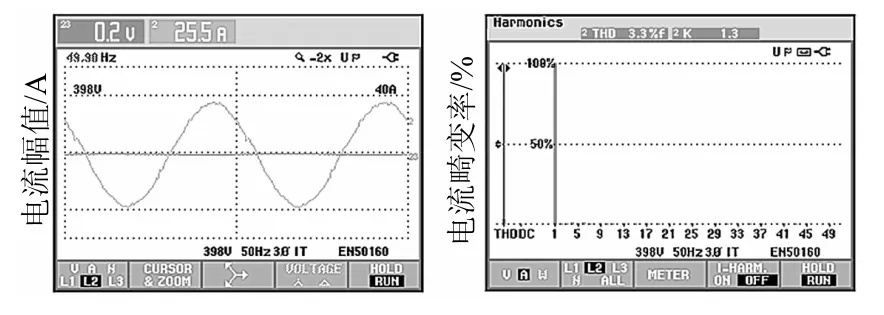
图10 相位超前校正补偿后，电源电流波形及谐波含量柱状图

因此，对有源电力滤波器的补偿输出电流相位进行相应超前校正补偿后，其补偿性能相比之前有较大提高，验证了前述理论分析的正确性和可行性。

5 结 论

本文针对有源电力滤波器对补偿电流的高实时性要求这一特点，研究了一种并联型三相三线制APF补偿性能提高的方法，主要从系统补偿输出电流相比电源电流的相位滞后方面，探讨了其对补偿性能的影响。分析了APF补偿输出电流相位滞后的主要原因，建立并仿真了电流相位滞后数学模型对系统补偿性能的不良影响；提出了补偿电流零相位滞后的超前校正补偿方法。通过仿真和实际工程应用的双重验证，证明了该方法的有效性和可行性，同时为其他类型和不同应用的有源电力滤波器在提高补偿性能和效率方面提供了一定的参考价值。

［1］ 王兆安， 杨君， 刘进军， 等. 谐波抑制和无功功率补偿［M］. 第2版. 北京： 机械工业出社， 2006： 12-24. WANG Zhao-an， YANG Jun， LIU Jin-jun， et al. Harmonic suppression and reactive power compensation［M］. 2nd ed. Beijing： China Machine Press， 2006： 12-24.

［2］ AKAGI H. New trends in active filters for power conditioning［J］. IEEE Transactions on Industry Applications，1996， 32（6）： 1312-1322.

［3］ 罗萍， 王曾. CCM下新型前置功率因数校正电路分析与设计［J］. 电子科技大学学报， 2012， 41（4）： 611-616. LUO Ping， WANG Zeng. Analysis and design of a novel circuit for PFC pre-regulating in continuous current mode［J］. Journal of University of Electronic Science and Technology of China， 2012， 41（4）： 611-616.

［4］ MOHAMED A， SHERIF Z， OSAMA M. Improved active power filter performance based on an indirect current control technique［J］. Journal of Power Electronics， 2011，11（6）： 931-937.

［5］ 尹春杰， 张承慧， 陈阿莲， 等. 基于瞬时电流直接控制的有源电力滤波器电流跟踪新方法［J］. 电工技术学报， 2012，27（4）： 117-122. YIN Chun-jie， ZHANG Cheng-hui， CHEN A-lian， et al. A novel current tracking method for active power filter based on direct transient current control［J］. Transactions of China Electrotechnical Society， 2012， 27（4）： 117-122.

［6］ 赵培洪， 王红星， 平殿发， 等. 时相调制的陷波滤波技术研究［J］. 电子科技大学学报， 2014， 43（4）： 508-513. ZHAO Pei-hong， WANG Hong-xing， PING Dian-fa， et al. Study on notch filter technology of time-phase modulation［J］. Journal of University of Electronic Science and Technology of China， 2014， 43（4）： 508-513.

［7］ CHANG G W， SHEE T. A novel reference compensation current strategy for shunt active power filter control［J］. IEEE Transactions on Power Delivery， 2004， 19（4）：1751-1758.

［8］ 吴敬兵， 罗安， 杨晓峰， 等. 混合有源电力滤波器的新型迭代学习控制［J］. 电网技术， 2011， 35（8）： 104-108. WU Jing-bing， LUO An， YANG Xiao-feng， et al. Novel iterative learning control for hybrid active power filter［J］. Power System Technology， 2011， 35（8）： 104-108.

［9］ 曾令全， 白志亮， 曾德俊， 等. 基于自适应神经网络的有源电力滤波器谐波电流提取方法［J］. 电力自动化设备，2010， 30（2）： 33-37. ZENG Ling-quan， BAI Zhi-liang， ZENG De-jun， et al. Harmonic detection based on adaptive neural network for active power filter［J］. Electric Power Automation Equipment， 2010， 30（2）： 33-37.

［10］ 郭鑫. 独立电源系统有源滤波技术及应用研究［D］. 北京：北京航空航天大学， 2012. GUO Xin. Active power filter technology and applied research of independent electrical power systems［D］. Beijing： Beijing University of Aeronautics and Astronautics， 2012.

［11］ HERRERA R S， SALMERN P， KIM H. Instantaneous reactive power theory applied to active power filter compensation： different approaches， assessment and experimental results［J］. IEEE Transactions on Industrial Electronics， 2008， 55（1）： 163-172.

［12］ 武利强， 林浩， 韩京清. 跟踪微分器滤波性能研究［J］.系统仿真学报， 2004，16（4）： 651-670. WU Li-qiang， LIN Hao， HAN Jing-qing. Study of tracking differentiator on filtering［J］. Journal of System Simulation，2004， 16（4）： 651-670.

［13］ 韩京清， 袁露林. 跟踪-微分器的离散形式［J］. 系统科学与数学， 1999， 19（3）： 268-273. HAN Jin-qing， YUAN Lu-lin. The discrete form of tracking-differentiator［J］. Journal of Systems Science and Mathematical Sciences， 1999， 19（3）： 268-273.

［14］ UYYURU K R， MISHRA M K. An optimization-based algorithm for shunt active filter under distorted supply voltages［J］. IEEE Transactions on Power Electronics， 2009，24（5）： 1223-1232.

［15］ TRINH Q N， LEE H H. An advanced current control strategy for three-phase shunt active power filters［J］. IEEE Transactions on Industrial Electronics， 2013， 60（12）：5400-5410.

编 辑 漆 蓉

Research on PBearf soerdm oann Pche aIsme-pLraogv eCmoemnpt eonf sAactitoivne Power Filter

ZHU Chao-wen1， YUAN Hai-wen1， GUO Xin1， MA Zhao2， and ZHOU Li-mei2
（1. School of Automation Science and Electrical Engineering， Beihang University Haidian Beijing 100191；2. China Electric Power Research Institute Haidian Beijing 100192）

The reasons of the compensation current phase-lag of active power filters （APFs） is analyzed in detail， the corresponding mathematical model is set up， and the phase-lag to influence of compensation performance is described as well by MATLAB. After then， a lead correction method of compensation current with zero phase-lag is proposed to implement the phase synchronization of supply source components. The simulation and actual application results show the feasibility and validity of the proposed method.

active power filter （APF）； harmonics； lead correction； performance； phase-lag

TM712

A

10.3969/j.issn.1001-0548.2016.02.014

2015 - 10 - 29；

2016 - 02 - 29

国家自然科学基金（61273165）；航空科学基金（2014ZD51047）；国家电网公司科技项目（EPRIPDKJ（2014）2863）

朱朝文（1987 - ），男，博士生，主要从事检测技术及自动化装置、嵌入式测控方面的研究.