城际动车组车体模态灵敏度分析

贾尚帅，李明高，张军

(1.中车唐山机车车辆有限公司 产品技术研究中心，河北 唐山 063035；2.大连交通大学 交通运输工程学院，辽宁 大连 116028)*



城际动车组车体模态灵敏度分析

贾尚帅1，李明高1，张军2

(1.中车唐山机车车辆有限公司 产品技术研究中心，河北 唐山 063035；2.大连交通大学 交通运输工程学院，辽宁 大连 116028)*

建立了某城际动车组车体有限单元模型，计算了车体模态，得到了车体模态频率及振型.用数值微分法计算了车体模态频率对车体结构参数的灵敏度，计算结果表明车体前三阶模态频率对底架、侧墙、顶板壳厚度的灵敏度为正值，即车体模态频率随着这些板件厚度的增加而增大；前三阶模态频率对车体端墙和牵枕缓部位结构厚度灵敏度为负值，即车体模态频率随这些板件厚度的增加而减小.在保持车体重量基本保持不变的前提下，用灵敏度信息对车体结构进行修改，使车体前三阶模态频率均得到了提高.

动车组；有限元法；灵敏度；模态频率

0 引言

车体是构成车辆的最重要大型复杂结构之一，承载车辆的全部静载荷和运行中的动载荷，车体结构模态对车辆的动力学性能和车辆乘坐舒适性有很大影响[1-3].车体模态频率是车体最重要的动力学参数，车体模态需要满足相关要求，铁道行业标准“机车车辆动力学性能抬架试验方法(TB/T 3115 2005)”要求整备车体弹性体一阶弯曲模态频率不低于10 Hz，并且要求该频率值与构架浮沉、点头自振频率之比大于1.4，以防止车体弹性体模态与转向架刚体模态发生耦合共振[4-5].在设计过程中在车体减重的同时可能导致车辆模态频率降低或者导致局部振动加大，这需要修改车体结构使其模态频率满足要求.

车体结构修改需要结构灵敏度，结构灵敏度为结构修改提供定量的修改信息，对提高设计效率和设计水平很有意义[6].由于问题的复杂性，在车体结构设计过程中还没有对车体进行广泛的灵敏度分析.文献[7]基于车体一阶垂弯频率的近似计算式推导出了一阶垂弯模态频率对设计变量的灵敏度，并结合应力灵敏度实现了铝合金车体的轻量化设计；文献[8]以动车组地板结构为研究对象，分析了结构的振动响应及其灵敏度.

本文针对某城际动车组车体模态频率较低问题，建立了车体有限单元模型，计算分析了车体前4阶模态，用数值微分法计算了车体模态频率对车体主要板件厚度的灵敏度，基于灵敏度对车体进行修改提高了车体模态频率.

1 结构模态分析基本理论

模态分析的目的是得到结构或者系统的模态频率和振型，振动频率用来分析系统是否与激励频率发生共振，振型可以判断分析结构或者系统哪些位置振动较大、刚度较低.在车体结构设计过程中，也要用有限单元法计算车体自由模态，有限单元法是广泛使用的数值方法.车体结构经过有限单元法离散后，可以得到用矩阵表示的车体自由振动微分方程，一般表示为[8]

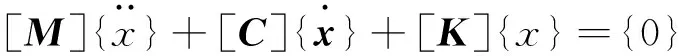
(1)

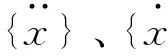
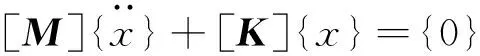
(2)

车体自由振动为简谐振动，可设{x}={X}eiωt，{X}为车体振型向量，ω为方程(2)的特征值，为车体自由振动角频率；代入式(2)，得车体振动的特征方程为

(3)

求解式(3)可以得到车体各阶模态对应的特征值ωi和振型向量{X}i，则车体第i阶自由模态振动频率为fi=ωi/2π.

2 模态频率灵敏度

模态频率灵敏度是车体模态频率随车体结构参数的变化率，灵敏度是结构优化设计过程中需要的重要参数，为结构修改提供修改方向.式(3)对设计变量xj求导数，得

(2)

式(2)左乘{φi}T，由式(1)得下式

(3)

由式(2)、(3)得模态频率灵敏度为

(4)

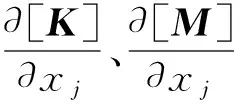
3 车体有限单元模型及模态分析

3.1 参数化有限单元模型

车体共划分493 721个有限单元，采用三角形和四边形单元，以四边形单元为主，单元边长约为50mm.总体和局部有限单元模型如图1所示.

(a) 总体有限单元模型

(b) 局部有限单元模型

3.2 模态计算

前4阶模态频率列于表1.模态计算用整车模型，前3阶模态振型如图2所示.

表1 前4阶模态频率表

该车铝合金车体一阶垂弯模态频率为14.85Hz,小于17 Hz的要求,需要通过结构修改使其提高,以满足相关要求.车体1阶、2阶、3阶模态振型如图2所示.

(a) 一阶菱形

(b) 一阶垂弯

(c) 一阶扭转

4 模态灵敏度

4.1 设计变量

设计变量以重量大于0.98 kN的部件厚度为设计变量，重量小于0.98 kN的部件对车体性能影响相对较小.重量大于0.98 kN的部件主要分布在车体底架、侧墙、车顶、底架边梁等位置，如图3所示，图3中部件名称后面的数字即为设计变量序号，由于厚度不同，同一部件内可能分成几个

设计变量，如侧墙内板包括设计变量14、16、18、19、20.设计变量具体位置如表2所示.

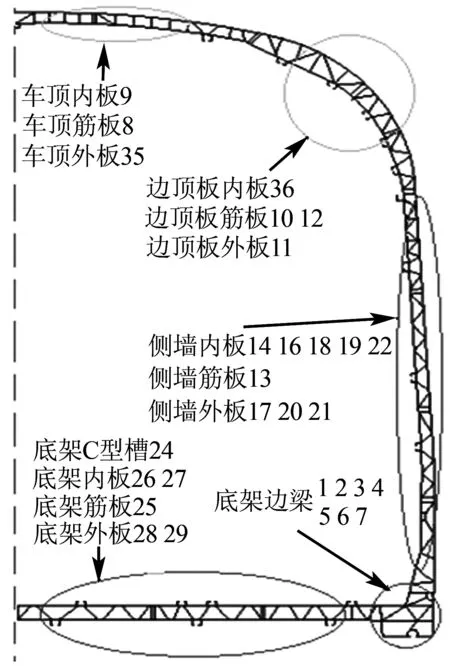
图3 主要设计变量位置

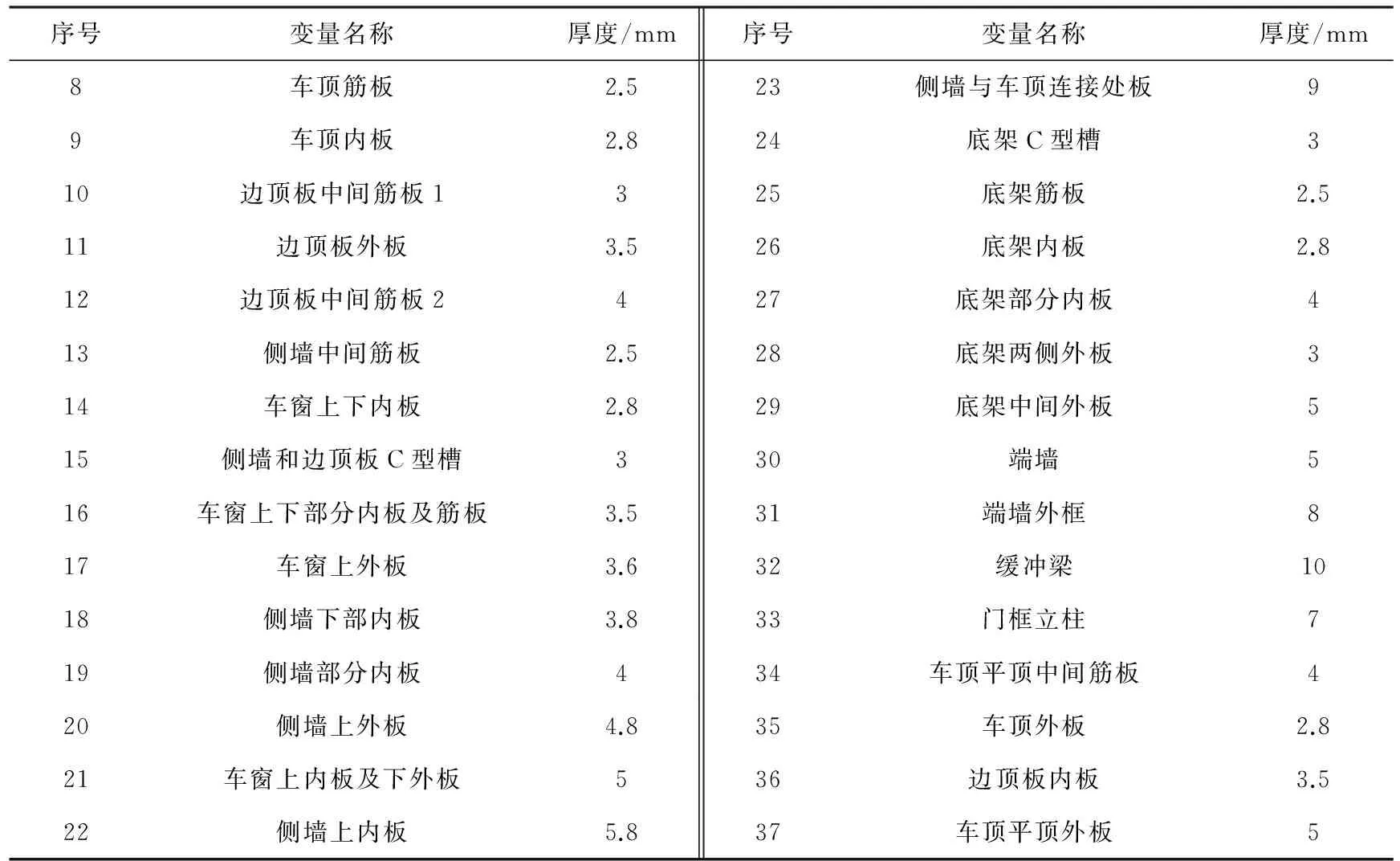
序号变量名称厚度/mm序号变量名称厚度/mm8车顶筋板2.523侧墙与车顶连接处板99车顶内板2.824底架C型槽310边顶板中间筋板1325底架筋板2.511边顶板外板3.526底架内板2.812边顶板中间筋板2427底架部分内板413侧墙中间筋板2.528底架两侧外板314车窗上下内板2.829底架中间外板515侧墙和边顶板C型槽330端墙516车窗上下部分内板及筋板3.531端墙外框817车窗上外板3.632缓冲梁1018侧墙下部内板3.833门框立柱719侧墙部分内板434车顶平顶中间筋板420侧墙上外板4.835车顶外板2.821车窗上内板及下外板536边顶板内板3.522侧墙上内板5.837车顶平顶外板5

4.2 灵敏度计算结果及分析

1、2、3、4阶模态频率对各设计变量的灵敏度分别如图4～图7所示.以下各图中横坐标为设计变量，纵坐标为模态频率灵敏度，灵敏度如果大于零表明模态频率随设计变量的增加而增大，小于零表明模态频率随设计变量的减小而减小. 图4表明，1阶菱形模态频率对设计变量8、9、14、26、35灵敏度较大，对设计变量8即车顶内部筋板的灵敏度最大，对设计变量10、13、15、25的灵敏度为负值，即1阶模态频率随着这些板件厚度的增加而减小.

第2阶模态频率(1阶垂弯)对各设计变量的灵敏度如图5所示，图5表明1阶垂弯模态频率对设计变量14最大，最大值达到0.1 Hz/mm；对设计变量25为负的最大值，其值达到了-0.167 Hz/mm.总体来看，1阶垂弯模态频率对车顶、侧墙、边顶板变量灵敏度为正值，即一阶垂弯随着这些部位板件厚度的增加而增加，对底架内部筋板、底架外板、端墙、缓冲梁部位板件厚度灵敏度为负值.

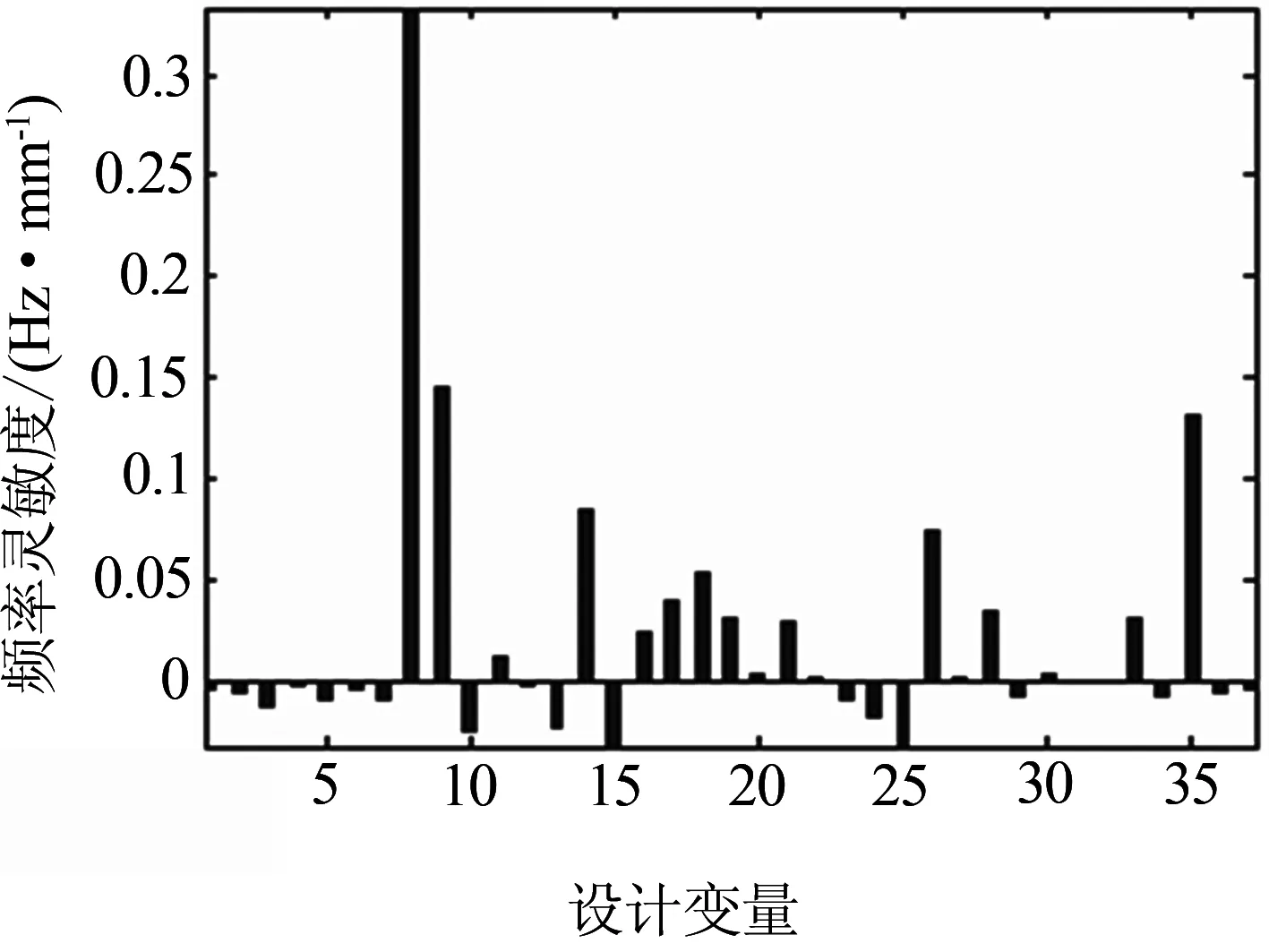
图4 1阶模态频率灵敏度

图5 2阶模态频率灵敏度

3阶模态为1阶扭转，图6表明1阶扭转模态对设计变量14、17灵敏度较大，对设计变量25、10、30等出现较大负值.总体来看，1阶扭转模态频率随侧墙板件厚度的增加而增大，随底架筋板、端墙、缓冲梁板件厚度的增加而减小.

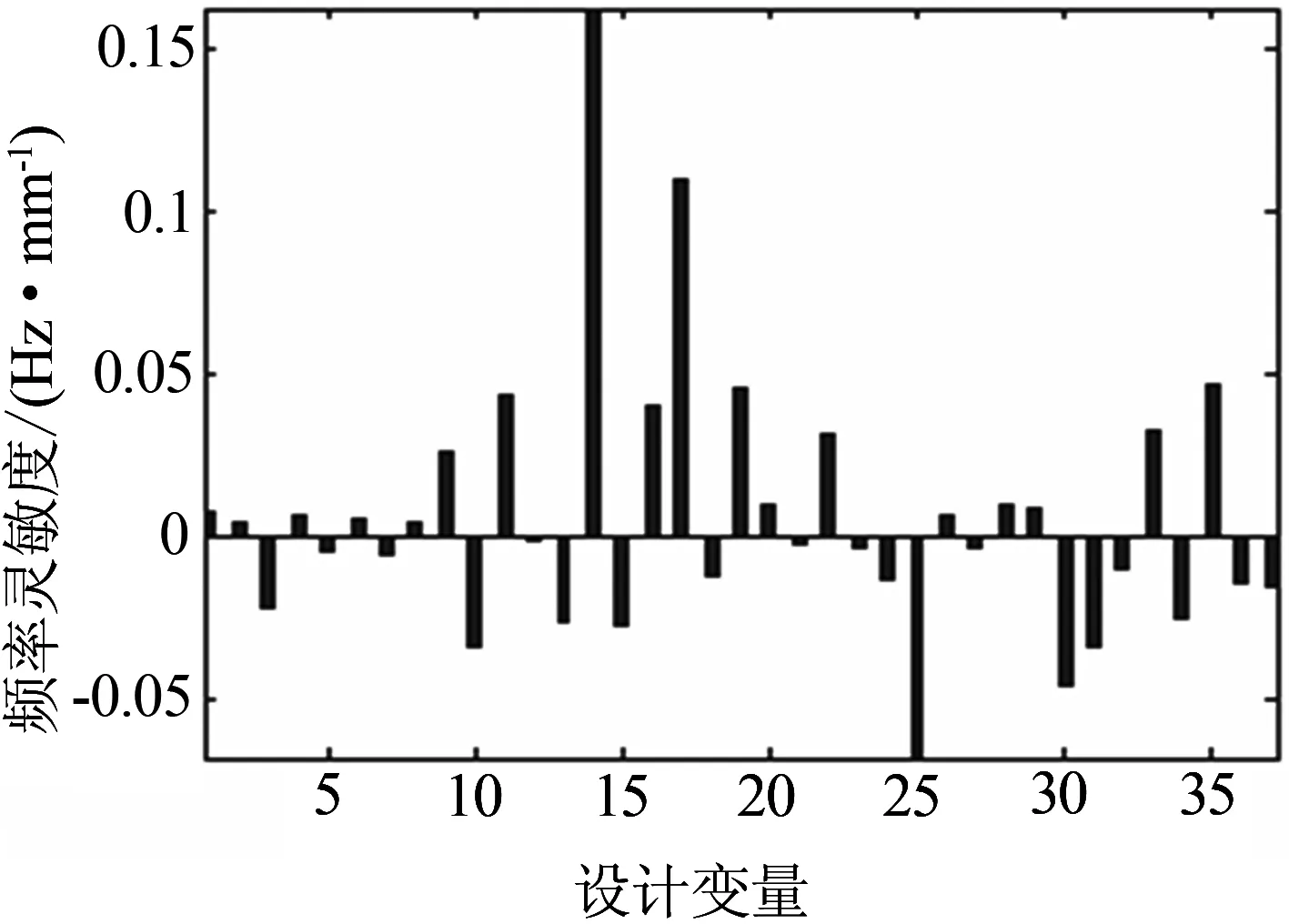
图6 3阶模态频率灵敏度

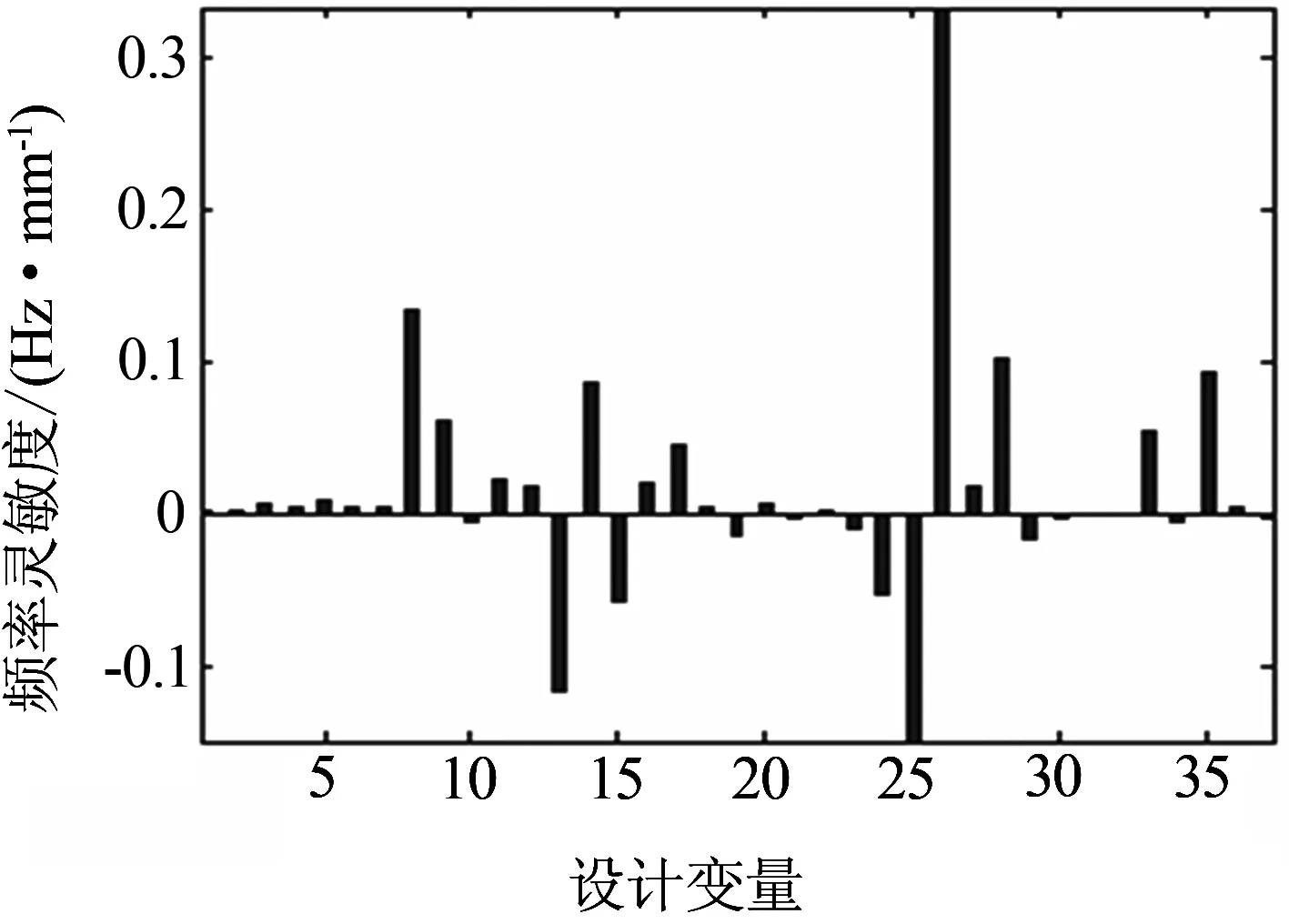
图7 4阶模态频率灵敏度

4阶模态为1 阶呼吸(图7)，该阶模态对设计变量8、14、26、28、35灵敏度为较大的正值，对设计变量26灵敏度最大；对设计变量13、25出现较大负值.

总体来看，各阶模态频率对底架边梁各设计变量均较小；对车顶及边顶板的灵敏度基本为较大的正值，对侧墙各设计变量大多数为较大正值；对端墙、牵引梁较多为负值.除1阶菱形外，各阶模态对设计变量10(边顶板中间筋板)、13(侧墙中间筋板)、15(侧墙和边顶板C型槽)、25(底架筋板)、30(端墙)均为 负值.1阶垂弯模态频率对车顶、侧墙、边顶板、底架变量各设计变量灵敏度均为正值，但对底架设计变量出现较多负值，尤其对底架中间筋板灵敏度达到了-0.15 Hz/mm，即1阶垂弯模态频率会随着底架内部筋板厚度的增加而产生较大的降低.

4.3 车体结构修改及模态分析

通过以上模态灵敏度分析，改变各部件板件厚度，并使车体重量基本保持不变，主要是增加车顶、侧墙、边顶板部位板件厚度，减小底架、端墙部位板件厚度，使前3阶模态频率均得到了提高，1阶垂弯模态频率提高了0.22 Hz，取得了较好的提高车体模态频率效果，但仍没有达到大于17 Hz的要求.研究表明要进一步提高车体模态频率需要对车体的总体结构进行修改，紧紧通过修改壳厚度不能实现使车体模态频率达到大于17 Hz的要求.修改后车体模态频率如表3所示.

表3 修改后车体模态频率 Hz

5 结论

本文建立了某城际动车组铝合金车体车有限单元模型，计算了车体模态，计算分析了车体前4阶模态及模态频率灵敏度，得到如下结论：

(1)前3阶模态频率对车顶、边顶板、侧墙的灵敏度均为正值，即随着这些部位板间厚度的增加模态频率增加；

(2)1、3、4阶模态频率对边顶板中间筋板、侧墙中间筋板、底架筋板、端墙部位灵敏度均为负值；

(3)2阶模态即1阶垂弯模态频率对底架内部筋板、底架外板、端墙和牵引梁部位的灵敏度为负值，即减小这些部位的厚度可以提高1阶垂弯模态频率；

(4)通过灵敏度可以快速对车体结构进行修改，在提高车体模态频率的同时可以保持车体重量相对不变，极大地提高了设计效率和精度；

(5)虽然根据灵敏度可以快速实现对车体结构的修改提高车体性能，但分析表明该城际动车组车体很难通过仅修改各部位壳厚度使车体模态满足相关要求，应对车体截面等总体尺寸进行修改以进一步提高车体模态频率等相关性能.

[1]平学成,王先亮,朱韶光 等. B型地铁铝合金车体工作模态分析[J].铁道机车车辆, 2015, 35(1): 115-117.

[2]王国军,王锴,岳译新. B 型地铁铝合金车体模态优化设计[J].电力机车与城轨车辆, 2012, 35(6):31-33.

[3]吴丹,商跃进,王红 等. 160km/h轨道车车体模态和稳定性有限元分析[J]. 机车电传动, 2011,5: 14-16.

[4]宫岛,周劲松,孙文静 等. 铁道车辆弹性车体垂向运行平稳性最优控制[J]. 同济大学学报, 2011, 39(3):416-420.

[5]罗光兵,曾 京. 基于弹性结构的轨道车辆振动分析[J]. 机械设计与制造,2013(5):67-73.

[6]丁莉芬，缪龙秀. 基于灵敏度分析的结构动力修改方法研究[J].铁道学报, 1999,21(4):17-19.

[7]谢素明,闫雪冬,兆文忠. 基于敏度信息的铝型材高速车体轻量化研究[J].铁道学报,2004, 26(3):26-30.

[8]帅仁忠,赵艳菊,孙召进.高速列车车体型材的结构灵敏度分析研 究[J].铁道机车车辆, 2015, 35(5): 88-90.

Research on Modal Sensitivity of Intercity EMU Bodywork

JIA Shangshuai1, LI Minggao1, ZHANG Jun2

(1. CRRC Tangshan Railway Vehicle Co., Ltd, Tangshan 0630356,China; 2. School of Traffic and Transportation Engineering, Dalian Jiaotong University, Dalian 116028, China)

A finite element model of a intercity EMU bodywork is established, the bodywork modals are extracted, and the modal frequencies are achieved for the first four. Then, the modal frequency sensitivities with respect to the plate thicknesses are calculated by using of numerical differentiation method. The results show that the sensitivity values of the first three modal frequencies with respect to the bottom plates , side wall and top plate are positive, which means that the first three modal frequencies is increased with rising plate thickness. While the sensitivity values of the first three modal frequencies with respect to plate thickness of end wall and traction pillow are negative, which means that the first three modal frequencies is decreased with rising plate thickness. Based on the modal sensitivities, the first three modal frequencies of bodywork have been successfully improved by structure modification, but the weight of the EMU bodywork is not increased.

EMU bodywork; finite element method; sensitivity; modal frequency

1673-9590(2016)04-0024-05

2015-12-15

中国铁路总公司科技研究开发计划资助项目(2014J004-O)；牵引动力国家重点实验室开放课题(TPL1402)

贾尚帅(1982-)，男，工程师，博士，主要从事车辆结构优化设计的研究E-mail: jiashangshuai@tangche.com.

A