应用马尔科夫模型分析潜孔钻机的可靠性

张逸轩，戴晓江，王孝东，毕春杰，何 波

（1.昆明理工大学 国土资源工程学院，云南 昆明 650093；2. 云南省公路开发有限公司 ，云南 昆明 650032；3. 西藏华泰龙矿业开发有限公司，西藏 拉萨 850200）

科 技

应用马尔科夫模型分析潜孔钻机的可靠性

张逸轩1，戴晓江1，王孝东1，毕春杰2，何 波3

（1.昆明理工大学 国土资源工程学院，云南 昆明 650093；2. 云南省公路开发有限公司 ，云南 昆明 650032；3. 西藏华泰龙矿业开发有限公司，西藏 拉萨 850200）

基于Isograph软件，根据潜孔钻机特性，结合马尔科夫模型对潜孔钻机进行了可靠性分析，建立了潜孔钻机的分析模型，推导出潜孔钻机的可靠性计算公式。带入实例数据进行可靠性计算，且对比分析是否加入维修状态的两种计算结果。发现设备的等待工作对设备的使用效率有很大影响；要提高可用度，降低故障率，提高维修率是有效途径；推进提升机构的故障对于潜孔钻机的可靠性影响较大。

潜孔钻机；马尔科夫模型；Isograph软件；可用度

潜孔钻机在生产中主要用于矿山的钻凿爆破，是矿山企业生产能力的重要支撑［1］，例如柿竹园多金属矿用连续阶段崩落法开采490 m以上富矿段，采用YQ-100型潜孔钻机在凿岩硐室内凿水平扇形炮孔［2］等。因此钻机的可靠性密切关系着矿山的生产。由于矿山企业的发展现状较为粗犷，导致基于可靠性的维修管理方案很难发展，这方面研究还不够受重视［3-4］。长期以来，矿山设备可靠性的研究方向大多是进行FMECA、FTA分析［5-7］，但所得指标并未考虑设备的维修。本文拟以矿山设备中的KQ-200型钻机为例，结合设备维修情况，借助可靠性分析软件Isograph建立马尔科夫分析模型，对设备正常工作状态以及故障状态之间的转移情况进行分析，获得加入维修状态的设备可靠性情况。

1 马尔科夫过程

1.1 基本思想

马尔科夫过程是针对具有无后效性的可修复系统的一种随机过程，是研究某一个状态和另外一个状态之间转移关系的一个随机模型。设随机过程｛X（t），t∈T｝，其中：时间T=｛0，1，…｝，状态空间I=｛0，1，2，…｝，若对任一时刻n，以及任意状态i0，i1，…，in-1，i，j，有P｛X（n+1）=j|X（n）=i，X（n-1）=in-1，…X（1）=i1，X（0）=i0｝=P｛X（n+ 1）=j|X（n）=i｝，则称：｛X（t），t∈T｝为一个马尔科夫链。运用马尔科夫链模型进行计算可以得到系统在各个可能状态的状态概率，并进一步求出其他的系统可靠性指标。

1.2 潜孔钻机可靠性评估特点

潜孔钻机系统属于可修复的系统，设备出现故障是随机的，通常由正常工作状态转向出现故障的状态，经维修又返回正常的工作状态，以此不断往复循环。这种状态之间的转移完全是随机的。在马尔科夫过程中，分析的系统根据转移概率在各状态间进行转移，未来某个时间的状态是不确定的，这同设备的使用状态很相似，所以可以采取马尔科夫方法对设备进行可靠性分析。

2 基于Isograph软件的马尔科夫模型

2.1 状态划分

潜孔钻机使用过程中出现的状态是建立马尔科夫模型的基础。潜孔钻机设备投入生产运行后，作为统计对象随即进入正常工作状态，再根据设备的使用情况，设备的使用状态总体可以分为正常状态和故障状态两种状态［6］，根据分析，建立潜孔钻机在使用过程中的各个状态的全态模型如图1所示。

2.2 Isograph软件的Markov模块

马尔科夫过程主要是用来分析例如可修复系统这种在连续时间变化下具有离散状态的随机过程。

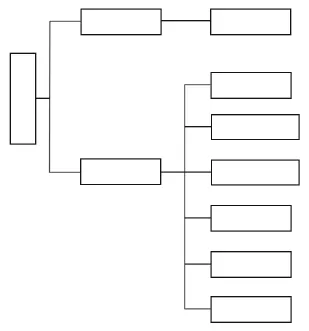
图1 潜孔钻机全状态模型

Isograph软件Markov模块使用马尔可夫过程分析方法，建立系统状态转移图，以计算系统在连续时间和离散状态下的可靠性和可用性。

2.3 马尔科夫模型的建立

2.3.1 模型的建立

通过对潜孔钻机设备的使用状态进行分析，找出了潜孔钻机设备在使用过程中主要出现的状态，分别是运转、钻具、回转供风机构、推进提升机构、钻架、机架、行走机构。潜孔钻机的马尔科夫模型中出现的状态，运转状态表示在此状态下设备无故障发生，设备在生产计划内正常工作；故障状态表示此状态下设备有故障发生并对故障维修，设备不能正常运行，除运转状态外，设备的某一故障部位发生故障则设备进入故障状态。在使用过程中，由于故障的发生，会导致设备由一种状态转向另外一种状态，由运转状态转向故障状态中的某一个状态，潜孔钻机设备故障马尔科夫状态转移图如图3所示。

设备的运行时间里含有等待时间，也就是说设备除运转和故障两种状态之外，还应该有一个等待工作的状态，根据对设备现场的使用时间分析，等待工作状态表示待修、待活的使用时间状态。所以潜孔钻机的马尔科夫状态转移关系会如图4所示。

图3为潜孔钻机加入等待工作状态的马尔科夫状态转移图，为了区分只考虑两种状态的马尔科夫模型，将该状态转移关系定义为设备的3种状态的马尔科夫模型，将只考虑正常和故障两种状态的状态转移关系定义为设备的两状态的马尔科夫模型。

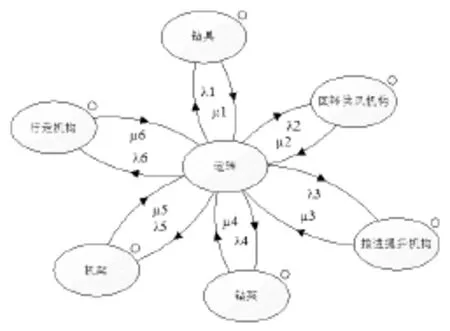
图2 钻机设备的状态转移图

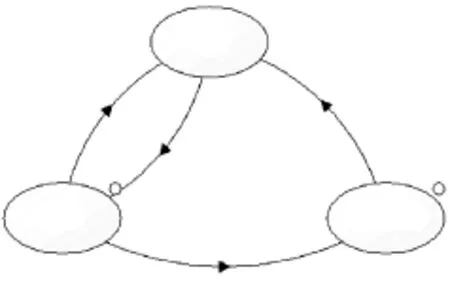
图3 设备实际状态转移

2.3.2 模型的计算过程

设设备处于正常运转状态下的概率为p0，处于故障状态的各个状态的概率为pi（i = 1，2，3，4，5，6），状态之间的转移概率分别是λi和μi（i = 1，2，3，4，5，6）。设运转状态为状态0，可能发生故障的部位钻具、回转供风机构、推进提升机构、钻架、机架、行走机构为6个状态依次为状态1、状态2、状态3、状态4、状态5、状态6。根据马尔科夫过程的推导公式：

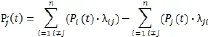
其中表示状态j转移至状态i的概率，表示可靠性模型在时间t状态j的概率。

基于马尔科夫模型钻机设备可靠性的求解并把其转换成矩阵的形式，就可以得到查普曼-柯尔莫戈洛夫方程：

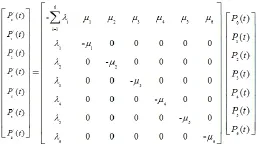
其中：

用拉普拉斯变换对查普曼—柯尔莫戈洛夫方程求解：

然后运用拉普拉斯反变换对Pi（S）求解，就得到了设备的可靠性模型在时间t状态i的概率，就是设备在t时刻的可用度。

2.4 软件计算结果分析

2.4.1 模型的赋值计算

根据收集到的潜孔钻机设备多年故障维修记录进行统计整理分析，分析得到设备两状态之间的转移概率如表1所示。用所得到的状态转移概率对Isograph软件建立的潜孔钻机设备马尔科夫可靠性模型进行赋值，分析潜孔钻机的可靠性。

表1 钻机设备的故障率和修复率

设备3种状态之间的状态转移概率如表2所示。

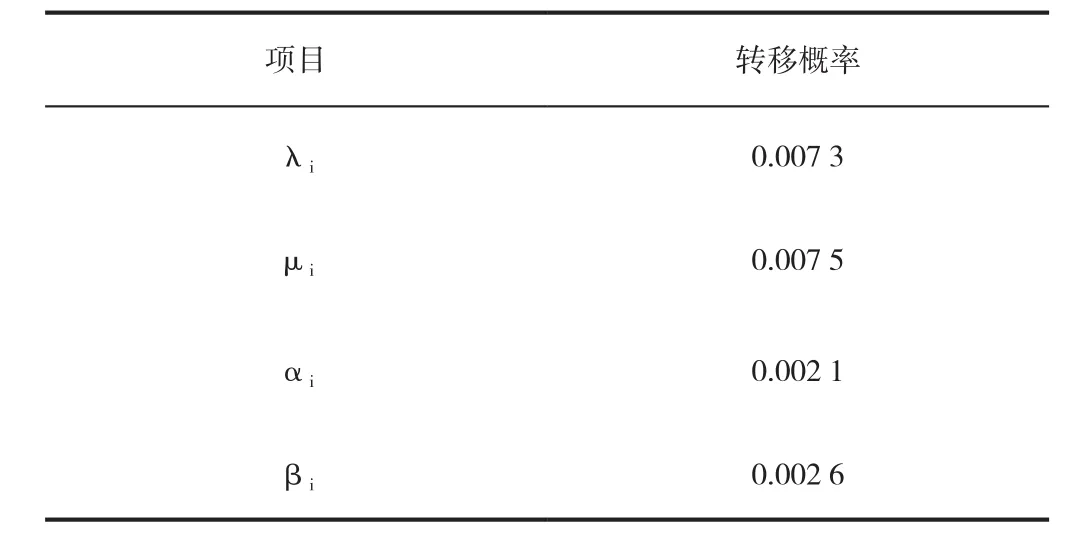
表2 设备三状态之间的转移概率

2.4.2 计算结果分析

设备的可用度是考虑设备故障到正常再从正常到故障的可修复系统的可靠性量值，是其稳态可用度。根据以上各表中数据，对建立的马尔科夫模型进行赋值，当t足够大时，经Isograph软件计算得潜孔钻机的稳态可用度，可用度为0.580 4，不可用度为0.4196。从计算结果可知潜孔钻机的可用度还有一定的提升空间。对加入等待工作状态的马尔科夫模型进行计算，得到考虑等待工作的马尔科夫模型稳态可用度，可用度为0.473 7，不可用度为0.526 3。

经对比，发现考虑等待状态的设备可用度有所降低，说明设备的等待工作将影响设备的使用效率。设备的可用度计算，考虑了设备的状态转移，即当设备出现故障处于停运状态时，经过维修使设备恢复到正常生产状态，所以设备的可用度偏低可能就是由于故障导致正常状态向故障状态的转移率较高，或者是因为设备故障状态向正常状态的转移率较低。因此降低设备的故障率或提高设备的维修效率有助于提升设备的可用度。

2.4.3 设备可用度变化分析

经Isograph软件对马尔科夫模型进行赋值计算，软件还可以得到潜孔钻机的可用度变化曲线，以钻机为例如图4所示。根据图4钻机设备的可用度变化曲线可以看出，设备在投入运行后，设备的可用度随时间的增加而逐渐降低，刚开始的阶段设备的可用度随时间变化较大，最后随时间的增加而慢慢趋于稳定。

计算得到的可用度是在考虑设备的在故障状态下经维修转向正常运转状态转移过程下得到的数值，如果不考虑设备状态之间的转移，即维修过程，设备的可用度会如图5所示，从图中可以看出设备的可

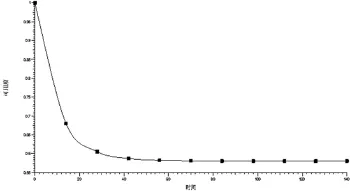
图4 考虑维修过程钻机的可用度变化曲线

图5 未考虑维修过程钻机的可用度变化曲线

用度会随着时间增加逐渐的降低，但并不随着时间的持续增加而会趋于一个相对稳定的值，由此得出，维修对设备可靠性有着重要影响。

3 结 论

本文根据潜孔钻机特点，建立了马尔科夫数学模型。通过计算以及结果分析，得出以下结论。

1）仅考虑到故障和正常状态时设备的可用度为0.580 4。当加入等待工作状态时，设备的可用度为0.473 7。发现考虑等待状态的设备可用度有所降低，说明设备的等待工作对设备的使用效率有很大影响。

2）从文中可用度计算公式可知，设备的可用度偏低是由于故障导致正常状态向故障状态的转移率较高，或是设备故障状态向正常状态的转移率较低。因而要提高可用度，降低故障率率，提高维修率是有效途径；

3）根据收集到数据的整理分析，对比各部件对潜孔钻机的可靠性影响得知，推进提升机构的故障对于潜孔钻机的可靠性影响较大，因而要加强对推进提升机构的故障检修。

［1］ 陈龙. 潜孔钻机的结构设计及性能分析［D］. 西安： 长安大学， 2015.

［2］ 郑磊， 余斌， 胡建军， 等. 中国钨矿采矿技术现状分析［J］. 有色金属（矿山部分）， 2013， 65（1）： 12-15.

［3］ 刘玉锋. 潜孔钻机运动学仿真与整机稳定性分析［D］. 西安： 长安大学，2015.

［4］ 陈晓辉. 地下铀矿山运输提升系统可靠性研究［D］. 衡阳： 南华大学，2015.

［5］ 毕春杰， 戴晓江， 秦清华. 基于Isograph的FMECA分析在潜孔钻机中的应用［J］. 煤矿机械， 2015， 36（4）： 309-312.

［6］ 廖瑞金， 肖中男， 巩晶， 等. 应用马尔科夫模型评估电力变压器可靠性［J］. 高电压技术， 2010， 36（2）： 322-328.

［7］ 穆宜敏. 基于全寿命周期的掘进机可靠性工程平台建设［D］. 太原： 太原理工大学， 2015.

M arkov M odel for Reliability Assessment of DTH Drill

ZHANG Yixuan1，DAI Xiaojiang1，WANG Xiaodong1，BI Chunjie2，HE Bo3
（1. Faculty of Land Resource Engineering of Kunming University of science and technology，Kunming Yunnan 650093，China；2.Construction Group of Yunnan Highway Development and Investment Co. Ltd，Kunming Yunnan 650032，China；3.Tibet Huatailong Mining Development Co. Ltd，Lasa xizang 850200，China）

In order to analyze the DTH drill reliability and research on the equipment maintenance management. Based on the Isograph software，according to the characteristics of DTH drill and combined w ith the Markov process to analyze the reliability of DTH drill and build a mathematical analysis model for it.Taking the instance data into the model and comparing of the calculations whether to join the state of repair. Conclusions:The waiting time of equipment has great infuence on the eff ciency； To improve the availability and reduce the fault rate， improving the rate of repair is an effective way； The fault of Push-lifting-Mechanism has a great effect on the reliability of DTH drill.

DTH Drill；Markov model；Isograph；Availability

TD231.6

A

10.14101/j.cnki.issn.1002-4336.2016.03.037

2016-06-21

中国博士后科学基金项目（2015M582763XB）

张逸轩（1990-），男，山西太原人，硕士研究生，研究方向：安全系统工程技术研究，手机：18468085570，E-mail：1253197520@qq.com；通信作者：戴晓江（1957-），男，云南昆明人，副教授，硕士研究生导师，研究方向：数字矿山，手机：13888337152，E-mail：981350458@qq.com.