一种船舶操纵水动力导数的计算方法

吴兴亚，高霄鹏

(海军工程大学 舰船工程系，武汉 430033)



【基础理论与应用研究】

一种船舶操纵水动力导数的计算方法

吴兴亚，高霄鹏

(海军工程大学 舰船工程系，武汉 430033)

以船舶操纵性预报为研究背景，针对某一民用打捞船型，基于CFD方法，借助STAR-CCM+平台，运用RANS方程及VOF算法，对船模进行数值模拟PMM试验，考虑航行中自由液面兴波和船模姿态变化，设计了船模按纯横荡运动及某固定频率下艏摇运动的船舶操纵水动力导数求解方法，并以采用回归方程求得的结果作为依据与数值计算结果相印证，表明所求水动力导数的有效性以及求解方法的可行性。

操纵运动方程； 水动力导数；CFD； STAR-CCM+； PMM试验

船舶操纵水动力导数的求取通常包括约束模型试验法、自航模型试验加系统辨识法、数据库(回归公式)估算法及数值计算法。其中各种方法利弊共存，约束模型试验精度较好，但花费高且周期长，船模与实船之间存在着尺度效应。近年不断开发应用自航模型试验加系统辨识法，目前已出现利用神经网络、最小二乘、卡尔曼滤波等系统辨识法预报水动力导数。文献[1-2]基于RBF网络和BP神经网络对船舶操纵水动力导数进行了计算分析研究，Abkowitz基于卡尔曼滤波(extended kalman filter,EKF)辨识方法，对Esso Osaka 油轮的操纵性进行了试验结果分析，得出了较为理想的系统辨识结果。近年，相关学者又通过建立系列数据库对船舶设计初始阶段的水动力进行估算[3-8]，因其对新船型无法进行相应计算存在相当大的局限性；随着计算机科学技术的飞速发展和计算流体力学(CFD)技术对船舶水动力操纵性能的精确预报，利用商用流体力学软件的再次开发计算水动力导数成为一种有效方法，文献[9]即借助FLUENT的二次开发对相关水动力导数进行了数值仿真计算。

本文以船舶操纵性预报为研究背景，采用CFD这一先进工具，通过在STAR-CCM+软件平台[10]上对船模进行PMM运动试验，求解部分水动力导数，并通过与回归公式[11]求解得出的相应结果进行印证，表明本文基于船舶作纯横荡运动求解线加速度导数以及较优简谐振荡频率下纯艏摇运动求解相应水动力导数的计算方法具有一定可行性和有效性，对今后船舶操纵性的快速预报具有一定的指导意义。

1 数值计算方法

1.1 控制方程

在数值模拟船体周围流场时，认为水为不可压缩的黏性流体，在流场流动时遵循质量守恒及动量守恒定律，其张量形式下的连续性方程和雷诺平均Navier-stokes(Reynolds-Averaged Navier-stokes,RANS)方程如下：

(1)

(2)

式中：ui为流体平均速度分量；μ为流体动力黏性系数；P为平均压力；ρ为流体质量密度。

1.2 湍流模型

目前在工程中广泛使用两方程式模型，诸如标准k-ε模型、Realizablek-ε模型、标准k-ω模型等。综合考虑各模型适用条件范围，在求解分离和复杂二次流特征流动时，通常采用Realizablek-ε湍流模型进行RANS方程的封闭。Realizablek-ε模型输运方程如下：

(3)

(4)

式中：Gk、Gb为湍流产生项；σk、σε为普朗特数；C1、C1ε为常数；YM为湍流耗散项。

1.3 VOF算法

VOF是一个简单的多项流模型，通过VOF算法中VOF波设定，在三维情况下，使船模适用于6自由度的一种运动模型。VOF算法作为一种处理自由面的有效方法，求解原理是根据各个时刻流体在网格单元中体积的变动量与网格单元自身体积的比值函数F来构造、追踪自由面，从而确定自由面的形状和位置。当在某时刻网格单元中比值函数F=1时，说明该时刻状态下网格单元均被指定相的流体充满，当F=0时，说明该单元被另一相流体充满。F函数满足方程：

(5)

1.4 STAR-CCM+仿真平台及应用

STAR-CCM+采用连续介质力学数值技术和最新的IT和CFD技术，通过稳健准确的数值算法、覆盖面宽广的物理模型以及易处理的网格体系进行物理情况的准确模拟计算。应用STAR-CCM+软件仿真平台计算船体在不同运动工况下的水动力是文章的中心工作。在该软件仿真平台上，结合Realizablek-ε湍流模型，利用VOF算法，通过求解RANS方程，对船模在不同工况下的运动进行数值计算模拟，求得船模所受力以及力矩，并通过后期的数据拟合分析得到待求得船舶各水动力导数。

2 数值计算模型

2.1 计算对象

计算船模为一民用打捞船型，缩尺比为1∶18，其三维建模示意图如图1。

图1 计算船模

2.2 计算域

计算域选取如图2所示，围绕船体周围建一个拖曳水池(Towing Tank)，船尾处水线面下0.35m设为坐标原点，在船模上方1.2L(L为船长)处设为上界面，在船模前方、后方各2.4L处分别设为入流界面和出流界面，在船模左右两侧以及下方2.4L处设定壁面。运用布尔运算(Boolean)。将船体与水池分离，船体表面均设定为无滑移壁面。

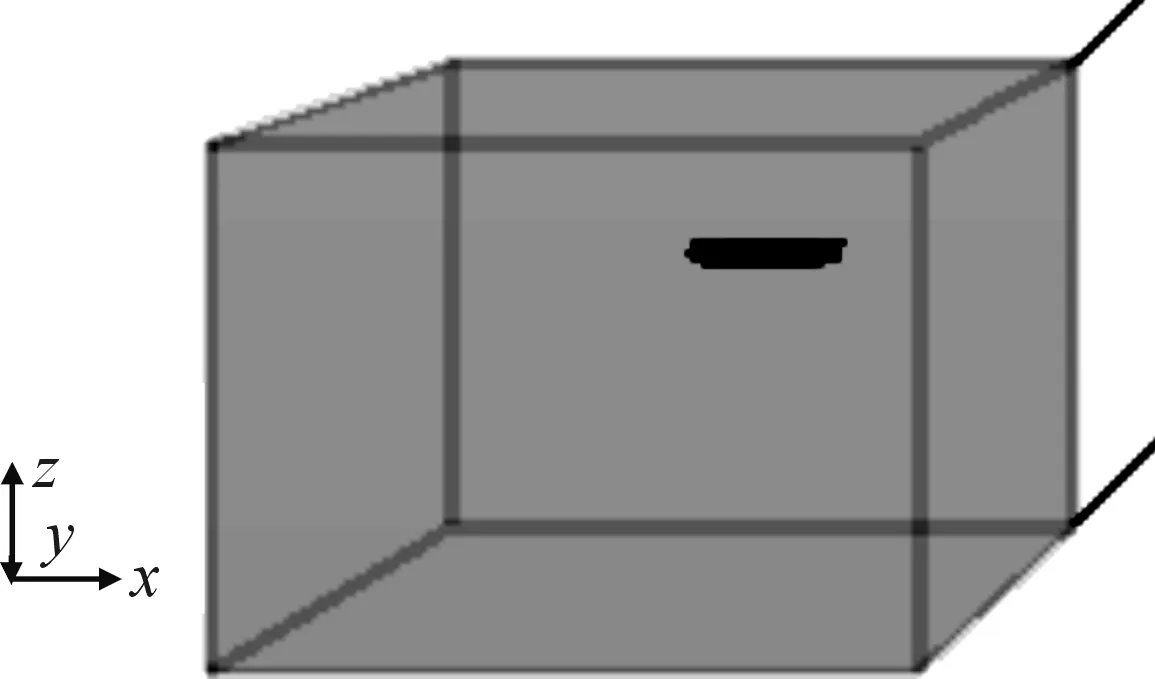
图2 船模计算区域

2.3 计算条件设定

由于船舶实际操纵运动本质为低频运动，满足计算状态。在拖曳水池中，船体自身并不运动，水流以特定流速流向船体，设定边界条件时，将入流界面设为速度入口，出流界面设为压力出口，各壁面均设为无滑移边界。计算模式选用隐式不定常和欧拉多项流，同时利用VOF方法处理船体运动产生的兴波自由面重构等强非线性现象，湍流模式采用K-Epsilon模式。在DFBI中，根据船模特定的运动工况选取不同的运动模式及自由度。

2.4 计算网格划分

控制域网格划分如图3所示，在划分计算域网格时，为保证计算可行性、节约计算时间，在对船模周围较远控制域以及水线面以上船模的网格进行划分时，采用稍微稀疏的网格，同时为保证计算结果的准确度，对水线面、球皮艏处等一些敏感区域进行网格加密处理，保证计算中网格品质。

图3 计算控制域网络划分

3 数值计算结果

3.1 纯横荡运动

3.1.1 运动工况及求解方法介绍

船舶作纯横荡运动如图4所示，艏向角在运动过程中不发生变化，船模在沿纵向匀速运动的同时叠加一个横向低频振荡。通过使船作纯横荡运动，可以确定船舶操纵的位置导数和线加速度导数，其运动方程为：

(6)

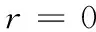
(7)

(8)

(9)

(10)

其中：ψ为艏向角; r为角速度; a为横向简谐振荡运动幅值; ω为简谐运动频率。

图4 纯横荡运动

计算船舶纯横荡运动时，取固定横荡幅值，振荡频率依次取为0.06 Hz、0.08 Hz、0.10 Hz、0.12 Hz和0.14 Hz 5种工况，分别依次计算每种工况下船模受到的水动力。船模作纯横荡运动时，考虑船模作小振幅振荡。在线性假设下，船模在随船坐标系下水动力方程可表示为：

(11)

(12)

将式(11)、式(12)中的各参数项无因次化，得到无量纲化水动力表达式为：

Bcosωt+Asinωt

(13)

Ncosωt+Msinωt

(14)

其中：

(15)

(16)

(17)

(18)

通过上述无量纲化水动力表达方程(13)、(14)，将船舶作横荡运动时的受力曲线运用Matlab进行拟合，求得方程(15)～方程(18)中的各系数项A、B、M、N，再通过各系数项的方程表达式，进行二次曲线拟合，求得相应线加速度水动力导数。

3.1.2 计算结果

选取船模在振幅为0.15 m，振荡频率为0.14 Hz工况下时受力曲线如图5，两条曲线均在受力稳定周期内，保证船体受力的稳定性，通过Matlab的曲线拟合功能获得船模受力曲线方程(19)、曲线方程(20)。船模在5种振荡频率下的受力拟合曲线见图6、图7，数值计算结果见表2所示。

图5 受力曲线

拟合曲线方程为：

y=-0.000 838 1sinωt-0.002 552cosωt

(19)

拟合曲线方程为：

y=-0.000 979 7sinωt-0.001 759cosωt

(20)

图6 纯横荡运动水动力导数拟合曲线

图7 纯横荡运动水动力导数拟合曲线

水动力导数YvNv数值计算结果-0.00392-0.00494

3.2 纯艏摇运动

图8为船舶作纯艏摇运动示意图，在运动坐标系下，船舶做纯艏摇运动时，船模在沿纵向方向上匀速运动的同时叠加一个横向方向上低频振荡和艏相角周期性的变动。合速度方向与船舶中纵剖面方向一致，其运动方程可表示为：

(21)

(22)

(23)

(24)

其中：ψ为艏向角；ψ0为艏向角幅值；r为角速度；a为横向简谐运动幅值；ω为简谐运动频率。

经前期数值仿真计算并分析结果得知，船舶作艏摇运动频率取0.05 Hz与0.07 Hz时，其数值仿真结果较接近估算值。故此次艏摇运动仿真实验中频率取为0.06 Hz，振幅依次取0.1、0.3、0.5、0.7和0.8 m，分别计算每种振幅下船舶受的水动力。水动力方程为：

(25)

(26)

将式(25)、式(26)无因次化，与船舶作纯横荡运动处理方法类似，利用Matlab对船舶受力曲线进行拟合求得船模纯艏摇运动时相应水动力导数。计算结果见表3所示。

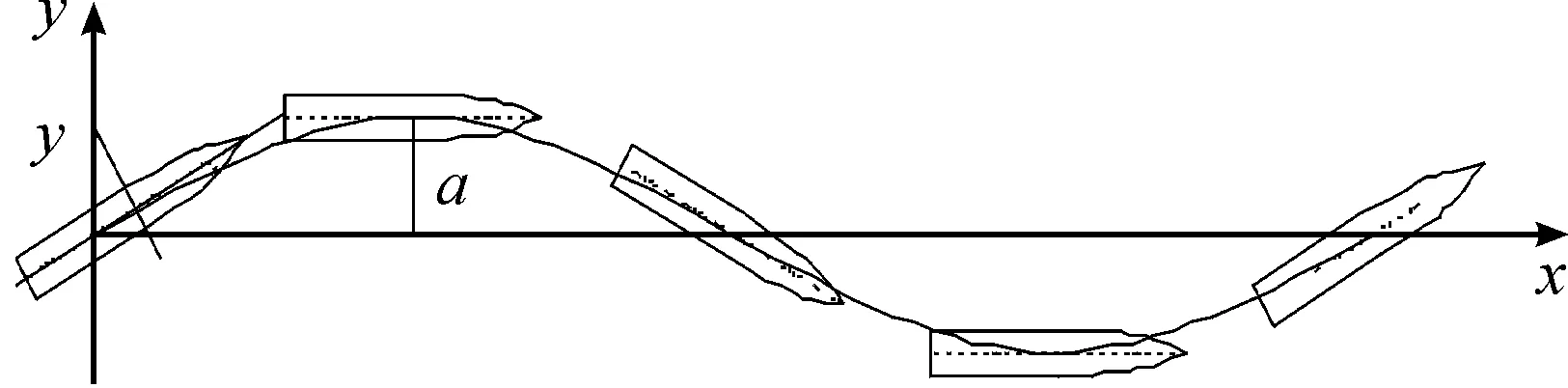
图8 纯艏摇运动

水动力导数数值计算值回归公式估算值Yr'0.003150.003154Nr'-0.00280-0.00221

4 结论

1) 数值计算与采用回归公式计算结果印证，表明基于STAR-CCM+平台进行PMM试验求取线性水动力导数的准确性与可行性。

2) 基于PMM实验使船舶作纯横荡运动求得加速度水动力导数是一种较快速准确估算水动力的方法，具有一定的工程实用价值，为下一步船舶操纵性仿真预报的开展奠定了基础。

[1] 张晓兔,张乐文,刘祖源.基于RBF网络的操纵水动力预报[J].武汉理工大学学报:交通科学与工程版,1999(6):602-604.

[2] 唐晓光,刘祖源.基于神经网络的船舶操纵运动水动力预报[J].武汉理工大学学报:交通科学与工程版,2002,26(1):25-27.

[3] PETERSEN J B,LAURIDSEN B.Prediction of Hydrodynamic Forces From a Database of Maneuvering Derivatives[C]//MAARSIM 2000,International Conference on Marine Simulation and Ship Maneuvering.Orlando,USA,2000.[4] LEE T I,AHN K S.On an Empirical Prediction of Hydrodynamic Coefficients for Modern Ship Hulls[C]//MARSIM’03,International Conference on Marine Simulation and Ship Maneuverability.Kanazawa,Japan,2003.

[5] KIJIMA K,NAKIRI Y.On the Practical Prediction Method for Ship Maneuvering Characteristics[C]//MARSIM`03,International Conference on Marine Simulation and Ship Maneuverability.Kanazawa,Japan,2003.

[6] YOSHIMURA Y,MA N.Maneuvering Prediction of Fishing Vessls[C]//International Conference on Marine Simulation and Ship Maneuverability.Kanazawa,Japan,2003.

[7] KIJIMA K,NAKIRI Y.On the Practical Prediction Method for Ship Maneuverability in Restricted Water[C].Transation of the Wear-Japan Society of Naval Architects,2003(107).

[8] 李冬荔.粘性流场中船舶操纵线性水动力导数计算[C]//黑龙江省造船工程学会学术年会论文集.出版地不详:[出版社不详],2008.

[9] 李冬荔,王彪,杨亮.船舶操纵线性水动力导数计算方法研究[J].中北大学学报(自然科学版),2008,29(06):531-537.

[10]李晓文,林壮,郭志群,等.基于Star-CCM+的滑行艇水动力性能模拟计算[J].中南大学学报(自然科学版),2013(S2):133-137.

[11]范尚雍.船舶操纵性[M].北京：国防工业出版社，1988.

(责任编辑 杨继森)

Calculation Method of Hydrodynamic Derivatives Related to Ship Maneuvering

WU Xing-ya, GAO Xiao-peng

(Department of Naval Architecture Engineering, Naval University of Engineering, Wuhan 430033, China)

Taking the ship maneuverability prediction as the research background, hydrodynamic derivatives related ship maneuvering were analyzed by CFD method for a certain civilian salvage ship, with STAR-CCM+ software platform, using RANS equations and VOF algorithm, and numerical simulation was carried out on the model PMM test, considering the free liquid surface and the attitude of the model change in the process of oblique towing, and the maneuverability hydrodynamic derivative solving methods were designed according to the swaying motions and yawing motions of stationary oscillation modes, and the results of numerical calculation was compared with the results by regression equation, which confirms the effectiveness of the result to solve the hydrodynamic derivatives and the feasibility of solving method.

maneuvering equation; hydrodynamic derivatives; CFD; STAR-CCM+; PMM test

2016-05-24；

2016-06-20

吴兴亚(1992—)，男，硕士，主要从事舰船流体动力性能研究。

10.11809/scbgxb2016.10.038

吴兴亚，高霄鹏.一种船舶操纵水动力导数的计算方法[J].兵器装备工程学报，2016(10):181-184.

format:WU Xing-ya, GAO Xiao-peng.Calculation Method of Hydrodynamic Derivatives Related to Ship Maneuvering[J].Journal of Ordnance Equipment Engineering,2016(10):181-184.

U661.3

A

2096-2304(2016)10-0181-05