多级边坡施工过程引起的影响区面积数值模拟研究

梁华友，周海清，周淑玲，苏 杭，李剑清

(1.后勤工程学院 a.军事土木工程系; b.岩土力学与地质环境保护重庆市重点实验室;

c.国防建筑规划与环境工程系，重庆 401331；

2.总参工程兵第四设计研究院，北京 100850； 3. 68612部队，银川 750000)



【基础理论与应用研究】

多级边坡施工过程引起的影响区面积数值模拟研究

梁华友1a,1b，周海清1a,1b，周淑玲2，苏 杭3，李剑清1c

(1.后勤工程学院 a.军事土木工程系; b.岩土力学与地质环境保护重庆市重点实验室;

c.国防建筑规划与环境工程系，重庆 401331；

2.总参工程兵第四设计研究院，北京 100850； 3. 68612部队，银川 750000)

采用FLAC3D软件对多级边坡施工过程进行系统的数值模拟，结合CAD制图软件求出施工过程所引起的影响区面积，并用函数拟合影响区面积与锚索预加预应力值之间的关系；结果表明：多级边坡施工过程中，本级边坡支护结构在施加锚索预应力时不仅会引起本级边坡坡体产生一定面积的预压区，还会减少下一级边坡开挖引起的坡体松弛区的面积；使用对数函数对多级边坡开挖引起的松弛区面积与上一级支护结构所施加的锚索预应力的关系进行拟合；使用幂函数对支护结构施工引起的预压区面积与该级支护结构所施加的锚索预应力之间的关系进行拟合，得到多级边坡施工过程引起的影响区面积的经验计算公式。计算公式拟合度较高，相关系数R2均大于等于0.958。该公式可以为设计人员确定多级边坡施工影响区面积提供一定的参考依据。

数值模拟； 影响区；预应力

随着我国基础建设的大力推进，在工程实践中面临高边坡开挖支护的问题越来越多。高边坡施工中，人们所关心的核心问题是边坡开挖之后引起的松弛区范围和支护之后引起的预压区范围。只有确定了施工引起的影响区形状和大小，才可以提高滑坡推力计算的准确性，选择合理的工程方案，客观评估边坡的整治效果[1-2]。高边坡一般选用联合支挡结构的支护方式，采用分级开挖分级支护施工。多级边坡施工过程中，本级支护结构的施工不仅能提高本级边坡的稳定性，还能减小下一级边坡开挖引起的松弛区范围，因此设计人员难以确定多级边坡施工过程引起的影响区范围。现在国内外对于高边坡的施工效应研究[3-16]，定义了开挖松弛区以及支护引起的预压区，也探讨了一些确定开挖松弛区范围的方法，对多级边坡施工影响区的形状有一定的研究，但是对于多级边坡施工中影响区面积的计算，目前研究仍然不深入。本文利用FLAC3D软件结合图1所示的多级边坡模型对多级边坡施工过程进行数值模拟研究，使用CAD作图软件作出影响区的边界图，计算各个影响区面积的大小。据此探讨多级边坡在施工过程中各级支挡结构中锚索预应力发生变化时各级边坡影响区面积的变化，寻找锚索预应力与影响区面积的关系，给出两者的经验公式，为设计人员确定多级边坡在施工过程中的影响区面积提供参考依据。

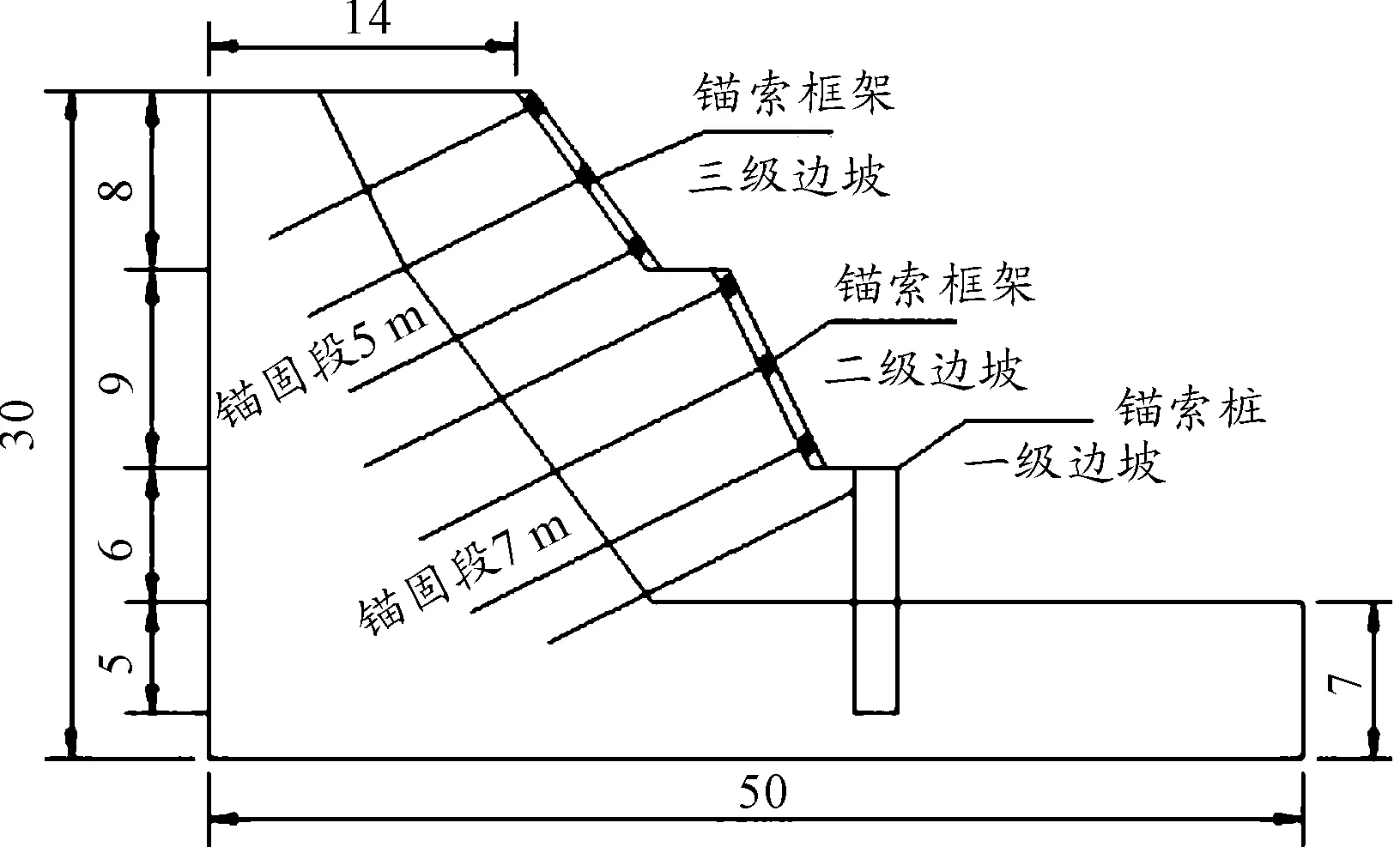
图1 多级边坡模型(单位:m)

1 数值模拟

1.1 数值模型建立

多级边坡的断面如图2所示，图2中①为基岩，②为边坡坡体，②-1，②-2，②-3为边坡开挖的土体。第一次开挖面的坡率为1∶0.75，第二次开挖面的坡率为1∶0.5。

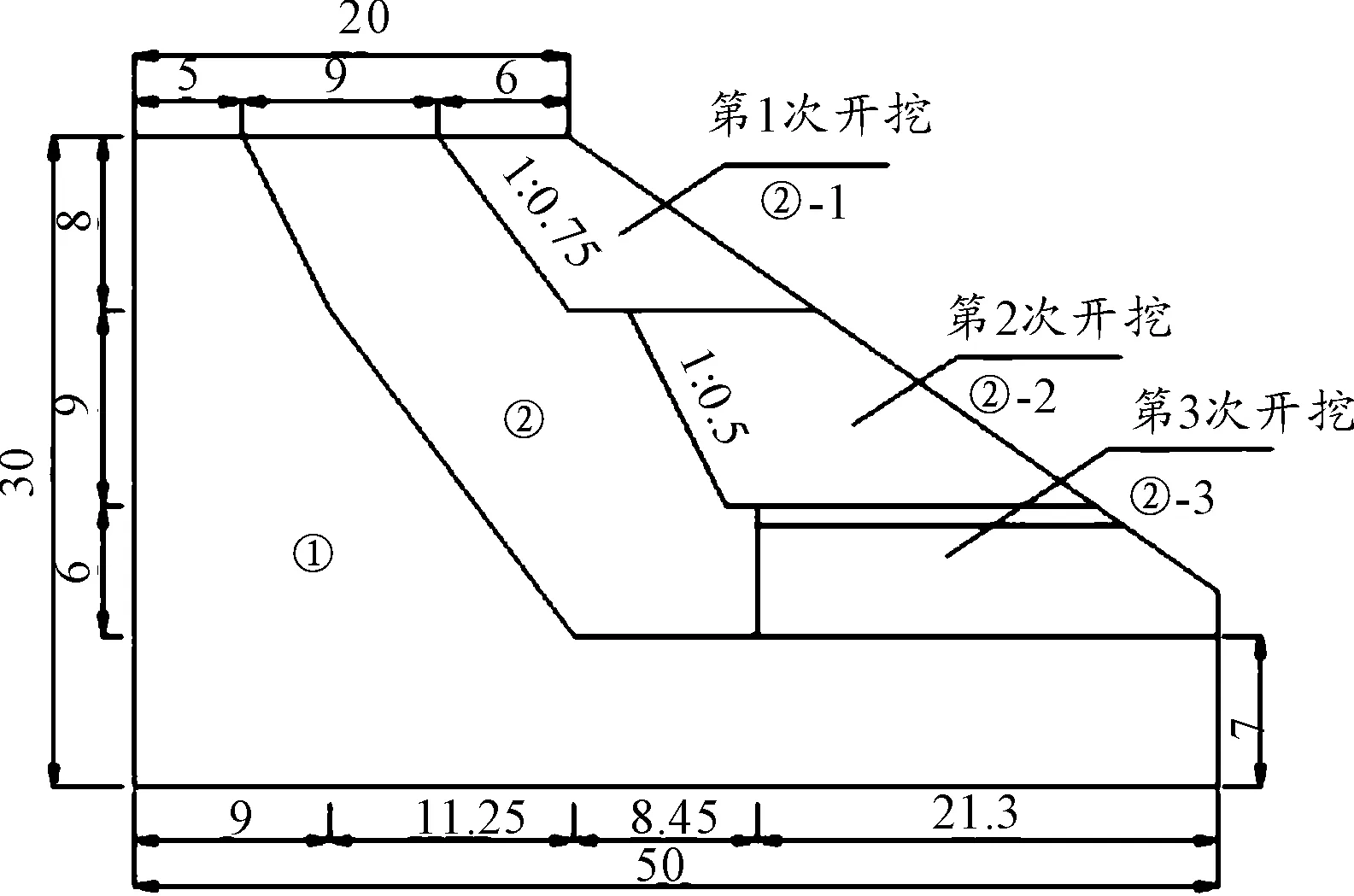
图2 边坡断面示意图(单位:m)

1.2 建立多级边坡三维数值模型

在FLAC3D建立一个横断面如图2所示的三维边坡模型，如图3所示。其中边坡的长宽高分别为：50 m、7 m和30 m，模型网格共划分45 864个实体单元和51 272个节点。在模型底部的平面施加竖向位移约束，在X=0、X=50和Y=0、Y=7的平面施加水平位移约束，Z=30的平面为自由界面。数值模型土体材料的本构模型采用Mohr-Coulomb弹塑性模型，该模型是带有非相关流动法则的弹塑性模型，比较符合边坡的实际情况。基岩的重度为21.5 kN/m3，黏聚力为708 kPa，内摩擦角为31.3°，弹性模量为980 MPa；边坡坡体的重度为17 kN/m3，黏聚力为34.6 kPa，内摩擦角为24.6°，弹性模量为200 MPa。使用FLAC3D的锚索单元和梁单元模拟锚索框架结构；第三级边坡中锚索锚固段长5 m，第二级边坡中锚索锚固段长7 m。使用FLAC3D的锚索单元和桩单元模拟锚索抗滑桩结构，抗滑桩桩身全长11 m，锚固段5 m，锚索的水平倾角均为26°。锚索与框架梁(纵横梁材料参数相同)的计算参数如表1所示，抗滑桩的计算参数如表2所示。

图3 边坡有限元模型

锚索弹性模量/GPa横截面积/m2水泥浆摩擦角/(°)单位长度水泥浆粘结力/(kN·m-1)单位长度水泥浆刚度/GPa水泥外圈周长/m自由段1955.56e-40000锚固段1955.56e-4252.1e30.560.4082框架梁弹性模量/GPa泊松比横截面积/m2y轴惯性矩/m4z轴惯性矩/m4极惯性矩/m4280.20.096.75e-46.75e-41.35e-3

表2 抗滑桩的计算参数

1.3 数值模拟方案

利用FLAC3D软件建立多级边坡三维模型以后，为了方便测量施工影响区的范围，先通过在锚索单元表面注入水泥浆对锚杆进行模拟，在各级边坡中等距离设置4根水平倾角为10°的锚杆。锚杆单元材料的计算参数中的水泥浆刚度、水泥外圈周长等计算参数相对较小，以减少对边坡体变形的影响。锚杆的主要作用为测定影响区的范围，称为量测锚杆[1]。其工作原理以测量坡体松弛区为例，在进行边坡过程中，坡体松弛区内的土体都有向坡面变形的趋势，在量测锚杆表面指向坡面的摩擦力。因此从坡面向坡内方向，量测锚杆的轴力是逐渐累积增加的。如果越过了松弛区边界，进入了量测锚杆的“锚固段”，作用在量测锚杆表面的摩擦力反向，作用于量测锚杆的轴力就会逐渐减小。由于松弛区的边界具有以上特点，就可以通过量测锚杆轴力增长趋势的突变判断该处为边坡松弛区的界线，上下各排量测锚杆所测出的边坡松弛区界线相连，就得到边坡的松弛区范围。测量坡体预压区的方法也一样，只不过作用于量测锚杆表面的摩擦力方向不同。对多级边坡施工过程进行系统的数值模拟，求得各个影响区边界点的坐标信息，在CAD软件中将边界点标出，按顺序将边界点连接起来得到各个影响区的范围，利用CAD软件中的面积计算工具，求得影响区的面积，最后探讨影响区面积的计算公式。

整个施工模拟过程采用“逆作法”，边开挖边支护，多级边坡施工过程可以分为6个工况进行：工况1开挖第三级边坡；工况2采用锚索框架梁对第三级边坡进行支护；工况3开挖第二级边坡；工况4采用锚索框架梁对第二级边坡进行支护；工况5设置抗滑桩和锚索，采用锚索抗滑桩对第一级边坡进行支护；工况6开挖第一级边坡。

2 模拟结果分析

在前期进行了大量数值模拟的基础上，确定各级支挡结构的锚索预应力分别为100，200，300，400，500，800，1 000 kN；对每种工况进行数值模拟时，施加不同锚索预应力值，得到多级边坡施工过程每种工况引起的影响区面积，据此研究施工引起的影响区面积与锚索预应力值的关系。

2.1 第三级边坡开挖预压区面积和该级锚索预应力的关系

对工况2进行数值模拟时，锚索施加不同的初始预应力。根据模拟结果作出第三级边坡在不同预应力作用下的坡体预压区范围，如图4所示。

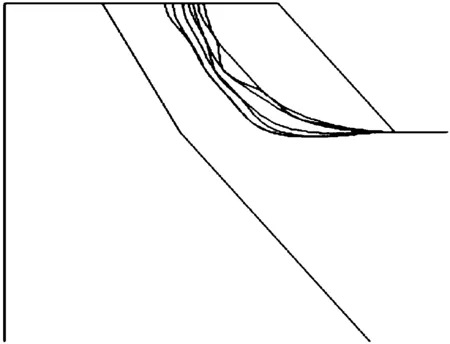
图4 第三级边坡在不同预应力作用下的坡体预压区

从坡面向坡体内部方向，依次是第三级边坡的锚索框架在预应力为1 000，800，500，400，300，200，100 kN完成支护后第三级边坡产生的坡体预压区边界。利用CAD软件计算面积的工具计算各个影响区面积，得到第三级边坡坡体预压区面积与锚索预应力的关系如表3所示。

表3 第三级边坡坡体预压区面积和预应力的关系

从表3可以看出：在一定范围内，随着锚索预应力F1的逐渐增大，坡体预压区的面积A1也呈增大趋势。当锚索初始预应力增加到800 kN及以上时，预压区面积增长趋势逐渐平缓。F1为第一次支护(第三级边坡支护)时的锚索预应力，A1为施工第三级边坡锚索框架并施加锚索预应力时坡体预压区面积，即第三级边坡锚索框架预压区的面积。

将F1作为自变量，A1作为因变量进行拟合来研究两者的内在关系，A1-F1关系的最佳拟合效果分别为二次抛物线型和幂函数型，如图5所示。

考虑边界条件F1=0时，A1=0，三级边坡锚索框架预压区的面积和锚索预应力的关系用幂函数去拟合更加符合实际情况，其经验公式如下所示：

(1)

式(1)中相关系数R2=0.958。数值计算中得到的模拟值和经验公式计算得到的经验值的对比结果见表4。由表4中的相对误差可以看出，根据经验公式所求的预压区面积相对误差较小，在允许误差范围内。

图5 三级边坡坡体预压区面积和预应力关系的拟合效果

预应力F1/kN1002003004005008001000预压区面积A1/m2模拟值35.3938.2640.5546.3448.9853.2153.84经验值33.95339.00242.29744.80146.84651.54653.812相对误差/%4.061.934.313.324.353.290.042

2.2 第二级边坡开挖松弛区面积和第三级边坡锚索预应力的关系

边坡支护不仅能提高本级边坡的稳定性，对于下一级边坡的开挖引起的松弛区范围也会造成一定的影响。图6为第三级边坡支护完成后开挖第二级边坡形成的边坡引起的松弛区范围。其中，从坡面向坡体内部方向依次是第三级边坡锚索框架在预应力为1 000，800，500，400，300，200，100 kN完成支护后开挖第二级边坡产生的坡体松弛区边界。研究发现在保持其他条件不变的情况下，第三级边坡锚索预应力越大，开挖第二级边坡后引起的坡体松弛区范围越小，其对应关系见表5。将F1作为自变量，A2作为因变量进行拟合，研究两者的内在关系，其相应的经验公式如下所示。A2为工况3坡体松弛区面积，即第二级边坡开挖松弛区的面积。

A2=176.52-16.833ln(F1+50)

(2)

式(2)中，相关系数R2=0.980 37。

图6 开挖第二级边坡引起的松弛区

预应力F1/kN1002003004005008001000松弛区面积A2/m292.6483.5179.4371.1169.6963.460.25

若第三级边坡开挖后不支护，则第二级边坡开挖后形成的坡体松弛区如图7所示，此时第二级边坡开挖松弛区面积A2=125.3 m2，即边界条件为F1=0时，A2=125.3 m2。而用式(2)的经验公式计算得到的松弛区面积为A2=110.67 m2，考虑到数值模拟中网格划分、边界条件等的影响，此经验公式较为合理。经过检验，根据经验公式所求的预压区面积相对误差较小，在允许误差范围内。

图7 第三级边坡开挖后不支护进行第二次开挖引起的松弛区

2.3 第二级边坡锚固预压区面积和该级锚索预应力的关系

在第三级边坡中的预应力锚索初始预应力达到800 kN经计算平衡后模拟施工开挖第二级边坡，对第二级边坡锚索框架施加不同的初始预应力以获得不同预压区，此时引起的坡体预压区范围如图8所示。从坡面向坡体内部方向依次是第二级边坡锚索框架在预应力为1 000，800，500，400，300，200，100 kN完成支护时第二级边坡产生的坡体预压区边界。坡体预压区的面积和锚索预应力的关系如表7所示。对比表7和表3发现，在相同的锚索预应力下，第二级边坡锚索框架预压区的面积约为第三级边坡锚索框架预压区的面积的2倍，这是因为第二级边坡与第三级边坡的坡高、坡率、锚索与坡面的夹角以及锚索锚固段的长度不同，说明第二级边坡比第三级边坡的支护效率高。从表7可以看出，第二级边坡锚索框架预压区的面积和锚索预应力呈非线性递增关系。将F2作为自变量，A3作为因变量，对A3-F2关系进行拟合得到经验公式如下。F2为第二次支护(第二级边坡支护)时的锚索初始预应力，A3为工况4坡体预压区面积，即第二级边坡锚索框架预压区的面积。

(3)

式(3)中，相关系数R2=0.981。同时式(3)满足边界条件F2=0时，A3=0，即第二级边坡锚索预应力尚未施加时，在没有其他外力作用的条件下预压区面积为零。经过检验，根据经验公式所求的预压区面积相对误差较小，在允许误差范围内。

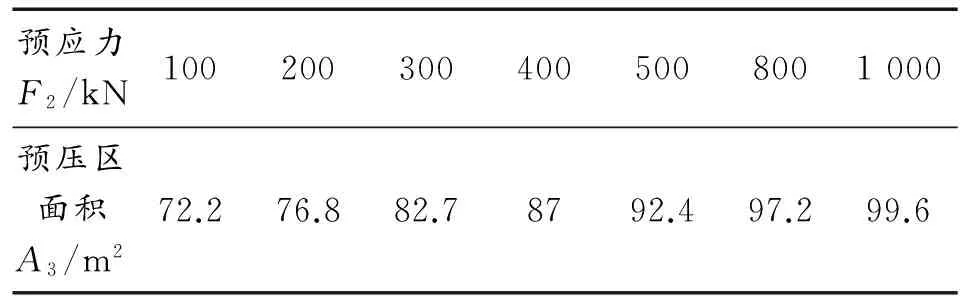
表7 第二级边坡坡体预压区面积和预应力的关系

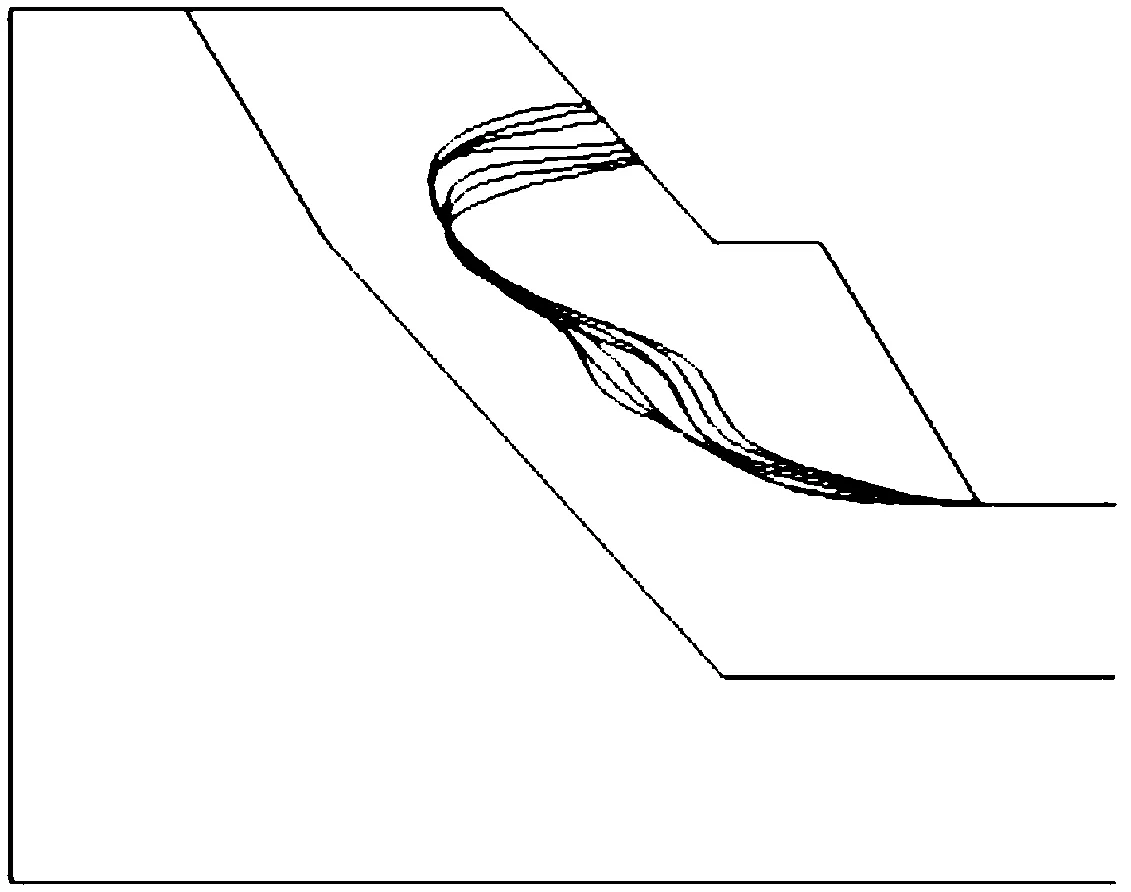
图8 第二级边坡在不同预应力作用下的坡体预压区

2.4 第一级边坡锚固预压区面积与该级锚索预应力的关系

在第二级边坡中的锚索预应力达到800 kN经计算平衡后模拟施工第一级边坡，根据工程实际，对于第一级边坡施工，先施工锚索抗滑桩，锚索抗滑桩施工完成后进行边坡开挖。

根据模拟结果得到施工引起的坡体预压区如图9所示。第一级边坡预压区面积与该级锚索预应力的关系如表8。对比前两级边坡预压区面积可以发现，第一级边坡在相同大小锚索预应力的锚固作用下，预压区面积要小很多，这是因为锚索抗滑桩与锚索框架的作用机制不一样，锚索抗滑桩对边坡进行支护主要是依靠限制土体的侧向变形；而锚索框架则是通过锚索施加巨大预应力于框架上，再通过框架传递于土体，增大滑动面的法向力。同时，第一级边坡土体的固结程度比上两级好，因而预压区的面积相对会小一些。将F3作为自变量，A4作为因变量，对A4-F3关系进行拟合得到经验公式如下。F3为第三次支护(第一级边坡支护)时的锚索初始预应力，A4为工况5坡体预压区面积，即第一级边坡锚索抗滑桩预压区的面积。

(4)

式(4)中，相关系数R2=0.973 2。经过检验，根据经验公式所求的预压区面积相对误差较小，在允许误差范围内。

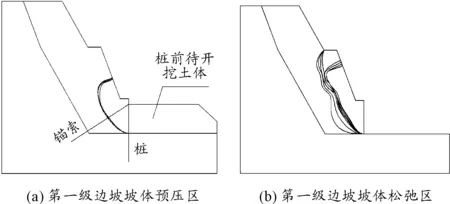
图9 第一级边坡坡体预压区

预应力F3/kN1002003004005008001000预压区面积A4/m236.3737.4438.4738.9239.2239.6740.89

2.5 第一级边坡开挖松弛区面积与该级锚索预应力的关系

模拟第一级边坡开挖过程，边坡开挖引起的松弛区范围如图10所示。第一级边坡松弛区区面积与该级锚索预应力的关系如表9所示。将F3作为自变量，A5作为因变量，对A5-F3关系进行拟合得到经验公式如下。A5为工况6引起的坡体松弛区面积，即第一级边坡开挖松弛区的面积。

A5=154.76-15.99ln(F3)

(5)

式(5)中，R2=0.985 5。经过检验，根据经验公式所求的预压区面积相对误差较小，在允许误差范围内。

图10 第一级边坡坡体松弛区

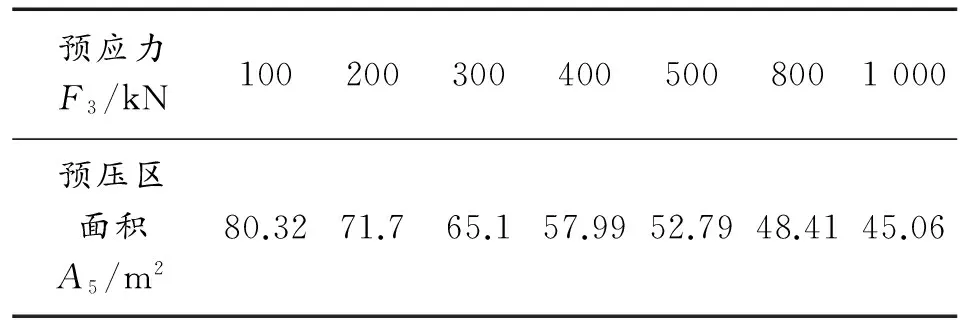
预应力F3/kN1002003004005008001000预压区面积A5/m280.3271.765.157.9952.7948.4145.06

3 结论

[1] 苏杭,周海清,李鹏举,赵帅军.基于FLAC3D的岩土边坡施工效应研究[J].后勤工程学院学报,2014(6):1-6.

[2] 周海清，刘东升，陈正汉等.某边坡工程的半坡桩方案和坡脚桩方案的比较[C]//2010全国边坡工程建设及滑坡防治技术交流会论文集.重庆:[出版单位不详]，2010.

[3] 周海清，刘东升，陈正汉等.四种基于传递系数法的滑面指标反算方法的比较研究[J].地下空间与工程学报，2010(6):1161-1167.

[4] 佘长超,陈闯,陈军,许晨.基于ANSYS的边坡开挖应力分析[J].煤炭技术,2011(7):58-60.

[5] 陈泽松,夏元友,李奇敏,张亮亮.高陡路堑边坡开挖稳定性评价及应用[J].武汉理工大学学报,2010(5):133-136,140.

[6] 孙书伟,马惠民,张忠平.顺层高边坡开挖松动区研究[J].岩土力学,2008(6):1665-1668.

[7] 王吉亮,杨静,陈又华,黄孝泉,白伟,魏雨军.复杂层状高陡岩质边坡变形与稳定性研究[J].水利学报,2015(12):1414-1422.

[8] 李明,张嘎,李焯芬,张建民.开挖对边坡变形影响的离心模型试验研究[J].岩土工程学报,2011(4):667-672.

[9] 王浩.一种确定挖方边坡开挖松弛区的数值分析方法[J].石河子大学学报(自然科学版),2011(5):623-628.

[10]肖世国,周德培.开挖边坡松弛区的确定与数值分析方法[J].西南交通大学学报,2003(3):318-322.

[11]成永刚,王玉峰.顺层挖方边坡松弛区及稳定性数值模拟分析[J].地下空间与工程学报,2013(4):848-853.

[12]袁继国,符贵军.边坡开挖松弛区划分及参数敏感度分析[J].西安理工大学学报,2013(3):301-306.

[13]冯学敏,陈胜宏,李文纲.岩石高边坡开挖卸荷松弛准则研究与工程应用[J].岩土力学,2009(S2):452-456.

[14]肖超,金福喜,刘海鸿,张可能.开挖与降雨作用下边坡失稳机理及模拟分析[J].工程地质学报,2012(1):37-43.

[15]田小波.锚喷加固边坡开挖过程锚杆轴力变化规律分析[J].交通科技,2012(5):62-64+67.

[16]肖玉辉,李振存,段劲,韦慧,曾坚.顺倾岩质高边坡开挖变形机理及计算[J].长沙理工大学学报(自然科学版),2013(2):22-27.

[17]张立舟，瞿嘉玮，邓湘波，等. 极限平衡Morgenstern-Price法与有限元ABAQUS法在边坡稳定性评价中的应用[J].重庆理工大学学报(自然科学)，2013(6)：23-27.

(责任编辑 杨继森)

Numerical Simulation on Area of Influence Zone Caused by Construction of Multistage Slope

LIANG Hua-you1a, 1b, ZHOU Hai-qing1a, 1b, ZHOU Shu-ling2, SU Hang3, LI Jian-qing1c

(1.a.Department of Civil Engineering; b.Chongqing Key Laboratory of Geomechanics & Geoenvironmental Protection; c.Department of National Defense Architecture Planning & Environmental Engineering, Logistical Engineering University, Chongqing 401331, China; 2.The 4thEngineering Design &Research Arademy General Staff of PLA, Beijing 100850, China; 3.The No.68612ndTroop of PLA, Yinchuan 750000, China)

Using FLAC3Dto complete a series of numerical simulation of the construction of multistage slope and combining CAD software to calculate the area of influence zone caused by construction, we found a function to fit the relationship between the area of influence zone and the prestress of cable. The study shows that the pre-stress of the support structure will not only cause a precompression zone with a certain area, but also reduce the area of the excavation zone of the next level slope; the relaxation zone caused by excavation and the pre-stress of anchor cable at the next level slope was imposed by a logarithmic function relation, and the precompression zone caused by pre-stress and the pre-stress of anchor cable at the same level slope was fit by the power function relationship. After inspection, the fit of the calculation formula is higher, and the correlation coefficientR2is greater than or equal 0.958, and the formula can provide certain reference basis for the designers to determine the influence zone caused by the construction of multistage slope.

numerical simulation; influence zone; pre-stress

2016-04-22；

2016-05-30

国家自然科学基金项目(41072243,41272356)；国家科技支撑计划项目(2012BAK05B02)；重庆市研究生科研创新项目(CYS16237)

梁华友(1991—)，男，硕士研究生，主要从事防灾减灾与防护工程研究。

周海清(1971—)，男，博士，教授，主要从事边坡稳定性及防灾减灾等方面研究。

10.11809/scbgxb2016.10.033

梁华友，周海清，周淑玲，等.多级边坡施工过程引起的影响区面积数值模拟研究[J].兵器装备工程学报，2016(10):152-157.

format:LIANG Hua-you, ZHOU Hai-qing, ZHOU Shu-ling,et al.Numerical Simulation on Area of Influence Zone Caused by Construction of Multistage Slope[J].Journal of Ordnance Equipment Engineering,2016(10):152-157.

TU411

A

2096-2304(2016)10-0152-06