基于蚁群算法的多连接查询优化问题研究

张兰勇，耿文杰，刘 胜

(哈尔滨工程大学 自动化学院，哈尔滨 150001)



【信息科学与控制工程】

基于蚁群算法的多连接查询优化问题研究

张兰勇，耿文杰，刘 胜

(哈尔滨工程大学 自动化学院，哈尔滨 150001)

介绍了蚁群算法在数据库查询中的应用，在给出蚁群算法的基本原理和程序流程的基础上，对传统蚁群算法进行了改进，将伪随机状态转移规则和局部信息素更新规则引入蚁群算法，提出了基于蚁群系统解决数据库多连接查询优化的方法，建立了多连接查询优化问题的数学模型，并进行了相关的实验；结果表明：当数据库的表数目较多时，基于蚁群系统算法对解决多连接查询优化问题有良好的求解性能，在求最优解品质和求最优解时间上都有较好的效果。

蚁群算法；多连接查询优化；数据库查询；最优解

多连接查询优化是数据库技术领域目前研究的一个重要方向，随着大规模数据库和数据仓库的出现，传统的查询技术已经难以满足需求，国内外的学者从不同的角度对查询优化算法进行了广泛和深入地研究。文献[1]的作者提出了基于遗传算法的分布式数据库查询优化方法，并设计了一种新的查询执行计划模型；文献[2]提出了采用改进的最小生成树算法；T.V.Vijay Kumar[3]提出一种基于遗传算法的数据库连接查询优化方法；Zehai Zhou[4]对遗传算法进行改进，但对于不同问题，需要进行相应的改进，通用性差；Po-Han Chen等[5]将模拟退火算法引入遗传算法的变异过程中，获得比遗传算法更优的数据库连接查询优化效果；Lingyun Wei等[6]利用小生境技术优点，对遗传算法探索能力进行改进，但无法改进局部探索能力差的缺陷。本文针对数据库的多连接查询优化问题，将伪随机变量和局部信息素更新规则引入蚁群算法，避免了局部最优解，提高了算法的收敛速度。

1 蚁群算法

蚁群算法(Ant Colony Algorithm，ACA)最初由意大利学者M.Dorigo提出，M.Dorigo系统阐述了蚁群算法的数学模型和机制原理，并利用该方法解决了旅行商问题(TSP)、车间作业调度问题(JSP)和二次分配问题(QAP)等一系列组合优化的问题。

1.1 基本原理

蚁群算法是模拟自然界中蚂蚁寻食的过程得出的一种模拟进化仿生算法。蚂蚁在经过的路径上会释放一种称为信息素的化学物质，从而形成信息素轨迹，在一定的范围内其他的蚂蚁会感知信息素的存在和强度。本文简要介绍蚁群搜索食物源的模拟过程。蚁群算法的原理示意图如图1。

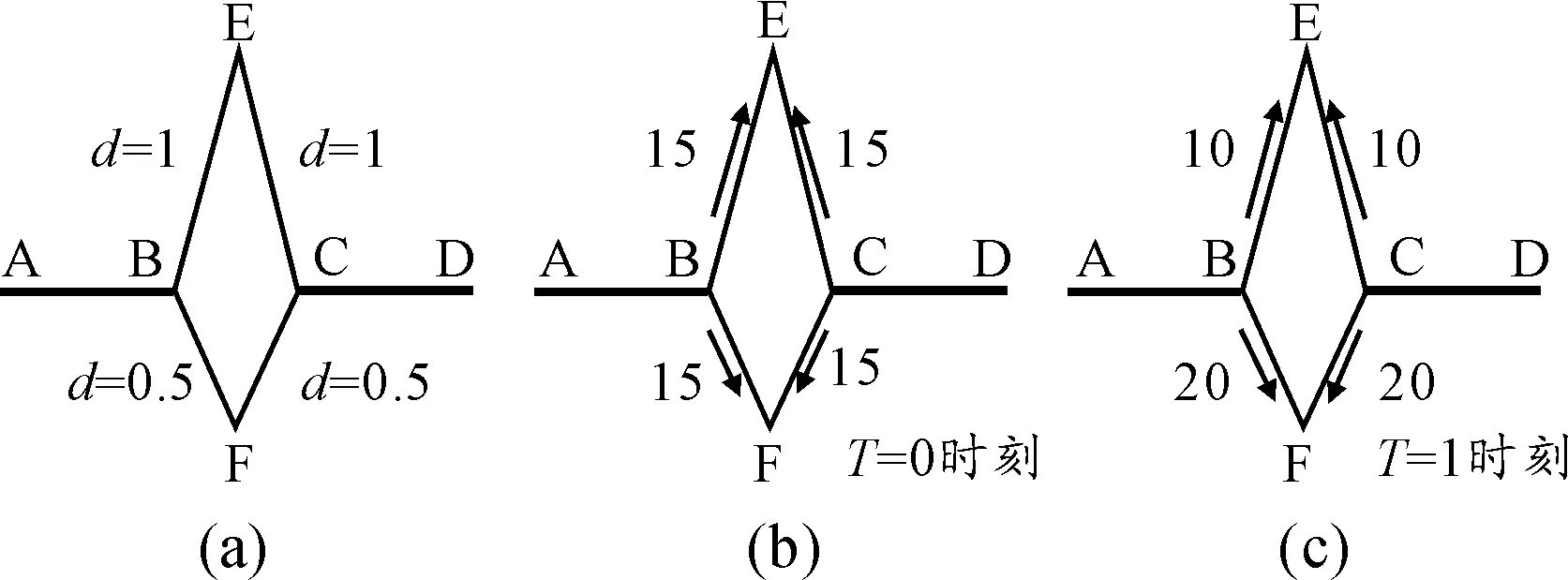
图1 蚁群算法的原理示意图

假设A是蚁穴，D是食物源，EF是一障碍物。由于障碍的存在，蚂蚁的可选择路径有：A-B-E-C-D或A-B-F-C-D。假定单位时间内从A到B的蚂蚁个数是30，从C到D的蚂蚁个数也是30，再假定信息素的停留时间是1。在初始时刻(T=0)，由于没有信息素的存在，位于B点和C点的蚂蚁可以随机的选择路径，以统计学角度分析蚂蚁选择BE、BF、CE、CF的概率是相同的，这样经过一个时间单位后，信息素在路径BFC的累积量是路径BEC上的2倍。在T=1时刻，单位时间内，将有20只蚂蚁选择BF和CF路径，而BE和CE路径只有10只蚂蚁。随着时间的累积，越来越多的蚂蚁会选择A-B-F-C-D作为蚁穴到食物源的路径，从而找到蚁穴到食物源的最短路径。张大卫等[7]提出了量子建模优化和查询的办法，为蚁群算法提出了新的方法。以下分析基本的蚁群建模算法，为深入研究做准备。

1.2 基本蚁群算法数学模型

数据库查询优化问题与传统的TSP问题(旅行商问题)非常的相似，TSP可以描述为：已知有n个城市，旅行商选择其中一个城市作为出发点，然后经过所有城市且仅经过一次，最终回到出发点，要求寻求一条距离最短的路线。对于n个城市规模的TSP问题，有(n-1)!/2条不同方式的闭合路径，TSP问题的数学模型描述表达为：

一个完全加权的向量图G=(v,A,d)，其中v={0,1,2…,n-1}是节点(城市)；集合A={(r,s)|(s,r)}∈v×v是支路集合；d是A的权函数，表示A到G上的一个映射，它将每条支路(r,s)与一个正整数权d(r,s)相关联(d(r,s)表示r和s之间的距离)，TPS问题的目标是寻找一条访问每个节点一次的最小长度的闭合回路。

描述基于蚁群算法的数学模型中符号说明如下：

n：TSP的规模；

m：蚁群中蚂蚁的总数；

τij(t)：t时刻路径(i,j)上的信息素量；

dij：元素(城市)i和元素(城市)j间的距离；

ηij：启发函数，由城市i转移城市j的期望程度；

Γ={τij(t)|cj,cj=C}：t时刻集合C中两两城市连接lij份上残留信息的集合；

在初始时刻，每一条路径上信息素量是相同的，蚁群算法在寻优过程中，蚂蚁的状态转移概率如式(1)所示：

(1)

式(2)中符号的含义：

allowedk={C-tabuk}，表示蚂蚁k下一步允许选择的节点(城市)集合；

α：信息启发因子，表示路径上积累的信息素对蚂蚁选择路径作用大小；

β：期望启发因子，表示ηij的作用，蚂蚁从城市i转移到城市j的期望程度大小，一般取ηij=1/dij，dij依据问题的实际应用确定。

蚂蚁遍历所有的城市完成一次循环后，对路径上的信息更新规则如式(2)所示：

万元工业增加值用水量 万元工业增加值用水量为工业用水量与工业增加值（万元）的比值。其中工业用水量指工矿企业在生产过程中用于制造、加工、冷却（包括火电直流冷却）、空调、净化、洗涤等方面的用水，按新水取用量计，不包括企业内部的重复利用水量。

(2)

式(2)中：ρ是信息挥发因子，用来表示随着时间的推进信息素量的衰减程度，ρ=[0,1)，(1-ρ)表示信息残留系数；τij(t+1) 是更新后的信息素量；τij(t)更新前的信息素量；Δτij是本次循环的信息素增量。

(3)

(4)

1.3 蚁群系统

蚁群系统(Ant Colony System，ACS)由M.Dorigo和Gambardella提出，用于改善蚁群的性能，ACS能在小规模的范围内一个合适的时间找到较好的解。蚁群系统的改进方面有：

1) 状态转移规则。状态转移规则提供了一个更好合理地利用新路径和先验知识的方法，表达式如下：

(5)

其中q是[0，1]之间的随机数，q0为一个状态转移参数，0≤q0≤1，V是US中某个节点，是个随机变量，根据下式的状态转移概率选取，进行下一个节点选择。

(6)

2) 全局更新规则。在最优的蚂蚁路径上使用全局更新规则来提高算法的搜索效率，其式如下：

(7)

3) 局部信息素更新规则。在蚂蚁构造路径同时使用局部信息素更新规则来提高算法的搜索效率，如下式所示：

(8)

其中，τ0为初始信息素浓度，通常取τ0=(NLnn)-1，N为节点总数，Lnn为Greedy算法求解的总距离。蚁群系统的程序流程如图2所示。

2 多连接查询优化问题

在数据库系统中执行一条查询语句涉及到多个表，在查询之前要先确定一条路径连接相关的表，在产生的多种连接可能中大部分的连接代价是不相同的，当涉及表的数量大于10个时，找到一条代价较小的路径就存在很大的困难，查询优化就是要通过一定的算法确定一条最优的表连接次序，文献[8]中提到了数据库多表查询优化的方法。以下对查询处理过程进行分析，并且建立多链接查询优化方法。

图2 蚁群系统的程序流程

2.1 查询处理

数据库的主要功能是存储和管理数据，向用户提供查询功能。Sitarz等[9]分析了模型参数的最优化评估以利于查询，当检索数据时，SQL语句向关系数据库管理系统(Relational Database Management System，RDBMS)提交请求，RDBMS处理查询过程为：RDBMS接收到查询请求(高级查询语言书写)后，首先对词法和语法进行分析，再确认语义无误后，产生查询的内部表示(一般是查询树或查询图)，然后RDBMS选择一个包含操作执行顺序、访问外部文件方式、存储中间结果的执行策略，直到最后获取查询结果。RDBMS查询执行过程如图3所示，查询优化是指在查询过程中生成的多种执行策略中，选择一个最佳执行策略的过程，文献[10]中Gao,Shangce等作者给出了大型数据的蚁群算法动态定位问题，使得查询过程更为简便迅速。

图3 查询执行过程

查询优化器的作用是产生查询执行计划((Query Execution Plan，QEP)；查询执行引擎的作用是产生执行查询的代码，并交给数据库处理器获取查询结果。

SQL语言是标准的关系查询语言，RDBMS能充分利用非过程性的语言(例如SQL语言)通过查询优化器对正在执行的查询生成一个有效的QEP，高效处理用户的查询请求。

2.2 查询优化器

用户向数据库提出查询请求Q，查询优化器的目标是选择最有效的QEP来完成对数据的读取和返回。假设S是满足Q的所有策略的集合，s是S中的元素，并且有一个相关联的代价C(s)，查询优化算法的目标是找到s0∈minC(s),s∈S。

查询优化的最终目的就是减少查询请求的反应时间，提升查询效率,Dadaneh等[11]分析了蚁群算法的可能性选择原则，提升查询效率的同时，也优化了系统的能量分配。在搜索空间较大时，如果寻找最佳QEP的优化时间过久，那优化时间和最佳QEP执行时间之和会非常大，这不符合查询优化的最终目标。

查询优化的最终目标并不仅仅是找到一个最佳的QEP，而是找到一个恰当的QEP，满足“优化时间+恰当的QEP执行时间”时间最短的条件。基于此目的，Li,B.H等[12]给出了二位平面的最优化蚁群算法，可以方便迅速定位。

一个查询多数情况下对应多个QEP，这是由于一个查询请求对应着大量的等价关系的代数表达式，并且任何一个代数表达式都可由大量的QEP实现。Mi,Nan等[13]进行了限制区域的蚁群最优分配方法，用于锁定求解空间。随着Q中关系数的增加，Q对应的代数表达式集合和Q对应的QEP集合会以指数幅度增长。查询优化器对高级查询语句的转换过程示意图如图4所示。

图4 高级查询语句的转换过程示意图

查询优化器在浩瀚的搜索空间中，按照一定的原理依据代价估计函数评估所有的QEP，估计对应的代价，从中选取代价最小的QEP。

2.3 多连接查询

多连接查询((Multi-Join Query，MJQ)是指仅包含Select、Project、Join的查询(SPJ查询)经过投影、选择操作并在优化后得到的N个基关系连接操作构成的关系代数表达式。

对于多连接查询得到一个优化的关系连接次序是查询优化的核心，Xu,Bo等[14]给出了查询过程中的最小限制下的最优评估，查询优化器在对一个多连接的查询优化过程会使用不同方式的查询表示，以下对查询图、连接树和操作树3种多连接查询表示形式进行说明。查询图形式在查询执行过程的初期经过语法、词法分析和语义确认后采用，中间经查询优化器转换成的关系代数表达式采用连接树形式。操作树形式在最后物理优化后的最佳QEP采用。

2.3.1 查询图

在多连接查询中，join查询图为G=(V，E)，R∈V表示待连接关系，用大写字母表示；(R1,R2)∈E表示一个连接操作，用数字表示。对于一个多连接查询：(AjoinB)and (BjoinC)and (CjoinD)and (CjoinE)的查询图如图5所示。

2.3.2 连接树

查询图的每个可能的查询计划可由连接树表示，叶子的节点表示数据库的连接关系，中间节点对应左右节点连接的结果集，操作的顺序是从上到下。图6描述了图5中查询图三种不同的查询执行计划。

图6 连接树

逻辑优化的目的是确定一个合适的join树，左深树是最常用的连接树，本文采用以往查询优化算法中通用的策略，采用左深树作为搜索策略空间。

2.3.3 操作树

操作树通常用来表示查询请求经过物理优化后，得到的实际连接的物理操作执行顺序。图7表示图6连接树中左深树物理优化后的一个操作树。连接操作实现的算法一般有嵌套循环连接(Nested Loop Join)、合并连接(Merge Join)、哈希连接(Hash Join)、索引连接(Index Join)。

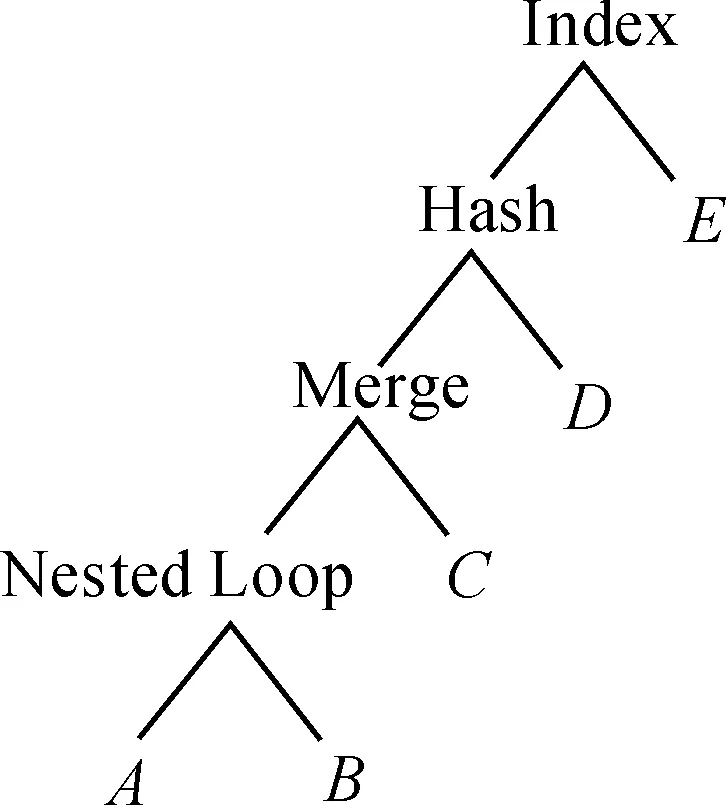
图7 操作树

2.4 多连接查询优化

多连接查询优化(Multi-join Query Optimization，MJQO)是指在搜索的策略空间中找到一个最优的join树，并且为join树中的每个连接操作选取有效的join方法，MJQO问题也是逻辑优化和物理优化问题。Talafuse,T.P等[15]建立了冗余分配计算方法，可以借鉴到多链接优化查询中。多连接查询优化算法的执行时间长短和寻找到的QEP的大小代价取决于以下3个方面：

2.4.1 搜索空间

一个多连接查询包含大量的QEP，这构成了该多连接查询的策略空间，一般而言策略空间很大，查询优化算法通常不在整个策略空间搜索，而是在最佳的QEP可能存在的空间搜索，这个策略空间的子集就是搜索空间。

搜索策略空间一般分为3种，分别是最佳QEP、有效QEP和低效QEP。

2.4.2 代价估计函数

查询执行计划的代价包括：I/O代价、存储代价、计算代价和通信代价，分别以字母I、S、E、C表示，代价的权值分别用Pi、Ps、Pe、Pc表示，则查询执行计划的表达式如下式，其中Pi+Ps+Pe+Pc=1。

Cost=I*P+S*P+E*Pe+C*Pc

(9)

假设一个含有n个关系的连接树，(j1,j2,…,ji)是连接树的非叶子节点(内部节点)，则代价评估模型如下式：

(10)

对于一个连接JjoinS代价的计算式如下式。

(11)

其中V(c,R)的计算式如下式所示

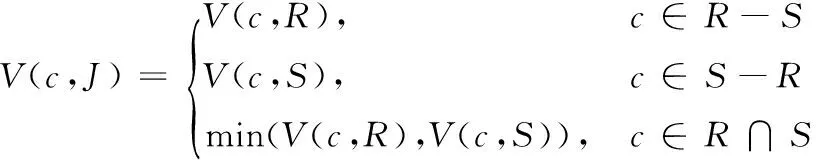
(12)

2.4.3 搜索算法

查询优化器的搜索算法目标是在一个指定的搜索空间找到一个高效的QEP。

确定搜索空间后要选定一种高效的搜索算法，满足“优化时间+恰当的QEP执行时间”时间最短。查询优化搜索算法大致分为穷尽搜索算法、局部随机搜索算法和启发式搜索算法3种。蚁群算法属于启发式搜索算法，本文针对改进的蚁群算法对查询优化器的搜索算法进行分析研究。

3 蚁群算法对多连接查询优化问题的描述

通过对多连接查询优化问题的描述，对比典型的TSP问题，可以发现多连接查询优化问题和TSP问题有很多的相似之处，将数据库中的每个关系(表)当作一个城市，将两个关系(表)之间的join方法(连接代价)当作一个城市到另一个城市的开销，这样多连接查询优化问题就转换为类似TSP的问题，而蚁群算法能够很好地解决TSP问题。

本文采用左线性树空间作为搜索空间，多连接查询优化问题可以简单地描述为：以顶点集V中所有的顶点作为叶节点构造一棵最小代价的二叉树(QEP)，每个顶点出现并仅出现一次。

MJQO问题和TSP问题也存在着明显的差别，为了简化问题，本文只考虑的区别是MJQO问题的任意一个解中，vi和vj两个相邻的顶点之间的代价不固定，由顶点vi、vj本身和vi、vj之前的顶点集合的共同特点决定。

基于左线性空间多连接查询优化问题(L-MJQO)，考虑到查询执行计划在时间和空间上的复杂性，并且其价评估取决于操作结果集的记录数目，所以将L-MJQO问题简化为查询中n个表(关系)的join树连接次序的逻辑优化问题，这样多连接查询优化问题就转化成类似典型TSP问题。

采用避免笛卡尔积当作启发信息来缩小搜索空间，图8给出了基于蚁群系统的L-MJQO算法流程图。

算法的主要步骤如下：

步骤1：初始化参数(信息素分布参数等)；

步骤2：将m只蚂蚁随机地置于查询图的某一顶点；

步骤3：设置蚂蚁的状态向量Tag=[0…0]，Tag(k)=0表示第k只蚂蚁要继续添加接成分；Tag(k)=1表示第k只蚂蚁已经完成了解构造；

步骤4：判断是否所有的蚂蚁均完成解构造，即判断是否Tag=[1…1]，若满足条件则执行步骤9，否则令k=1；

步骤5：判断第k只蚂蚁是否完成解构造，若满足则执行步骤8，否则按照状态转移规则选择先一个与当前结果不产生笛卡尔积关系的关系节点；

步骤6：使用局部信息更新规则对刚走过的路径修改信息素量；

步骤7：依据搜索停止函数判断该蚂蚁是否满足解构造，满足则Tag(k)=1；

步骤8：判断是否k=m，满足则执行步骤10，不满足则令k=k+1执行步骤5；

步骤9：依据适应度评价函数计算蚂蚁所构造的m个QEP的适应值，并记录当前最优解；

步骤10：使用全局信息素更新规则对全局最优解所处的路径修改信息素量；

步骤11：判断是否满足停止条件，满足则算法停止，否则执行步骤2。

该算法的输入量是查询Q涉及的所有的基关系的集合，输出量是查询Q中查询代价最小的QEP。

下面结合多连接查询优化问题对个别参数进行。

Nc：迭代次数；

table：一个多连接查询包含的表信息(表的编号和基数)；

attribute：表之间的公共属性信息矩阵(表的编号、公共属性编号和该公共属性在表中取不同值的个数)；

graph：表之间表示查询图的连通关系矩阵；

ηij：定义ηij=D(j)/N(j)为启发式信息；

τ0：信息素初始值τ0=1/NCmin，N是查询Q涉及的基关系总数，Cmin是查询Q采用Greedy算法得到的最小QEP的代价。

局部搜索算法：采用Greedy算法(图8)。

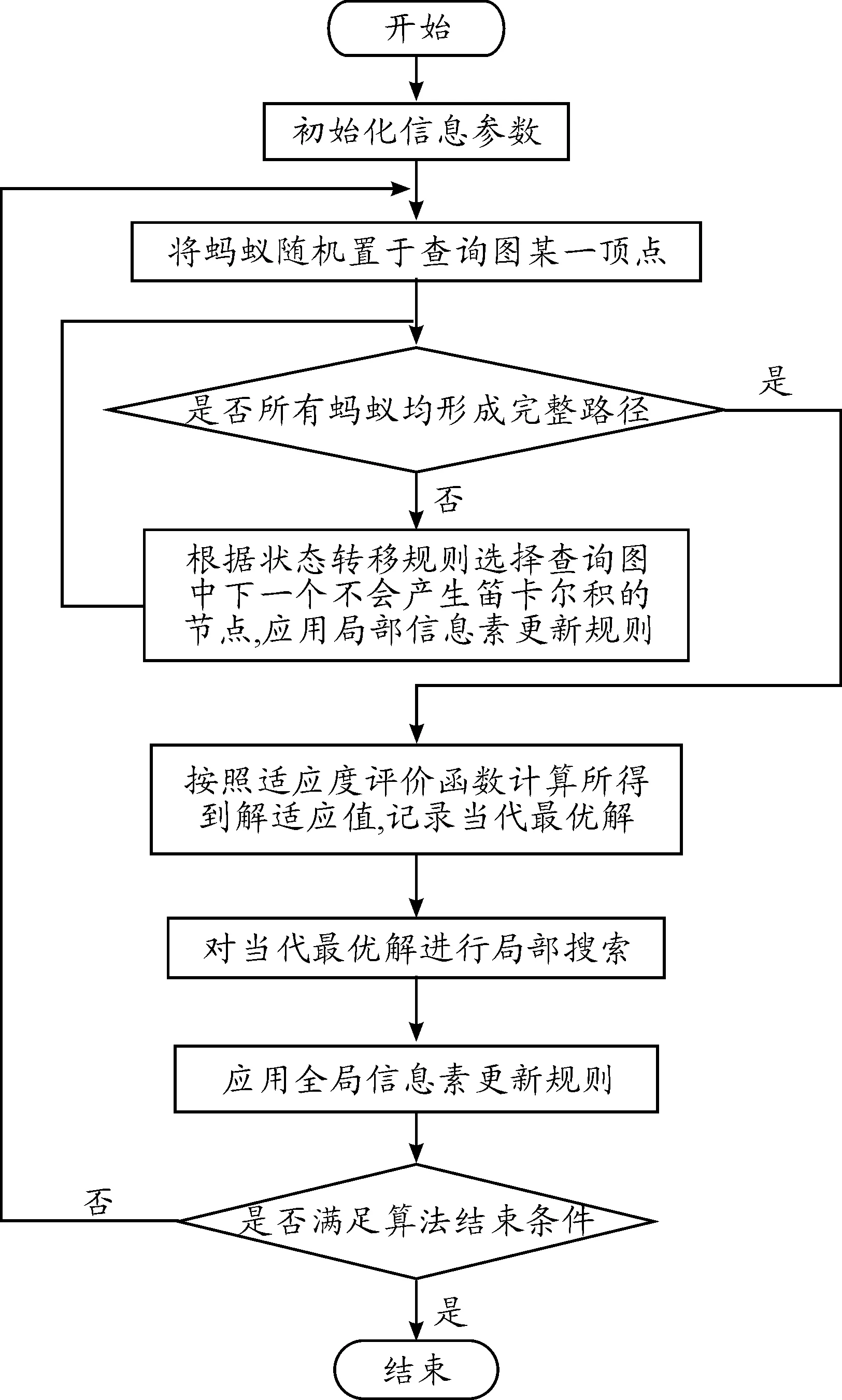
图8 基于蚁群系统的L-MJQO程序流程

4 实验结果及分析

4.1 算法参数设置的影响

蚁群算法中参数的选择对其算法性能有重要影响，但其选取的方法和原则一般是依据实验经验确定。本节的实验主要研究α、β、ρ三个参数的不同取值对算法的影响，讨论其设定的最佳原则。

实验数据为5个关系表n=5，迭代次数为N=200，蚂蚁的数目选取经验值m=10，q0=0.2，取α=1，β=4，ρ=0.5，实验内容仅考虑α、β、ρ值对算法的影响，所以其他参数的值保持不变，依次改变α、β、ρ的值，运行次数为50，取最优解的平均值，得到仿真结果。

1) 信息挥发因子对算法的影响，取α=1，β=4，ρ的取值为0，0.1，0.2，…，1，ρ的每个数据各自运行50次，取最优解的平均值，得到信息挥发因子对算法的影响如图9所示。

当ρ∈[0.5,0.8]时，最优解比较稳定，算法的性能比较好。这是因为ρ的双重性，当ρ较小时，路径上的残留信息较多，正反馈作用减弱，蚂蚁搜索的随机性增强，算法的收敛速度慢；当ρ较大时，正反馈作用增强，蚂蚁搜索随机性减弱，算法的收敛速度加快，但容易陷入局部最优。

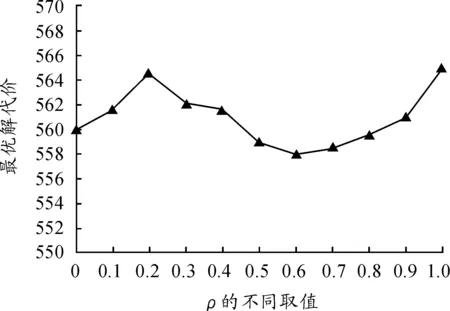
图9 信息挥发因子对算法的影响

2) 信息启发因子对算法的影响，取β=4，ρ=0.5，α的取值为0，0.5，1，…，5，α的每个数据各自运行50次，取最优解的平均值，得到信息启发因子对算法的影响如图10所示。

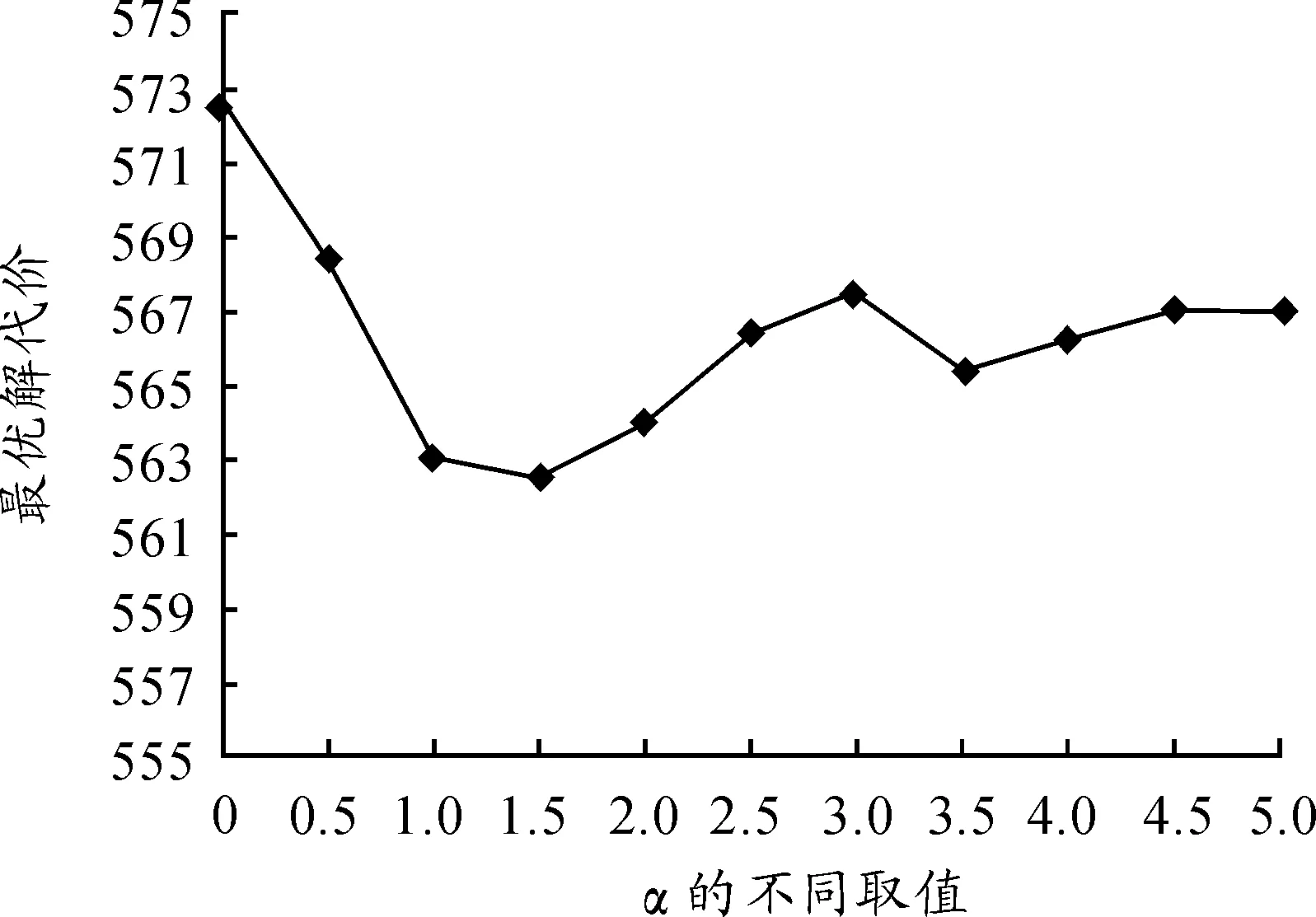
图10 信息启发因子对算法的影响

当α∈[1,2]时算法有较好的求解性，这是由于在α较大时，对蚂蚁运动的指导性程度强，走过重复路径的可能性小，搜索随机性减弱；α较小时，蚂蚁的搜索会过早的陷入局部的最优解。

3) 期望启发因子对算法的影响，取α=1，ρ=0.5，β的取值为0，1，2，…，10，α的每个数据各自运行50次，取最优解的平均值，得到期望启发因子对算法的影响如图11所示。

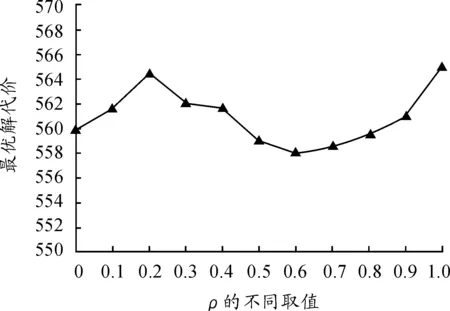
图11 期望启发因子对算法的影响

当β∈[2,5]时算法有较好的求解性，这是因为β表示蚂蚁在运动过程中启发信息对蚂蚁搜索指导的重要程度，在β过大时，启发信息的作用程度增加，减弱了蚂蚁搜索的随机性，蚂蚁的搜索易限于局部的最优解。

由以上的实验数据可知，α、β、ρ参数的取值对算法的影响很大，所以在采用蚁群算法解决多连接查询优化问题时，要合理的设置α、β、ρ值。

4.2 算法求解性能比较

本节在讨论相同的实验条件下，针对多连接查询中表个数的不同，比较Greedy算法、遗传算法和蚁群算法3种不同算法求解时的查询执行代价和QEP的生成时间，每个算法运行40次，然后取平均值。

遗传算法参数：N=50，Pc=0.6，Pm=0.12，进化代数G=100。

蚁群算法参数：α=1，β=3，ρ=0.8，q0=0.2蚂蚁个数m=10，迭代次数N=200。

1) 取多连接查询的关系表的个数为5，10，15，…，50，计算遗传算法和Greedy算法的查询执行代价，并除以蚁群算法得到的查询执行代价，得到一个标量值。其结果如图12所示。

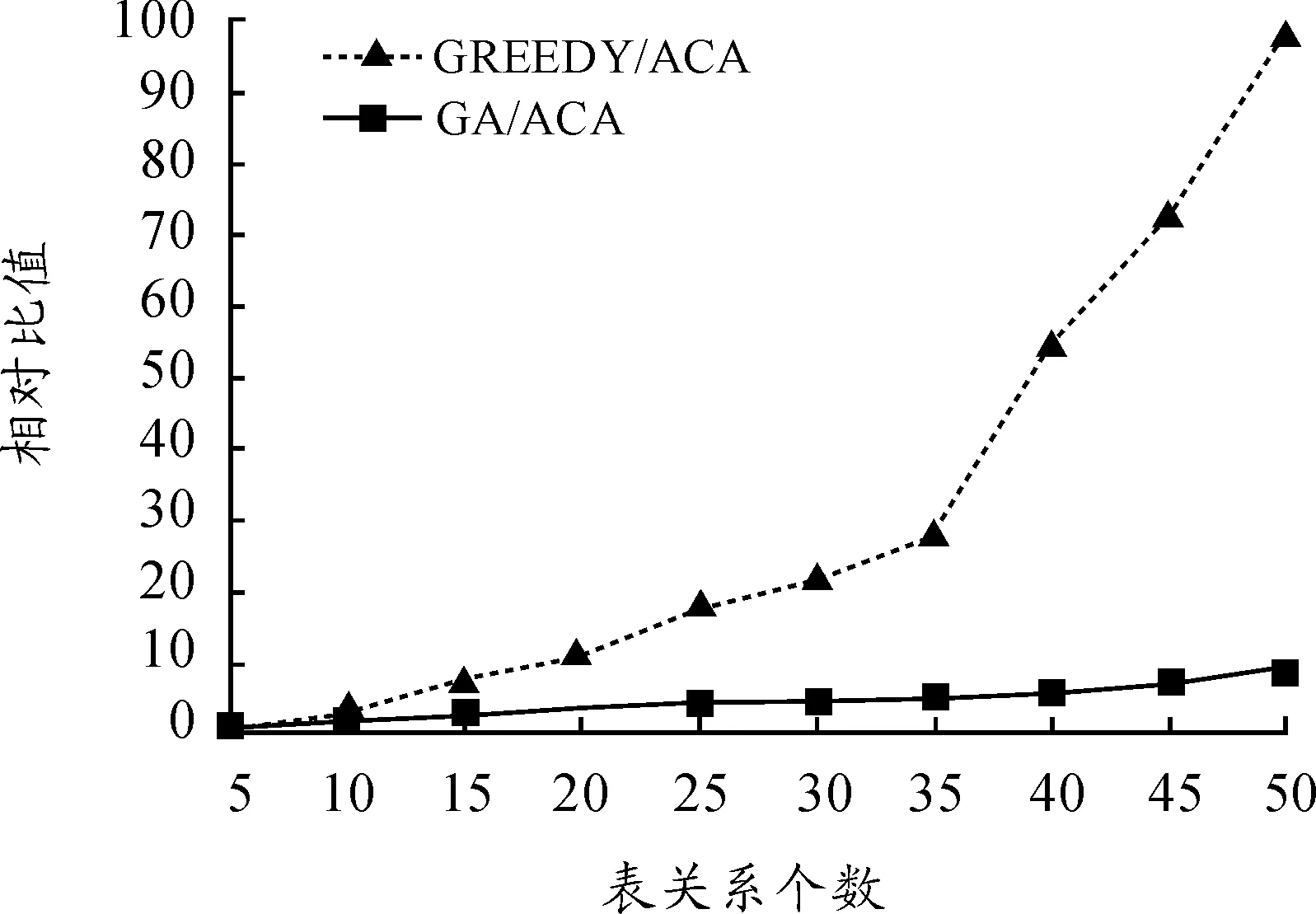
图12 查询代价比较

遗传算法和Greedy算法求得的最佳QEP的代价均大于蚁群算法，并且随着表个数的增加，其执行代价比值也逐渐增加，Greedy算法的执行代价增长幅度比遗传算法高很多。当表的数目是50时，遗传算法执行代价是蚁群算法的10倍左右，Greedy算法执行代价是蚁群算法的100倍左右，所以当表的数目较多时，遗传算法和Greedy算法不适合用于多连接查询的优化。

2) 取多连接查询的关系表的个数为5,10,15，…,50，分别得到蚁群算法、遗传算法和Greedy算法的最优QEP的运行时间，其结果如图13所示。

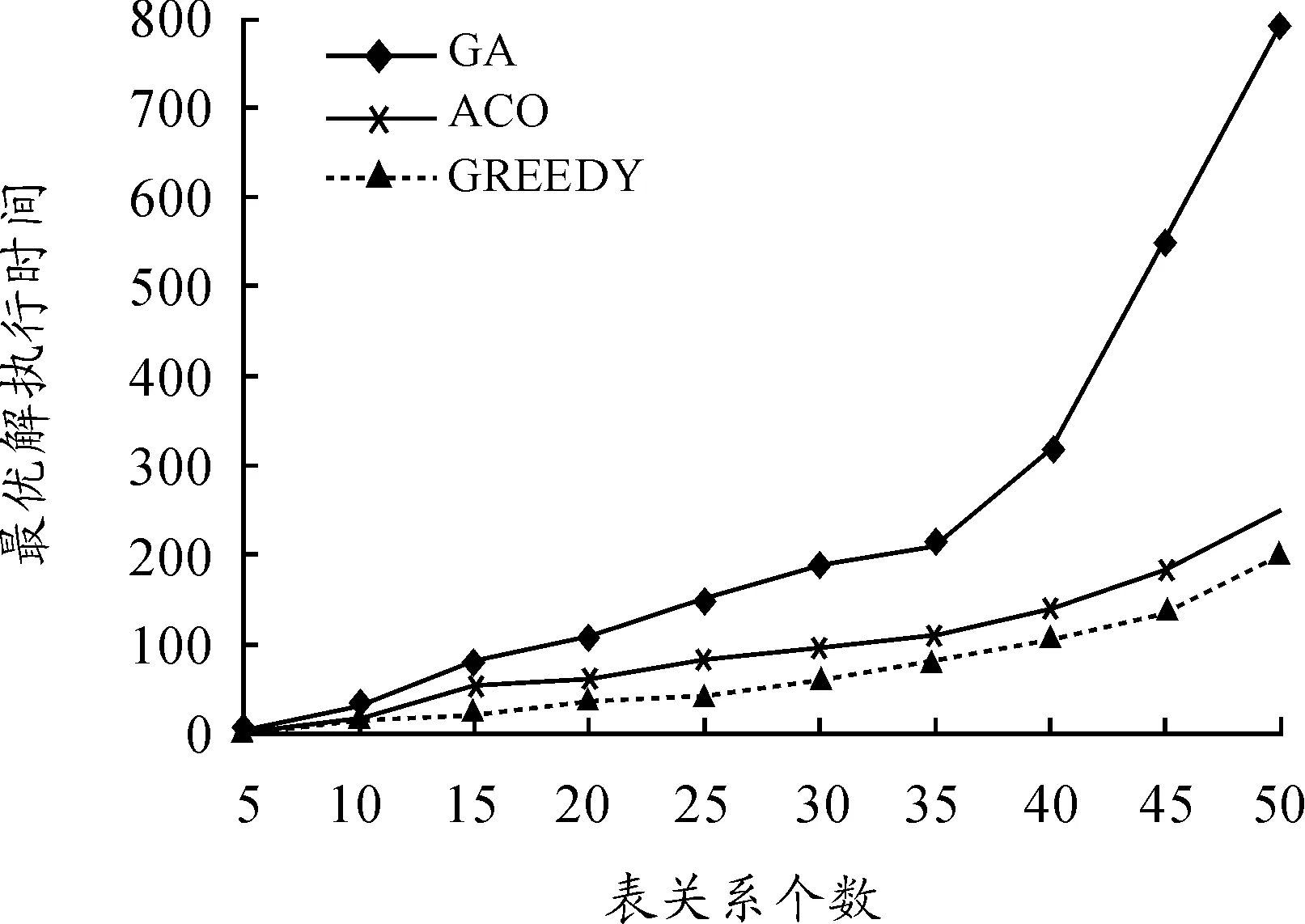
图13 最优解时间比较

随着表的个数增加3种算法求得最优解的时间都有所增加，其中遗传算法的增长速度最快，Greedy算法和蚁群算法的增长比较平缓，由于Greedy算法没有迭代计算的过程，所以求解的时间最短。

随着表数目由5～50变化时，上述3种算法的查询代价和最优解时间如表1和表2所示。

综合比较可以得出，Greedy算法求解过程时间较短，但运行的查询执行代价过大，求解品质变差，求解结果变得不再可用；遗传算法运行过程的执行代价较小，但最优解的执行时间过长，查询效率较低。所以，当表数目较大时，蚁群算法在求解品质和求解时间都比较好。

表1 查询代价

表2 最优解时间

5 结论

多连接查询优化是个复杂的问题，本文采用基于蚁群系统实现多连接次序的优化，引入局部信息素更新规则和伪随机变量，找出最优的连接路径。通过实验结果表明，在大型的数据库查询中，可以利用蚁群算法提高求解性能和求解速度，这对数据库查询设计和实践有重要的借鉴作用。

[1] 崔峰峰,南振岐.基于蚁群算法的分布式数据库查询优化方法[J].计算机时代,2014(5):47-49.

[2] 胡枫.一种分布式数据库多元连接查询优化算法及改进[J].计算机工程与应用，2011(16):125-127.

[3] VIJAY KUMAR T V.Vikram Singh and Ajay Kumar Verma.Distributed Query Processing Plans Generation Using Genetic Algorithm[J].International Journal of Computer Theory and Engineering,2012,3(1):38-45.

[4] ZHOU ZEHAI.Using Heuristics and Genetic Algorithms for Large-scale Database Query Optimization[J].Journal of Information and Computing Science,2010,2(4):261-280.

[5] CHEN POHAN,Seyed Mohsen Shahandashti.Hybrid of Genetic Algorithm and Simulated Annealing for Multiple Project Scheduling with Multiple Resource Constraints[J].Automation in Construction.2012,18(4):434-443.

[6] WEI L Y,ZHAO M.A Niche Hybrid Genetic Algorithm for Global Optimization of Continuous Multimodal Functions[J].Applied Mathematics and Computation,2013,160(3):649-661.

[7] 张大卫,李涛.基于量子蚁群算法的数据库连接查询优化[J].微型电脑应用,2014(5):40-43.

[8] 李文俊,张爱林.数据库多表查询优化技术[J].计算机系统应用,2014(6):54-59.

[9] SITARZ,PIOTR,POWALKA,BARTOSZ.Modal Parameters Estimation Usingant Colony Optimization Algorithmn[J].Mechanical Sysems and Signal Processing,2016(76/77):531-554.

[10]GAO,SHANGCE,WANG,YIRUI,CHENG,JIUJUN.Ant Colony Optimization with Clustering for Solving the Dynamic Location Routing Problem[J].Applied Mathemamatics and Computation,2016(285):149-173.

[11]DADANEH,BEHROUZ ZAMANI,MARKID,HOSSEIN YEGANEH,ZAKEROLHOSSEINI.Ali Unsupervised Probabilistic Feature Selection Using ant Colony Optimization[J].Expert Systens with Application,2016(53):27-42.

[12]LI B H,LU M,SHAN Y G. Parallel Ant Colony Optimization for the Determination of a Point Heat Source Position in a 2-D Domain[J].Applied Thermal Engineering,2015(91):994-1002.

[13]MI,NAN,HOU,JINGWEI,MI.Wenbao Optimal Spatial Land-use Allocation for Limited Development Ecological Zones Based on the Geographic Information System and a Genetic Ant Colony Algorithm[J].International Journal of Geographical Information Science,2015,29(12):2174-2193.

[14]XU BO,MIN.Huaqing Solving Minimum Constraint Removal (MCR) Problem Using a Social-force-model-based Ant Colonyalgorithm[J].Applied Soft Computing,2016,(43):553-560.

[15]TALAFUSE T P,POHL E A.A Bat Algorithm for the Redundancy Allocation Problem[J].Engineering Optimizaton 2016,48(5):900-910.

[16]张正柱，刘林真．基于WebService的烟花溯源查询系统的设计与实现[J].重庆理工大学学报(自然科学)，2015(2)：82-85.

(责任编辑 杨继森)

Research on Multi-Join Query Optimization Based on Ant Colony Algorithm

ZHANG Lan-yong, GENG Wen-jie, LIU Sheng

(College of Automation, Harbin Engineering University, Harbin 150001, China)

This paper introduced the ant colony algorithm (ACA) to the database query. It listed the basic principles and program process and improved the traditional ACA. The local pheromone update rule and pseudo-random proportion were introduced to the ACA, and then this paper built a multi-join query optimization model based on ant colony system (ACS), and experiments were carried out. The experiments show that this algorithm has the better effect on optimal solution quality and optimal solution time of multi-join query optimization problem when the number of tables is large in your database.

ant colony algorithm; multi-join query optimization; database query; optimal solution

2016-05-10；

2016-06-15

国家自然科学基金(51579047); 国家科技支撑计划(2013BAG25B01)；毫米波国家重点实验室开放课题(K201707);MPRD专项资助(IEP14001)；博士点基金(20132304120015)；中央高校基本科研业务费(HEUCF160414)

张兰勇(1983—)，男，博士，讲师，主要从事控制理论与控制工程、随机信号处理等研究。

10.11809/scbgxb2016.10.015

张兰勇，耿文杰，刘胜.基于蚁群算法的多连接查询优化问题研究[J].兵器装备工程学报，2016(10):72-79.

format:ZHANG Lan-yong, GENG Wen-jie, LIU Sheng.Research on Multi-Join Query Optimization Based on Ant Colony Algorithm[J].Journal of Ordnance Equipment Engineering,2016(10):72-79.

TP311

A

2096-2304(2016)10-0072-08