基于改进蚁群算法的交通最优路径方法研究
2016-11-17张继荣袁晓洁
张继荣,袁晓洁
(西安邮电大学 通信与信息工程学院,西安 710061)
基于改进蚁群算法的交通最优路径方法研究
张继荣,袁晓洁
(西安邮电大学 通信与信息工程学院,西安 710061)
针对日益复杂的交通网络,提出了一种基于改进蚁群算法的交通路径最优方法,首先根据图论的思想构建了城市交通网络模型,结合层次分析法考虑了道路长度、交叉口停滞、交通拥挤、道路容量、天气状况等5个主要因素;然后在MATLAB平台下,采用改进的蚁群算法对静态交通网络和动态交通网络分别进行最短路径的求解,最后进行了对比分析;研究结果表明,在综合考虑以上5种因素的情况下,动态交通网络下的路径最优算法能为出行者找到更准确更便捷的路线。
蚁群算法;动态交通;路径最优
0 引言
随着社会的发展、生活节奏的加快,小轿车的使用越来越普遍。这固然提高了人们的出行效率,但由此也引发了诸如交通拥堵、环境污染等一系列问题。作为一名驾驶员,希望选择一条距离最短,用时最少的道路。但一条路径的好坏不仅取决于道路长短,还取决于道路容量、天气状况、交通堵塞等动态因素。因此,如何在复杂的交通网络中找出一条实时、有效的路径,是当下人们极为关注的问题。
国内外关于最短路径选择算法的研究成果有很多,目前常用的算法主要有:Dijkstra算法、Bellman-Ford算法和蚁群算法等[1]。蚁群算法是一种经典的路径优化算法,由于具有较强的鲁棒性和发现较好解的能力[2],已经先后应用于调度问题、旅行商问题。Gambardella等[3]提出了双蚁群系统求解车辆路径问题,两个蚁群依靠独立的信息素分别优化两个目标函数,并通过共享最优路径来交换信息。RongweiGan[4]和QingshunGuo[4]提出用改进的蚁群算法来解决旅行商问题,将蚂蚁分成两组,并通过优化搜索方式来达到路径寻优的目的。
但是,很多学者主要利用蚁群算法对如何寻得最优路径进行了理论研究,却很少有学者用它解决现实生活中的交通路径选择问题[5]。本文针对蚁群算法搜索效率低下、易陷入局部最优解[6]等缺陷,采用改进的蚁群算法,致力于找出一种最短路径寻优方法,在考虑诸多动态因素的情况下,使出行者找到一条快速到达目的地的最优路径,不仅节约时间、降低交通压力,而且减少污染。
1 构建交通网络模型
在实际情况下,交通网络错综复杂,要将交通路网抽象成图的形式以便进行研究,这个抽象的过程十分重要。
下面从西安市的地图上截取一段平面图,将交叉路口抽象为节点,将节点之间的路段抽象成边,并对每个节点进行编号,节点之间的距离取实际距离。则整个路网模型用赋值的有向图T=(G,F,W,R)来描述,其中:G={ni|i=1,2,…,n}是节点集合,如图1中节点1到节点19;F={f

图1 交通网络模型
建立交通网络模型以后,其最优路径求解问题就等价于从图T=(G,R,W,F)中搜索两个特定节点之间的权值最小路径问题。
2 蚁群算法及改进
2.1 传统的蚁群算法
蚁群算法[2]是一种基于种群的启发式仿生进化算法,最初是用来解决TSP(Traveling Salesman Problem)问题的。其过程可以描述如下:首先,将m只蚂蚁随机的放到n个网络模型节点上,并使用禁忌表(tabuk)来记录蚂蚁k访问过的节点。设置每只蚂蚁禁忌表的第一个元素为当前所在节点,此时,各路径上的信息素量相等;其次,每只蚂蚁独立选择下一节点,且蚂蚁k从节点i转移到节点j的概率[2]为:
(1)
式中,Jk(i)={1,2,…,n}-tabuk是蚂蚁k下一步可选节点的集合;ηij(t)是启发式因子,表示从节点i到节点j的期望强度,值为两节点之间距离的倒数;α,β是权衡因子,决定了信息素和启发式信息的相对影响力。
最后,当节点上的所有蚂蚁都完成一次周游后,各路径上的信息素会按以下两式[7]进行实时更新:
(2)
(3)

(4)
式中,Lk表示第k只蚂蚁遍历所有节点所走的长度,Q表示一个正常数。
2.2 算法存在的问题及改进
蚁群算法在寻找最优路径方面的优势毋庸置疑,但传统的蚁群算法同时也存在一些缺陷,具体主要表现在两个方面:
1)蚁群算法在最优路径搜索过程中缺少方向性的引导信息,这会直接降低搜索效率。
2)容易陷入局部最优解。由于算法存在信息素的正反馈作用,导致经过若干次的搜索循环以后,局部最优解产生的信息素浓度增加,造成所有的蚂蚁个体都趋向于这一个局部最优解,从而陷入局部最优。
针对以上两个缺陷,本文做出了相应的改进。
1)启发式因子ηij(t)的改进。
(5)
式中,wij表示弧
2)给信息素设定门限。
在算法初始时刻,给每条路径上的信息素都先设定两个门限值τmax(较大常数),τmin(较小常数)。这样,信息素更新对路径信息素含量的影响降到了最低,蚂蚁也有了更大的搜索空间。为保证向最优方向收敛,每进行一次循环,都只对得出最优解的蚂蚁走过的路径进行更新,其他路径不更新。则信息素的值可以表示为:
(6)
2.3 改进算法步骤
1)参数初始化。设定N=0(N为蚂蚁迭代次数),信息素τij=0,将m只蚂蚁随机摆放到初始点上[8]。
2)设置禁忌表。令禁忌表的第一个元素为k= 1,蚂蚁数量的变化为k=k+1。
3)实现蚂蚁移动。按公式(1)、(5)计算转移概率,概率值决定了蚂蚁移动的方向。
4)修改禁忌表。当蚂蚁从节点i到达节点j时,更新其信息素并修改禁忌表,同时将新节点j置于禁忌表tabuk中。
5)重复执行以上4个步骤。直到每只蚂蚁都遍历完集合中的所有节点,终止循环。
6)对蚂蚁找到的每一条最优路径,按公式(2)、(3)、(4)、(6)进行信息素更新。
7)确定最优路径。从众多新生成的可行解中找到一条最短路径,即为本次迭代的最优路径。
8)重复执行以上步骤。若直到连续多次循环迭代没有出现更优解,则停止运算,输出当前值作为最优解;否则清空禁忌表,跳转到第2)步执行。
3 道路网各因素的权值
3.1 层次分析法
层次分析法(Analytic Hierarchy Process, AHP),是计算道路权重的关键方法。它将定性和定量相结合[9],根据各个因素相互联系的有序层次,对每层的各因素进行直观判断,然后做出相对定量的表示,最后建立数学模型。
3.2 路况影响因素
使用层次分析法之前,需要列出影响交通路况的各个因素,本文主要考虑五种因子:
(1)路径长度。即静态距离,其值为实际长度,交通路网模型已经给出。
(2)交叉口停滞。交叉口设立了红绿灯,斑马线人流通行密集,部分车辆还会转向,很容易发生交通事故。因此,交叉口是最容易发生时间延误的地方。
(3)交通拥挤度。它反映交通的繁忙程度,与速度、行车密度、交通量等紧密相关。
(4)道路容量。道路容量是指单位时间内可以通行的最大车流量,它与道路等级息息相关。
(5)天气状况。这是一个很随机的因素,晴空万里时,人们都能够正常出行。但偶尔也会遇到浓雾、暴雨、大雪等天气,一旦出现就直接影响行车安全以及出行效率。
3.3 判断矩阵和各因素的路径权值
由于各因素的权重不仅仅只是定性的表示,还要有定量的结合。所以,Saaty等人提出了一致矩阵法,即不把所有因素都放在一起比较,而是两两进行比较[10]。这种方法,以计算相对尺度的形式,减少了性质不同的诸因素之间相互比较的困难,使准确度大大提高。
判断矩阵表示本层中所有因素(指5种路况因素)与目标层(指路径选择)的相对重要性的比较。判断矩阵的元素αij用Saaty的1-9标度方法给出,本文只考虑5个因素,其中A1、A2、A3、A4、A5分别代表路径长度、交叉口停滞、交通拥挤度、道路容量、天气状况。判断矩阵的标度及含义如表1所示。
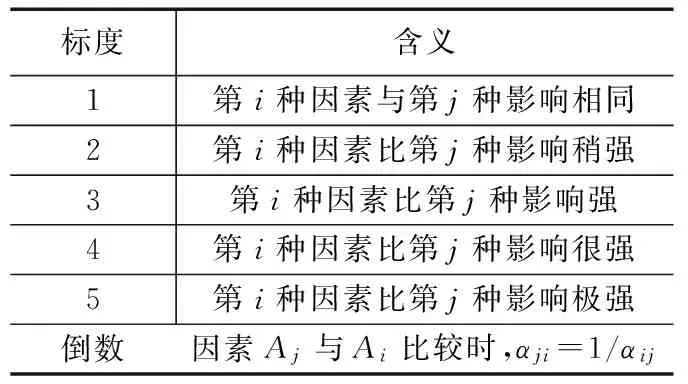
表1 判断矩阵的标度及含义
依据交通规划中各评价指标的重要程度[11],经过现场调研,并通过咨询专家意见,在全面了解西安市交通运输质量评价指标的基础上,得出的判断矩阵如表2所示。

表2 判断矩阵
于是,可以得到判断矩阵Aij:
经过归一化计算,得到权向量为:w=(0.150 6,0.252 2,0.422 4,0.0102,0.072 8)T)。同时,求得矩阵的最大特征根为λmax=5.02,也即λmax>n(n为判断矩阵阶数),满足一致性检验要求。
3.4 路径权重的确定
基于以上计算,已经知道5种路况因子的权向量,就可以计算整个网络中各条路径的权重值W,方法如下[12]:
(7)
式中,w1~w5是各动态因子的权值向量,由判断矩阵已经得出结果;s是路径距离,v是道路平均时速,s/v是路径参量,可以根据路网模型设定;m是交叉口停滞参量,根据延误时间由短到长,可划分为[0.2,0.4,0.6,0.8,1.0]几个等级;n是交通拥挤程度的权值参数,按照拥挤程度不同,交通状态和权值系数可分别表示为非常畅通状态(0≤M<0.2)、标准畅通状态(0.2≤M<0.4)、轻微拥堵状态(0.4≤M<0.6)、拥堵状态(0.6≤M<0.8)、严重拥堵状态(0.8≤M<1.0)等五种情况[13];p是道路容量的参数,根据道路等级,要在[0,1]区间内赋值;q是天气状况参量,可用0表示天气晴朗,0.2表示小雨,0.4表示大雨,0.6表示雾天,0.8表示雪天。
3.5 静态和动态路径距离求解
取交通网络抽象图的前10个节点,并设置节点1为起点,节点10为终点。设定天气状况为晴朗,即权值系数为0。则各个动态因子的取值情况以及根据各个因子求出的静态距离(sd)、动态距离(dd)如表3所示:

表3 静态和动态距离求解情况
4 算法仿真
根据前面表格里得到的每条道路的权重值,基于改进的蚁群算法,将程序在Windows7环境下通过运行MATLAB7.0进行仿真,并设置循环次数为30次。得到静态和动态条件下最优距离的仿真图分别如图2、图3所示。
由仿真结果可以得出最优解的情况,如表4所示。

表4 最优解情况

图2 静态最优距离
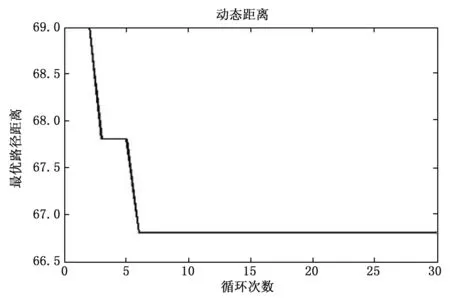
图3 动态最优距离
由表4可以看出,静态条件下选择的最优路径1-4-5-6-10,在综合考虑了几种动态因素之后,距离变成了99.2,比动态选择的最优路径1-4-8-9-10多出了32.4的距离,两者之间的差距还是很大的。
5 结束语
本文在改进的蚁群算法基础上,结合层次分析法加入了几种路况动态因子,并在MATLAB平台下对静态和动态路况分别进行了仿真。仿真结果表明,在综合考虑各种路况因子的情况下,动态规划出来的最优路径能为出行者找到更快更便捷的路线。
[1] 王一松.基于实时交通信息的最优路径规划算法的研究与实现[D].上海:东华大学,2013.
[2] 赵燕伟,张景玲,王万良.物流配送的车辆路径优化方法[M].北京:科学出版社,2014.
[3] Gambardella L M,TaillardE,Agazzi G.MACS- VRPTW:A multiple ant colony system for vehicle routing problems with time windows[J].New Ideas in Optimization,1999:63-76.
[4] Gan R W,Guo Q S.Improved ant colony optimization algorithm for the traveling salesman problems[J].Journal of System Engineering and Electronics,2010,21(2):329-333.
[5] 杨浩雄,王 丹,张敬蕤.基于蚁群算法的拥堵交通最短路径研究[J].计算机仿真,2015(3):186-191.
[6] 陈迎欣.基于改进蚁群算法的车辆路径优化问题研究[J].计算机应用研究,2012(6):2031-2034.
[7] 张志协,曹 阳.基于改进型蚁群算法的最优路径问题求解[J].计算机系统应用,2012(10):76-80.
[8] 夏兰.基于蚁群算法的交通地理最佳路径的研究[D].武汉:武汉理工大学,2009.
[9] 张炳江.层次分析法及其应用案例[M].北京:电子工业出版社,2014.
[10] 边学丛,朱 婵,何衍兴.引入路径权重蚁群算法在应急救援中的应用[J].工业安全与环保,2010(11):60-62.
[11] 李彬何,宁韦昌.大城市客运交通方式的综合分析模型与应用[J]. 重庆交通学院学报,1997(2):67-72.
[12] 王 洪.基于MATLAB的应急救援最优路径选择[J].工业安全与环保,2009,35(1):48-50.
[13] 陈智宏.基于动态车辆导航系统的道路权重赋值方法研究[D].北京:北京工业大学,2006.
Research of Traffic Optimal Path Method Based onImproved Ant Colony Algorithm
Zhang Jirong,Yuan Xiaojie
(Communication and Information Engineering Institute, Xi′an University of Posts and Telecommunications,Xi′an 710061,China)
In view of the increasingly complex traffic networks,this paper proposes a traffic path optimal method based on improved ant colony algorithm, according to the idea of graph theory, first constructed the urban traffic network model, and combined with analytic hierarchy process to consider the road length, the stagnation of intersection, traffic congestion, road capacity and weather conditions, five main dynamic factors. Then, in the MATLAB platform, using the improved ant colony algorithm to solve the shortest path for static traffic and dynamic traffic networks respectively,finally has carried on the comparison and analysis.The research results show that under the influence of all kinds of traffic information, dynamic traffic network under the path optimization algorithm to find more accurate and more convenient route for travelers.
ant colony algorithm; dynamic traffic; optimal path
2015-12-02;
2015-12-31。
张继荣(1963-),女,辽宁沈阳市人,教授,硕士生导师,主要从事现代通信网方向的研究。
1671-4598(2016)06-0271-03
10.16526/j.cnki.11-4762/tp.2016.06.074
U491
A
