冗余捷联惯组故障诊断等价向量的补偿

王易南，任子君，陈朋印，闫 杰，陈 凯

(西北工业大学 航天学院，西安 710072)



冗余捷联惯组故障诊断等价向量的补偿

王易南，任子君，陈朋印，闫 杰，陈 凯

(西北工业大学 航天学院，西安 710072)

运载火箭作机动飞行时，陀螺和加速度计输出中引入的与机动状态相关的动态误差项会严重影响冗余捷联惯组故障诊断的效果，增大误警率；研究验证了利用卡尔曼滤波估计动态误差以补偿等价向量的方法，滤波补偿能够减弱由于运载火箭机动引起的动态误差项，利用补偿后的等价向量成功检测到未补偿时难以检测的故障；同时也发现了陀螺的补偿效果不如加速度计补偿效果好的现象；深入研究后发现，试验陀螺的随机误差偏大，掩盖了动态误差；得到了当传感器的随机误差项是动态误差项的5倍以上时可不进行误差补偿的有用结论。

冗余捷联惯组；故障诊断；等价向量；卡尔曼滤波；误差补偿

0 引言

对捷联惯组采用冗余备份技术和故障诊断技术是提高其可靠性的两种重要途径。冗余捷联惯组的故障诊断方法的快速性、准确性、实时性及可实现性是研究的难点。Kevin C Daly[1]等基于随机变量的似然估计提出了广义似然比法(GLT: Generalized Likelihood Test)；Hong Jin[2]等以对特定方向上传感器故障最敏感为性能指标，提出了最优奇偶向量法；Duk-Sun Shim[3]等基于矩阵的奇异值分解思想提出了冗余捷联惯组故障诊断的奇异值分解法。这些方法都是采用固定阈值来进行故障诊断。

由于捷联惯组存在测量误差，如：安装误差，刻度系数误差，常值偏差等。这些误差会对故障诊断带来影响，尤其是在运载火箭做机动飞行时，安装误差和刻度系数误差会产生随运载火箭机动而变化的误差项，严重干扰故障诊断的结果。Motyka等[4]和Robert等[5]等利用运载火箭机动的估计量，动态计算出阈值的方法来减小误差的影响。然而，在运载火箭作机动飞行时，动态阈值往往偏高，导致漏警率增大。因此，有必要采取措施将误差项补偿掉。Steven等[6]利用卡尔曼滤波器估计出陀螺的误差并补偿掉，收到了较好的诊断效果；张汉国等[7]利用分离偏倚估计的方法获得传感器误差的线性组合估计。本文以冗余捷联惯组故障诊断的GLT法[8]为基础，研究验证KF补偿传感器误差的方法，发现了陀螺的误差补偿效果不如加速度计误差补偿效果好的现象。深入研究后发现，陀螺的随机误差项占比较大，掩盖了其余的误差项，导致KF的补偿效果差。

1 传感器测量误差分析

惯性传感器(陀螺或加速度计)的测量输出中主要含有刻度系数误差、安装误差和常值漂移三种误差项，测量方程为：

(1)

式中，Z∈Rn×1是冗余测量值，n是传感器的个数，In是n阶单位阵，Hsf∈Rn×n是刻度系数误差矩阵，Hn∈Rn×3是测量矩阵，Hma∈Rn×3是安装误差矩阵，ω∈R3×1是运载火箭的惯性状态(三轴角速度或加速度)，b∈Rn×1是常值偏差值，ε∈Rn×1是随机噪声。

将式(1)展开：

(2)

由于误差项都是小量，因此，可忽略二阶小量得：

(3)

将Hma+HsfHn记为He，则测量方程可简记为：

(4)

利用广义似然比法[8]进行故障诊断时，等价向量为：

p=VZ=VHeω+Vb+Vε

(5)

可以看出，等价向量p是运载火箭状态ω、常值偏差b的函数。运载火箭的机动会导致故障判决函数超过给定的阈值，造成误警。

将式改写为：

(6)

式中，A=VHe，b1=Vb，ε1=Vε。

矩阵A和向量b1中的元素是传感器误差(刻度系数误差、安装误差和常值漂移)的线性组合，是待估量。

将Aω改写为Ωa，这里用到了矩阵中的拉直运算：

(7)

式中，→代表拉直运算，⊗代表张量积。这样，矩阵A的信息就进入了向量a中。得到：

(8)

ω的最小二乘估值为：

(9)

(10)

进而，式(6)可表示为：

(11)

将待估量a和b1增广成一个误差向量e：

(12)

式(11)可化为：

(13)

(14)

式(13)可以作为传感器误差信息线性组合e的测量方程。

一般情况下，陀螺的刻度系数误差、安装误差和常值漂移可以建模为随机常数：

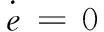
(15)

这样就得到了误差信息e的状态方程：

(16)

2 采用KF估计误差

由式(16)构成的线性离散系统，

状态方程：ek+1=ek

噪声统计特性：E(ε′(ε′)T)=σ2

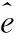
(17)

补偿后的等价向量p*只与随机噪声ε有关，而与运载火箭的惯性状态无关。利用补偿后的等价向量p*和GLT法进行故障诊断时，可采用固定阈值。

3 仿真试验

本文以6个单自由度陀螺的一种最优配置——正十二面体配置为例(图1)，研究误差补偿问题。

图1 惯组正十二面体配置

(18)

分别对陀螺和加速度计进行故障诊断仿真试验，试验的陀螺和加速度计的误差参数见表1所示。

首先研究无故障发生时的补偿效果。

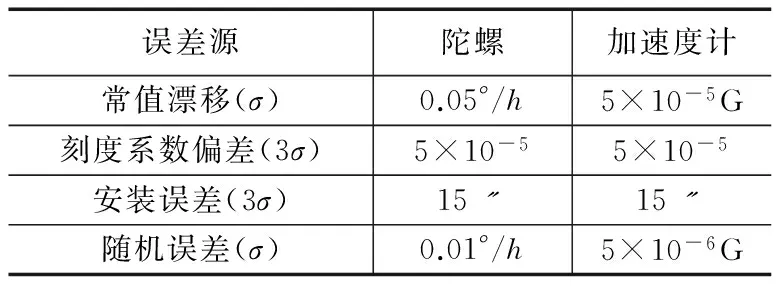
表1 捷联惯组误差模型参数

注：G为标准重力加速度。

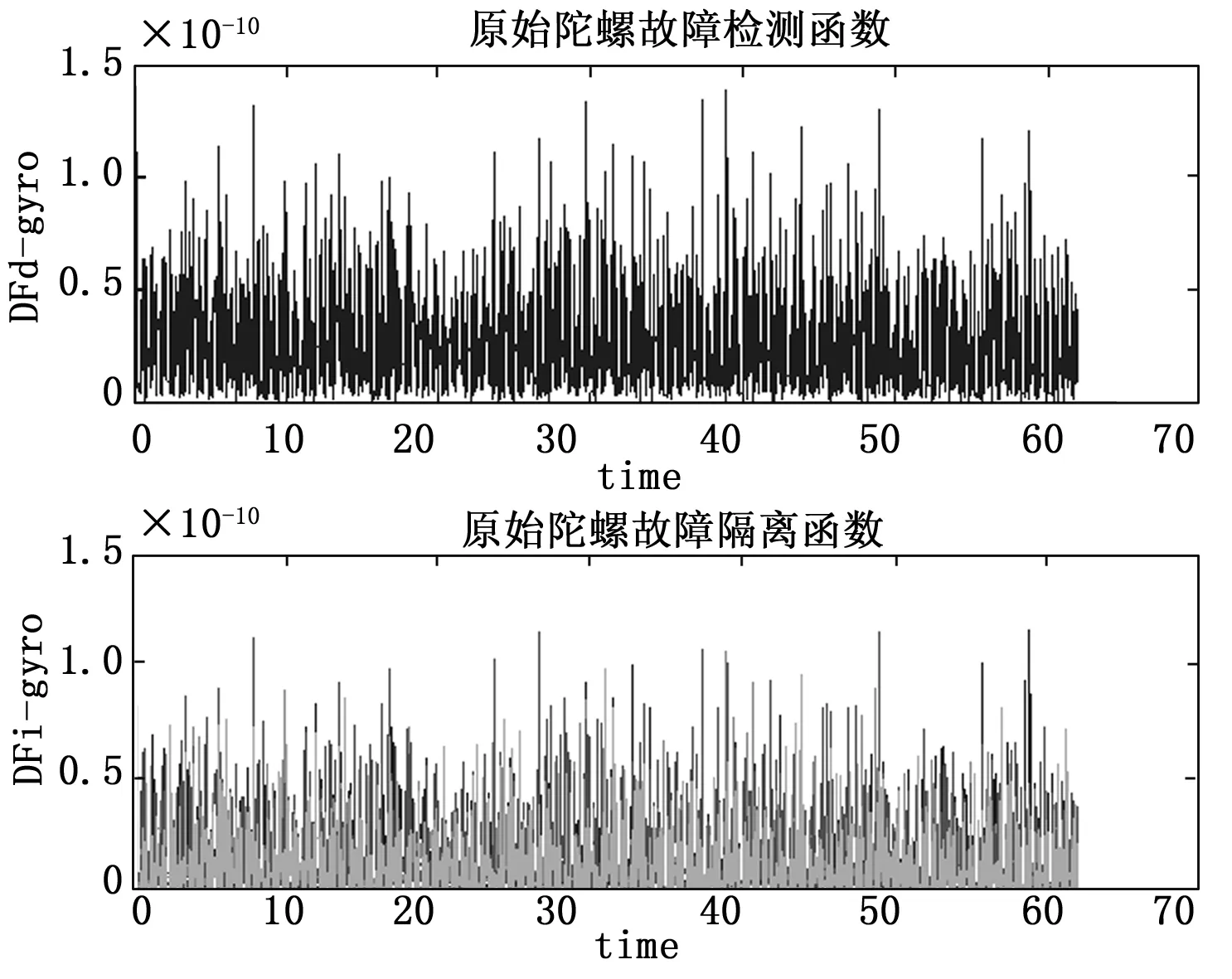
图2 无故障时，未补偿的陀螺故障诊断图

图3 无故障时，补偿后的陀螺故障诊断图

图4 无故障时，未补偿的加速度计故障诊断图

图5 无故障时，补偿后的加速度计故障检测图

由图2和图3可以看出，补偿前后，陀螺故障检测函数和隔离函数并没有太大变化。而图4和图5所示的加速度计的故障检测效果却发生很大变化：未补偿时，由于安装误差和刻度系数误差随运载火箭机动而变化，加速度计的故障检测函数也在不断变化；而补偿后的加速度计故障检测函数基本处于确定的水平，受运载火箭机动影响很小。

可以看出，对陀螺进行误差补偿收效不佳，没有对加速度计进行误差补偿的收效好。从节约计算资源的角度出发，可以只对加速度计进行误差补偿。

故障诊断试验在30s处，向1号加速度计注入0.5mG的阶跃型故障，未补偿时的故障检测效果如图6所示，在30s处，故障检测函数出现跳变，但这个跳变难以检测到。

而补偿后的检测效果如图 7所示，在30s处出现明显的阶跃跳变，跳变的幅值达到10-5量级，比无故障时的平均幅值高出两个量级，这使得故障很容易检测。同时，从图中也观察到，跳变衰减很快。这是由于卡尔曼滤波器试图吸收注入的故障，将故障归结为加速度计常值漂移误差项的变化。

图6 未补偿时，在30秒处向1号加计注入0.5 mG的阶跃故障

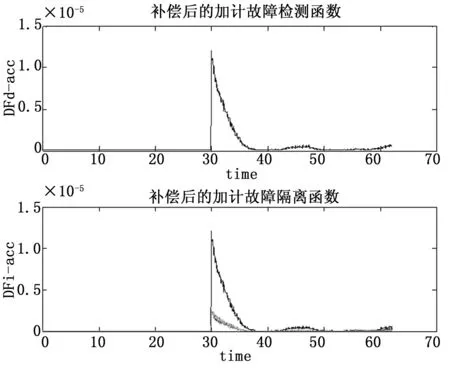
图7 补偿后，在30秒处向1号加计注入0.5 mG的阶跃故障

经仿真试验发现：由于陀螺和加速度计的误差组成有很大差别，两者的补偿效果也存在很大差别。

陀螺：由于陀螺的随机噪声项占绝对优势，掩盖了其余的误差项，滤波补偿效果较差。若人为地将陀螺的随机噪声降低5～10倍，则会出现较好的补偿效果。

加速度计：由于加速度计的随机误差项不占优势，滤波补偿效果较好。

当传感器的随机误差项是动态误差项(与运载火箭机动量、刻度系数误差和安装误差有关)的5倍以上时，可不进行误差补偿。

4 总结

安装误差和刻度系数误差会随着运载火箭机动而发生变化，这给故障检测带来了困难。本文研究了利用卡尔曼滤波器估计陀螺(加速度计)的误差参数的方法，减弱了由于运载火箭机动引起的误差量的变化，成功检测到未补偿时难以检测的小幅值故障。

但是，由于估计运载火箭惯性状态时采用的是最小二乘估计，当发生故障时，故障会逐渐污染最小二乘估计值，将故障引入到卡尔曼滤波器中，导致故障被滤波器吸收掉(表现为故障幅值的衰减)，对软故障的检测不利。一个可行的方法是利用运载火箭动力学模型或辅助导航设备估计出短时间内可信的运载火箭惯性状态。

[1]DalyKC,GaiE,HarrisonJV.GeneralizedLikelihoodTestforFDIinRedundantSensorConfigurations[J].GuidanceandControl, 1978, 2(1): 9-17.

[2]JinH,ZhangHY.Optimalparityvectorsensitivetodesignatedsensorfault[J].IEEETransactionsonAerospaceandElectronicSystems, 1999, 35(4): 1122-1128.

[3]ShimDS,etal.GeometricFDIbasedonSVDforredundantInertialsensorsystems[A]. 2004 5thAsianControlConference[C]. 2004.[4]MotykaPR,LandeyM,McKernR.FailuredetectionandisolationanalysisofaredundantstrapdowninertialmeasurementUnit[R].NASAContractorReport165658. 1981,2.

[5]Goodstein,RTse,BKWinkel,DJ.FailuredetectiontechniquefortheInertialupperstageredundantinertialnavigationsystem[A].AnnualAIAAGuidanceandControlConference[C].PaperNo.AIAA-82-1622-CP.

[6]StevenRH,MotykaP,GaiE,etal.In-flightparityvectorcompensationforFDI[J].IEEETrans.onAerospaceandElectronicSystems, 1983,AES-19(5): 668-675.

[7] 张汉国, 张洪钺. 改进的容错惯性导航系统[J]. 航空学报, 1990, 11(1)：A46-A52.

[8]DalyKC,GaiE,HarrisonJV.GeneralizedlikelihoodtestforFDIinredundantsensorconfigurations[J].GuidanceandControl, 1978, 2(1): 9-17.

Parity Vector Compensation for FDI in Redundant-IMUs

Wang Yinan, Ren Zijun, Chen Pengyin, Yan Jie, Chen Kai

(College of Astronautics, Northwestern Polytechnical University, Xi′an 710072，China)

The output of IMU contains dynamic errors, related to the maneuver state of the rocket, which influence negatively the fault diagnosis. The method is studied, that using Kalman filter to estimate the linear combinations of the dynamic errors to compensate the parity vector, which is used to make fault diagnosis decision. Simulations show that the method is successful. But the compensation result of accelerometers is better than the gyros’. The problem is solved by intensive research. The strong random noise of the gyros covers the dynamic errors, which makes the compensation results worse. Finally, a conclusion drawn that there is no need to compensate the parity vector, when random noise is 5 times more than dynamic errors.

redundant-IMUs; fault diagnosis; parity vector; Kalman filter; error compensation

2016-03-23；

2016-04-27。

航天支撑基金项目(2013HTXGD)。

王易南(1969-) ，男，北京人，博士，主要从事导航与制导系统设计方向的研究。

1671-4598(2016)06-0034-03DOI：10.16526/j.cnki.11-4762/tp

V

A