基于化学反应动力学耦合G方程的定容弹爆震燃烧研究

梁毅， 张玉银，， 李世琰， 徐斌

(1.上海交通大学机械与动力工程学院， 上海 200240；2.河南科技大学交通与车辆工程学院， 河南 洛阳 471000)



·性能研究·

基于化学反应动力学耦合G方程的定容弹爆震燃烧研究

梁毅1， 张玉银1，2， 李世琰1， 徐斌2

(1.上海交通大学机械与动力工程学院， 上海 200240；2.河南科技大学交通与车辆工程学院， 河南 洛阳 471000)

由于爆震受多方面的因素共同影响，且这些因素往往是相互耦合在一起，直接在内燃机上对各因素进行解耦进而研究单因素对爆震的影响几乎不可能。针对上述问题，首先基于化学反应动力学和G方程火焰面模型建立了长方体燃烧弹内的爆震燃烧三维CFD模型；然后在该模型基础上把初始压力、初始气温和初始壁温(末端)设为独立变量，系统地研究了各变量对正庚烷与空气混合气的爆震界限及爆震强度的影响。结果表明：当初始压力不高于0.25 MPa时，初始气温和末端壁温在300～700 K之间无论如何变化都不会发生爆震；当初始气温不高于450 K时，初始压力在0.2～0.5 MPa之间、末端壁温在300～700 K之间无论如何变化也都不会发生爆震。同时发现最大压力振幅可作为发生爆震与否的判据，本研究中只要最大压力振幅不高于0.02 MPa即不会发生爆震。

爆震; 定容燃烧弹; 化学反应动力学

对于内燃机来说爆震(Knocking,又称Deflagration)是一种非正常燃烧现象[1]。实践表明，严重的爆震会影响整个内燃机的性能，甚至对内燃机造成不可挽回的机械破坏。

鉴于爆震现象对内燃机的危害，学者对爆震现象做了很多的研究工作[2-6]。1968年，Affeleck等指出任何影响末端气体传热的因素都对爆震产生影响[2]；2006年何鑫等在快速压缩机上进行了高速摄影试验，结果显示燃料的摩尔分数是决定自燃模式的关键因素[3]；2007年M. Poschl等在快速压缩机上进行研究，发现引起爆震的主要因素是温度分布的不均匀性，且不同的分布情况会导致不同程度的爆震[4]；2011年Zahdeh等直接在内燃机上研究进气温度、压缩比和增压比等多个因素对爆震的影响，结果表明进气温度的提高会导致末端混合气更容易发生自燃[5]；2013年王志等在直喷汽油机上针对高负荷下的爆震进行试验研究，证实了降低进气门关闭时的缸内气体温度可抑制爆震[6]。然而，上述对爆震现象的研究均是直接在内燃机或者快速压缩机上实现的，导致直接在内燃机上对影响爆震且相互耦合的各因素进行解耦分析，研究单一因素对爆震的影响几乎是不可能的。但是，单一因素对爆震界限及爆震强度的影响对于探究爆震燃烧机理和抑制内燃机爆震又是非常重要的。

为了克服以往工作的不足，本研究设计了一种可以对影响内燃机爆震的因素进行解耦分析的长方体爆震燃烧弹(以下称为长方体燃烧弹)，该长方体燃烧弹可以把初始混合气温度、压力、初始末端壁面温度解耦。基于化学反应动力学耦合G方程建立了该长方体燃烧弹内的三维CFD模型，研究了初始混合气温度、压力、初始末端壁面温度分别作为单一因素变化时对爆震燃烧的影响规律，并获得发生爆震与否的界限。本研究将为该类燃烧装置的设计与优化和内燃机抑制爆震燃烧提供理论依据。

1 模型建立与验证

1.1 长方体燃烧弹仿真模型建立

本研究通过Converge软件建立三维CFD的长方体燃烧弹仿真模型。采用燃烧室为20 mm×20 mm×100 mm的小型卧式长方体燃烧弹实现各因素分离，在固定其他因素不变的情况下，研究单一因素对爆震的影响。长方体燃烧弹外形见图1a，燃烧室见图1b，其中A点为末端混合气压力(以下称为末端压力)数据采样位置，距离末端壁面1 mm。

为了捕捉到爆震时的快速燃烧过程，末端压力采样时间间隔为5×10-6s。火花塞布置在长方体燃烧弹的B点位置(见图1b)，距离右端壁面5 mm，点火时燃烧室内为化学当量比的正庚烷(C7H16)与空气均质混合气，且混合气温度均匀、无压力间断。本研究分别采用两个热点模拟实际火花塞点火时的电容放电和电感放电过程，总能量为500 mJ的高能量点火。考虑到既要节约计算成本又要保证计算的精度，采用笛卡尔网格，初始网格设置为2 mm ×2 mm×2 mm，计算过程中程序根据温度梯度和速度梯度自适应加密到最小网格边长0.5 mm，点火附近则固定加密到0.125 mm。有关网格设置参考了Yang[11]等建立的模型。

长方体燃烧弹燃烧室壁面温度的设置参考了实际汽油机的燃烧室、活塞顶壁面温度值。Nakagawa等通过试验发现自燃始于燃烧室壁面，因此，初始末端壁面温度(以下称为末端壁温，Tw)可能是爆震重要的影响参数之一，本研究把末端壁温设为变量[12]。燃烧室靠近A点的端面为离末端混合气最近的壁面(类似排气门顶面，相当于实际内燃机中的局部热点)。除末端壁面外，其他壁面温度与汽油机正常运行时气缸壁面温度相当，设置固定值440 K(见图1b)。

本研究将系统地研究初始混合气温度(以下称为初始气温，Tg)、初始混合气压力(以下称为初始压力，pi)和末端壁温作为单一变量变化对爆震界限及爆震强度的影响。

图1 长方体燃烧弹仿真模型

1.2 长方体燃烧弹仿真模型验证

为了保证该长方体燃烧弹仿真模型模拟的可靠性，对模型中的化学反应机理、子模型(如燃烧模型、湍流模型等)及其参数设置的正确性进行了验证。

参考Tinaut等的试验结果，利用与长方体燃烧器模型一致的化学反应机理、子模型及其参数设置建立了球形燃烧器三维CFD模型[13]。Tinaut的试验是在直径为200 mm的球形燃烧器上进行，基本参数见表1[13]。在球形燃烧器中压力随时间变化的实测值与本研究计算值的比较情况见图2，CFD仿真模型模拟压力和试验结果基本吻合，说明球形燃烧器的三维CFD仿真模型基本上能正确反映出试验时的燃烧特性，从而验证了长方体燃烧弹仿真模型的子模型及其参数设置具有充足的可靠性，可用于进一步的燃烧过程模拟研究。

表1 球形燃烧器初始参数

图2 燃烧器压力仿真值与试验值的对比

2 结果分析

参考实际汽油机发生爆震时的缸内环境，考虑到长方体燃烧弹火花点火后形成的火焰沿长轴方向传播时压力升高，未燃混合气不断受到压缩，这个过程可以看作汽油机内活塞的压缩过程。长方体燃烧弹内爆震发生前的压力与汽油机压缩终了的压力相当，如果把初始压力设置在0.4 MPa，爆震前的压力大约为2 MPa。本研究的初始压力设置为0.2～0.5 MPa，最小间隔为0.05 MPa。自然吸气汽油机进气温度较低，而增压并引入EGR的汽油机进气温度较高，本研究中把初始气温设置在300～700 K之间，间隔为50 K。排气门顶面温度在冷起动时较低，而在正常运行一段时间后温度又很高，因此将末端壁温设在300～700 K之间，间隔为50 K。

2.1 爆震评价指标

为了定量分析爆震，需要确定爆震的评价指标，判定是否发生爆震及爆震强度。Oppenheim[14]给出了较全面的爆震定义：爆震是一种特殊的燃烧方式，它是自发和随机地产生，导致锐利的压力脉冲。本研究提出以长方体燃烧弹内末端混合气(图1b中的A点)的最大压力振幅作为爆震评价指标。最大压力振幅定义为燃烧室末端压力与平均压力之差的绝对值的最大值，平均压力为燃烧室内腔压力平均值。

图3和图4分别示出了长方体燃烧弹内爆震与非爆震工况下的压力变化情况。由图可知，发生爆震时末端压力出现剧烈的压力振荡，压力振幅曲线存在多个压力脉冲；而非爆震工况下则不出现剧烈的压力振荡，压力振幅曲线中不存在压力脉冲。

图3 爆震工况压力曲线

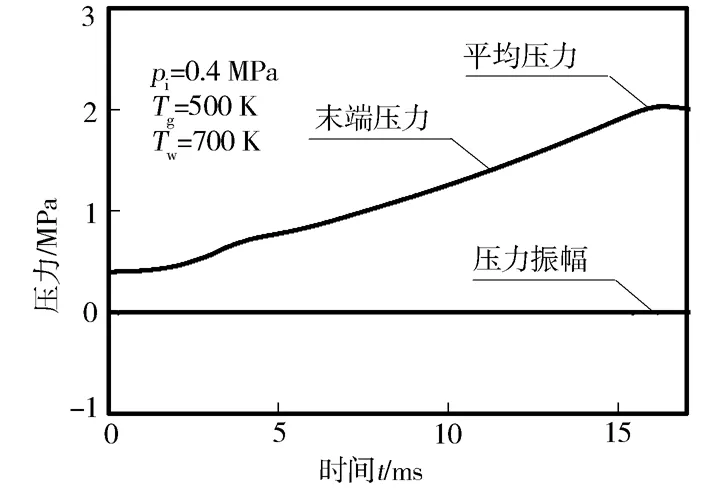
图4 非爆震工况压力曲线

图5示出了爆震与非爆震工况下长方体燃烧弹燃烧室内火焰的温度分布对比。由图5可看出，火花点火形成的火焰面往前推进一段时间后，火焰前锋面呈郁金花状向前传播，将燃烧室划分为己燃区和末燃区；初始气温700 K工况中的末端混合气从7.82 ms开始发生自燃，同时，图3中长方体燃烧弹的末端压力开始出现剧烈振荡，这是由于爆震压力波在燃烧室内来回反射的结果。显然，明显的压力振幅标志着爆震的开始，因此采用最大压力振幅来评价爆震开始是合理的，后面还将进一步说明用最大压力振幅作为判定是否发生爆震和爆震强度的依据。

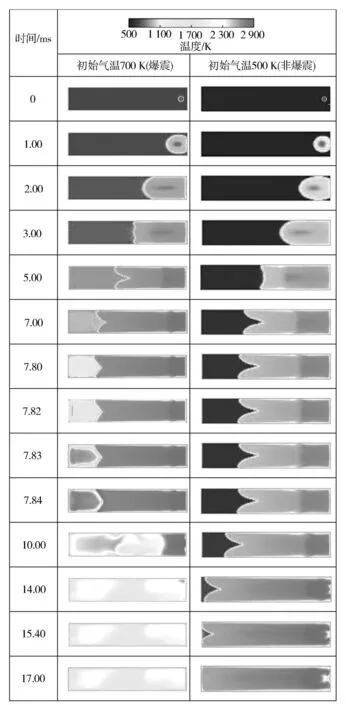
图5 爆震与非爆震工况长方体燃烧弹燃烧室内温度分布

2.2 初始压力对爆震的影响

为了研究初始压力对爆震燃烧特性的影响，在同一末端壁温、初始气温条件下选取不同的初始压力进行计算。长方体燃烧弹的初始参数见表2。

表2 初始压力的变化范围

初始压力对爆震压力波的影响见图6。图6表明：在初始压力不超过0.25 MPa的工况，末端压力不出现明显振荡；在初始压力为0.3 MPa及更高的工况时，随初始压力提高，爆震时刻明显提前，压力振幅明显增大。

图6 初始压力对爆震压力波的影响

初始压力对爆震强度的影响见图7。从图7可以看出：初始压力在0.3～0.5 MPa之间变化时，随初始压力提高最大压力振幅快速增大。结合图6和图7可知：初始压力为0.25 MPa，0.2 MPa时末端压力无明显的振荡，不发生爆震，最大压力振幅均不大于0.004 MPa；初始压力不低于0.3 MPa时末端压力有明显的振荡，发生爆震，最大压力振幅均不小于0.24 MPa，且初始压力越高，末端压力振荡幅度越大，爆震越强烈，对应的最大压力振幅越大。显然，以初始压力作为单一变量，爆震与非爆震的工况点的最大压力振幅分别在两个数量级上。这里取最大压力振幅0.02 MPa为阈值，认为最大压力振幅超过0.02 MPa时为爆震，小于0.02 MPa时为非爆

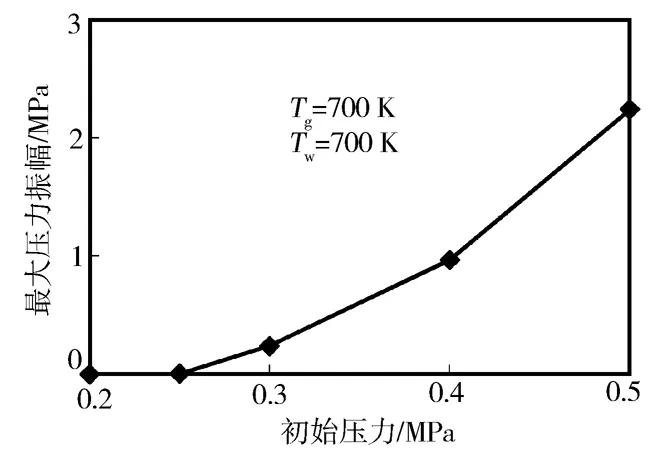
图7 初始压力对爆震强度的影响

震, 并认为压力振幅首次达到0.02 MPa时刻为爆震时刻，且最大压力振幅越大爆震越强烈。因此，使用最大压力振幅来判定爆震强度是合理的，后续结果也将证实这一判据的合理性。

2.3 初始气温对爆震的影响

为了研究初始气温对爆震燃烧特性的影响，在同一末端壁温、初始压力条件下选取不同的初始气温分布点进行研究。初始气温变化时长方体燃烧弹的初始参数见表3。

表3 初始气温的变化范围

初始气温对爆震压力波和末端压力的影响见图8。图8表明：当初始气温不超过500 K时，末端压力不出现明显振荡，上升平缓；当初始气温达到550 K时，随初始气温提高，爆震时刻明显提前，压力振幅明显增大。

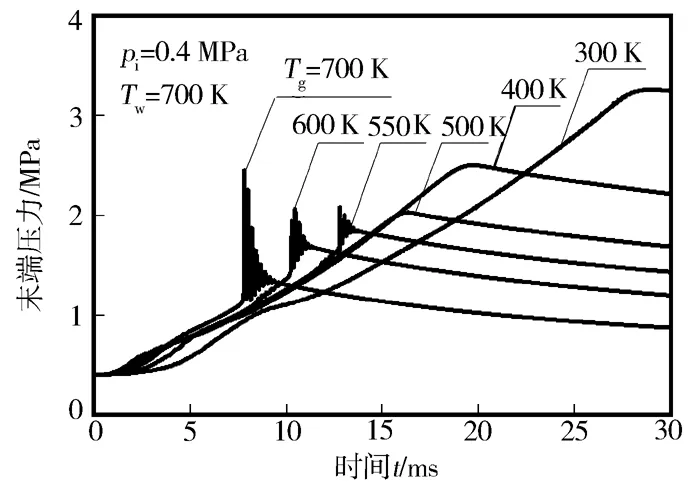
图8 初始气温对爆震压力波的影响

初始气温对爆震强度的影响见图9。从图9可以看出：初始气温在500～700 K之间变化时，随初始气温提高最大压力振幅快速增大。结合图8和图9可知：初始气温低于或等于500 K时末端压力无明显的振荡，不发生爆震，最大压力振幅均不大于0.016 MPa；当初始气温高于500 K时末端压力有明显的振荡，发生爆震，最大压力振幅均不小于0.18 MPa。显然，以初始气温作为单一变量时，最大压力振幅阈值0.02 MPa可以用于判断爆震与否，且最大压力振幅越大爆震越强烈。

图9 初始气温对爆震强度的影响

2.4 末端壁面温度对爆震的影响

为了研究末端壁温对爆震燃烧特性的影响，在同一初始气温、初始压力条件下选取不同的末端壁温分布点进行研究。末端壁温变化时长方体燃烧弹的初始参数见表4。

表4 末端壁温的变化范围

末端壁温对爆震压力波的影响见图10。图10表明：末端壁温不超过450 K时，各工况下末端混合气的压力曲线变化不大；末端壁温升高到500 K及以上时，末端压力出现明显的振荡。

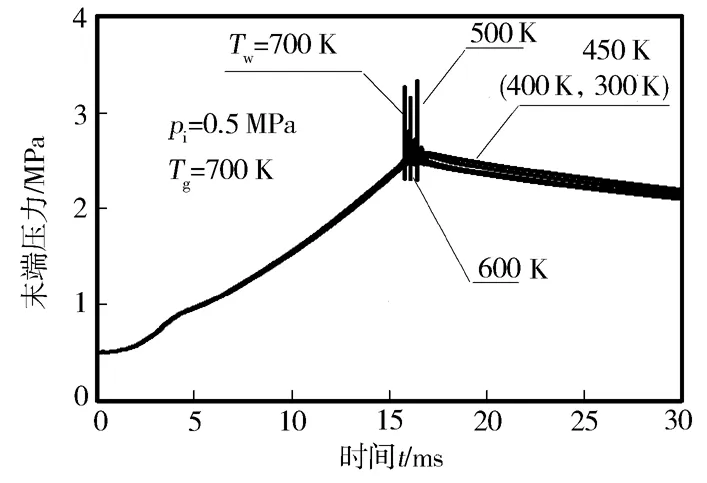
图10 末端壁温对爆震压力波的影响

末端壁温对爆震强度的影响见图11。从图11可以看出：末端壁温在450 K及以下时，最大压力振幅均较小(不超过0.01 MPa)；末端壁温为500 K及以上时，最大压力振幅均较大(不低于0.59 MPa)。

结合图10和图11可知，末端壁温为450 K及以下时末端压力无明显的振荡，不发生爆震，最大压力振幅均不大于0.008 MPa；末端壁温在500 K及以上时末端压力出现明显的振荡，发生爆震，最大压力振幅均不小于0.59 MPa。显然，以末端壁温作为单一变量时，最大压力振幅阈值0.02 MPa可以用于判断爆震与否，且最大压力振幅越大爆震越强烈。

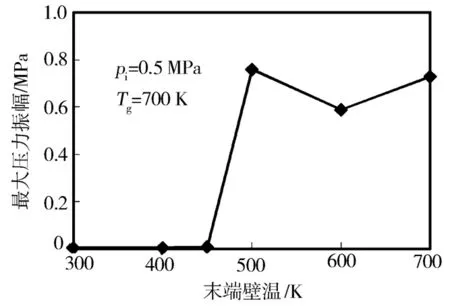
图11 末端壁温对爆震强度的影响

2.5 爆震阈值与极限

上述仿真计算结果表明：在所有非爆震工况中，最大压力振幅均小于0.02 MPa；在所有爆震工况中，最大压力振幅均大于0.02 MPa。因此，判断爆震与否的依据可以采用最大压力振幅，认为最大压力振幅超过0.02 MPa为爆震，最大压力振幅越大爆震越强烈，同时，爆震开始时刻可以从压力振幅首次达到0.02 MPa时判定。

通过上述阈值获得了爆震界限(见图12)，本研究计算点均在黑色线围成的四方体框图内。从图12可以看出：当初始压力不高于0.25 MPa时，初始气温和末端壁温在300～700 K范围内不管怎样变化都不会发生爆震；在初始气温不高于450 K时，初始压力在0.2～0.5 MPa之间、末端壁温在300～700 K范围内无论如何变动也都不会发生爆震。因此，初始压力和初始气温是决定爆震与否的主要因素，而末端壁温对爆震界限的影响相对较小。

图12 爆震界限

3 结论

a) 初始压力和初始气温是决定爆震与否的关键因素，末端壁温对爆震界限的影响相对较小;当初始压力不高于0.25 MPa时，初始气温和末端壁温在300～700 K范围内无论如何变化都不会发生爆震；当初始气温不高于450 K时，初始压力在0.2～0.5 MPa范围、末端壁温在300～700 K范围内无论如何变化时都不会发生爆震;

b) 随着初始压力、初始气温提高，爆震时刻提前，爆震强度(最大压力振幅)增大;

c) 判断爆震与否的依据可以采用最大压力振幅，本研究中最大压力振幅在0.02 MPa以上时发生爆震；爆震与非爆震时的最大压力振幅相差一个数量级以上。

[1] 武得钰, 顾笑映, 李继军, 等. 火花点火发动机爆震燃烧研究的发展与现状 (Ⅰ)[J].车用发动机,1995(5):1-6.

[2] Affleck W S, Fish A. Knock: Flame Acceleration or Spontaneous Ignition[J].Combustion and Flame,1968,12(3):243-252.

[3] Walton S M, He X, Zigler B T, et al. An Experimental Investigation of Iso-octane Ignition Phenomena[J].Combustion and Flame,2007,150(3):246-262.

[4] Poschl M, Sattelmayer T. Influence of Temperature Inhomogeneities on Knocking Combustion[J].Combustion and Flame,2008,153(4):562-573.

[5] Zahdeh A,Rothenberger P,Nguyen W,et al. Fun-damental Approach to Investigate Pre-Ignition in Boosted SI Engines[J].SAE Paper 2011-01-0340.

[6] 王志，徐雅齐，王建昕，等.增压直喷汽油机扫气抑制爆震试验研究及模拟解析[J].内燃机工程,2013,34(4):13-17.

[7] Liang L,Reitz R D, Iyer C O, et al.Modeling knock in spark-ignition engines using a G-equation combustion model incorporating detailed chemical kinetics[C].SAE Paper 2007-01-0165.

[8] LIU Yaodong,JIA Ming,XIE Maozhao,et al. En-hancement on a skeletal kinetic model for primary reference fuel oxidation by using a semidecoupling methodology[J].Energy & Fuels,2012,26(12):7069-7083.

[9] Han Z, Reitz R D.Turbulence Modeling of Internal Combustion Engines using RNG κ-ε Models[J].Combustion Science and Technology,1995,106(4-6):267-295.

[10] Han Z,Reitz R D.A Temperature Wall Function Formulation for Variable-density Turbulent Flows with Application to Engine Convective Heat Transfer Modeling[J].International Journal of Heat and Mass Transfer,1997,40(3):613-625.

[11] Yang X,Solomon A,Kuo T W. Ignition and combustion simulations of spray-guided SIDI engine using Arrhenius combustion with spark-energy deposition model[C].SAE Paper 2012-01-0147.

[12] Nakagawa Y,Takagi Y,Itoh T.Laser shadow graphic analysis of knocking in SI engine[C].SAE Paper 845001,1984.

[13] Tinaut F V,Reyes M,Giménez B, et al. Measurements of OH and CH Chemiluminescence in Premixed Flames in a Constant Volume Combustion Bomb under Autoignition Conditions[J].Energy & Fuels,2010,25(1):119-129.

[14] Oppenheim A K. The knock syndrome-its cures and its victims[C].SAE Paper 841339,1984.

[编辑: 李建新]

Knock Combustion of Constant Volume Bomb Based on Chemical Kinetics Coupling G-equation

LIANG Yi1, ZHANG Yuyin1,2, LI Shiyan1, XU Bin2

(1.School of Mechanical Engineering, Shanghai Jiaotong University, Shanghai 200240, China; 2. School of Vehicle and Transportation, Henan University of Science and Technology, Luoyang 471000, China)

It was extremely difficult to analyze the effect of single factor on knock due to the collective action and mutual coupling of knock influencing factors. For the above problem, a 3D CFD model of knock combustion in a rectangular constant volume bomb was built based on the chemical kinetics and G-equation flame model. Then the influence of single variable such as initial pressure, initial mixture and wall temperature on knock limit and intensity of n-heptane and air mixture was researched systematically. The results show that the knock will not occur when the initial temperature of mixture and wall is between 300 K and 700 K and the initial pressure is lower than 0.25 MPa; and when the initial temperature of mixture is lower than 450 K, the initial temperature of wall is between 300 K and 700 K and the initial pressure is between 0.2 MPa and 0.5 MPa. Besides, the maximum fluctuation amplitude of pressure can be used as knock criterion and its upper limit is 0.02 MPa.

knock combustion; constant volume bomb; chemical kinetics

2016-01-11;

2016-01-31

内燃机燃烧学国家重点实验室开放基金资助项目(K2014-2)；上海市教育委员会科研创新项目(14ZZ022)

梁毅(1988—)，男，硕士，主要研究方向为爆震燃烧过程；liangyisjtu@126.com。

通讯简介： 张玉银(1962—)，男，教授，博士，主要研究方向为喷雾燃烧及发动机燃烧过程等；yuyinzhang@sjtu.edu.cn。

10.3969/j.issn.1001-2222.2016.02.004

TK411.22

B

1001-2222(2016)02-0017-06