基于异向波速模型的微震定位改进

戴峰， 郭亮， 徐奴文,2*， 樊义林, 徐剑， 姜鹏

1 四川大学 水力学与山区河流开发保护国家重点实验室， 成都 610065 2 山东大学 土建与水利学院， 济南 250061 3 中国长江三峡集团公司， 北京 100038



基于异向波速模型的微震定位改进

戴峰1， 郭亮1， 徐奴文1,2*， 樊义林3, 徐剑3， 姜鹏1

1 四川大学 水力学与山区河流开发保护国家重点实验室， 成都 610065 2 山东大学 土建与水利学院， 济南 250061 3 中国长江三峡集团公司， 北京 100038

针对波速分层的区域岩体，在异向波速模型的基础上，对垂向上的应力波按岩体波速值大小作分段区别，推导震源应力波走时关系式，建立分层速度定位目标函数，基于此提出一种由参数准备、层速度反演、微震定位三个模块组成的分层速度定位模型SV，并采用遗传算法进行优化求解.然后，对分层速度定位模型在已构建微震监测系统的白鹤滩水电站左岸岩质边坡进行验证.微震事件重定位结果表明，分层速度定位模型定位微震事件的最大、最小和平均偏离层内错动带程度指标较单一速度模型分别降低了57.17%、36.51%和57.35%，证明了定位模型在波速分层的区域岩体微震定位应用中比单一速度定位模型更加合理可靠.

微震监测； 异向波速模型； 分层速度定位模型； 遗传算法； 岩质边坡

The SV model is proposed based on the anisotropic velocity model, which simplifies the propagation path of stress waves into a straight line, which consists of horizontal and vertical velocities, that is, one for underground sensors and the other for surface sensors. Taking into account that the vertical stress waves pass through some rock formations at different velocities, the model is constructed part by part according to the values of each interval velocity. The first thing is to derive the nonlinear equation of stress wave travel time by spatial analytic geometry′s operation and analysis. The target function of SV is established by using L2 norm of the time residual between the measured value and calculated value of the travel time difference of each two sensors. Secondly, based on the established target function, the SV is proposed, which consists of parameters-preparation module, interval velocities inversion module and seismic location module. In the parameters-preparation module, the regional rock mass is divided into some wave-velocity layers according to engineering geological data. And, using spatial analytic geometry′s operation and analysis, the analytical expressions for layer interfaces are derived. In the interval velocities inversion module, the target function to solve velocities is figured out according to the form of the target function of SV. Then we collect some blast events or rockburst with known coordinate values. Using the genetic algorithm (GA), we can get optimization solutions of velocities. In the seismic location module, using the determined velocities, the target functions to locate MS events are figured out according to the form of the target function of SV as well. It should be emphasized that during the optimal solving, for every wave-velocity layer, the concrete forms of target function and searching regions are different from each other. Using GA, the optimization solutions of a MS event for each wave-velocity can be worked out, and the minimum of optimization solutions is considered to be the location of one MS event.

In order to verify the effectiveness and reliability of SV, we applied it to a slope engineering on the left bank of the Baihetan hydropower station, where a MS monitoring system (ESG, from Canada) has been installed. Firstly, the slope was divided into 11 wave-velocity layers, which included 4 kinds of velocities, according to the sonic wave testing given by engineering geological investigation data. And, the analytical expressions for layer interfaces were worked out. Secondly, we collected 4 blast events that occurred at 610 m-elevation irrigation and drainage galleries. Using GA, we got optimization solutions of velocities, which are 4500 m·s-1, 4900 m·s-1, 3750 m·s-1, 5000 m·s-1, respectively, through minimizing the target function. And then, 11 target functions to locate MS events for each wave-velocity were figured out by using the determined velocities and parameters of layer interfaces. The MS events were collected from 1 to 18, April, 2015. The locations of these MS events were determined by using the simplified single-velocity model, of which the velocity is 4600 m·s-1(approximate mean value of 4 velocities above). Finally, those MS events, which were scattered around two dislocation bands (LS331, LS337), were relocated by using the SV. The relocation results show that the maximum, minimum and average deviations from dislocation bands decrease by 57.17%, 36.51% and 57.35%, respectively. It is clear that SV is more convenient and reliable than the single velocity location model aimed at those regional rock masses with stratified velocities.

The improved location model (SV), which is based on the anisotropic velocity model, takes into account the impact from the different velocities of rock formations with different lithological characters. Compared with the single velocity model, the accuracy of MS events location aimed at the regional rock masses with stratified velocities is improved obviously. However, like all MS events location models, it requires an accurate velocity-distribution of regional rock masses. Further study on improving the accuracy of MS events location can be achieved through considering velocity partitions inside each rock formation and finding a stable location model, which is more suited to the calculation of the actual stress wave traveltimes.

1 引言

岩石在外界应力作用下，其内部将产生局部弹塑性能集中现象，当能量积聚到某一临界值之后，就会引起岩体微裂隙的产生与扩展，微裂隙的产生与扩展伴随着弹性波或者应力波的释放并在周围岩体内快速传播，这种弹性波在地质上称为微震(microseismic/acoustic emission)(Xu et al.，2011).微震现象是由美国矿业局Obert(1977)发现，后来Kaiser(1950)对该现象命名为Kaiser效应.微震监测技术是通过在监测区域岩体布置检波器或者传感器来收集微震信号，然后分析该信号以圈定岩体损伤区域，从而为区域岩体稳定性评价提供有效依据.如今，微震监测分析技术作为工程建设安全预测预警方法被广泛应用到矿山开采(姜福兴等，2006；陆菜平等，2010)、石油开采(宋维琪等，2015)、水利水电工程(Xu et al.，2011；张伯虎等，2012)等行业.

为了使微震监测技术更好地发挥预测预警作用，满足工程需求，定位精度的提高至关重要.微震定位问题属于地球物理反演问题，它根据一次微震事件在各传感器的震相到时来反演微震的发生时刻和空间位置(Spencer and Gubbins，1980；Pavlis and Booker，1980；刘福田，1984；刘杰等，2003；高永涛等，2015).但是，在实际工程应用中，由于区域岩体是非均匀各向异性介质，同时岩体中存在不同走向和倾角的节理断层，微震震源发出的应力波在传播过程中能量、频率和波速改变，这都给微震定位精度带来了较大的影响.为了实现高精度微震定位，需要采用合理的传感器空间布置方案、有效的微震波形识别技术以及合适的微震定位方法.

微震定位方法主要有几何作图法、相对定位法、空间域定位法、线性定位法和非线性定位法.几何作图法是一种直观的定位方法，依据走时方程，通过二维或者三维作图确定震源位置(廉超等，2006).相对定位法又称为主事件定位法，是根据一个震源坐标较精确的主事件来计算其附近其他微震事件的坐标(Spence，1980).空间域定位法是由距离残差代替到时残差的一种定位方法.微震震相到时和震源参数的关系是一种非线性关系.线性定位法是通过求导、级数展开方法将该非线性问题转化为线性问题的定位方法，例如Inglada(1928)法和Usbm(1970)法.这类方法在到时拾取精度不高的情况下定位效果较差.非线性定位法是利用迭代或优化求解方式的定位方法统称，例如Thurber(1985)用非线性牛顿迭代法进行定位.随着计算机计算能力不断发展，不同的非线性优化算法工具被应用到定位中，用于算法优化的目标函数也出现了不同的形式.赵珠和曾融生(1987)在定位中采用了单纯形法.但是单纯形法采用单向搜索，形式简单，容易陷入局部最优解.针对这一缺点，全局最优化算法被应用到定位中，王洪体等(2006)介绍了一种基于浮点遗传算法的定位方法，具有稳定收敛、精度高、时效性强的特点；张华等(2014)基于遗传算法对厂矿区内的人工爆破进行定位，得到了很好的效果；针对速度模型给不准和联合定位法震源位置、发震时刻和微震传播速度相互关联，解不唯一的问题，陈炳瑞等(2009)提出微震震源定位分层处理方法，并采用粒子群算法进行优化求解；董陇军等(2011)针对单一速度模型提出了无需预先测速的微震震源定位方法，利用非线性拟合工具进行求解；李健等(2014)针对单一速度模型，提出了无需测速的定位方法，采用单纯形法进行最优化求解.上述定位算法多是建立在单一速度模型的基础上.虽然实际岩体中不同区域和方向上的波速值不尽相同，但是单一速度模型因不考虑太多未知量和关系，计算稳定性强，是最常见的一种速度模型.

近几年，一些专家和学者在寻找适应各种区域岩体微震定位的速度模型上做出了不同探索.一般情形下，某个微震定位算法速度模型的优劣取决于两点：(1)是否可以较好地考虑区域岩体的波速特性，且能够给出恰当的应力波传播路径；(2)是否简洁，从而利于算法稳定实现(Feng et al.，2015).射线追踪理论能够找到复杂岩体中应力波传播路径，从而逐渐被应用到波速差异大、带空洞的区域岩体微震定位中(Bai and Greenhalgh，2006；Bai et al.，2010；Collins et al.，2014；Hosseini et al.，2015).但是，复杂岩体的速度模型建立及射线追踪的实现对计算机要求相当高，计算耗时大且不利于算法稳定地实现.为此，一些专家和学者针对不同波速分布特征的区域岩体分别对应力波传播特性作了相应简化处理，在提高定位精度的同时保证了计算的稳定性.其中，Feng等(2015)针对隧洞开挖工程中围岩波速特征，提出按隧洞断面对传感器进行波速值分组的定位速度模型，考虑了开挖隧洞中各断面波速值差异，同时采用粒子群算法对所建立的目标函数实现稳定求解；巩思园等(2012)针对煤矿上覆岩层多以层状形式赋存，P波在垂向和水平向的速度及传播路径差异大的情况，提出建立“异向波速模型”，模型求解选用遗传算法与CMAES (Covariance Matrix Adaptation Evolution Strategy，协方差矩阵自适应进化策略)算法结合的混合算法，经验证定位效果优于单一速度模型.

本文综合分析各种非线性定位方法，在“异向波速模型”基础之上，将垂向上的应力波按各岩层波速值大小进行分段处理，提出一种简化的分层速度定位模型SV.该定位模型在考虑了不同岩层应力波波速值大小不同的基础上，对复杂的层间应力波传播路径进行了简化处理，采用具有全局寻优特性的遗传算法对建立的分层速度目标函数稳定求解.相比单一速度定位模型，在波速分层的区域岩体微震定位中有利于定位精度的提高.

2 传统单一速度定位模型

微震发生时向周围岩体释放纵波(P波)和横波(S波)，前者传播速度比后者快.当传播距离足够远时，在波形图中能够将P波与S波起跳时刻区分开来.然而，对于微震监测区域来说，由于监测区域不大，往往S波的起跳点叠加在P波中，要精确拾取S波初至时刻很困难.因此，通常仅拾取P波初至时刻用于定位.

对于单一速度模型，第i个传感器接收P波初至时刻ti与震源参数(x0，y0，z0，t0)之间的关系由(1)式表述：

(i=1，2，…，m)

(1)

式中：li为震源与第i个传感器之间的空间距离；(xi，yi，zi)为第i传感器空间坐标，m是监测区域内接收到P波的传感器数量；V为监测区域P波波速值.

理论上，微震事件发生时刻与走时之和t0+Δti应同ti相等，即

(2)

但是，在实际工程应用中，由于受到监测仪器以及人为因素的影响，微震信号起跳时刻的拾取存在误差，则ξi值不为零.在这样的情况下，为了实现微震震源定位，需使用非线性优化工具进行最优化求解来逼近真值.通常单一速度定位模型采用的非线性优化目标函数有如下三种形式：

因变量为到时的目标函数：

(3a)

因变量为到时差的目标函数：

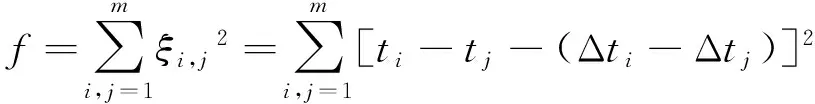
(3b)

因变量为到时差商的目标函数：

或

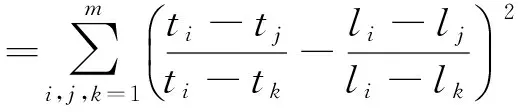
(3c)

运用非线性优化方法，得到使上述目标函数尽量小的震源参数逼近解作为微震震源参数的最终计算结果.其中，第一种目标函数(3a)能将震源发生时刻一起反演；第二、三种目标函数(3b)、(3c)不能反演震源发生时刻；第一、二种目标函数(3a)、(3b)含有岩体波速参数，在优化求解过程中可以与震源参数一起反演，从而实现均匀波速模型下无需预先测速的微震定位(董陇军等，2011)；第三种目标函数(3c)不含岩体波速参数，从而能够实现均匀波速模型下的无需测速微震定位(李健等，2014).

3 异向波速模型的改进

在实际工程中，微震监测区域岩体并不是均匀介质，不同区域的应力波波速不同.因此，应力波射线是按最小走时路径传播，而并非几何最短路径.在许多工程中，岩体呈层状分布，例如层状矿层、层状边坡.

在层状煤矿微震监测中，震源应力波传播到矿区地面的检波器比到井下巷道经过的岩体介质更为复杂，导致P波在垂向上速度变化很大.针对煤矿中这种层状赋存和离层带的特点，巩思园等(2012)提出对安装在井下巷道和矿区地面的检波器进行区别对待，采用两种速度建立异向波速模型：针对井下的检波器，岩体波速较为均匀，P波传播最小走时路径近似为最短路径传播，速度为Vi=Vpu；针对矿区地表的检波器，将实际最小走时路径(折线)简化为最短路径，速度为Vi=Vpg.本文在此异向波速模型基础之上，将垂向上的应力波按各岩层波速值大小进行分段处理，提出一种简化的分层速度定位模型SV，以期使微震定位精度得到提升.

3.1 应力波走时关系式推导

如图1所示，假定微震监测区域岩体由四种不同波速的平行岩层组成，自下而上依次编号为①、②、③和④类，对应的层速度值分别表示为V1、V2、V3和V4.实际地震波在不同介质间传播时是遵从费曼原理按折线传播，巩思园等(2012)将矿区地表检波器接收到微震应力波(层面垂向上的应力波)的传播路径近似为直线，并将垂向上应力波波速值视作区别于水平向的均值.本文考虑到垂向应力波路径穿过的各岩层波速值不同这一特征，将对应在各层岩体中的走时由相应的空间距离以及波速值表示出来，然后求和得到应力波总走时.具体地，以3号传感器接收到的在①类波速岩层发生的微震事件应力波为例，推导其走时关系式如下：

通过震源与编号3传感器的空间直线PS可用参数式方程组表达为：

(4)

式中：k为直线参数；(x0，y0，z0)为震源(P)的空间坐标；(x3，y3，z3)为编号3传感器(S)的空间坐标.

由于①类和②类波速岩体交界面、②类和③类波速岩体交界面以及③类和④类波速岩体交界面互相平行，其空间平面一般解析式分别表示为：

(5)

式中：A，B，C是岩体交界面法向向量的三个分量值.D1,2、D2,3、D3,4分别为相应交界面一般式方程中常数项.

经过推导，编号3传感器接收到发生在①类波速岩层中的微震事件应力波走时Δt3：

(6)式中，α3和β3定义为空间距离参数，由(7)式计算得到：

(7)

在实际工程中，为了达到良好的监测效果，监测网络呈网状布置，各传感器位于不同波速的岩层中.这样，同一个微震事件的应力波传播到各个传感器所经过的岩层个数和岩层类别不一样.由前文可以类比得到，某微震事件应力波传播到编号i传感器的走时Δti可以由(8)式表示为：

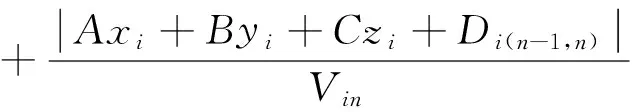
(8)

其中，空间距离参数αi和βi为：

(9)

图1 速度分层岩体中应力波传播特征Fig.1 Propagation characteristics of stress waves in rock mass with stratified velocities

式(8)和(9)中：从震源发出的应力波传播到编号i传感器所经过的波速层依次编号为1，2，…，n；层速度依次为Vi1，Vi2，…，Vin；应力波所穿过不同波速层交界面的数学解析式中常数项依次为Di(1,2)，Di(2,3)，…，Di(n-1,n).

(10)3.2 目标函数建立

基于前文速度分层区域岩体的应力波走时关系，可以构建因变量为到时和因变量为到时差两种形式的分层速度定位目标函数如下：

因变量为到时的分层速度定位目标函数：

(11a)

因变量为到时差的分层速度定位目标函数：

(11b)

上述等式右边含有参数：传感器空间坐标(xi，yi，zi)、分层模型空间几何参数(A，B，C，D)、微震信号初至时刻ti、层速度值Vi、微震震源参数(x0，y0，z0，t0).本文采用因变量为到时差的目标函数(11b).

通过上述推导，可以看出，如果微震震源发生在不同的岩层，那么对应目标函数的具体表达形式也不同.因此，在利用遗传算法求解微震空间坐标的过程中，需要分波速层进行搜索，具体波速层η对应的搜索可行域Ωη按如下线性规划不等式加以限定：

(12)

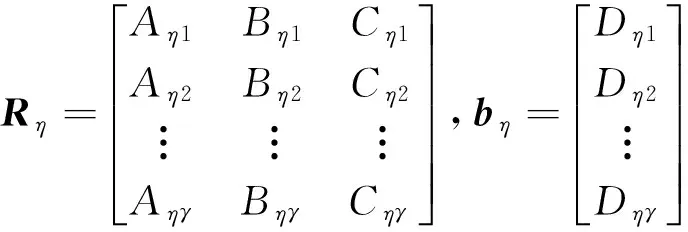
其中：η为波速层编号；Aη，Bη，Cη，Dη为边界面解析式方程参数；γ为边界面个数.

3.3 定位模型构建

在分层速度定位模型中，采用遗传算法进行分层速度定位目标函数最优化求解，属于目标函数最小化问题.但是，在遗传算法中，种群是向适应度值高的方向进化.因此，需要建立目标函数与适应度函数值之间的映射关系.本文采用的适应度函数H与目标函数f的映射关系如下：

(13)

式中：cmax是当前所有或最近k代种群中f的最大值，并且cmax随遗传代数不断变化.图2是目标函数的遗传算法优化流程.在优化求解过程中，当遗传算法达到以下两个条件之一则终止算法：达到最大遗传代数N(条件A)；遗传代种群距离小于阈值Δd(条件B).对每个波速层求解时，如果因达到条件A而终止算法，则认为该波速层的震源优化解不存在；如果因达到条件B而终止，则认为该波速层的解存在，同时如果终止种群的最优个体适应度值和平均适应度值分别大于其阈值H和h，则认为解是可行的.终止种群中的最优个体作为该波速层的震源优化解，同时记录其对应的目标函数值.从解存在的各个波速层中，选取目标函数值最小者对应的震源优化解作为最终定位结果，同时其目标函数值作为误差值来评价该定位结果的可靠性.

图2 遗传算法非线性目标函数优化流程图Fig.2 Flow diagram of the nonlinear objective function optimization using GA

在此基础上，如图3所示，本文构建分层速度定位模型分为三个模块：参数准备、层速度反演、微震定位：

(1) 模块Ⅰ：参数准备.确定监测区域岩体范围，建立坐标系和分层速度几何模型.然后划定波速层，并计算不同波速层交界面解析式方程；确定各岩层遗传算法搜索可行域Ω；根据监测区域岩体范围，优化布置传感器网络，得到传感器坐标；综合计算速度和精度要求，设定遗传算法优化终止参数.

图3 分层速度定位模型流程图Fig.3 Flow chart of stratified velocity location model

(2) 模块Ⅱ：层速度反演.收集现场岩爆或施工爆破事件数据，拾取相应各通道传感器采集到的波形起跳时刻.根据岩爆或者施工爆破事件空间坐标(xb，yb，zb)判断其所在波速层编号为k，由岩爆或者施工爆破事件空间坐标、分层模型边界面解析式参数和传感器坐标，按公式(11b)生成岩层k(波速层k)目标函数并采用遗传算法计算层速度组合优化解，将其用于模块Ⅲ微震定位.

(3) 模块Ⅲ：微震定位.微震系统采集现场微震事件波形信号，拾取波形起跳时刻.由分层模型边界面解析式参数、传感器坐标和模块Ⅱ中求解得到的层速度组合值，按公式(11b)依次生成各岩层(波速层)目标函数并采用遗传算法在可行域Ωη中搜索得到相应微震震源参数优化解(xη0，yη0，zη0)及相应目标函数值fη.在满足解存在条件的各波速层中选取目标函数值最小者对应的微震震源优化解作为最终微震震源参数计算值.

实际工程应用中，微震监测初期阶段，根据地质资料对区域岩体进行岩层划分，并在建议的岩体波速值附近，利用模块Ⅱ进行层速度组合最优化求解.随着对区域岩体的施工开挖和支护开展，岩体质量不断改变、应力不断调整，实际层速度组合也随之改变.为了保证微震源定位精度，在监测期间，应定期对波速层重新划分并进行现场人工爆破试验对速度组合值进行更新计算.

4 工程应用

白鹤滩水电站位于金沙江下游，左岸边坡为顺向坡，倾向河流上游南东方向，倾角较缓；岩体内部发育主要断层F14、F17及多个小断层、层内层间错动带.左岸拱肩槽建基面开挖高程为600～834 m，规模巨大.岩体开挖卸荷必然引起断层及层间、层内错动带高应力区裂隙萌生、发育及扩展，内部微破裂往往是岩质边坡外观变形和失稳破坏的前兆.

图4 左岸边坡传感器阵列布置图Fig.4 Layout of sensor array on slope of left bank

如图4所示，为了实现对坝基边坡及其坡内廊道开挖卸荷过程围岩损伤的实时监测，左岸边坡安装了加拿大ESG微震监测系统，系统由HNAS主机处理系统、Paladin(台站)采集系统、单轴加速度传感器和三维可视化软件四部分组成.其中，HNAS通过网络控制各个台站(Paladin)，设置信号增益、采样频率和触发阈值等参数，从而实现全天候连续采集；Paladin为广泛使用的24位数据模数转换系统；单轴加速度传感器灵敏度为0.7Volts、频率响应范围为50 Hz～5 kHz.白鹤滩左岸边坡安装了3套Paladin采集系统，共18通道单轴加速度传感器阵列分别布置在610 m高程的1#灌排洞及施工连接洞、660 m高程的2#灌排洞和750 m高程的4#灌排洞及抗力体排水洞内.

4.1 左岸边坡分层速度定位模型建立

4.1.1 波速层划分

在实际工程中，按照地层岩石物性将区域岩体分成若干个厚度不等的岩层，各层之间的波速值各不相同，这种波速的分层同地层的地质年代、岩性上的分层基本上是一致的.但地质分层比速度分层细，在通常情况下地质年代不相同但岩性相同的一些地层可以成为一个速度层，这在地震地层学中被称为层序“穿时现象”.

如图5所示，白鹤滩左岸边坡为顺层岩质边坡，各岩层产状近似为N45°E，SE∠20°.开挖过后的坝基拱肩槽岩体岩质坚硬，呈微新状态，无卸荷或弱卸荷.根据坝基勘探资料，其岩体波速分类列于表1中.如图6所示，根据传感器网络布置范围和边坡坡面形状，确定模型尺寸和边界面；结合岩性和岩石类别，将模型区域岩体进行波速分层处理：共分为11层，4种类别，各波速交替出现，相应厚度由地质勘探图纸资料换算得到.

4.1.2 层速度值确定

现场收集到610 m高程灌排廊道的4个开挖爆破数据，采用模块Ⅱ在波速建议值附近用遗传算法搜寻层速度组合最优解，计算结果列于表2中.取由4个爆破事件计算得到的层速度优化值的近似平均值V1=4500 m·s-1，V2=4900 m·s-1，V3=3750 m·s-1，V4=5000 m·s-1作为分层速度定位模型的层速度组合值并用于模块Ⅲ进行微震定位.

4.2 单一速度定位模型和分层速度定位模型对比

本文利用ESG微震监测系统对左岸边坡微震事件进行实时采集，拾取各有效通道信号起跳时刻，然后采用Matlab语言编程来分别实现单一速度已知模型和分层速度定位模型定位.

2015年4月1—18日期间，白鹤滩坝址区边坡坡外部分未进行开挖，工程施工集中在750 m高程置换洞和610 m高程灌排廊道的开挖.边坡层内错动带LS331和LS337受到坡内廊道开挖卸荷扰动，内部微破裂沿其分布带附近萌生和发展，是主要的岩体损伤区.单一速度已知模型采用4个波速区波速的近似均值4600 m·s-1，分层速度模型采用前文所述模型.首先，利用单一速度已知模型对2015年4月1—18日期间微震监测系统采集的微震事件进行定位，圈定层内错动带LS331和LS337附近区域的微震事件；然后，利用分层速度模型对上述圈定事件进行重新定位.图7给出了2015年4月6日18∶59∶55.234″事件的波形图，其中有12个通道监测到了有效的微震波形(DA_001等为通道编号).

表1 岩体波速分类Table 1 Classification of rock mass velocities

图5 左岸边坡拱轴线地质剖面图Fig.5 Geologic cross section along the arch axis at slope of left bank

时间爆破孔底坐标(m)层速度优化值(m·s-1)NEUV1V2V3V42015-04-1815∶253012794.600589164.126613.3434563.164857.443641.865032.972015-04-1903∶023012750.942589220.404607.0454533.674708.463863.044957.352015-04-1904∶233012793.056589166.741612.9794512.954881.003616.945050.292015-04-1913∶013012848.356589028.321617.9494450.425053.863938.784942.95

图6 分层速度定位几何模型Fig.6 Geometric model of SV

单一速度模型和分层速度模型的定位结果以小球的形式分别画在图8a和8b中，其中小球的颜色表示微震事件发生所在的时间段.从图8中定位结果图对比来看，单一速度已知模型定位的微震事件分散在层内错动带LS331和LS337附近，无明显的分布规律；分层速度模型定位的微震事件更接近层内错动带LS331和LS337，并呈条带状分布.通过计算某个微震事件到两个层内错动带的距离，然后选择较小的距离值作为评价该微震事件偏离层内错动带程度大小的指标.该指标值越小，表明微震事件的空间位置越靠近层内错动带；反之，则表明越远离层内错动带.计算结果表明，单一速度模型定位的微震事件中，最大偏离程度指标为32.505 m，最小为1.364 m，平均为9.134 m；分层速度模型定位的微震事件中，最大偏离程度指标为13.923 m，最小为0.866 m，平均为3.895 m.由此可以看出，采用分层速度定位模型，最大、最小和平均偏离程度指标分别降低了57.17%、36.51%和57.35%，这说明白鹤滩分层速度定位模型的微震事件定位结果较单一速度模型更加合理可靠.需要指出的是，精确的速度层划分是提高该算法定位精度的关键.白鹤滩分层速度定位模型中，对层速度组合进行更加精细的划分能够进一步提高定位精度.

图7 2015年4月6日18∶59∶55.234″事件波形Fig.7 Waveforms of an event at 18∶59∶55.234″ on April 6, 2015

5 结论与展望

(1) 本文针对层状区域岩体，在异向波速模型的基础上，对垂向上应力波按波速值大小进行分段区别，推导了分层速度应力波走时关系式，建立了分层定位目标函数，并基于此提出了简化的分层速度定位模型SV.该模型包括参数准备、层速度反演、微震定位三个模块.

(2) 在进行分层速度目标函数优化求解时，采用了具有全局最优、不依赖优化初值和强鲁棒性特点的遗传算法作为最优化工具，使目标函数优化求解过程稳定性和全局最优的要求得到了保证.

(3) 将该速度模型应用到白鹤滩水电站左岸边坡，通过定位效果对比，分层速度定位模型定位微震事件的最大、最小和平均偏离层内错动带程度指标较单一速度模型分别降低了57.17%、36.51%和57.35%.

(4) 本文提出的改进定位模型考虑了因各岩层应力波波速值大小不同而对走时计算的影响，同时能采用遗传算法对建立的目标函数实现稳定求解.相比单一速度模型，定位精度得到了提高.然而，受到岩体应力松弛和风化作用影响，同层岩体各部位波速存在差异，囿于层速度划分无法达到绝对精细，势必在一定程度上影响微震事件的定位精度.为了提高定位精度，后期需要考虑对层内速度进行分区，在寻找能够稳定实现、更加符合应力波实际走时计算的定位模型方面进行改进和完善.

Bai C Y, Greenhalgh S. 2006. 3D local earthquake hypocenter determination with an irregular shortest-path method.BulletinoftheSeismologicalSocietyofAmerica, 96(6): 2257-2268.

Bai C Y, Zhao R, Greenhalgh S. 2010. Rapid 3-D earthquake location using a hybrid global-local inversion approach.PureandAppliedGeophysics, 167(11): 1377-1387.

Chen B R, Feng X T, Li S L, et al. 2009. Microseism source location with hierarchical strategy based on particle swarm optimization.ChineseJournalofRockMechanicsandEngineering(in Chinese), 28(4): 740-749.Collins D S, Pinnock I, Toya Y, et al. 2014. Seismic event location and source mechanism accounting for complex block geology and voids.∥ 48th US Rock Mechanics/Geomechanics Symposium. Minneapolis, Minnesota: American Rock Mechanics Association. Dong L J, Li X B, Tang L Z, et al. 2011. Mathematical functions and parameters for microseismic source location without pre-measuring speed.ChineseJournalofRockMechanicsandEngineering(in Chinese), 30(10): 2057-2067.

Feng G L, Feng X T, Chen B R, et al. 2015. Sectional velocity model for microseismic source location in tunnels.TunnellingandUndergroundSpaceTechnology, 45: 73-83.

Gao Y T, Wu Q L, Wu S C, et al. 2015. Source parameters inversion based on minimum error principle.JournalofCentralSouthUniversity(ScienceandTechnology) (in Chinese), 46(8): 3054-3060.Gong S Y, Dou L M, Ma X P, et al. 2012. Study on the construction and solution technique of anisotropic velocity model in the location of coal mine tremor.ChineseJournalofGeophysics(in Chinese), 55(5): 1757-1763, doi: 10.6038/j.issn.0001-5733.2012.05.033.Hosseini Z, Collins D, Shumila V, et al. 2015. Induced Microseismic Monitoring in Salt Caverns.∥ 49th US Rock Mechanics/Geomechanics Symposium. San Francisco, California: American Rock Mechanics Association. Inglada V. 1928. The calculation of the stove coordinates of a Nahbebens.GerlandsBeitrageZurGeophysik, (19): 73-98.

Jiang F X, Yang S H, Cheng Y H, et al. 2006. A study on microseismic monitoring of rock burst in coal mine.ChineseJournalofGeophysics(in Chinese), 49(5): 1511-1516.

Kaiser J. 1950. Studies on the occurrence of noise in the tensile test [Ph. D. thesis]. Munich: Technical University of Munich.

Leighton F, Blake W. 1970. Rock noise source location techniques. Washington: Bureau of Mines.

Li J, Gao Y T, Xie Y L, et al. 2014. Improvement of microseism locating based on simplex method without velocity measuring.ChineseJournalofRockMechanicsandEngineering(in Chinese), 33(7): 1336-1345.

Liu F Y. 1984. Simultaneous inversion of earthquake hypocenters and velocity structure (Ⅰ)——theory and method.ChineseJ.Geophys. (ActaGeophysicaSinica) (in Chinese), 27(2): 167-175.

Liu J, Zheng S H, Wong Y L. 2003. The inversion of non-elasticity coefficient, source parameters, site response using genetic algorithms.ActaSeismologicaSinica(in Chinese), 25(2): 211-218.

Lian C, Li S L, Dong M, et al. 2006. Method of spherical surface shearing in earthquake location.JournalofGeodesyandGeodynamics(in Chinese), 26(2): 99-103.

Lu C P, Dou L M, Wang Y F, et al. 2010. Microseismic effect of coal materials rockburst failure induced by hard roof.ChineseJ.Geophys. (in Chinese), 53(2): 450-456, doi: 10.3969/j.issn.0001-5733.2010.02.024.

Obert L. 1977. The microseismic method: discovery and early history.∥Proceedings of the First Conference on Acoustic Emission/Microseismic Activity in Geologic Structures and Materials. Clausthal-Zellerfeld: Trans. Tech. Publications, 11-12. Pavlis G L, Booker J R. 1980. The mixed discrete-continuous inverse problem: Application to the simultaneous determination of earthquake hypocenters and velocity structure.JournalofGeophysicalResearch:SolidEarth, 85(B9): 4801-4810. Song W Q, Xu B B, Yu Z C, et al. 2015. Reconstruction of the micro-seismic source vector field and fissure interpretation based on the anisotropy analysis.ChineseJ.Geophys. (in Chinese), 58(2): 656-663, doi: 10.6038/cjg20150226.Spencer C, Gubbins D. 1980. Travel-time inversion for simultaneous earthquake location and velocity structure determination in laterally varying media.GeophysicalJournalInternational, 63(1): 95-116. Spence W. 1980. Relative epicenter determination using P-wave arrival-time differences.BulletinoftheSeismologicalSocietyofAmerica, 70(1): 171-183.

Thurber C H. 1985. Nonlinear earthquake location: theory and examples.BulletinoftheSeismologicalSocietyofAmerica, 75(3): 779-790.

Wang H T, Chen Y, Zhuang C T. 2006. A local earthquake locating method based on genetic algorithm.Earthquake(in Chinese), 26(2): 12-18.

Xu N W, Tang C A, Li L C, et al. 2011. Microseismic monitoring

and stability analysis of the left bank slope in Jinping first stage hydropower station in southwestern China.InternationalJournalofRockMechanicsandMiningSciences, 48(6): 950-963.

Zhang B H, Deng J H, Zhou Z H, et al. 2012. Analysis of monitoring microseism in areas controlled by faults near powerhouse in Dagangshan hydropower station.RockandSoilMechanics(in Chinese), 33(Suppl. 2): 213-218.

Zhang H, Zhang Z L, Yao H, et al. 2014. The study on precise positioning of earthquake in Dachang mining area based on genetic algorithm.ChineseJournalofEngineeringGeophysics(in Chinese), 11(2): 260-265.

Zhao Z, Zeng R S. 1987. A method for improving the determination of earthquake hypocenters.ChineseJ.Geophys. (in Chinese), 30(4): 379-388.

附中文参考文献

陈炳瑞, 冯夏庭, 李庶林等. 2009. 基于粒子群算法的岩体微震源分层定位方法. 岩石力学与工程学报, 28(4): 740-749.

董陇军, 李夕兵, 唐礼忠等. 2011. 无需预先测速的微震震源定位的数学形式及震源参数确定. 岩石力学与工程学报, 30(10): 2057-2067.

高永涛, 吴庆良, 吴顺川等. 2015. 基于误差最小原理的微震震源参数反演. 中南大学学报, 46(8): 3054-3060.

巩思园, 窦林名, 马小平等. 2012. 煤矿矿震定位中异向波速模型的构建与求解. 地球物理学报, 55(5): 1757-1763, doi: 10.6038/j.issn.0001-5733.2012.05.033.

姜福兴, 杨淑华, 成云海等. 2006. 煤矿冲击地压的微地震监测研究. 地球物理学报, 49(5): 1511-1516.

李健, 高永涛, 谢玉玲等. 2014. 基于无需测速的单纯形法微地震定位改进研究. 岩石力学与工程学报, 33(7): 1336-1345.

刘福田. 1984. 震源位置和速度结构的联合反演(Ⅰ)——理论和方法. 地球物理学报, 27(2): 167-175.

刘杰, 郑斯华, 黄玉龙. 2003. 利用遗传算法反演非弹性衰减系数、震源参数和场地响应. 地震学报, 25(2): 211-218.

廉超, 李胜乐, 董曼等. 2006. 球面交切法地震定位. 大地测量与地球动力学, 26(2): 99-103.

陆菜平, 窦林名, 王耀峰等. 2010. 坚硬顶板诱发煤体冲击破坏的微震效应. 地球物理学报, 53(2): 450-456, doi: 10.3969/j.issn.0001-5733.2010.02.024.

宋维琪, 徐奔奔, 喻志超等. 2015. 基于各向异性分析的微地震震源矢量场重建和裂缝解释. 地球物理学报, 58(2): 656-663, doi: 10.6038/cjg20150226.

王洪体, 陈阳, 庄灿涛. 2006. 基于浮点遗传算法的近震定位方法. 地震, 26(2): 12-18.

张伯虎, 邓建辉, 周志辉等. 2012. 大岗山水电站厂房断层控制区域微震监测分析. 岩土力学, 33(增2): 213-218.

张华, 张忠利, 姚宏等. 2014. 基于遗传算法的大厂矿区地震定位研究. 工程地球物理学报, 11(2): 260-265.

赵珠, 曾融生. 1987. 一种修定震源参数的方法. 地球物理学报, 30(4): 379-388.

(本文编辑 何燕)

Improvement of microseismic location based on an anisotropic velocity model

DAI Feng1， GUO Liang1， XU Nu-Wen1,2*， FAN Yi-Lin3， XU Jian3， JIANG Peng1

1StateKeyLaboratoryofHydraulicsandMountainRiverEngineering,SichuanUniversity,Chengdu610065，China2SchoolofCivilandHydraulicsEngineering,ShandongUniversity,Ji′nan250061,China3ChinaThreeGorgesCorporation，Beijing100038，China

As a kind of three-dimensional detection of seismic events, microseismic (MS) monitoring techniques have been widely used in the world for many years to assess the stability of surrounding rock. The location of MS events is foundation of MS monitoring. Resulting from anisotropy and inhomogeneity of regional rock masses, the velocity of stress waves may be different in different directions and areas. So, it is difficult to figure out a reasonably accurate location. Aimed at the regional rock masses with stratified velocities, a simplified and stable stratified velocity location model (SV) is proposed.

Microseismic monitoring; Anisotropic velocity model; Stratified velocity location model (SV); Genetic algorithm (GA); Rock slope

10.6038/cjg20160914.Dai F， Guo L， Xu N W, et al. 2016. Improvement of microseismic location based on an anisotropic velocity model.ChineseJ.Geophys. (in Chinese),59(9):3291-3301,doi:10.6038/cjg20160914.

国家重点基础研究发展计划(973计划)项目(2015CB057903)；国家自然科学基金项目(51374149，51679158)资助.

戴峰，男，1978年生，博士，教授，2010年博士毕业于加拿大多伦多大学土木工程系，主要从事岩石动力学与工程研究.

*通讯作者 徐奴文，男，1981年生，博士，副研究员，2005年毕业于武汉科技大学土木工程系，主要从事岩土工程灾害机理与微震监测方面的研究. E-mail：xunuwen@scu.edu.cn

10.6038/cjg20160914

P315

2015-10-09，2016-01-28收修定稿

戴峰， 郭亮， 徐奴文等. 2016. 基于异向波速模型的微震定位改进. 地球物理学报，59(9):3291-3301,