LU分解的基本计算原理算法实现
2016-11-16南京林业大学理学院信息与计算科学系
南京林业大学理学院信息与计算科学系 刘 煜
LU分解的基本计算原理算法实现
南京林业大学理学院信息与计算科学系 刘 煜
一、方法、算法与程序设计
1.方法:
首先将系数矩阵进行LU分解,若题目要求求解线性方程,则通过以下两步骤来达到目的:
(1)由LY=B解出Y;
(2)由UX=Y解出X;
解出以上两个方程即可。
2.算法:
①LU分解步骤:
步骤一:输入系数矩阵A;
步骤二:LU分解:
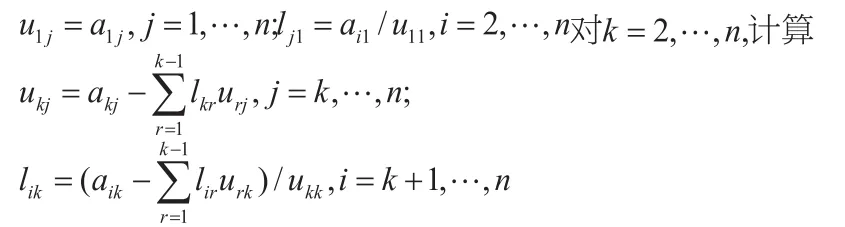
②直接三角分解法算法:
步骤一、步骤二同LU分解。
步骤三:用向前消去法解下三角方程组LY=b


3.程序设计:
①LU分解:
Matlab:
fuction [L,U,flag]=LU_Decom(A)
[n,m]=size(A);
if n~=m
error(’The rows and columns of matrix A must be equal!’);
return;
end
L=eye(n);
U=zeros(n);
flag=’0K’;
for k=1:n
for j=k:n
z=0;
for q=1:k-1
z=z+L(k,q)*U(q,j);
end
U(k,j)=A(k,j)-z;
end
if abs(U(k,k))<eps
flag=’failure’;return;
end
for i=k+1:n
z=0;
for q=1:k-1
z=z+L(i,q)*U(q,k);
end
L(i,k)=(A(i,k)-z)/U(k,k);
end
end
②直接三角形法:
Matlab:
function [x,l,u]=malu(A,b)
n=length(b);u=zeros(n,n);
Study on the variation law of pollutant mixing zone in the bend river
l=eye(n,n);u(1,:)=A(1,:);
l(2:n,1)=A(2:n,1)/u(1,1);
for k=2:n
u(k,k:n)=A(k,k:n)-l(k,1:k-1)*u(1:k-1,k:n);
l(k+1:n,k)=(A(k+1:n,k)-l(k+1:n,1:k-1)*u(l:k-1,k))/u(k,k);
end
y=zeros(n,1);
y(1)=b(1);
y(k)=b(k)-l(k,1:k-1)*y(1:k-1);
end
x=zeros(n,1);
x(n)=y(n)/u(n,n);
for k=n-1:-1:1
x(k)=(y(k)-u(k,k+1:n)*x(k+1:n))/u(k,k);
end
二、实例
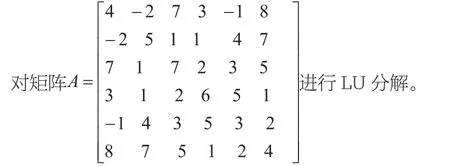
解:调用LU_Decom(A)函数。
在MATLAB命令窗口执行。
>> A=[4 -2 7 3 -1 8;-2 5 1 1 4 7;7 1 7 2 3 5;3 1 2 6 5 1;-1 4 3 5 3 2;8 7 5 1 2 4]
>> [L,U,flag]=LU_Decom(A)
得到以下计算结果:


