螺旋桨叶片定时截尾疲劳试验评估方法研究
2016-11-16牛宏伟
牛宏伟
(中国飞行试验研究院,陕西西安710089)
螺旋桨叶片定时截尾疲劳试验评估方法研究
牛宏伟
(中国飞行试验研究院,陕西西安710089)
研究了螺旋桨叶片疲劳试验中定时截尾数据的处理和评估方法。采用线性Goodman修正和Miner损伤累积法则将截尾疲劳寿命转换为疲劳极限样本数据,对该样本建立似然方程,利用似然方程组的极值条件迭代求解疲劳极限的最大似然估计量,并通过Monte-Carlo假设验证了方法的准确性。根据疲劳极限的最大似然估计可以得到更准确的S-N曲线,从而更有效地进行疲劳寿命评估。
螺旋桨叶片 疲劳极限 截尾数据 Monte Carlo检验 S-N曲线
0 引言
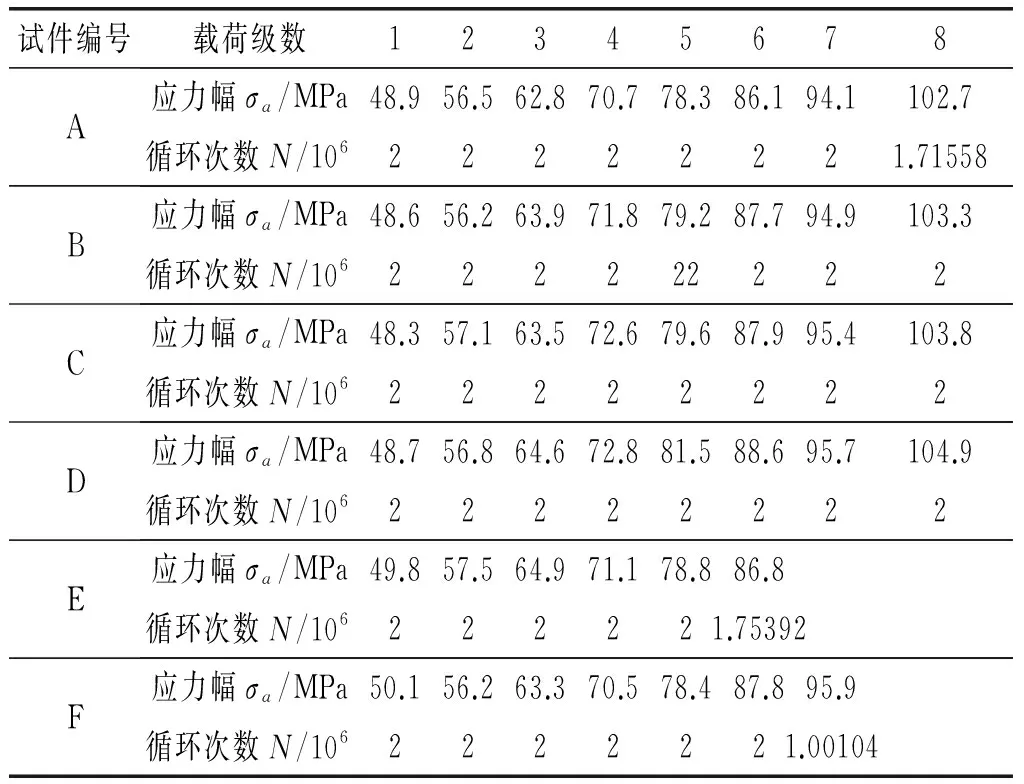
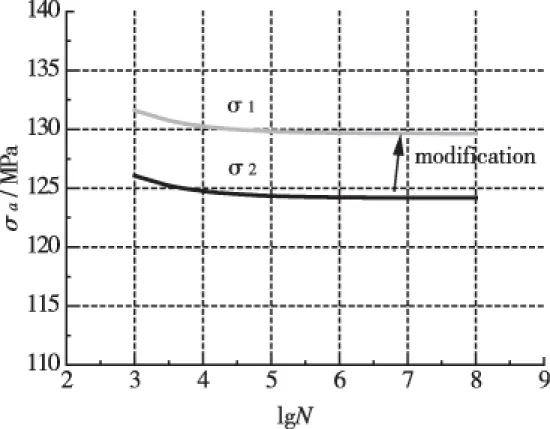
在金属结构疲劳试验中,经常会受时间和成本限制,当总加载时间或循环数达到某一特定值时,即中止试验。例如从总样本中随机抽取n个试件进行疲劳试验,当达到事先制定的循环次数N0就结束试验,这时只有r(r 本文以某螺旋桨叶片的高周疲劳试验为研究对象。取6件全尺寸试件进行疲劳试验,采用分级步进加载,平均应力为控制在74±1 MPa,应力幅增量控制在±7.84 MPa左右。若总循环次数达到1.6×107时,试件还未破坏,则停止试验,应力幅及试件的循环次数见表1。 表1 疲劳试验应力幅与循环次数 研究表明,金属材料的疲劳寿命在长寿命区遵循三参数威布尔分布[9-10],而疲劳极限符合对数正态分布[11-12]。由于每级载荷都不同,以寿命作为统计指标没有明确意义,需以疲劳强度作为指标。描述高周疲劳S-N曲线的Stromeyer方程为: (1) 其中A和α为形状参数,根据参考文献[9],A=0.482 8,α=0.5。利用线性Goodman修正将循环载荷换算到R=-1的应力幅: (2) 其中σb为试件材料的拉伸极限,σ-1为对称疲劳极限。每级载荷的理论寿命为: 图1 疲劳极限求解迭代程序流程图 (3) (4) 其中Q为总载荷级数。根据上述方程组编程迭代求解,在迭代中要不断剔除不构成损伤的载荷级,程序流程见图1。 求解结果见表2,按是否为完全数据对试件进行重新编号,1~r为完全寿命件,r+1~n为截尾寿命件,对应关系为A→1,E→2,F→3,B→4,C→5,D→6。 表2 疲劳极限截尾数据 经统计表明叶片疲劳极限符合对数正态分布,即σ∞i~LN(μ,σ2),或令x=ln(σ∞i),即得到对数疲劳极限的样本空间: x={4.851 9,4.685 0,4.786 6,4.858 4,4.861 9,4.872 8} (5) 在疲劳试验中应得到的完全寿命结果的概率为[13-14]: =f(i=1~r) (6) (7) 似然函数为: (8) 取对数为: (9) 令ti=(xi-μ)/σ,将x变换为标准正态分布t,代入式(9),按似然函数极大值必要条件,可建立求解母体参数最大似然估计量公式: (10) (11) (12) (13) 采用期望最大化算法(Expectation Maximization Algorithm)求解方程组(10)(11),其思路是在期望与方差之间反复迭代,直至收敛,迭代式为: (14) (15) 图2 迭代收敛曲线 ln(σ∞)~N(4.864 7,0.113 3) (16) (17) (18) 其中AL为给定的精度等级。分别考察精度为0.5%、1%和2%的置信度,见表3。可见无论是小样本还是大样本,在2%精度等级下,估计的置信度达到0.999,在1%等级,置信度也高于0.92,说明本文的最大似然估计是一种无偏估计方法,结果可靠。 表3 估计结果精度及置信度 进行最大似然估计的最终目的准确求解疲劳极限,绘制S-N曲线。通过上文无偏估计得到的疲劳极限为: (19) 若不对截尾进行处理,直接对表2中所有试件疲劳极限求均值,得到的疲劳极限为: (20) 式(1)两边同取对数,求得应力比R=-1的S-N曲线方程分别为:lg(σa-129.632 0)=1.796 5-0.5lg(N)(σ∞=σ1) (21)lg(σa-124.160 0)=1.777 7-0.5lg(N)(σ∞=σ2) (22) 图3 修正前后S-N曲线对比 两种S-N曲线对比见图3。若直接以截尾疲劳极限σ2作为叶片的真实疲劳极限,将忽略未破坏试件剩余的那部分寿命,导致疲劳极限过于保守。而经过最大似然估计的疲劳极限σ1能够真实反映叶片的高周疲劳性能,经过估计修正,疲劳极限有所提高,S-N曲线向上方移动。 本文研究了螺旋桨叶片定时截尾疲劳试验的结果评估方法。首先依据线性Goodman修正和Miner损伤累计法则计算截尾疲劳极限,根据疲劳极限符合对数正态分布的特性,对截尾数据样本进行了最大似然估计,得到母体均值和标准差的估计量。通过Monte Carlo模拟检验,表明该估计结果的精度可达2%以上。该方法可用于准确获取疲劳极限和S-N曲线,以表征叶片的真实疲劳性能。 [1] Yu K, Wang B. Nonlinear combinations of order statistics as efficient alternatives to maximum likelihood estimates for lifetime data analysis[C]//The Third IMS-China International Conference on Statistics and Probability. 2011. [2] Borgan φ. The statistical analysis of failure time data[J]. Journal of the American Statistical Association,2003, 98(464):1084-1085. [3] Ye E H. Consistency of MLE of the parameter of exponential lifetime distribution for random censoring model with incomplete information[J]. Applied Mathematics-A Journal of Chinese Universities, 1995, 10(4):379-386. [4] 李海波,张正平,胡彦平,郑德强.基于随机截尾数据下Weibull分布的参数极大似然估计与应用[J].强度与环境,2009,36(4):60-64. [5] Lawless J F. Statistical Models and Methods for Lifetime Data[M]. New York: John Wiley & Sons Inc., 1982. [6] Meeker W Q, Escobar L A. Statistical Methods for Reliability Data [M]. New York: John Wiley & Sons Inc., 1998. [7] Wang W D. New study on MLE for censored lifetime data[C]//Proceedings of Annual Reliability and Maintainability Symposium. Virginia: RAMS, 2005: 308-312. [8] 陈家鼎.随机截尾情况下Weibull分布参数的最大似然估计的相合性[J].应用概率统计,1989,5(3):226-233. [9] 穆志韬, 曾本银. 直升机结构疲劳[M]. 北京:国防工业出版社, 2009. [10] 马群,佟晓君.不完全寿命威布尔分布三参数最大似然估计式求解[J].河北理工学院学报,2001,23(2):17-20. [11] 高镇同. 疲劳应用统计学[M].北京:国防工业出版社,1986. [12] 卢小艳,陆山.基于对数正态分布第k试验寿命的分散系数法[J].航空动力学报,2006,21(4):738-740. [13] 王蓉华, 徐晓岭, 费鹤良.对数正态分布参数的近似极大似然估计[J].上海师范大学学报(自然科学版),2000,29(1):39-43. [14] 陈家鼎, 李东风.随机截尾情形下正态分布参数的最大似然估计[J]. 应用数学学报, 2011,34(6):961-975. [15] 刘飞,陈文华,钱萍,杨帆,胡昭光.导弹折叠展开机构工作可靠性的Monte Carlo模拟计算方法研究[J].工程设计学报,2012,19(1):16-19. The estimation method of fixed time censoring fatigue test for aircraft propeller blade NIU Hongwei The processing and estimation method of fixed time censoring data in a propeller fatigue test was investigated. The fatigue limit was derived from fatigue test results by linear Goodman modification and Miner damage accumulation rule. The likelihood equations of this sample were established and solved using E-M iteration algorithm, so as to obtain the maximum likelihood estimation. The algorithm was verified employing Monte Carlo inspection. With the maximum likelihood estimation of the fatigue limit, a more accurate S-N curve was obtained for life assessment of the blade. aircraft propeller blade, fatigue limit, censored data, Monte Carlo inspection, S-N curve V216.3 A 1002-6886(2016)05-0031-04 牛宏伟(1989-),男,陕西省商洛市人,工程师,主要研究方向为航空动力装置飞行试验研究。 2016-03-181 疲劳试验结果

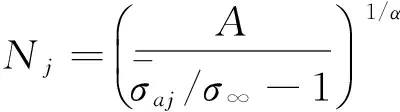


2 疲劳极限的最大似然估计

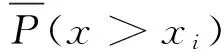
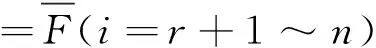

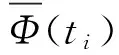
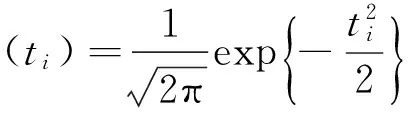
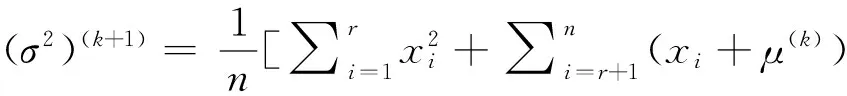

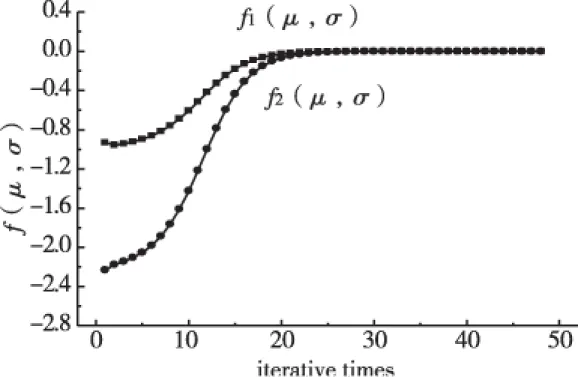
3 Monte Carlo模拟检验

4 S-N曲线求解
5 结论
