NiTi合金动态断裂过程的实验和数值方法研究

韩悌信，曾祥国，郭　杨，杨　鑫，陈华燕，李　洋

（四川大学建筑与环境学院，四川 成都 610065）

NiTi合金动态断裂过程的实验和数值方法研究

韩悌信，曾祥国，郭杨，杨鑫，陈华燕，李洋

（四川大学建筑与环境学院，四川 成都 610065）

为获得NiTi合金的动态起裂韧度和动态扩展速度与动态加载率之间的定量变化规律。利用分离式霍普金森压杆（SHPB）测试系统对单边三点弯曲试样（SENB）进行冲击加载试验，采用实验-有限元相结合的方法，获得动态断裂参数随时间的变化规律。SENB试样裂纹起裂时刻和裂纹扩展速度由粘贴在裂纹尖端的裂纹扩展计（CPG）测定。采用上述方法和数据获得NiTi合金的I型动态起裂韧度和动态扩展速度。实验结果表明：裂纹扩展计测得的起裂时刻与粘贴在同一试样上的监裂应变片测得的结果基本相符，因此可以利用裂纹扩展计代替传统的监裂应变片来监测裂纹起裂时刻，并获得NiTi合金的起裂韧度。同时，可以利用裂纹扩展计（CPG）获得裂纹动态扩展过程，绘制出裂纹扩展速度与时间的关系曲线，从而探讨NiTi合金的动态断裂韧度和裂纹扩展速度与动态加载率之间的定量变化规律。

霍普金森杆；数值方法；NiTi合金；裂纹扩展计；动态断裂过程

0　引　言

NiTi形状记忆合金以其独特的超弹性、形状记忆性能及良好的生物相容性而备受关注，目前已广泛应用于医疗外科、薄膜、航空和微机电等领域［1］。由于形状记忆合金在工程领域的特殊性，其工作环境较为恶劣，常遭受碰撞、挤压等动态荷载。尤其在航空航天领域，形状记忆合金构件一旦破坏，轻则造成巨大的财产损失，重则给宇航员、飞行员的生命造成威胁。结构件的破坏往往是从微小裂纹开始，不断扩展，最后致使构件断裂失效。金属动态断裂韧度包括动态起裂韧度和动态扩展韧度，是分别表征金属抵抗裂纹动态起裂和扩展的基本力学参数，因此，研究其测试方法具有十分重要的意义。

近年来，准静态加载下的断裂韧度测试技术已经比较成熟，并且建立了一系列的国际标准，而霍普金森杆加载的动态断裂实验尚未建立统一的实验标准。正因如此，国内外很多学者都致力于材料动态断裂韧度测试技术的研究。如Tanaka等［2］首先采用双杆加载的动态弯曲实验，运用一维应力波理论计算得到加载于弯曲试样上的入射波和反射波。然而Tanaka只给出了加载力的历史，并未计算应力强度因子。J.R.Berger等［3］采用应变片法对2.25Cr-1Mo钢进行了动态断裂分析，并根据静止裂纹的裂尖应变场确定了应力强度因子时程曲线。李玉龙等［4］基于SHPB系统，用弹簧质量模型求解了三点弯曲试样的动态应力强度因子。张晓欣等［5］结合SHPB测试系统和自编的ANSYS宏程序得到了某船用钢的动态断裂韧度值。杨井瑞等［6］用SCDC试样及裂纹扩展计在SHPB平台上进行实验，采用实验-数值-解析法得到了砂岩的动态断裂韧度和裂纹扩展速度。陈华燕等［7］利用实验和数值结合的方法测量了镁合金AZ91的动态断裂韧性。在微介观断裂方面，Xu等［8］采用混合跨尺度方法研究了微介观尺度下BCC-Fe的裂纹扩展过程。Pei等［9］研究了多晶镍在拉伸载荷下延性-脆性-断裂的转变过程。但尚未见关于测定NiTi合金动态裂纹扩展速度的报道，也未见有结合实验-数值模拟的方法对NiTi合金的动态断裂韧度进行研究。

本文对NiTi合金的单边裂纹三点弯曲试样（SENB）进行SHPB加载，采用自编的ANSYS-APDL命令流对实验过程进行数值模拟，得到动态J积分响应曲线。使用裂纹扩展计（CPG）测量试样的起裂时刻和扩展速度，从而确定不同加载率下的动态断裂韧度和裂纹扩展速度。并将普通应变片（SG）监测到的起裂时间与CPG得到的结果进行对比，验证CPG监测结果的可靠性。

1　实验过程

1.1试样准备

实验所用材料为NiTi合金，其化学成分如表1所示。图1（a）和图1（b）分别为单边裂纹三点弯曲（SENB）试样的几何构型图以及加载状态的实物图。试样长L=100 mm，宽W=20 mm，厚B=10 mm，跨距S=80mm，预置裂纹长度a=10mm。Pi（t）为入射杆对SENB试样的作用力。

表1　Ni55.72at.%-Ti合金板材化学成分

1.2SHPB加载装置

动态实验在 Hopkinson拉/压杆（SHPB）实验平台（KD205-4型）上完成，其加载装置如图2所示。SHPB子弹及入射杆材料为42CrMo钢，弹性模量E=210 GPa，泊松比ν=0.3，密度ρ=7 850 kg/m3。子弹长200mm，入射杆长2000mm，直径均为20mm。入射杆上的SG到整形器-入射杆接触端的距离为1000mm。

1.3裂纹扩展计及其使用

本文采用的CPG如图3所示。CPG由基底和敏感栅组成，其中敏感栅由10根等长但不等宽的卡玛铜薄片并联而成，初始总电阻约为2Ω。CPG的敏感栅总长度l=10mm，宽度h=5mm，相邻两根栅丝的间距l0=1.11mm。在SENB上粘贴CPG时，使CPG的敏感栅丝垂直于裂纹扩展方向（x方向），并将最宽的裂纹栅丝（其电阻为R1）贴近裂纹尖端。

CPG的电路如图4所示。采用型号为APS3003D的恒压源提供3 V的电压。裂纹扩展计与电阻R2=60Ω（本文实测值为59.5Ω）并联，再与保护电阻R1=20 Ω（本文实测值为22.1 Ω）串联，裂纹扩展计的初始电阻为RCPG=2Ω（本文实测值为1.8Ω）。示波器用于记录裂纹扩展计两端的电压。

实验时，随着裂纹的扩展，裂纹扩展计敏感栅丝会随之发生断裂，其阻值会变为RCPG+ΔRCPG，从而引起裂纹扩展计两端电压的变化。由于裂纹扩展计敏感栅丝是逐根断裂的，因此示波器记录的电压信号应该呈现阶梯状突变，而敏感栅丝之间的距离是已知的，这样就可以得到裂纹的扩展速度。

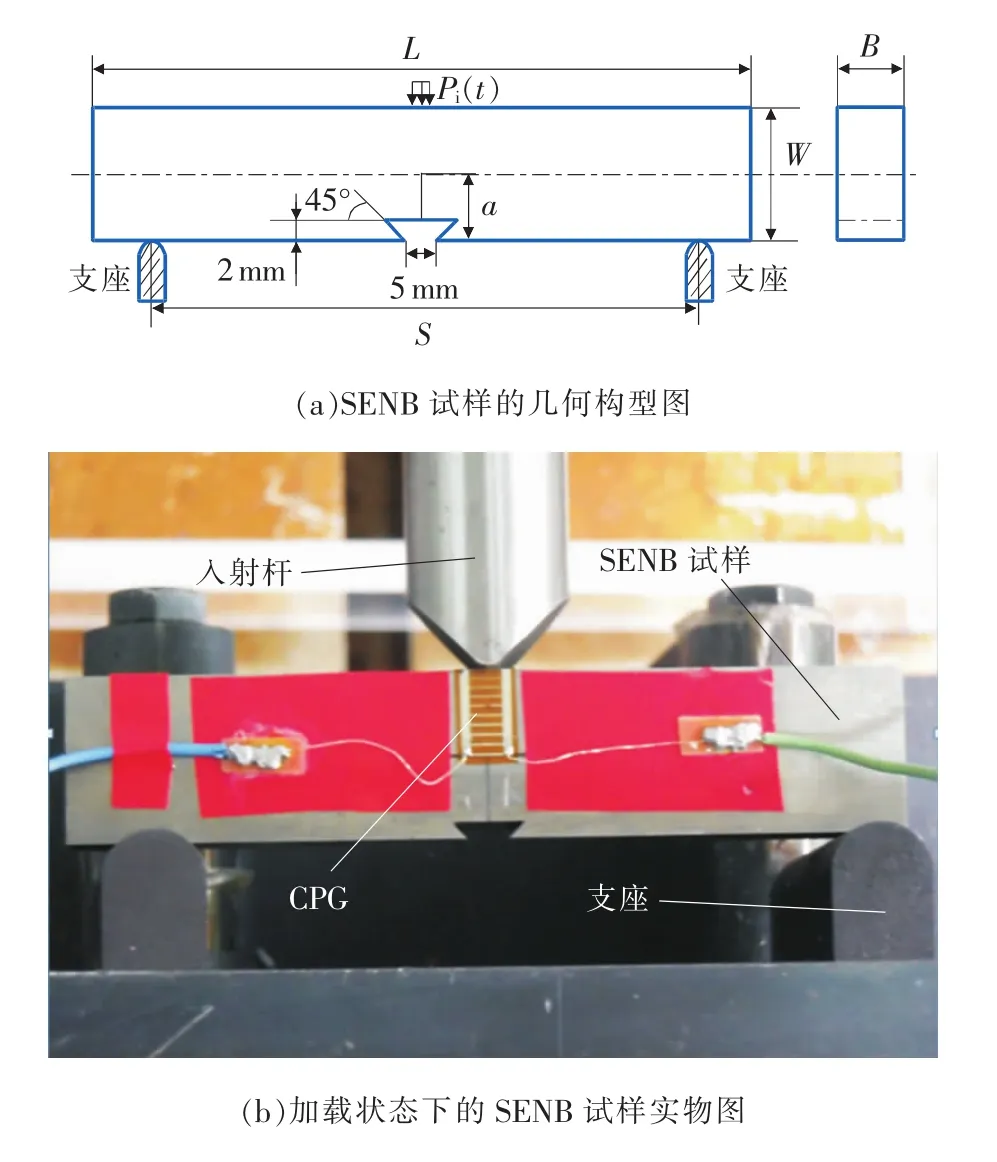
图1　SENB试样几何构型图及实物图

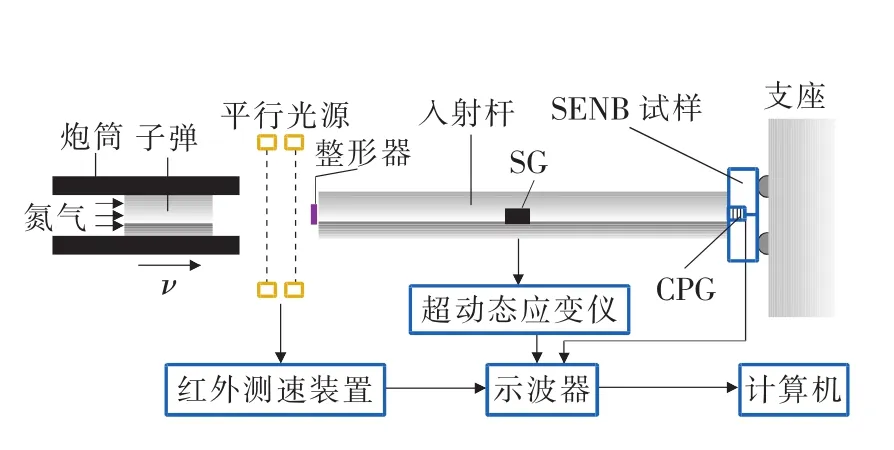
图2　SHPB加载装置图

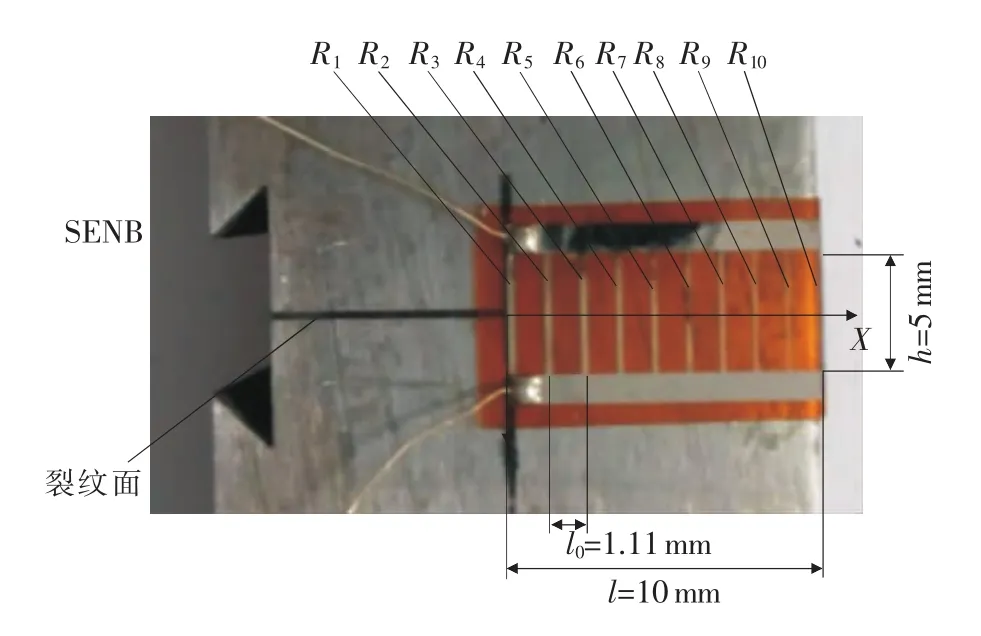
图3　BKX5-4CY型CPG

图4　CPG电路图

2　实验数据处理

2.1动载荷的确定

如图5所示为SENB-01试样（具体参数见表2）加载时示波器上记录的原始电压信号，包括入射杆上SG测得的信号和CPG测得的信号。

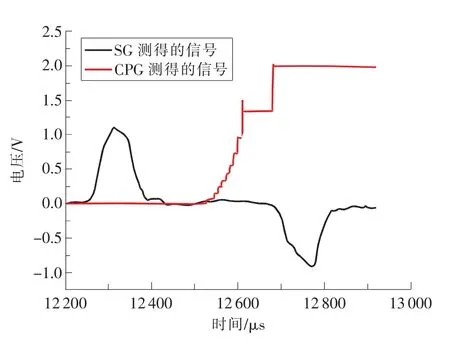
图5　SENB-01试样由SG和CPG测得的原始电压信号

根据电桥工作原理，可得应变片的测量值ε（t）与电压信号ΔU（t）之间的关系：

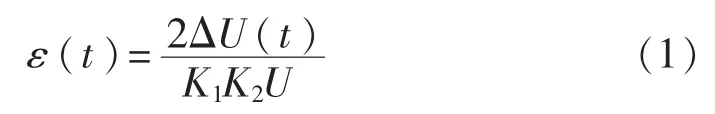
式中：U——电桥的桥路电压，8V；

K1——SG的灵敏系数，1.97；

K2——超动态应变仪的放大系数，100。

则可由图5中入射杆上的电压信号及式（1）计算得到入射杆上的入射波εi（t）和反射波εr（t），如图6所示。

根据一维弹性应力波假设，由入射波、反射波叠加可以得到入射杆对试样的作用力Pi（t）：

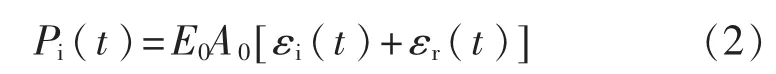
式中，E0、A0分别为入射杆的弹性模量及横截面积。

在试验中，实测记录到的波形的基准线由于受外界的干扰而偏离零线且有震荡，所以，必须对记录到的波形进行整理，以准确地确定波形的起跳点。本文采用文献［10］中提到的方法进行波形处理及确定起跳点。

由图6中入射杆上入射波εi（t）和反射波εr（t）及式（2）计算可得SENB-01试样加载端的动载荷时程曲线，如图7所示。在动态实验中，只关心试样受到载荷以后的响应，因此定义加载波到达试样时刻t0为零时刻，下文中出现的新的时间坐标轴，其原点对应的时刻均为t0（对SENB-01试样，t0=12471.9s）。

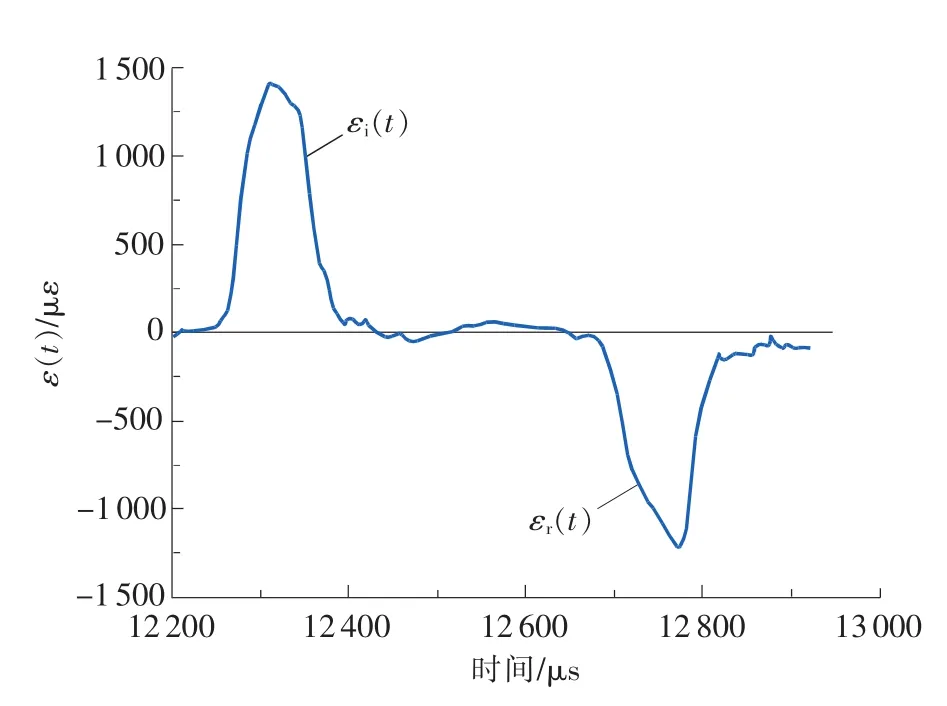
图6　SENB-01试样入射杆上的应变信号

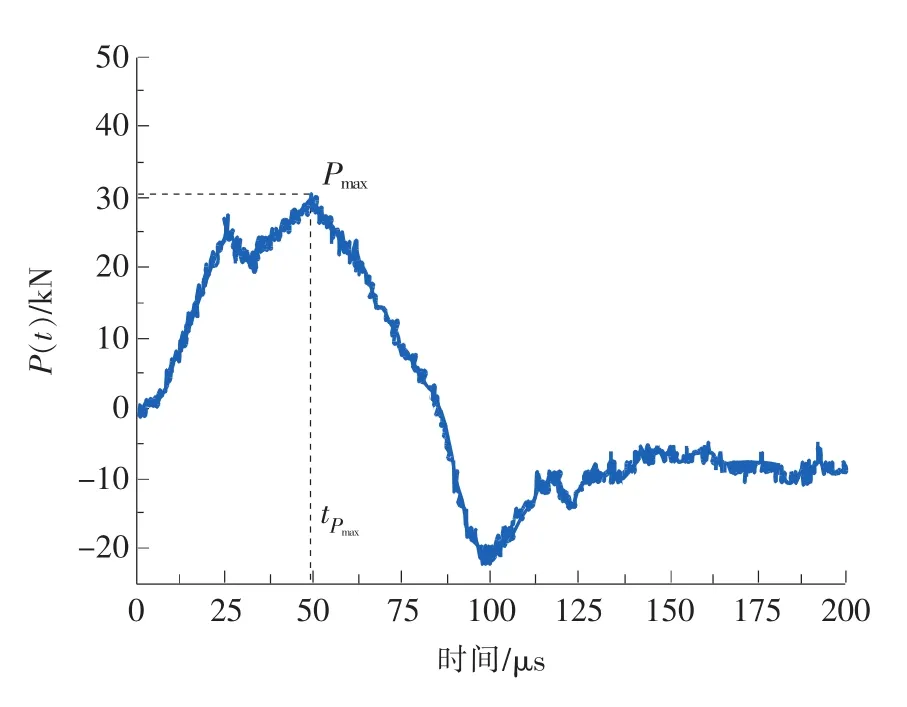
图7　SENB-01试样加载端的动载荷时程曲线

2.2裂纹起裂时刻和扩展速度的测定

如图8所示为SENB-01试样的CPG电压信号及电压对时间的导数。从图中可以看出，随着裂纹的扩展，电压呈阶梯状上升，10个台阶的突变时刻对应CPG上10根敏感栅丝的断裂时刻。根据电压对时间的导数峰值所对应的时刻可以准确地确定CPG上10根敏感栅丝的断裂时刻t1～t10以及相邻2根敏感栅丝断裂的时间差Δt1～Δt9。由于CPG的第1根敏感栅丝是紧贴裂纹尖端的，因此，可以认为起裂时间tf=t1。

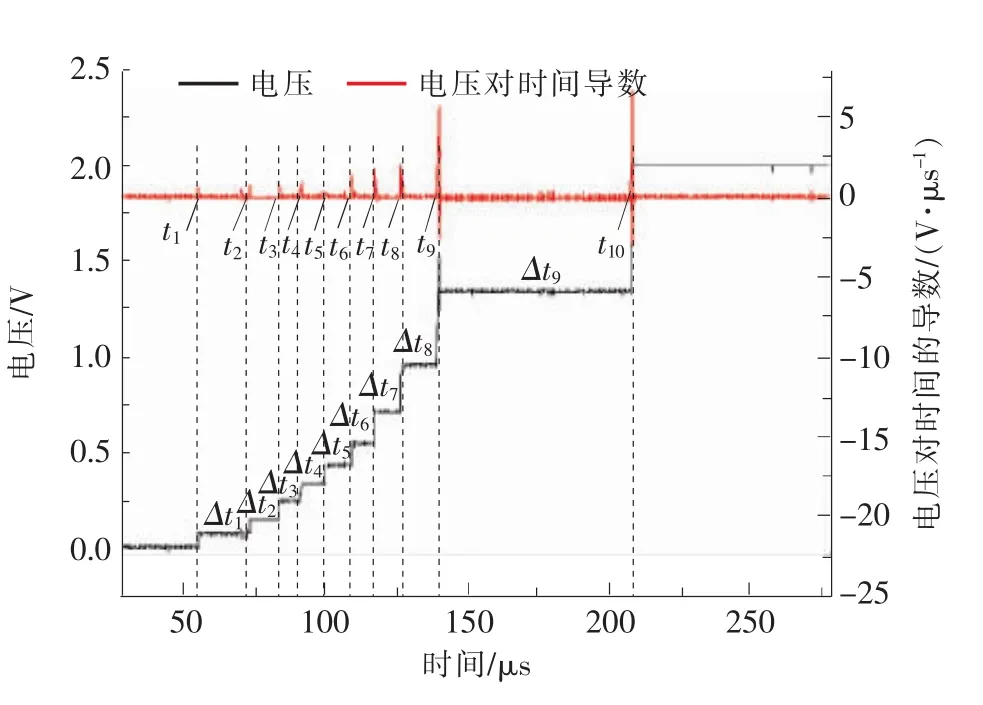
图8　SENB-01试样裂纹扩展计两端电压以及电压对时间导数

由图8已知t1～t10和Δt1～Δt9的值，另外，CPG相邻2根敏感栅丝间的距离l0=1.11 mm是确定的，则可得到t1～t10每个时刻裂尖的位置，并且由νai=l0/Δti（i=1，2，…，9）可得到Δt1～Δt9各个时间段内裂纹的扩展速度，如图9所示。

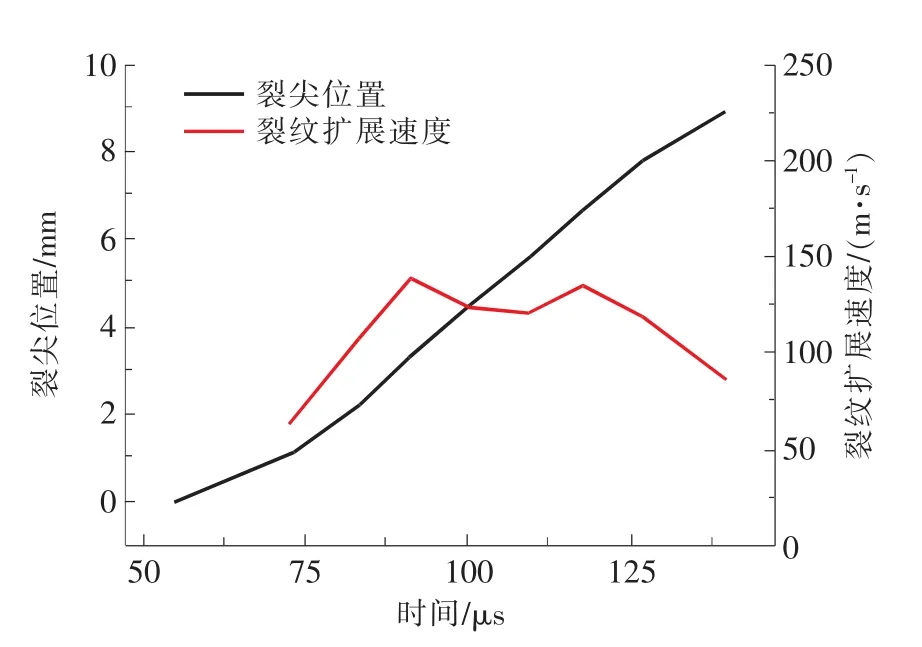
图9　SENB-01试样的裂尖位置以及裂纹扩展速度

由图9可得SENB-01试样的裂纹扩展速度并非是均匀的，而是呈现一定的震荡性，这主要是由材料本身的不均匀性引起。从图9可以看出，SENB-01试样的最大裂纹扩展速度为νmax=138.75m/s，最小速度为νmin=62.71m/s，平均速度为νave=111.92m/s。

3　动态J积分的数值计算

为了使测试材料动态断裂韧度的工作简单易行，易于标准化，有很多学者致力于寻求三点弯曲试样动态应力强度因子的近似公式［11］。本文基于ANSYS软件编制了APDL命令流，结合实验得到的载荷时程曲线，对实验过程进行数值模拟。

根据SENB试样的对称性，建立如图10所示的1/2平面模型。模型采用PLANE42平面应变单元，共有1000个单元和1071个节点。根据实验中SHPB对SENB的加载情况，将试样入射端进行载荷加载方向的位移耦合，将试样对称面的约束设置为对称约束，将试样支撑点进行位移耦合并设置为固定约束。

图10　SENB试样的1/2有限元模型

在二维平面问题中，J的表达式可表示为

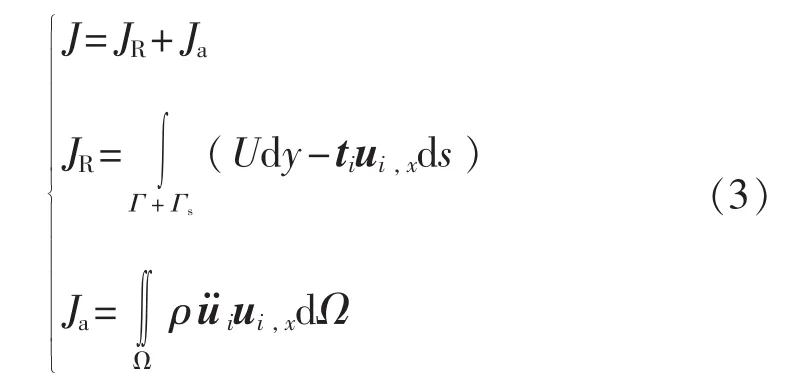
式中，JR为Rice J R［12］于1968年首次提出的积分，Ja是本文根据雷和荣［13］，Kishimoto K［14］，Nishioka T［15］等的工作推导而来，由于论文篇幅所限，推导过程在此不再详述。Γ+Γs是包含裂纹尖端的闭合回路，Ω是Γ和Γs包围的面域，U为单元应变能密度，ti为面力矢量，ui和u¨i分别为位移矢量和加速度矢量，T为单位体积的动能。

Rice.J积分（即JR）可以在ANSYS中定义积分路径后将变量映射到路径上进行操作，此时，求解动态J积分的关键就是要求解出分量Ja。而Ja是一个面积分，不能直接在ANSYS中通过GUI操作实现。因此，本文通过编写APDL命令流来计算Ja项，这样即可用式（3）计算出J积分。如图11所示为APDL命令流计算得到的SENB-01试样J积分响应曲线。

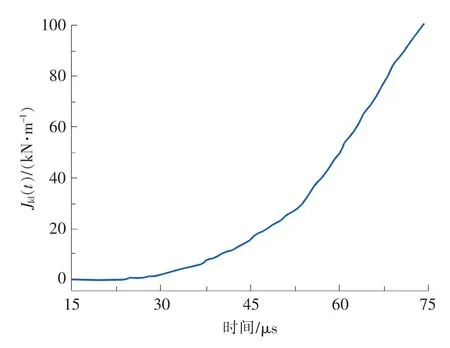
图11　SENB-01试样的J积分响应曲线

4　动态断裂韧度的确定

动态断裂韧度实验研究的重点在于起裂时间的确定，只要确定了起裂时间，则起裂时间所对应的J积分值就是JId。在平面应变条件下，与JId等效的断裂韧度参量KId可采用下式换算：

式中，弹性模量E=37.13GPa，泊松比ν=0.3。

表2所示为SENB试样的实验数据。通过控制气压和入内得到了不同加载速率下SENB试样的起裂时间tf，平均裂速νa，动态起裂韧度KId等信息。动态起裂韧度的确定如图12所示，即通过第3节内容得到J积分响应曲线，然后通过裂纹扩展计记录的信号得到起裂时间tf，则其所对应的J积分值即为JId。再通过式（4），即可得到动态起裂韧度KId。加载速率（˙Id）的计算如下所示：

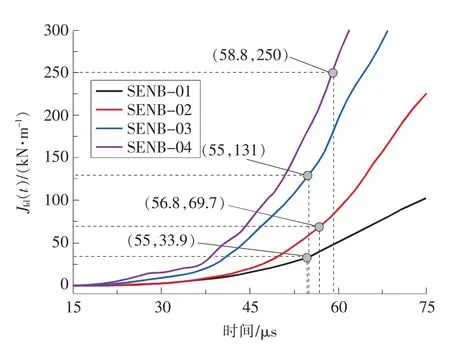
图12　不同加载率下SENB试样的JId确定

表2　SENB试样实验数据

5　结果分析与讨论

5.1CPG与SG测试结果的讨论

为了比较CPG和SG测量裂纹断裂韧度的有效性，在SENB-02试样的两侧分别粘贴CPG和SG，如图13所示。

图13　在SENB-02试样的两侧分别粘贴CPG和SG示意图

如图14所示，为SENB-02试样的CPG和SG的电压信号及入射杆上应变片的电压信号。结合图14及第3节的内容，即可得到J积分响应曲线，如图15所示。

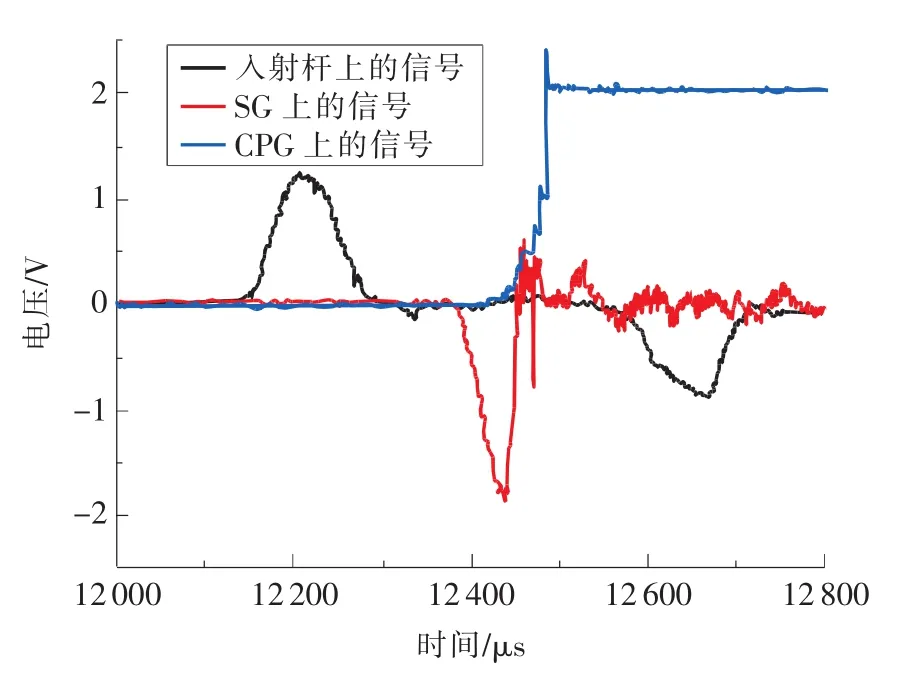
图14　SENB-02试样的电压信号

将图14中的数据经过处理可知，CPG监测到的裂纹起裂时间为tCPG=56.8μs，SG监测到的起裂时间为tSG=58.8μs，两者对应的J积分值即为SENB-02试样的JId，然后通过式（4）即可求得对应的KId，分别为KId-CPG=53.2MPa·m1/2和KId-SG=57.9MPa·m1/2。由此可知，CPG监测到的起裂时间与SG监测到的起裂时间仅相差2μs，对应起裂韧度相差4.7MPa·m1/2，实验结果相当。因此，用CPG测量金属的断裂韧度是可行的，同时，CPG可以监测裂纹的扩展速度，而SG则无法监测。

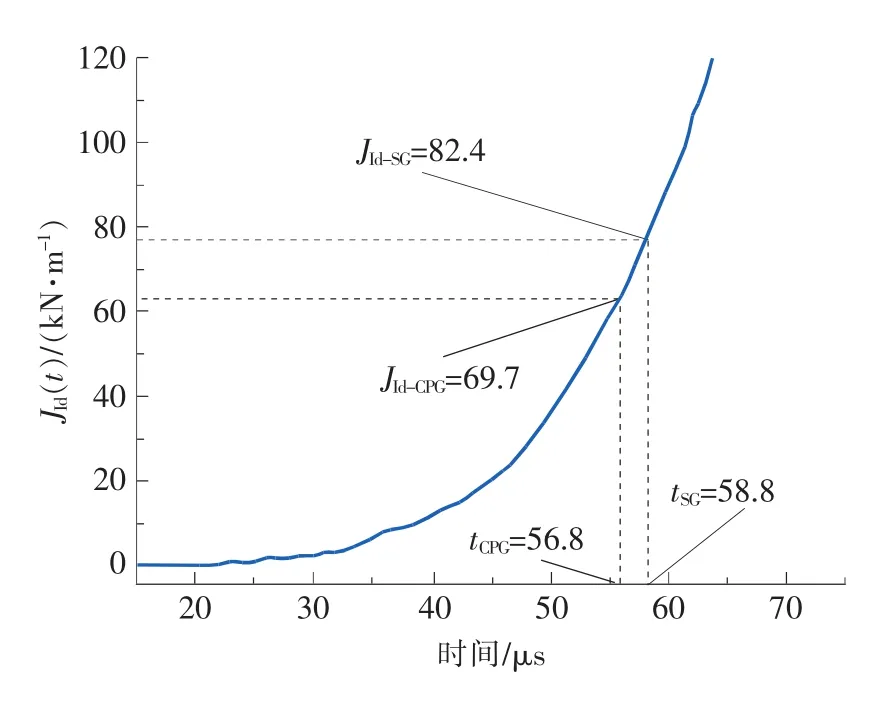
图15　SENB-02试样的J积分响应曲线

5.2加载率对裂纹扩展速度及动态断裂韧度的影响

NiTi合金SENB试样的动态起裂韧度与动态加载率之间的关系如图16所示，本次实验的动态加载率范围为（0.676～1.716）×106MPa·m1/2·s-1。在此范围内，NiTi合金的动态起裂韧度KId随动态加载率K˙Id的提高呈线性增加。由此说明，NiTi合金在动态断裂过程中表现出了明显的率敏感效应，即它抵抗断裂的能力随着加载率的增大而提高。

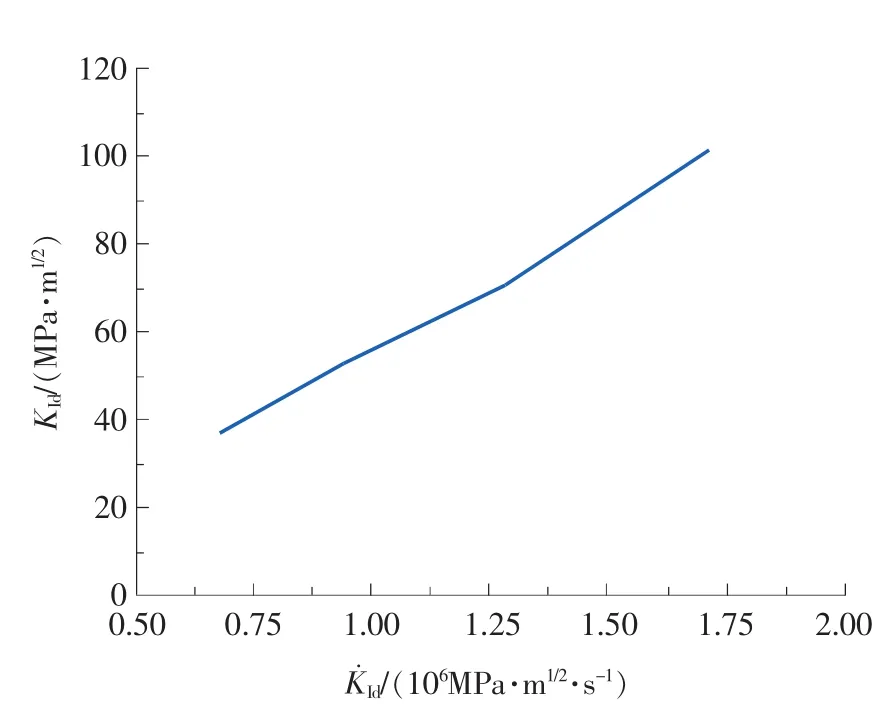
图16　SENB试样的KId-K˙Id曲线

NiTi合金SENB试样动态扩展速度νa与动态加载率K˙Id之间的关系如图17所示。在此次实验加载率范围内，裂纹的扩展速度随加载率的提高而显著增大，并有一定的震荡性。由图可以看出，当加载率在（0.676～1.282）×106MPa·m1/2·s-1范围内时，裂纹扩展速度随加载率的增加而增大的趋势相对缓慢，而当加载率在（1.282～1.716）×106MPa·m1/2·s-1范围内时，裂纹扩展速度随加载率的提高而急剧增大。

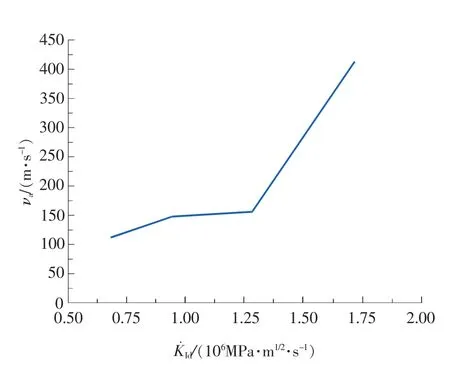
图17　SENB试样νa-Id曲线

综上，NiTi合金在动态载荷下表现出了明显的率敏感效应。图12所示的结果也可证明上述结论的准确性。由图12可以看出，动态应力强度因子随着加载率的升高而增大。本文只是得到了K˙Id与KId、νa之间的定量关系，至于它们之间服从何种定量表达式关系则需要更多的实验数据和理论知识来确定。

6　结束语

1）本文将CPG用于NiTi合金动态起裂韧度、动态扩展速度的测量，得到了不同加载率下NiTi合金的动态断裂参数。并将CPG测得的起裂时间与传统监裂应变片测得的结果进行了对比，两者起裂时间仅相差2μs，由此表明将CPG用于测量金属SENB试样的断裂参数是完全可行的。

2）NiTi合金是率敏感材料，其起裂韧度、裂纹扩展速度均随加载速率的提高而增大，在（0.676，0.937，1.282，1.716）×106MPa·m1/2·s-14个加载率下，NiTi合金的起裂韧度、裂纹扩展速度分别为（37.2，53.2，70.5，100.9）MPa·m1/2和（111.9，148.25，154.9，412.67）m·s-1。

3）鉴于NiTi合金是率敏感材料，在特殊服役环境下（如航空、航天等）设计、选材和安全评定时均应对该合金进行动态力学性能测试。

［1］阚前华，康国政，钱林茂，等.超弹性NiTi合金相变棘轮行为的实验研究［J］.金属学报，2008，44（8）：949-955.

［2］TANAKA K，KAGATSUME T.Impact bend test on steel at low temperatures using a split Hopkinson bar［J］. BulletinoftheSeismologicalSociertyofAmerica，1980，185（23）：1736-1744.

［3］BERGER J R，DALLY J W，DEWIT R，et al.Strain gage analysis of fracture in wide plate tests of reactor grade steel［J］.Journal of Pressure Vessel Technology，1993，115（4）：112-117.

［4］李玉龙，刘元镛.用弹簧质量模型求解三点弯曲试样的动态应力强度因子［J］.固体力学学报，1994（1）：75-79.

［5］张晓欣，刘瑞堂.某船用钢动态弹塑性断裂韧性的试验测试［J］.实验力学，2002，17（2）：153-159.

［6］杨井瑞，张财贵，周妍，等.用SCDC试样测试岩石动态断裂韧度的新方法［J］.岩石力学与工程学报，2015，34（2）：279-292.

［7］陈华燕，曾祥国，李星，等.利用实验和数值结合的方法测量镁合金AZ91动态断裂韧性［J］.四川大学学报（工程科学版），2013，45（6）：149-152.

［8］XU T，STEWART R，FAN J，et al.Bridging Crack Propagation at the Atomistic and Mesoscopic Scale for BCC-Fe with Hybrid Multiscale Methods［J］.Engineering Fracture Mechanics，2016（155）：166-182.

［9］PEI L，LU C，TIEU K，et al.Ductile-to-brittle fracture transition in polycrystalline nickel under tensile hydrostatic stress［J］.Computational Materials Science，2015（109）：147-156.

［10］刘德顺，李夕兵.冲击机械动力学与反演设计［M］.北京：科学出版社，1999：30-31.

［11］卢芳云.霍普金森杆实验技术［M］.北京：科学出版社，2013：236-237.

［12］RICE J R.A path 2 independence integral and the approximate a analysis of strain concentration by notches and cracks［J］.JAppl Mech，1968（35）：376-386.

［13］雷和荣，虞吉林.虚裂纹扩展法计算J积分的研究［J］.中国科学技术大学学报，1994，24（2）：207-213.

［14］KISHIMOTO K，AOKI S，SAKATA M.Dynamic stress intensity factors using J-integralandfiniteelements method［J］.Eng Fract Mech，1980（13）：387-394.

［15］NISHIOKA T，ATLURI S N.Path 2 independent integrals，energyreleaseratesandgeneralsolutionsof near-tip fields in mixed-mode dynamic fracture mechanics［J］.Eng Fract Mech，1983（18）：1-22.

（编辑：李妮）

The study of experimental and numerical methods for dynamic fracture process of NiTi alloy

HAN Tixin，ZENG Xiangguo，GUO Yang，YANG Xin，CHEN Huayan，LI Yang
（College of Architecture and Environment，Sichuan University，Chengdu 610065，China）

To obtain a quantitative change rule between the dynamic initial fracture toughness，dynamic crack propagation speed and dynamic loading rate of NiTi alloy，an impact loading test was conducted on single edge notched three-point bending（SENB）specimens with the split Hopkinson pressure bar（SHPB）test system based on the experimental-FEM method to figure out the variation rules of dynamic fracture parameters of NiTi alloy.The time of crack initiation and the crack extension speed were measured by the crack propagation gauge（CPG）pasted near the crack tip of the specimen.It is feasible to measure the initiation fracture toughness and crack propagation speed of Type I NiTi alloy by taking the aforementioned method.According to the test results：the crack initiation time displayed on the CPG is roughly in line with the result on the crack strain gage pasted on the same specimen.So the CPG can be used as crack strain gage，which can also measure the fracture toughness of NiTi alloy.In addition，the dynamic crack propagation process can be obtained with the CPG.According to the dynamic crack propagation process，the relation curve between crack propagation speed and time can be drawn out.In this way，thequantitativechangerulebetweenthedynamicfracturetoughness，dynamiccrack propagation speed and dynamic loading rate of NiTi alloy can be worked out.

SHPB system；numerical method；NiTi alloy；crack propagation gauge；dynamic fracture process

A

1674-5124（2016）10-0072-07

10.11857/j.issn.1674-5124.2016.10.014

2016-04-10；

2016-05-25

国家自然科学委员会与中国工程物理研究院联合基金项目（U1430119）

韩悌信（1991-），男，甘肃兰州市人，硕士研究生，专业方向为材料疲劳与破坏。