天然边水水域分层水侵量的计算方法

张吉群，邓宝荣，胡长军，常军华，李心浩，李华，和冬梅

（1. 北京科技大学；2. 中国石油勘探开发研究院；3. 中国石油规划总院）

天然边水水域分层水侵量的计算方法

张吉群1，邓宝荣2，胡长军1，常军华2，李心浩2，李华2，和冬梅3

（1. 北京科技大学；2. 中国石油勘探开发研究院；3. 中国石油规划总院）

为了科学、客观地评价具有较大天然水域油藏的开发效果和储集层分层动用状况，改进天然边水水域分层水侵量大小的计算方法，基于多种地质和单井数据，在任意形状的油水界面上部署虚拟注水井，进而模拟天然水域的水侵过程。虚拟注水井部署越密，模拟水侵过程越准确。用判别虚拟注水井与采油井间分层一线连通关系的方法，计算天然水域的水侵方向和水侵阻力。用水电相似原理计算每小层水侵阻力和油藏总水侵阻力，进一步计算每小层的水侵量。将所编制的软件应用于大港、辽河、冀东等10多个油田区块，应用效果表明对于利用天然边水能量开采的油藏，该方法能够更加准确地劈分计算分层水侵量。图8表1参11

边水油藏；分层水侵；水侵方向；水侵阻力；水侵量；一线连通

0 引言

油藏开发经验表明，很多油藏与外部的天然水域相连通，可能是具有外缘供给的敞开水域，也可能是封闭性的有限边水、底水。有些油藏的天然水域较大，具有充分的能量，对油藏的开发动态产生较大的影响，因此对天然水域的水侵量进行分层量化具有重要意义。在油藏开发过程中，随着原油和天然气的采出，油藏内部的地层压力下降，压降必将逐步向外部天然水域以弹性方式传播，并引起天然水域内的地层水和储集层岩石的弹性膨胀。在天然水域与油藏地层压差作用下，会造成天然水域的水侵入油藏［1-2］。由于油水井的生产状况、射孔层位和射孔厚度的不同，油藏内部各小层的地层压力下降程度不同。各小层的岩石物性和流体物性的不同导致侵入水在各小层的渗流能力差异较大；由于天然水域与油藏在各层油水界面的几何形态不同，导致天然水域的水侵方向不同，造成天然水域与油藏各层之间的地层压差不同，进而导致天然水域向油藏各层的水侵量有显著的差别。水侵量越大的层，采油井在该层的产液量越高。

近年来，各油田应用多种劈分算法对采油井的产液量和产油量进行劈分。由于天然水域流向油藏各小层的水侵量不同，导致各小层的天然能量补给不同。为准确地劈分采油井分层产量，应当考虑天然水域在各小层的水侵量大小。

目前，国内外对油藏整体天然水侵量的计算方法已有成熟的研究成果［1-2］，但对天然水域分层水侵量的计算尚未在文献中见到。

本文综合采用10多种数据，考虑多种因素，应用计算几何、渗流力学、油藏工程等多学科理论，提出了一种计算各小层历年水侵量的方法，从而可以更加科学、客观地评价具有天然水域油藏的开发效果。

1 计算分层水侵量的基础数据和基本原理

1.1 基础数据

为了计算分层水侵量大小，必须有以下基础数据：①油藏岩石和流体物性数据；②单井小层物性数据（渗透率、有效厚度、砂岩厚度、砂岩的顶底深等）；③采油井的月井史数据；④措施类数据（射孔、补孔、封堵、压裂等）；⑤产液剖面；⑥边界类数据（砂体边界、油砂体边界、尖灭、泥岩、断层边界）；⑦天然水域的几何形状和大小及岩石和流体物性数据。

1.2 基本原理

本文研究的天然水域为边水，且水域比较大。应用天然水域水侵量经典计算方法可计算出油藏历年的累计水侵量，再计算出每小层水侵量的比例，从而得到每小层的水侵量。

如果相对多的油井有产液剖面数据，则可根据产液剖面数据计算油井每小层的产液量比例。根据每小层产液量比例和油藏累计水侵量计算出油藏每个小层的水侵量。如果较少采油井有产液剖面数据，且历年的分层测压数据较少，本文提出用虚拟注水井来模拟天然水域的水侵过程。通过计算虚拟注水井与采油井间的水侵方向和水侵阻力，进而计算出每小层的水侵量比例，最终计算出每小层的水侵量，计算流程图见图1。

图1 计算天然边水水域分层水侵量大小算法流程图

因为使用产液剖面计算分层水侵量的方法较为简单，本文仅介绍没有足够产液剖面可用的情况下应用虚拟注水井来计算分层水侵量的方法。

2 分层水侵量计算方法

2.1 确定虚拟注水井的位置

在计算天然边水水域分层水侵量之前，首先由地质建模水体模型得到天然水域的每小层的几何形态。

图2 虚拟注水井位置示意图

部署虚拟注水井主要是为了模拟天然水域中水侵的过程。每1口虚拟注水井模拟1小段油水界面对应的天然水域，因此虚拟注水井部署在油藏与天然水域的油水界面上，这样可以保证部署的虚拟注水井能有效地模拟天然水域的几何形状。虚拟注水井部署得越密，模拟油水界面的几何形状及水侵过程的准确性就越高（见图2）。图2中虚拟注水井vi可模拟xi-1至xi段油水界面的水侵过程。

虚拟注水井部署的方法步骤（见图3）为：①设定相邻2口虚拟注水井之间的最大距离Dmax；②得到油水界面的顶点坐标位置（见图3b）；③在油水界面的顶点坐标上部署虚拟注水井（见图3c）；④计算相邻2口虚拟注水井之间的距离Di，i+1，如果Di，i＋1＞Dmax，则这2口虚拟注水井之间需要加密虚拟注水井，否则不需要加密（见图3d）。

图3 部署虚拟注水井

2.2 计算虚拟注水井的物性数据

得到虚拟注水井井位坐标之后，由于虚拟注水井并非真实的井，所有没有小层物性数据（如渗透率、厚度）。应用克里金插值算法［3］，计算虚拟注水井各小层渗透率和厚度数据的方法（其他数据用类似的方法计算）步骤如下：①计算出每口虚拟注水井所在位置各小层的厚度和渗透率，如图2中vi位置各小层的厚度和渗透率；②计算出每两口相邻虚拟注水井中点位置各小层的厚度和渗透率，如图2中xi-1和xi位置各小层的厚度和渗透率；③应用（1）式、（2）式，计算虚拟注水井所模拟的油水界面处各小层的厚度和渗透率，即图2中红色线部分的厚度和渗透率：

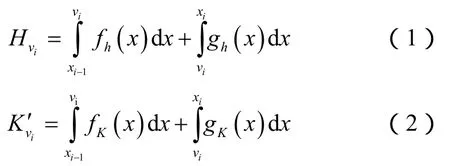
如果按线性插值法，则（1）式变换为（3）式，如果按厚度加权平均法，则（2）式变换为（4）式：

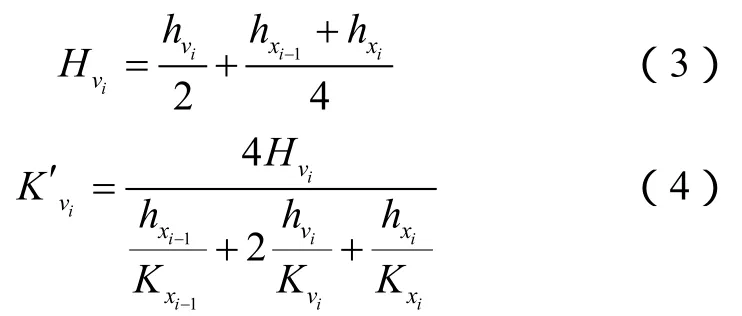
2.3 计算虚拟注水井的水侵方向及水侵阻力

将虚拟注水井作为注水井，运用计算几何算法判别注采井间一线连通关系［4-7］，即水侵方向。在此基础上，计算水侵阻力。水侵阻力与虚拟注水井和采油井间的渗透率、有效厚度、井距、压差等数据有关［2］。阻力越大，水侵量越小。该方法在综合使用多种数据的基础上，充分考虑砂体和断层的形态与展布、油水井的生产动态与射孔封堵措施、井网分布等多种因素，应用计算几何算法和渗流力学理论，计算出历史上各日期、以层为单位的各井组注水流向及各方向的水流阻力，计算结果见图4。图5、图6为径向流和直线流多油层油藏的水侵方向和水侵阻力。

图4 某小层某时刻的水侵方向和水侵阻力示意图

2.4 计算每小层及区块的水侵阻力

根据水电相似原理［8-9］，计算每小层的水侵阻力和油藏的总水侵阻力。

图5 径向流油藏水侵方向和水侵阻力示意图

图6 直线流油藏水侵方向和水侵阻力示意图

2.4.1 计算每小层水侵阻力

由每小层的所有虚拟注水井与采油井的一线水侵连通关系（一线水侵连通关系为强连通关系，二线水侵连通关系为弱连通关系，本文仅考虑强连通关系）和水侵阻力，计算每小层的水侵阻力（见图7）：

图7 计算油藏各层以及总水侵阻力

2.4.2 计算区块的总水侵阻力

由每小层的水侵阻力，应用水电相似原理，计算区块的总水侵阻力（见图7）：

2.5 计算油藏累计水侵量

计算油藏累计水侵量有以下3种方法［1-2］。

2.5.1 经典公式计算累计水侵量（方法1）

2.5.1.1 稳态流的计算方法

Hrust于1943年修正了Schilthuis于1936年得到的稳定流的天然水侵量的公式［1-2］，即：

2.5.1.2 非稳态流的平面径向流和半球形流的计算方法

应用Van Everdingen和Hurst法，可以计算出非稳态流的平面径向流和半球形流的天然累计水侵量［1-2］，即：

2.5.1.3 非稳态流的直线流的天然累计水侵量的计算方法

应用Nabor和Barham法，计算非稳态流的直线流的天然累计水侵量［1-2］，即：

2.5.2 经验公式计算累计天然水侵量（方法2）

由于方法1的（7）—（9）式中部分参数难以得到，应用胜利油田地质科学研究院总结的经验公式计算累计天然水侵量［1］。

2.5.3 根据油藏物质平衡方程计算累计天然水侵量（方法3）

由于天然水域的几何及物性参数不容易获得，因此方法1不易使用。方法2的经验公式为近似取值，误差相对较大。本文实例应用方法3计算油藏累计水侵量。此外，还可应用文献［10］、［11］两种方法计算油气藏水侵量［10-11］。

2.6 计算每小层的水侵量

根据油藏总水侵阻力以及每小层的水侵阻力，计算出每小层的水侵量比例系数：

再根据该比例系数和油藏累计水侵量，最终计算出每小层在任意时刻的水侵量：

3 应用实例

本文方法已用于10多个区块，仅以中国东部油田某复杂断块油藏为例。该区块共有8个小层，地质储量321.878×104t，原始地层压力为34.012 MPa，1991年的地层压力为30.298 MPa，原油密度为0.91 g/cm3，原始原油体积系数为1.381 2，地层水压缩系数为4.35×10-4MPa-1，地层压缩系数为4.97×10-4MPa-1，地层束缚水饱和度为28%，油水界面半径均为1 050 m，水侵圆周角为360°，油水界面到天然水域外缘的长度7 350 m，天然水域有效孔隙度22.78%，有效厚度为52.26 m。到1991年，区块累计产油量为21.260 9×104t，累计产水量为7.857 8×104m3。由于油藏边水活跃，在无注水开发时期，有部分采油井的含水已经达到50%。图8为该油藏4个小层的虚拟井部署情况以及1991年时虚拟注水井的水侵方向。

根据1991年虚拟注水井水侵方向和水侵阻力，利用（5）式、（6）式、（11）式计算出该时期各层水侵阻力、总水侵阻力以及各层的水侵比例系数，计算结果见表1。

图8 虚拟注水井部署位置和1991年虚拟注水井水侵方向

根据物质平衡方程即（12）式计算截至1990年和1991年底油藏累计水侵量分别为23.369 9×104m3和37.720 1× 104m3，进而得到1991年水侵量为14.350 2× 104m3。最后用水侵比例得到各层的水侵量，计算结果见表1。

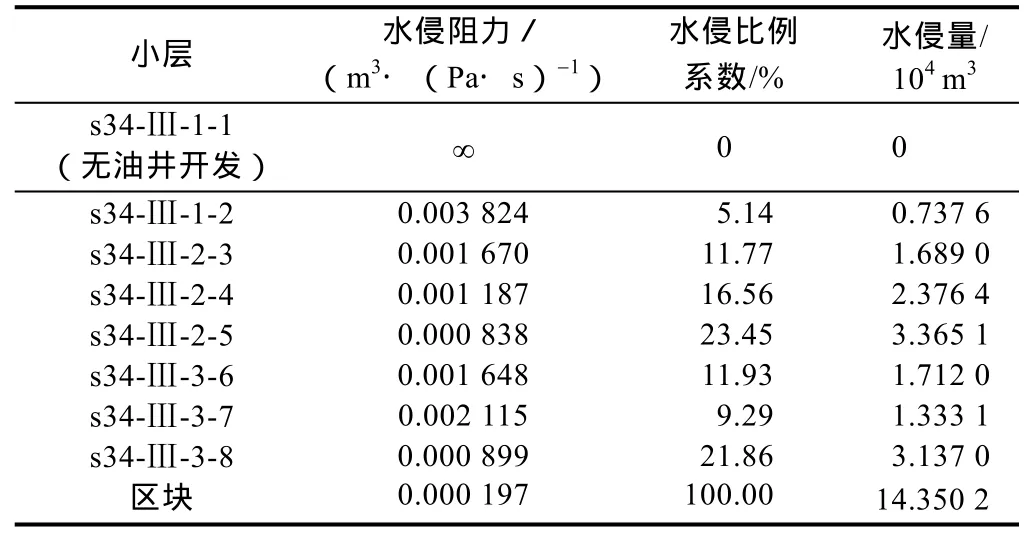
表1 各小层在1991年的水侵量

4 结论

本文提出了一种天然边水水域分层水侵量的计算方法，该方法使用虚拟注水井模拟天然水域的水侵过程，把虚拟注水井部署在油藏与天然边水的油水界面上，再根据油藏历年的累计水侵量以及各层虚拟注水井与采油井间水侵阻力计算每小层水侵阻力，最终计算出每层水侵量。

该方法在10多个油藏区块得到应用，计算结果得到油田开发人员的认可。实例证明，该方法具有准确性与高效性的统一，可计算各种地质条件下天然边水水域分层水侵量的大小，为量化分层开采效果、确定纵向动用程度提供了可靠的研究手段。

部署虚拟注水井的多少直接影响每层水侵阻力的大小，进而影响模拟水侵的过程，因此虚拟注水井部署越密，模拟油水界面的几何形状及水侵过程的准确性就越高，计算结果就越准确。

符号注释：

a——与时间无关的换算常数；b——天然水域的宽度，m；Bg——压力p下的天然气体积系数；Bgi——原始天然气体积系数；Big——压力p下的注入气体体积系数；Bo——压力p下的地层原油体积系数；Boi——原始地层原油体积系数；Bw——压力p下的地层水的体积系数；Ce——天然水域内地层水和岩石的有效压缩系数，MPa-1；Cf——地层岩石的有效压缩系数，MPa-1；Ch——Hurst水侵常数，104m3/（MPa·d）；Cw——地层水的压缩系数，MPa-1；Di，i+1——第i，i+1口虚拟注水井间的距离，m；Dmax——相邻两口虚拟注水井间的最大距离，m；fh（x），gh（x）——xi-1至vi，vi至xi的油水界面处各小层的厚度变化函数；fK（x），gK（x）——xi-1至vi，vi至xi的油水界面处各小层的渗透率变化函数；Gi——地面人工注气量，104m3；h——天然水域有效厚度，m；位置的各小层厚度，m；——xi位置的各小层厚度，m；位置的各小层厚度，m；模拟的油水界面处各小层的厚度，m；i——小层序号；j——虚拟注水井序号；位置的各小层渗透率，μm2；位置的各小层渗透率，μm2；位置的各小层渗透率，μm2；模拟的油水界面处各小层的渗透率，μm2；Lw——油水界面到天然水域外缘的长度，m；m——气顶区的天然气地下体积与含油区的原油地下体积比；n——t时刻第i小层的水侵连通关系总数；N——含油区内原油的原始地质储量（地面标准条件），104m3；Np——地面的累计产油量，104m3；pi——原始地层压力，MPa；p——油藏开采到t时刻的地层压力，MPa；Δp——地层压降，MPa；Δpe——油藏内边界上（即油藏平均）的有效地层压降，MPa；Q——无因次水侵量；Qet——t时刻油藏区块水侵量，104m3；Qeit——t时刻第i小层水侵量，104m3；r——虚拟注水井与采油井间分层水侵阻力，m3/（Pa·s）；rijt——t时刻第i小层第j个水侵连通关系水侵阻力值，m3/（Pa·s）；rwoc——油水界面半径，m；rD——无因次半径；Rit——t时刻第i小层的水侵阻力，m3/（Pa·s）；Rt——油藏总水侵阻力，m3/（Pa·s）；Rp——累计生产气油比，m3/m3；Rs——压力p下的溶解气油比，m3/m3；Rsi——原始溶解气油比，m3/m3；s——油藏小层数；t——某一时间，d；tmax——油藏开发的最长时间，d；tD——无因次时间；Swi——地层束缚水饱和度，%；vi——第i口虚拟注水井；vi+1——第i+1口虚拟注水井；vi-1——第i-1口虚拟注水井；We——累计天然水侵量，104m3；Wet——t时刻区块累计水侵量，104m3；We，t-1——t-1时刻区块累计水侵量，104m3；Wi——地面累计人工注水量，104m3；Wp——地面累计产水量，104m3；xi-1——第i-1口虚拟注水井与第i口虚拟注水井的中点；xi——第i口虚拟注水井与第i+1口虚拟注水井的中点；θ——水侵的圆周角，（°），平面径向流该值为360°；λit——t时刻第i小层水侵比例系数；φ——天然水域的有效孔隙度，%。

［1］陈元千，李璗. 现代油藏工程［M］. 北京: 石油工业出版社，2001. CHEN Yuanqian，LI Dang. Modern petroleum reservoir engineering［M］. Beijing: Petroleum Industry Press，2001.

［2］秦同洛，李璗，陈元千. 实用油藏工程方法［M］. 北京: 石油工业出版社，1989. QING Tongluo，LI Dang，CHEN Yuanqian. Practical reservoir engineering method［M］. Beijing: Petroleum Industry Press，1989.

［3］Environmental Protection Agency. Disjunctive Kriging program for two dimensions［M］. US: BiblioGov，2013.

［4］ZHANG Jiqun，HU Changjin，DENG Baorong，et al. The application of computational geometry algorithms in discriminating direct injection-production connections［C］//2015 International Conference on Materials Engineering and Information Technology Applications（MEITA 2015）. Paris: Atlantis Press，2015: 635-642.

［5］BERG M D，CHEONG O，KREVELD M V，et al. Computational geometry［M］. Berlin: Springer，2007.

［6］PREPARATA F P，SHAMOS M L. Computational geometry: An introduction［M］. Berlin: Springer，1993.

［7］周培德. 计算几何: 算法分析与设计［M］. 4版. 北京: 清华大学出版社，2011. ZHOU Peide. Computational geometry: Algorithms analysis and design［M］. 4th ed. Beijing: Tsinghua University Press，2011.

［8］张建国，杜殿发，侯健，等. 油气层渗流力学［M］. 东营: 中国石油大学出版社，2009: 126-133. ZHANG Jianguo，DU Dianfa，HOU Jian，et al. Percolation mechanics of oil and gas reservoir［M］. Dongying: China University of Petroleum Press，2009: 126-133.

［9］葛家理. 现代油藏渗流力学原理［M］. 北京: 石油工业出版社，2003. GE Jiali. The modern mechanics of fluids flow in oil reservoir［M］. Beijing: Petroleum Industry Press，2003.

［10］潘克家，谭永基，王才经. 自动识别油藏边界水侵量微分方程反演算法［J］. 石油学报，2008，29 （5）: 747-751. PAN Kejia，TAN Yongji，WANG Caijing. Inversion algorithm of differential equation for automatically identifying water influx of reservoir boundary［J］. Acta Petrolei Sinica，2008，29 （5）: 747-751.

［11］姚翔，董杰，杨慧，等. 基于物质平衡和水侵量的边水容量计算［J］. 油气地球物理，2013，11 （2）: 60-67. YAO Xiang，DONG Jie，YANG Hui，et al. Edge water capacity calculation based on material balance and the water influx［J］. Petroleum Geophysics，2013，11 （2）: 60-67.

（编辑 张敏）

Computation method for water influx in different layers of natural edge water

ZHANG Jiqun1，DENG Baorong2，HU Changjun1，CHANG Junhua2，LI Xinhao2，LI Hua2，HE Dongmei3
（1. Beijing University of Science and Technology，Beijing100083，China； 2. PetroChina Research Institute of Petroleum Exploration & Development，Beijing 100083，China； 3. PetroChina Planning and Engineering Institute，Beijing100083，China）

To scientifically and objectively evaluate the development effectiveness and separated layer production of favorable natural water edge reservoir and to improve the computation method for volumes of water influx in different layers，this study applies a novel technique to simulate the process of natural water invasion by utilizing various geological and single wells' data and deploying virtual injection wells at the oil-water interface of arbitrary shape. The denser the virtual injection wells are deployed，the more precise the water invasion process can be. This study calculates water influx direction and intrusion resistance of natural edge water by discriminating connection relationship of separated layer between the virtual injection wells and production wells. Referring to hydropower similarity principle，it calculates intrusion resistance of each layer and total invasion resistance of the reservoir，thus deriving the volume of water influx of each layer. The new method has been implemented in software and applied to over ten blocks in Dagang Oilfield，Liaohe Oilfield，Jidong Oilfield，etc. The results have shown that the method is more accurate for split production data to calculate separated layer water influx volume in each unit in natural water edge reservoir.

edge water； water influx in different layers； water influx direction； water intrusion resistance； water influx volume； one-line connection

国家科技重大专项（2008ZX05010-003）

TP301.6

A

1000-0747（2016）05-0758-06

10.11698/PED.2016.05.11

张吉群（1974-），女，吉林长岭人，博士，中国石油勘探开发研究院工程师，主要研究方向为图形及图像学及其在石油工业中的应用。地址：北京市海淀区学院路20号，中国石油勘探开发研究院油气开发软件中心，邮政编码：100083。E-mail：zjqwxs@sina.com

2015-12-07

2016-06-08