基于改进遗传算法的城市交通信号控制

杨永杰

（山西省交通科学研究院，山西 太原 030006）

1 现代城市交通现状

从21世纪初开始，我国经济发展进入快车道，道路交通设备逐渐完善，大量人口集中生活在城镇、大都市之中，随着人数不断上升，车辆运营数量也在增长，导致城市交通超负荷运行。面对世界性的难题，人类的处理方式将对人类文明和近几年倡导的低碳出行产生深远影响。作为道路交通运输的重要组成部分[1]，城市交通存在诸多问题，a）车辆保有量增长迅速，城市车道容量不足；b）城市交通过于平面化，虽然城市交通的建设已经进入快速发展期，但是仍赶不上车辆增长速度；c）城市道路规划与建设不合理，交通管控能力不强。公路干道距离大、缺少旁路、砂石路、窄路面较多，交通网循环不畅，乱停、乱放情况严重，交通地图信息服务滞后、交通信号管控能力过于机械化，难以适应现代化城市交通的需要。

针对上述问题，应该在城市建设中加快城市整体公共设施的建设，从最新应用的理论知识中寻找支持，通过采用具有实际实施意义的理论知识，分析现实中存在的突出问题，同时引入更智能化的控制和人性化管理方法[2]，更有效地管理城市交通。

2 城市交通信号控制优化问题分析

城市交通信号控制系统的控制范围由成千上万的路口组成，用同样形式的数学关系来表达各种变量间关系，这种静态的表达方式与一般的静态优化不同，交通控制的优化是动态问题，状态和控制随时间变化，相互之间的关系就是一个非线性函数问题。

对于非线性的函数系统，系统总是在尽最大努力寻找变量之间存在的渐变关系。从理论上来说，变量之间的关系是无法通过单值来确定的，应该通过随机和多值确定对应关系。因此，解决这类问题主要采用办法是对结果不追求精确解，把动态系统近似成静态系统，利用静态算法解决问题，只要得到与最优解近似的解即可。在此前提下，就可以放宽限制，得到理想的结果。

以上处理非线性问题的思路，已经得到了各方的认可。在固定的时间区间内，将系统当作是时不变系统，简化各因素关系，寻求问题的近似解。

3 城市交通信号控制模型

为了缓解城市交通拥堵现状，通过分析道路路口交通流数据，在一个固定时间段内实测某城市道路路口的交通流量数据，建立一个在相关约束条件下的非线性函数模型，假定机动车在路口的延误为d，得到公式：

式中：w、s、d、q、B 分别为有效绿时比、饱和度、车辆平均延时、车流量、周期时长。

以现实生活中的四叉路口为例，计算公式为：

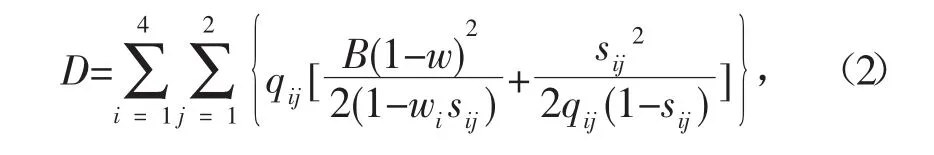
式中：wi、sij、qij分别为某一方位有效绿时比、饱和度、车流量。其中绿灯时间不能小于值g（10 s），满足的条件是：

式中：L为总损失时间。

假定各交叉路口最大饱和度均不大于0.9，则：

式中：yi、fgi分别为车流比、有效时间。

综上所述得到约束条件为：

4 训练过程

为了研究该类型问题，根据交通法规规定：当车辆在路口遇到红灯时车不能直行，可以右转，但不能左转通行。

表1 某四叉路口车流量有关数据表

在表1实测交通流数据的支撑下，假定路口绿灯最短时间为10 s，信号周期时间为B=130，车辆总延误时间为10 s，将表1所示的数据代入建立的数学模型中，由公式（4）得到最短路灯时间：取东向的流量比值代入，得fg1≥25 s，同理其他3个方向取流量比值，得到 fg2≥34 s，fg3≥31 s，fg4≥19 s。代入公式（5），计算出各方向时间ti取值范围，将各计算值代入公式（2），通过迭代数d=50，得到最佳适应度值。

5 简单遗传算法

遗传算法具有很强的全局搜索特性和带有并行运行性的群体遗传学机制。遗传算法的主要操作是对基因进行交叉操作和变异操作。

a）交叉操作 在配对的染色体中，分别截取自身部分基因与对方交换，通过交叉操作来得到新的染色体个体，得到新的种群，提高群体的生存能力。

b）变异操作 对于控制基因采用单个因子变异，改变染色体的物理性状和基因序列，通过变异操作来获得新个体。其目的是保持群体的遗传基因差异，预防出现群体基因近代遗传，获得局部搜索能力。

通过上述介绍，可以得到算法流程图如图1所示。

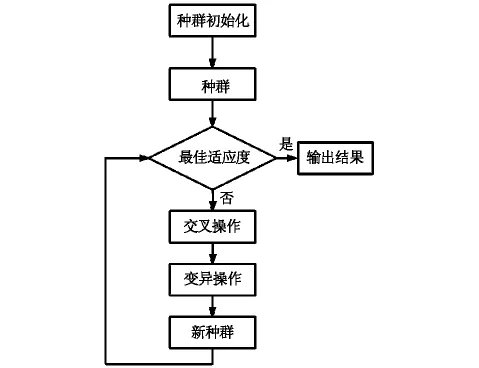
图1 算法流程图

通过交叉和变异操作，利用公式（2）进行计算，得到如图2所示的适应度变化曲线图。

图2 基础遗传算法测定最佳适应度

尽管简单遗传算法有许多优点，但目前存在的问题依然很多，如：

a）简单遗传算法收敛到局部最优解而不是全局最优解。

b）接近最优解时出现左右摆动，收敛较慢。

6 改进遗传算法

通过图2的计算结果可知，算法的收敛性较差，容易陷入局部最优化。为了减小函数误差和简化函数，以提高对群体的选择能力，针对适应度提出公式（6）：

式中：a+b=1 且 0＜a，b＜1；f(i，d)表示个体适应度；T(i，d)表示函数误差；K(i，d)表示函数简化度；d表示迭代数。

随着适应度函数的引入，引入变异率、交叉率的概念。假设变异率、交叉率分别为 Fk、Fm，Fk、Fm的值应随适应度函数的值在变[3]。当适应度低，就选大的Fk、Fm值，选择淘汰该交叉、变异个体；当适应度高，取小的Fk、Fm值，选择保留该交叉、变异个体；保证最优秀的种群[3-6]。基于遗传算法的特点，组建自适应变异函数Fm和自适应交叉函数Fk。通过构造函数，保证算法的收敛性和群体的多样性。

式中：0＜λ1，λ2≤1、λ3≤1、λ4≤1；f为变异个体的适应度;为种群的平均适应度；fmin为当前代中种群的最小适应度；f′为2个交叉个体中较小的适应度。通过公式（7）、公式（8），得到图3所示的适应度值变化曲线图。

通过改进遗传算法，保持了群体多样性的同时，保证了遗传算法的收敛性，更快地得到算法的最优解。

7 结论

图3 改进遗传算法测定最佳适应度

针对城市交通固定时间交通流的特点，以非线性模型为基础，通过改进遗传算法，实现了算法并行性和较强的全局搜索的目的。利用实测的交通流数据进行计算、分析，得到改进的遗传算法收敛性优于简单遗传算法，且不易陷入局部最优。通过改进遗传算法得到的最佳适应度能更好地应用于优化城市交通信号控制建设中。