下穿高速双孔并行隧道可靠度分析
2016-11-15王志勇张美花刘浩
王志勇,张美花,刘浩
(1中铁二院重庆勘察设计研究院有限公司,重庆400023;2重庆文理学院建筑工程学院,重庆402160)
下穿高速双孔并行隧道可靠度分析
王志勇1,张美花2,刘浩1
(1中铁二院重庆勘察设计研究院有限公司,重庆400023;2重庆文理学院建筑工程学院,重庆402160)
针对地下结构可靠度分析中功能函数不能显示表达的特点,提出基于三维有限元的可靠度分析方法。以下穿高速双孔并行隧道为例,根据三维有限元计算结果,分别以DP2与DP3准则作为塑性屈服的判定准则,采用遗传算法选取样本点构建二次响应面模型,通过对Monte Carlo法,基于BP神经网络的Monte Carlo法,中心点法,JC法和遗传算法得出的可靠度指标的比较分析,得出遗传算法的运用可显著提高响应面模型的逼近精度,中心点法计算出的可靠度指标误差较大,Monte Carlo法、BP-Monte Carlo法、JC法及遗传算法求得的可靠度指标精度相近,JC法因操作简便、计算精度高可广泛用于地下结构的可靠度分析。基于遗传算法选取的样本点构建响应面模型,以JC法计算地下结构的可靠度分布,得出在公路线荷载作用下,衬砌上下两侧向内变形,上下两侧围岩应力释放多,可靠度相应增大;衬砌左右两侧向外变形,左右两侧围岩应力增大,可靠度相应减小;并行隧道的相互影响导致邻近另一隧道侧的衬砌可靠度较小。
围岩;可靠度;响应面法;遗传算法;BP神经网络;JC法
0 引言
鉴于实际工程中的诸多不确定因素,工程设计人员提出结构可靠度设计理念。随着城市的不断扩张与发展,居民用地、商业用地等与交通用地的矛盾日益加剧,大中型城市的地铁建设已成为缓解此类矛盾的主要途径之一。自20世纪40年代以来,结构可靠度的研究方法日趋完善,但地下结构的功能函数不能显示表达且难于构造的特征,给地下结构的可靠度计算带来较大困难。
本文在查阅大量文献[1-4],并对可靠度计算方法进行详细分析和总结的基础上。以三维有限元分析为基础,以下穿高速公路双孔并行隧道为例,先利用Monte Carlo法、BP-Monte Carlo、中心点法、JC法及遗传算法计算出并行隧道间围岩单元的可靠度,通过对可靠度指标的比较分析提出一种精度高、操作简便并适用于地下围岩结构可靠度分析的方法。以此方法计算出下穿高速并行隧道围岩及衬砌的可靠度分布,分析双孔并行隧道对围岩与隧道衬砌可靠度分布的影响规律。
1 数学模型
1.1工程概况
并行隧道中心相距13.5m,隧道埋深21m,路堤高4m,防护段边坡坡率1∶1.5。高速与双孔并行隧道上下垂直相交,衬砌为圆形预制钢筋混凝土管片,内径5.4m,外径6m,建立如图1所示的三维模型,模型具体尺寸见图2。

图1 三维模型效果图

图2 模型主要尺寸标注(单位m)
地面交通荷载按照公路—Ⅰ级选取,均布荷载标准值q取10.5kPa,以面荷载形式施加于三维模型行车段表面,集中线荷载标准值Q为180kPa,以线荷载形式施加在隧道左右洞顶上方地表面。
三维有限元分析步骤:
第1步:围岩自重作用下受力平衡;
第2步:路基施工后,自重应力下受力平衡;
第3步:交通荷载作用下受力平衡;
第4步:隧道施工后受力平衡(左右洞室同时开挖,运算1000步后施作衬砌)。
1.2随机参数选取
地下结构可靠度影响因素较多,在简化计算且不影响分析精度的前提下,将变异性较大的参数视为随机变量。考虑地勘设计资料及相关规范,将围岩重度及泊松比,衬砌弹性模量、重度、泊松比等物理力学参数视为定值处理。围岩的弹性模量、粘聚力及内摩擦角,衬砌的粘聚力与内摩擦角视为随机变量,其分布类型及相关分布参数见表1。

表1 随机变量参数取值
1.3模型构建[5-6]
1.3.1功能函数
围岩塑性屈服判定准则采用D-P准则,构建功能函数:


材料常数a和k与材料的粘聚力c和内摩擦角φ有关,采用两种主要的D-P系列修正屈服准则即M-C内角点外接圆准则(DP2)和M-C内切圆准则(DP3),其材料常数a和k与材料的粘聚力c和内摩擦角φ的关系分别如下:
M-C内角点外接圆准则(DP2):

式中的φ为围岩的摩擦角,c为围岩粘聚力。
1.3.2响应面函数
隧道洞室的开挖,破坏了洞室围岩的初始应力平衡状态,导致围岩可靠度下降。根据三维模型随变量波动计算结果,以左侧隧道的右侧围岩单元(图2中的B点)Z值作为功能函数值,构建围岩结构可靠度分析的二次响应面模型为:

式中:xi为随机变量,a0,bi,ci,di等21个未知数为待定常数,需样本点确定,响应面模型逼近精度取决于样本点的选取。随机产生50组随机变量Xi=(x1,x2,x3,x4,x5)i,通过三维有限元计算各变量组对应的功能函数值ZF。从50组随机变量中选取21组随机变量,求解响应面模型的待定常数,以求出的响应面模型求解其余29组变量对应的功能函数值ZX,以此29个功能函数值ZX与三维有限元计算的功能函数值ZF之差的均方差的倒数作为染色体的适应度,通过遗传算法寻求最优组合。进化300代后,DP2的最优个体适应度为130.8447,DP3的最优个体适应度为37.6559,其最优组合求解过程如图3、图4所示。

图3 DP2响应模型拟合进化图

图4 DP3响应模型拟合进化图
2 可靠度分析方法
2.1Monte Carlo法[7]
对基本变量进行N次随机抽样,通过响应面模型计算功能函数值,得到N个功能函数值ZM,如果有Nf个值对应ZM<0,则结构的失效概率就表示为:

2.2基于BP神经网络的蒙特卡洛法[8]
Monte Carlo法计算可靠度指标是以显示表达的功能函数为前提,然而地下围岩结构的功能函数值往往难以显示表示,BP神经网络弥补了Monte Carlo此方面的不足。
创建单隐层的BP神经网络,输入层5个单元,输出层1个单元,隐层11个单元。两层的作用激活函数分别采用双曲正切函数(tansig)和纯线性函数(purelin),训练最大次数为300,训练目标误差为0.001,训练速度为0.01。并以50组随机变量作为输入参数,其对应的功能函数值ZF作为输出参数。以50组随机变量代入训练后的BP神经网络得到的功能函数值ZBP与有限元分析得出的功能函数值ZF之差的均方差评价BP神经网络的拟合效果。
2.3中心点法
中心点法需先将非线性功能函数在随机变量的平均值(中心点)处作Taylor级数展开并保留至一次项,然后近似计算功能函数的平均值与标准差。其可靠度指标可按下式计算得出:

2.4JC法
先对非标准正态随机变量进行当量正态化,当量正态化条件要求在验算点xi*处Xi和Xi’的分布函数和概率密度函数分别对应相等,即
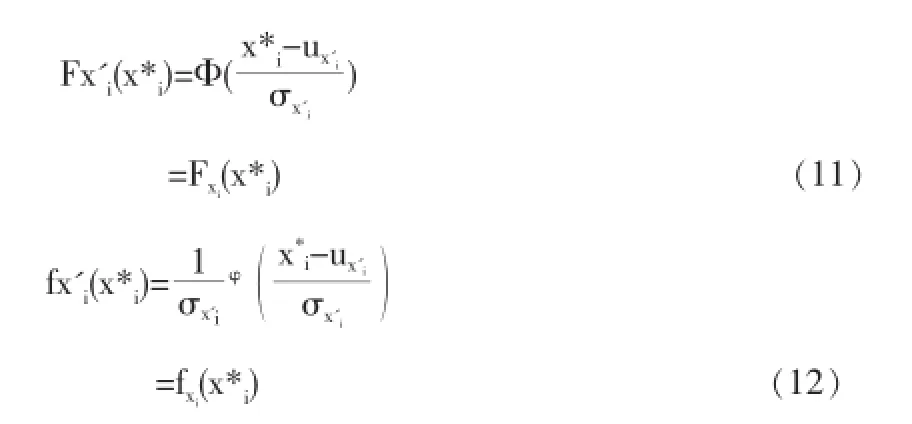
设x*=(x1,x2,…,xn)为满足极限状态函数的一点,即Z=g(x*)=0。在点x*处将极限状态方程Taylor展开并保留至一次项得ZT,则结构的可靠度可以按下式计算:
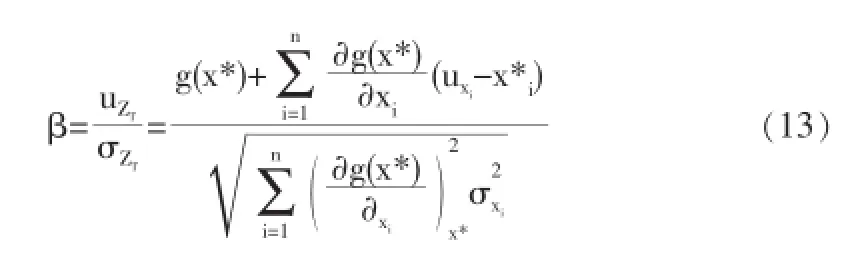
采用映射变换法对对数正态分布的随机变量作当量化处理,则响应面模型中的非标准正态随机分布变量Xi可以用Xi=Fi(Yi)替换,Yi为标准正态随机分布。
2.5遗传算法
由可靠度指标的几何意义得知,可靠度指标就是随机变量标准化空间中原点到极限状态曲面的最短距离,因此求解可靠指标就是求解下面的条件优化问题:
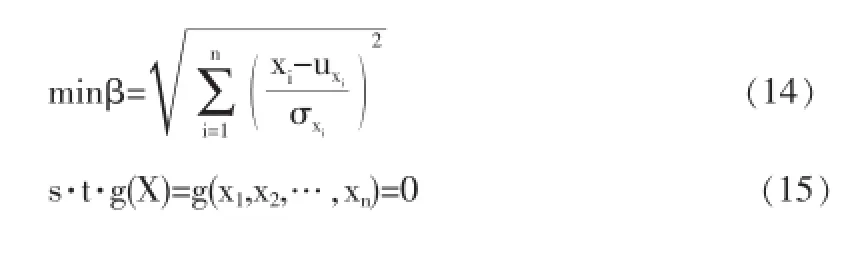
3 成果分析
3.1Monte Carlo法与基于BP神经网络的Monte Carlo法比较
以Monte Carlo法或BP-Monte Carlo法得到的功能函数值ZM或ZBP与数值模拟得出的功能函数值ZF之差的均方差评价各方法的拟合效果。随机产生100万组随机变量,代入响应面模型或训练之后的BP神经网络中求得失效概率,Monte Carlo法与BP-Monte Carlo法的计算结果分别见表2、表3。

表2 BP-Monte Carlo法可靠度指标

表3 Monte Carlo法可靠度指标
因BP-Monte Carlo法计算可靠度时不需构建响应面模型且其拟合精度较高,将BP-Monte Carlo法求出的可靠度指标作为基准值。Monte Carlo法的相对误差小于2%。
基于Monte Carlo法,以遗传算法得到的最不利组合求解响应面模型及失效概率,DP2准则的失效概率为0.3172,DP3准则的失效概率为0.4608。由最优组合与最不利组合求出的可靠度指标比较可知,遗传算法在响应面模型样本点选取中的运用可显著提高二次响应面模型的逼近效果。
DP2准则及DP3准则的选取对Monte Carlo法及BP-Monte Carlo法的可靠度指标影响较小,Monte Carlo法计算出的可靠度相差0.01左右,BP-Monte Carlo法求出的可靠度相差0.1左右。采用DP2准则,Monte Carlo法与基于BP-Monte Carlo法的拟合效果较采用DP3准则时更为精确。
3.2中心点法、JC法与遗传算法的结果比较
响应面模型中的非标准正态随机变量由映射变换后的标准正态随机变量替换,求得JC法及遗传算法的可靠度及相应的失效概率。遗传算法以可靠度的倒数作为染色体的适应度,其进化过程如图5、图6所示。

图5 DP2的可靠度计算进化图

图6 DP3的可靠度计算进化图
中心点法、JC法与遗传算法计算结果分别见表4-表6。

表4 中心点法可靠度指标

表5 JC法可靠度指标

表6 Genetic Algorithm法可靠度指标
中心点法得出的可靠度指标相对误差大,远小于其他方法求出的可靠度指标;JC法得出的可靠度指标相对误差小;遗传算法得出的可靠度指标相对于BP-Monte Carlo法较小。
采用Monte Carlo法、BP-Monte Carlo法及遗传算法虽能达到理想精度,但其操作复杂且计算量巨大;因其本身的局限性,中心点法计算出的可靠度指标误差较大,不具参考价值;JC法操作相对简便,计算精度能满足较高要求。
3.3可靠度分布
DP2作为塑性屈服判定准则,基于遗传算法得出的最优组合,构建二次响应面模型,运用JC法计算可靠度,求出图2所示的A-A剖面围岩(不含路堤)及左侧隧道衬砌的可靠度分布分别如图7、图8所示。
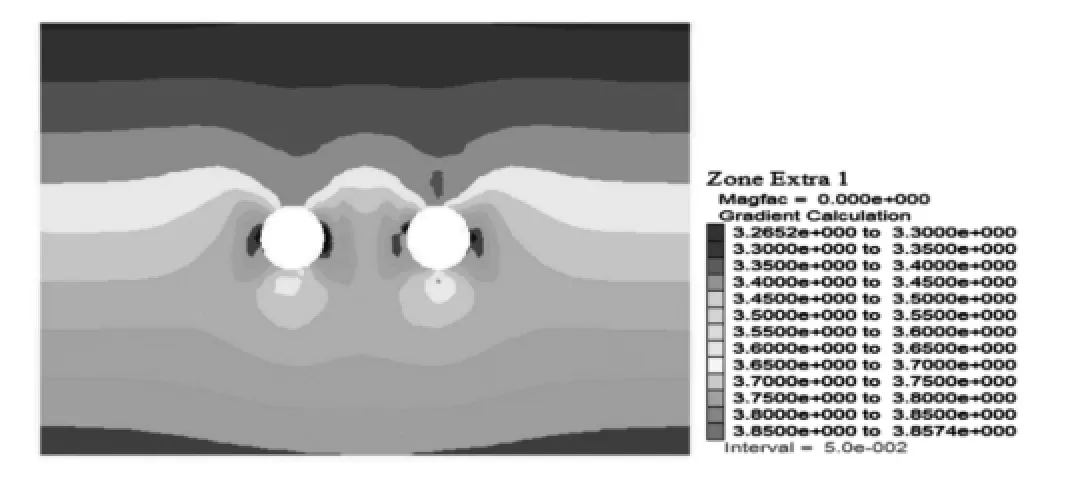
图7 DP2准则对应的围岩可靠度分布(JC法)
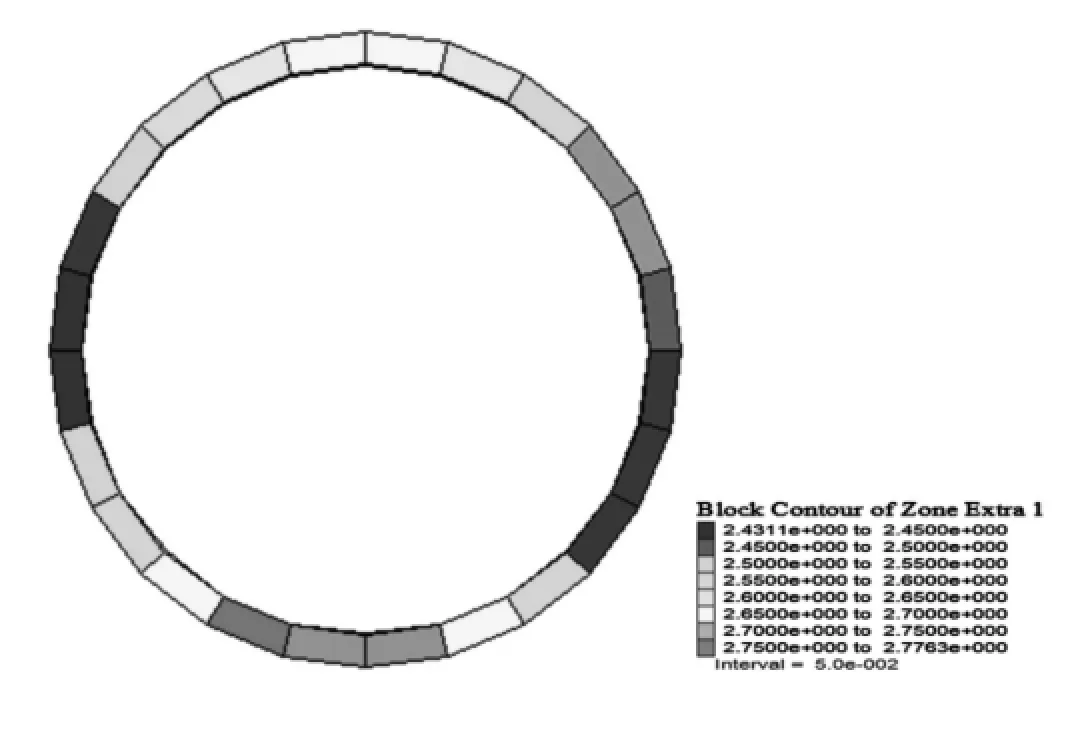
图8 DP2准则对应的左侧隧道衬砌可靠度分布(JC法)
可靠度随着围岩深度的增加而降低,隧道的开挖、公路线荷载的施加等对围岩可靠度造成局部扰动;在隧道开挖与公路线荷载的共同作用下,隧道上下两侧的围岩可靠度相对增大,左右两侧的围岩可靠度指标相对减小。隧道衬砌可靠度最大部位位于衬砌底部左侧,最小区域位于衬砌的左拱腰、右拱脚处。左侧隧道衬砌受右侧隧道的影响,其衬砌右侧部位的可靠度较相对称的左侧部位小。
结合图7的隧道围岩位移状况(拱顶向下移动,仰拱向上移动,左侧围岩向左移动,右侧围岩向右移动)可知:隧道衬砌在公路线荷载作用下由圆环状变形为扁圆环状(上下侧的距离变小,左右侧的距离变大)。上下侧向洞内的移动导致上下侧的围岩应力释放多,由式(1)-(3)知此处围岩单元的功能函数值必将增大,可靠度指标相应增加;左右侧向洞外移动导致左右侧围岩受到挤压,其应力增大,功能函数值减小,可靠度指标相应减小;左右侧隧道之间的围岩因受到左右侧隧道衬砌的共同挤压作用,其可靠度指标相对左侧隧道的左侧围岩与右侧隧道的右侧围岩将会更小。
4 结论
(1)响应面模型的拟合精度取决于样本点的选取,采用遗传算法选取样本点可显著提高响应面模型的拟合精度。
(2)中心点法计算出的可靠度指标相对于其他方法误差较大、应用性不强,JC法得出的可靠度指标与BP-Monte Carlo法较为接近,遗传算法得出的可靠度指标相对较小。
(3)DP2准则与DP3准则的选取对地下洞室围岩的可靠度指标影响较小,构造功能函数时,选取DP2准则可提高响应面模型及BP神经网络的拟合效果。
(4)总体而言,围岩可靠度随埋深的增加而降低,公路线荷载与洞室开挖等会对其造成局部扰动。公路线荷载作用下,隧道衬砌上下两侧受压向洞内变形,围岩应力释放率大,其可靠度增大;隧道衬砌左右两侧向外变形,对围岩形成挤压作用(挤压效果将会在隧道之间的围岩处叠加),其可靠度减小。近并行隧道侧的衬砌受并行隧道的影响导致其可靠度相对于对称部位较小即失效概率大。
[1]陈建康,朱殿芳,赵文谦,等.基于响应面法的地下洞室结构可靠度分析[J].岩石力学与工程学报,2005,24(2):351-356.
[2]颜立新,康红普,高谦.基于响应面函数的可靠度分析及其应用[J].岩土力学,2001,22(3):327-329,333.
[3]徐军,邵军,郑颖人.遗传算法在岩土工程可靠度分析中的应用[J].岩土工程学报,2000,22(5):586-589.
[4]邓楚键,何国杰,郑颖人.基于M-C准则的D-P系列准则在岩土工程中的应用研究[J].岩土工程学报,2006,28(6):735-739.
[5]林峰.基于进化神经网络的可靠度分析及应用[D].长沙:中南大学,2010:1-30.
[6]孙思奥.结构可靠度分析方法及相关理论研究[D].北京:清华大学,2007:10-35.
[7]陈秋莲,王成栋.基于Matlab遗传算法工具箱的优化计算实现[J].现代电子技术,2007,30(2):124-126,129.
[8]曹源,童丽萍,赵自东,等.结构可靠度分析的改进BP神经网络响应面法[A]//第二届结构工程新进展国际论坛论文集[C].2008:795-800.
责任编辑:孙苏,李红
建设信息
工程建设标准深化改革意见出台
日前,住建部印发《关于深化工程建设标准化工作改革的意见》,进一步改革工程建设标准体制,健全标准体系,完善工作机制。按照政府制定强制性标准、社会团体制定自愿采用性标准的长远目标,到2020年,适应标准改革发展的管理制度基本建立,重要的强制性标准发布实施,政府推荐性标准得到有效精简,团体标准具有一定规模。(住建部门户网)
Reliability Analysis of Two Paralleled Tunnels Crossing Beneath a Highway
Considering the difficulty of setting up the performance function in reliability analysis of underground structure,a method based on the 3D-finite element method for reliability analysis is put forth.Taking two paralleled tunnels crossing beneath a highway as an example,the DP2 and DP3 criteria as the norm to judge plastic yield respectively,it builds the quadratic response surface models through the sample points selected by genetic algorithm. Through comparison and analysis of the reliability index calculated by the Monte Carlo,the Monte Carlo based on the BP neural network,center point method,JC method and genetic algorithm,the use of genetic algorithm in selecting sample points can improve the accuracy of the response surface models significantly;the relative error of the reliability indexes calculated by center point method is large;the accuracy of reliability index calculated by Monte Carlo,BP-Monte Carlo,center point method,JC method and genetic algorithm is approximate;JC method can be broadly used in reliability calculation of underground structure for its simple operation and high accuracy.Based on the sample points selected by genetic algorithm to construct response surface models,it draws from the distribution of reliability index of substructure calculated by JC method that under the highway line load the inward deformations of the upper and lower sides of the lining leading to the decrease of stress result in the increase of reliability index of the corresponding sides of surrounding rock and the outward deformations of the left and right sides of the lining leading to the increase of stress result in the reduction of reliability index of the corresponding sides of surrounding rock;the reliability index of the lining near the other tunnel decreases as a result of interaction of the two paralleled tunnels.
surrounding rock;reliability index;response surface method;genetic algorithm;BP neural network;JC method
[TU997]
A
1671-9107(2016)09-0041-05
10.3969/j.issn.1671-9107.2016.09.041
2016-04-29
王志勇(1982-),河北衡水人,研究生,工程师,研究方向为轨道交通与地下工程设计。
