可吸入颗粒物PM2.5的影响因子分析*

朱吉祥，徐　　冉，张　　琳，刘力军

（大连民族学院理学院，辽宁　　大连　116600）

可吸入颗粒物PM2.5的影响因子分析*

朱吉祥，徐冉，张琳，刘力军

（大连民族学院理学院，辽宁大连116600）

运用相关性分析得出了PM2.5与PM10、CO、NO2、SO24项影响因素的相关性，采用多元线性回归方法得到了PM2.5和PM10、CO、NO2和SO2之间的线性回归方程，运用主成分分析方法进行因子分析，结果表明PM2.5与PM10、CO、SO2、NO2呈正相关性。

PM2.5；因子分析；相关性分析

PM2.5是指空气动力学直径小于或等于2.5 μm的颗粒物，虽然PM2.5只是地球大气成分中含量很少的组分，但它对空气质量和能见度等有重要影响，并呈现典型的区域性、复合型污染特征［1-2］。当前以行政单元为主体、孤立的大气污染防治模式难以有效解决PM2.5的污染问题［3］。深入研究PM2.5及其主要影响因素，并在此基础上制定有针对性的控制措施，是控制PM2.5的有效途径。为此，我国开展了PM2.5因素分析的研究。刘辉等［4］的分析表明除污染源排放外，气象条件也是影响PM2.5及其水溶性离子浓度的重要因素。孟昭阳等［5］的研究结果表明：冬季PM2.5、有机碳和元素碳浓度均较高。

笔者使用线性回归法、主成分分析法分析了PM2.5和PM10、CO、NO2、SO2之间的线性相关关系，揭示了不同来源对PM2.5的贡献，进而为PM2.5的治理提出政策性建议。

1　　数据的收集和分析方法

1.1数据来源

数据包含2014年10月1日至2015年3月31日共183 d大连市细颗粒物PM2.5历史数据［6］，每日数据包含PM2.5、PM10、CO、NO2、SO2浓度数据，其部分数据如表1所示。

表1　　大连市细颗粒物PM2.5的部分历史数据

1.2Pearson相关性分析法

n个样本的2个指标xik和xil之间的Pearson相关系数定义为：

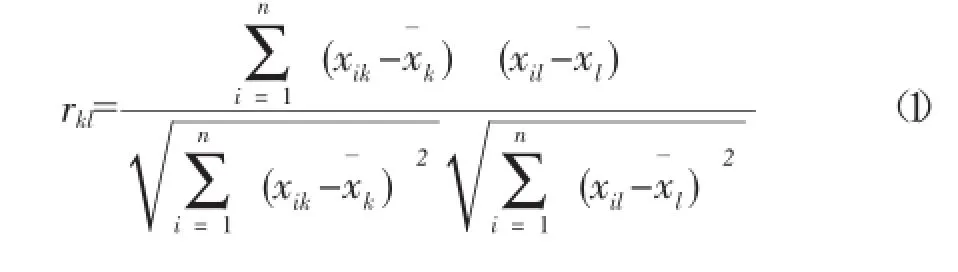
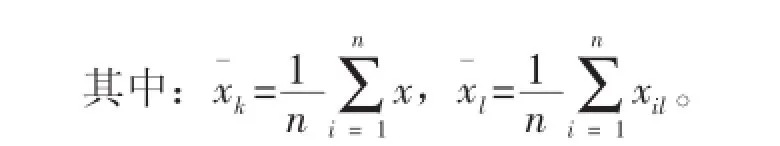
相关系数用来衡量2个数据集合。是否在一条线上，它用来衡量随机变量间的线性关系。Pearson相关系数的r绝对值越大，相关性越强；相关系数越接近于1或-1，相关度越强；相关系数越接近于0，相关度越弱。通常情况下以r的绝对值取值范围判断变量的相关强度，见表2。

表2　　相关系数与相关性强弱关系

2　　分析结果

2.1相关分析和线性回归

运用SPSS以PM2.5与PM10、CO、NO2、SO2的浓度做统计分析，计算出它们的相关系数如表3所示。

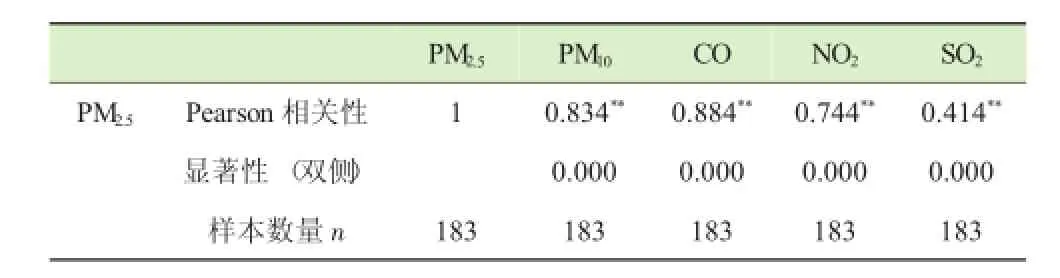
表3　Pearson相关性检验

从表3的Pearson相关系数的计算结果可知，PM2.5与这4项因素具有显著正相关性。

笔者采用多元线性回归方法建立PM2.5与PM10、CO、NO2、SO2的预测模型，其线性回归系数的计算结果和R2分析如表4～6所示。

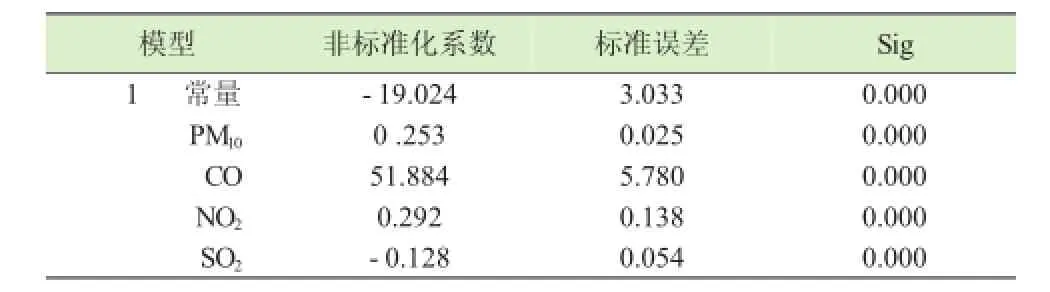
表6　　多元线性方程的回归系数

R2值表明了模型对样本数据的拟合程度，其值越高说明模型对样本数据拟合得更好，表4显示此线性回归模型的拟合度为86.4%，F值是对所有解释变量整体显著性的检验，由表5所示F统计量为289.385，Sig=0.000＜0.005，表明此线性回归模型具有整体显著性。由表6可知，多元线性回归系数分别为0.253、51.884、0.292、-0.128，回归系数常量为-19.024，因此我们得到多元线性方程：

PM2.5=0.253×PM10+51.884×CO+0.292×NO2-0.128×SO2-19.024

图1显示了回归标准化残差的P-P图，可见数据符合正态分布。

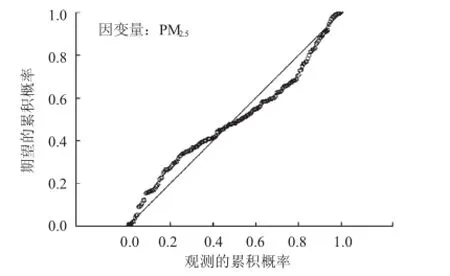
图1　回归标准化残差的P-P图

2.2基于主成分分析方法的因子分析

在得到PM2.5回归方程后，运用主成分分析方法，将这几项因素分别进行降维，可得到它们的碎石图和因子分解图（见图2～3）。

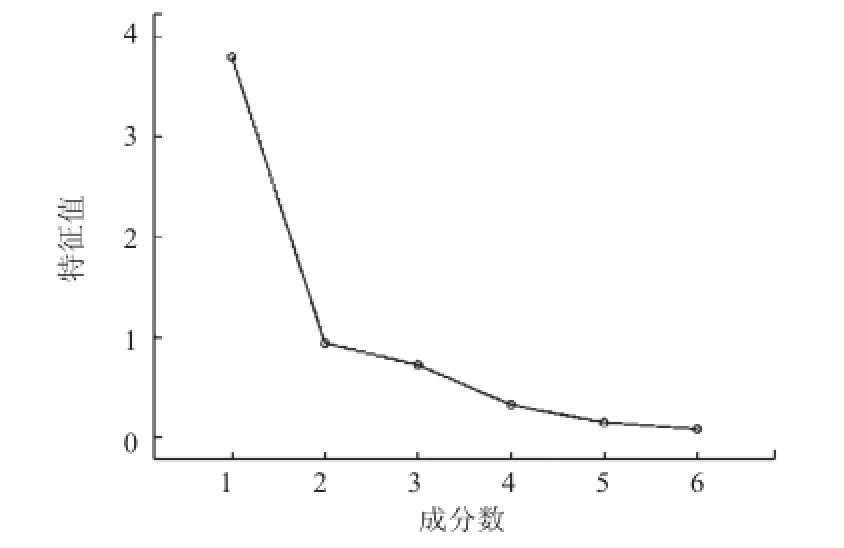
图2　主成分分析的碎石图

表4　模型汇总

表5　方差分析

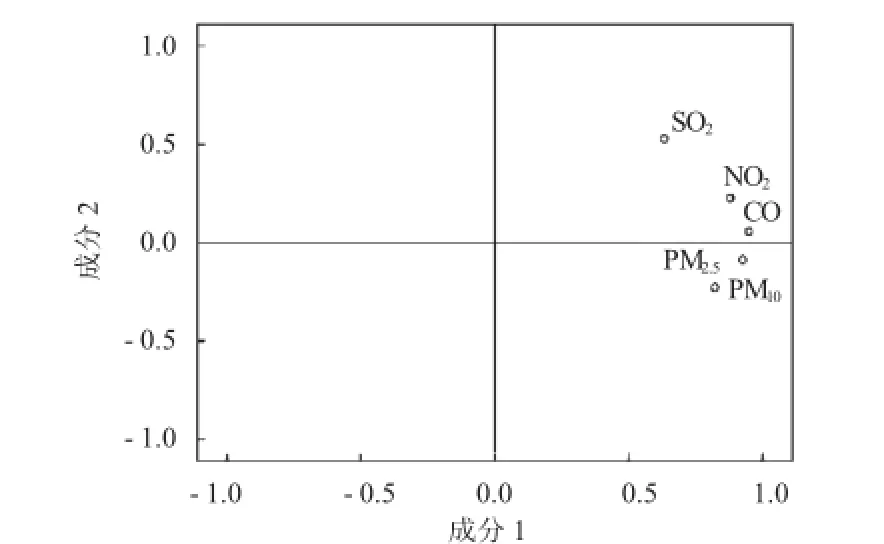
图3　主成分分析因子分解图

取前2个主成分，累计总方差为78.5%，图3显示了5个指标的因子分解结果，可以得到如下结论：

1） PM2.5和CO、SO2、NO2、PM10呈正相关性，其中CO对PM2.5的影响最大，可见CO与PM2.5几乎会同时出现。

2） PM10对PM2.5也起到正相关作用，与其他正相关因素相比，PM10与PM2.5的关系在第二主成分上相同。

3　　结论

建立了PM2.5和PM10、CO、NO2、SO2之间的线性回归模型。通过主成分分析方法揭示了不同来源对PM2.5的影响，PM10、CO、NO2、SO2和PM2.5呈正相关性。PM10和PM2.5的粒径虽然不同，但二者密切相关，减少PM10的产生有助于降低PM2.5的浓度。

［1］ Chan C K，Yao X.Air pollution in mega cities in China［J］.Atmos Environ，2008，42（1）：1-42.

［2］ 贺克斌，杨复沫，段凤魁，等.大气颗粒物与区域复合污染［M］.北京：科学出版社，2011.

［3］ 薛文博，付飞，王金男，等.中国PM2.5跨区域传输特征数值模拟研究［J］.中国环境科学，2014，34（6）：1361-1368.

［4］ 刘辉，贺克斌，马永亮，等.2008年奥运前后北京城郊PM2.5及其水溶性离子变化特征［J］.环境科学学报，2011，31（1）：177-185.

［5］ 孟昭阳，张怀德，蒋晓明，等.太原冬季PM2.5中有机碳和元素碳的变化特征［J］.应用气象学报，2007，18（4）：524-531.

［6］ 中国环境监测总站.大连空气质量指数AQI PM2.5历史数据［R］.2014-10—2015-03.

Influence Factor Analysis of Inhale Particle PM2.5

Zhu Jixiang，Xu Ran，Zhang Lin，Liu Lijun
（School of Science，Dalian Nationalities University，DalianLiaoning116600）

Four influence factors of PM2.5were obtained by using correlation analysis.The linear regression equation among PM2.5，PM10，CO，NO2and SO2was acquired by the approach of multivariate linear regression.Factor analysis was carried out through principalcomponent analysis.Resultsshowed that PM2.5waspositivelycorrelated with PM10，CO，SO2and NO2.

PM2.5；factor analysis；correlation analysis

X513

A

1005-8206（2016）01-0059-03

朱吉祥（1993—），学士，主要从事数学建模方法研究。

大学生创新创业训练计划项目（201412026030）

2015-06-02