基于卡尔曼滤波-SVR时刻峰值的短期负荷预测

沈渊彬，刘庆珍

(福州大学电气工程与自动化学院，福建　福州　350108)



基于卡尔曼滤波-SVR时刻峰值的短期负荷预测

沈渊彬，刘庆珍

(福州大学电气工程与自动化学院，福建福州350108)

以提高短期负荷预测中的时刻峰值精度为目标。为了给电力调度部门提供各时刻负荷分配的极限值，以一天中24个时刻的负荷峰值代替一天96点的负荷作为研究对象，并且在支持向量机的回归拟合(SVR)基本算法基础上，提出了一种SVR预测值经过累积式自回归—移动平均模型(ARIMA)的卡尔曼滤波调整的短期负荷预测模型。该模型利用ARIMA模型建立卡尔曼滤波方程；并将SVR预测值作为观测值，通过卡尔曼滤波的递推方程组，求得最终的负荷预测值，从而实现卡尔曼滤波-SVR预测。经过实例验证该模型可以有效提高短期负荷预测的精度。

时刻负荷峰值；短期负荷预测；ARIMA；SVR；卡尔曼滤波

1　引言

电力系统短期负荷乃至超短期负荷预测在现代智能电网的发展中发挥着极为重要的作用。但是，在电网加速建设的今天，每天中各个时候的负荷变化越加复杂和难以确定，使得通过历史负荷数据预测未来值难度也随之提高。以往在短期负荷预测中总是将一天的负荷以96点采样为基准，而考虑到现在电网在电动汽车，光电并网等新事物的接入使得负荷变化更具有不确定性的影响，导致了用历史负荷数据来预测未来值的可靠性较为难以判断。为此，本文选用在负荷变化预测中较为稳定和可靠的负荷时刻峰值为研究对象，通过对未来时刻峰值的负荷预测，为调度部门在每天各个时刻的负荷分配上提供一个可参考的负荷极限值。

同时在预测方法上考虑到在现有已经提出和被应用的短期负荷预测技术[1-2]，例如负荷趋势外推技术，回归模型预测技术，时间序列预测技术以及神经网络算法、支持向量机等，这些单一方式的负荷预测精度不是很高。所以，本文以某城市一个典型变电站的电力负荷数据为研究背景，通过文献[7]在风速预测应用中提出的一种ARMA与神经网络的混合预测模型为思路，利用对传统的支持向量机回归拟合(SVR)算法进行改进，提出一种SVR、卡尔曼滤波算法以及累积式自回归—移动平均模型(ARIMA)相结合的短期负荷预测模型。通过验证后，证明所提出的研究策略，既用较高实用价值又能提高短期负荷预测精度。

2　传统SVR与卡尔曼滤波算法原理

2.1支持向量机回归拟合数学原理(SVR)

SVR是在支持向量机(SVM)分类基础上加入ε不敏感损失函数得到[3]。SVM在回归拟合分析时，依靠一个非线性函数的映射变换到高维特征空间，在高维特征空间中寻找一个最优分界面，使得所用训练样本到该分界面的误差最小。

对于训练样本对，SVR的高维特征空间的线性回归估计函数为:

f(x)=wφ(x)+b

(1)

式中：Φ(x)是非线性映射函数；w是权重量；b是位移偏置。

当f(x)估计函数添加不敏感损失函数ε：

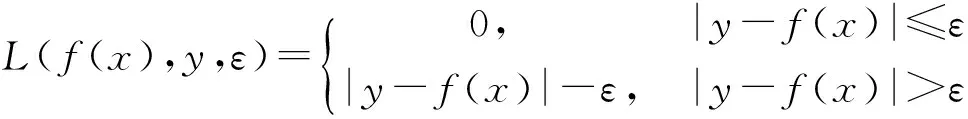
(2)

其中，f(x)为返回的预测值；y为对应的真值。当f(x)与y之间的差小于等于ε时，损失为0。

(3)

式中C为惩罚因子，ε规定回归函数的误差要求。为求解(3)式需要引入Largrange函数，并将其转化为对偶形式，从而得到最优解。于是，回归函数为：

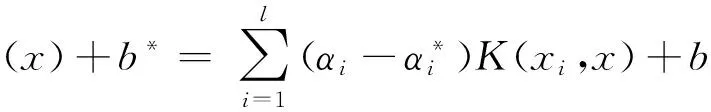
(4)

式中K(xi,x)为核函数。从而目标函数f(x)可以根据式(4)进行预测。

2.2卡尔曼滤波数学原理

卡尔曼滤波即状态空间法。它依靠状态方程递推和线性无偏最小均方差估计原则，为状态变量做出最优估计。其状态方程和量测方程如下[8]：

(5)

式中：X(t)是t时刻的状态变量；A是状态转移矩阵；Γ是激励转移矩阵；Z(t)是t时刻的观测变量；H是观测状态矩阵；w(t)是过程噪声向量；v(t)是测量噪声向量；假设w(t)和v(t)为高斯白噪声，它们的协方差矩阵用Q和R来表示，则卡尔曼滤波递推公式为：

(6)

其中：X(t|t-1)是在t-1时刻下对t时刻的状态估计；P(t|t-1)是t-1时刻到t时刻的误差协方差阵；Kg(t)是最好的卡尔曼增益；X(t|t)是系统在t时刻的最优状态估计；P(t|t)是更新的估计协方差矩阵；I是单位阵。

3　基于ARIMA的卡尔曼滤波改进的SVR模型

ARIMA的卡尔曼滤波改进的SVR模型的方法流程图如图1所示。

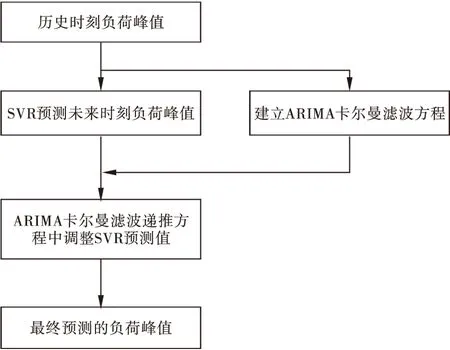
图1　改进SVR负荷预测模型

从流程图可以看出，通过SVR得到的负荷预测值作为ARIMA卡尔曼滤波的观测值，在卡尔曼滤波的递推方程中进行调整，将调整后的值作为最终的负荷预测值。这过程主要是利用了卡尔曼滤波的实时性，从而能进一步提高负荷的预测精度。

在构造卡尔曼滤波的过程中，引入了ARIMA模型。通过ARIMA对历史负荷值的拟合，求得每个时刻ARIMA模型的参数和滞后阶数，根据所得ARIMA模型参数和滞后阶数建立卡尔曼滤波方程。

在建立ARIMA的卡尔曼滤波状态转移矩阵过程中，对一天中的24个时刻负荷峰值进行分析，每一个时刻单独建立一个模型。设每天各个时刻的负荷序列为{xdt}，则ARIMA模型为：

φ(q-1)xdt=θ(q-1)at

(7)

其中：

φ(q-1)=1-φ1q-1-……-φpq-p

θ(q-1)=1-θ1q-1-……-θqq-q

(8)

{xdt}为短期负荷向量；at为随机干扰项；φi(i=1,2,…,p)和θi(i=1,2,…,q)为所建立模型的待估计参数，q-p和q-q为p阶滞后因子和q阶滞后因子，d为待预测日，t为待预测日对应的时刻。

如式(7)所示，当θ(q-1)=1时，φ(q-1)xdt=at，即AR(p)模型。根据AR模型得到如下关系：

xt(d)=φ1xt(d-1)+φ2xt(d-2)+……+φpxt(d-p)+at

(9)

令d=d+1，则上式变为：

xt(d+1)=φ1xt(d)+φ2xt(d-1)+……+φpxt(d-p+1)+at

(10)

再令：

xt(d)=x1t(d),xt(d-1)=x2t(d),……,x(d-p+1)=xpt(d);

得：

xt(d+1)=φ1x1t(d)+φ2x2t(d)+……+φpxpt(d)+at

(11)

因为

x2t(d+1)=x1t(d),x3t(d+1)=x2t(d),……,xpt(d+1)=x(p-1)t(d)

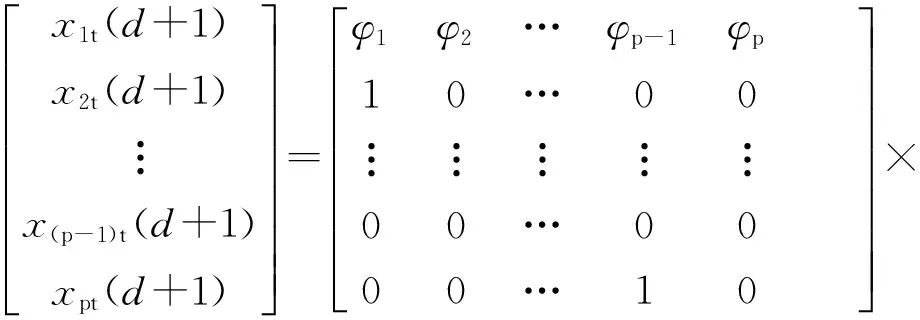
(12)

于是，得到卡尔曼滤波的状态转移矩阵为：

(13)

同时设观测方程为：

(14)

其中：wt为高斯白噪声，vt为观测噪声。

4　时刻峰值短期负荷的预测仿真实例

4.1样本数据处理

通过选取某市某个变电站2014年10月1日到2014年11月12日中每天24个时刻的负荷峰值、日期信息、气象数据作为训练样本，预测11月13日中24个时刻的负荷峰值。负荷影响因素为下面几项组成：

(1)日期类型：将周一至周五作为工作日和周六、周天以及国家法定节假日作为非工作日(量化后：工作日：1.0；非工作日：0.0)；

(2)历史负荷：10月1日到11月12日中24时刻的负荷峰值(进行归一化和反归一化处理)；

(3)气温：由每日最高温度和最低温度组成；

(4)天气情况：分为晴朗，阴天，降雨(量化后：晴朗：0.0;阴天：0.5；降雨：1.0)。

考虑到负荷的变化规律和影响因素，通过输入的相空间分析，对应SVR的输入变量如表1所示。

表1　SVR输入向量

表中：w表示日期类型向量；Q表示天气情况向量；Tmax表示最高温度向量；Tmin表示最低温度向量；L表示负荷值；d表示待预测日；d-1和d-2分别表示待预测日前天和大前天。

4.2结果评价标准

针对负荷预测结果的评价指标，本文选用最大相对误差和绝对值平均相对误差为评价标准。

4.3算例仿真

针对现在电网的快速建设，以及各种负载加入电网，使得影响电力负荷变化的影响因素越来越多，各种突发事件也相对频发，所以，本文改变以前每天96点的负荷采样，改用相对稳定的时刻负荷峰值为对象，从而使得每天的负荷变化波形由图2变为图3。

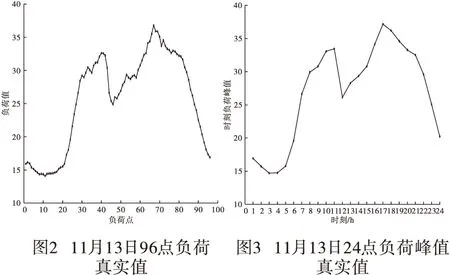
从图2和图3可见，24点的负荷峰值曲线和96点的负荷波形曲线都能按相同的趋势反映一天里的负荷变化情况。同时，针对时刻负荷峰值受突发情况影响比较小的特点，以及通过预测时刻负荷峰值可以为调度部门提供时刻负荷分配的极限值，从而更好的调整发电容量，所以，以24点时刻负荷峰值为研究对象有较大的实用价值。

在确定研究对象后，图4给出了用传统的SVR(方法1)和ARIMA卡尔曼滤波-SVR(方法2)的负荷预测情况。

图4　11月13日时刻峰值预测情况

从图4可见，方法2的时刻峰值负荷预测值比方法1更逼近真实值，特别在第10时刻和第13时刻这些日负荷极值点附近的点，方法2的预测精度明显比方法1高。

根据评价标准，表2也列出了方法2和方法1在预测中的误差值。

表2　评价标准

从表2可见，方法2在最大相对误差方面相比于方法1误差减小了2.1608%，同时在平均相对误差上也减少了1.0171%。所以，方法2明显改进了方法1的预测精度。

5　结论

本文考虑了现在电网负荷变化的偶然事件较多的情况，使得历史负荷值中可能存在特别情况下的数据，从而影响预测，同时又由于每日不同时刻的负荷峰值相对于每15分钟采样一次的96点负荷数据会相对稳定，受外界干扰相对较少，所以选用每天24点的负荷峰值作为研究对象，为电力调度部门提供待预测日每个时刻的负荷极限值作为参考，从而提前做好时刻电量的合理分配，可见这有较大的实用价值。在预测时，运用了ARIMA卡尔曼滤波对传统的SVR预测值进一步调整，从而综合利用了SVR的稳定性和卡尔曼滤波的实效性，有效提高了预测精度。所以，本文从研究对象和预测方法为负荷预测提供一种新的思路。

[1]牛东晓，曹树华，卢建昌,等.电力负荷预测技术及其应用[M].北京:中国电力出版社，2009.

[2]康重庆,夏清,刘梅.电力系统负荷预测[M].北京：中国电力出版社，2007.[3]王定成.支持向量机建模预测与控制[M].北京：气象出版社,2009.

[4]刘胜,张红梅.最优估计理论[M].北京：科学出版社,2011.

[5]王奔,冷北雪,张喜海,等.支持向量机在短期负荷预测中的应用概况[J].电力系统及其自动化学报,2011,23(4).

[6]杨国健，杨镜非，童开蒙,等.短期负荷的支持向量机的参数选择[J].电力系统及其自动化学报,2012,24(6).

[7]刘明凤,修春波.基于 ARMA 与神经网络的风速序列混合预测方法[J].2013(S1).

[8]李江,王义伟,魏超,等.卡尔曼滤波在电力系统中的应用综述[J].电力系统保护与控制,2014,42(6):135-144.

[9]Selakov,C.,Ilic,S.,Vukmirovic,S..etal.A compartive analysis of SVM and ANN based hybrid model for short term load forecasting[C].IEEE Transmission and Distribution Conference and Exposition,2012.

Short-term Peak Load Forecasting of Every Time Forecasting Based on Kalman Filtering-SVR

SHENYuan-bin,LIUQing-zhen

(College of Electrical Engineering and Automation,Fuzhou University,Fuzhou 350108,China)

Its goal is to improve accuracy in short term peak load of every time forecasting.In order to provide the load distribution limit value to power dispatch department,it uses peak load of 24 times instead of 96 points load as the research object.And it is based on SVR to propose a model which predicted value of SVR is adjusted by Kalman filtering of ARIMA.The model uses ARIMA to built Kalman filtering equation and uses the predicted value of SVR as observation values of Kalman filtering,so the value can be adjusted by recurrence equation of Kalman filtering.This is the Kalman-SVR model.The model applier to a typical example has been proved to have improved accuracy in the load forecasting.

peak load of every time;short load forecasting;ARIMA;SVR;Kalman filtering

1004-289X(2016)02-0035-04

TM71

B

2015-01-16

沈渊彬(1989-)，男，硕士研究生，研究方向为电力系统负荷预测；

刘庆珍(1971-)，女，副教授，博士研究生，研究方向为电力网络优化与设计。