基于模糊数学的两种边坡稳定性评判方法研究

沈 简 聂 彪 周 颖

(中铁西北科学研究院有限公司，甘肃 兰州 730070)



基于模糊数学的两种边坡稳定性评判方法研究

沈 简 聂 彪 周 颖

(中铁西北科学研究院有限公司，甘肃 兰州 730070)

根据35个边坡实例资料，采用模糊综合评判法和模糊聚类法进行边坡稳定性评判，并分析了两种方法的特性及适用性，指出模糊综合评判法可操作性与主观性较强，模糊聚类法更为客观。

边坡工程，稳定性，模糊综合评判，模糊聚类

0 引言

基于模糊数学的边坡稳定性评判方法能综合考虑多个因素对边坡稳定性的影响、解决各因素内部级别界限模糊不清的问题，因而得到了广泛应用，具体涉及到的方法有模糊集[1]、模糊综合评判[2,3]、模糊聚类[4]、模糊模式识别[5]等。相较于数值方法而言，模糊数学方法可以更加快速地得出边坡稳定性现状及发展趋势，对其稳定性进行分级，为工程决策提供依据。当需评判的边坡数量较多时，模糊数学方法快速分级的优势就更加明显。

在以上方法中，模糊综合评判和模糊聚类在实际工程中较为常见，诸多学者对两种模型展开了研究。这些研究主要为权重确定方法的改进[6,7]及将模型应用于不同的工况[8,9]，而两种方法何者更具优越性，在实际工程中更为适用，相关的对比研究较少。这是因为针对单个待评估边坡，两种方法得出的都是定性或半定量结论，如模糊综合评判是评判边坡有多大隶属度隶属于某种稳定级别，模糊聚类是分析边坡与已知稳定级别的边坡例有多大相似度，隶属度和相似度很难进行直观对比。

因此，本文采用两种模型对多个边坡实例进行计算，比较两种模型在对多个边坡进行稳定性评判时的准确率；依据稳定性分级标准，将评判结果按误判程度分为四类，比较两种方法的误判度；并结合工程实例分析两种方法本身的建模关键和在实际工程中的可操作性。从准确率、误判度、建模关键及可操作性这四个方面对两种方法进行对比研究，评价何者更具优越性。

1 模型原理及工程实例计算

1.1 模糊综合评判

采用已调查的贵州省境内镇水、贵新、贵毕、崇遵、三凯五条主干高速公路沿线的35个堆积层边坡实例[10]进行模糊综合评判，见表1。其中，F1指坡度，F2指坡高，F3指内摩擦角，F4指粘聚力，F5指不良地质因素，F6指地下水，F7指年降雨量，F8指人为因素，K指稳定性系数，A1～A35为边坡编号。

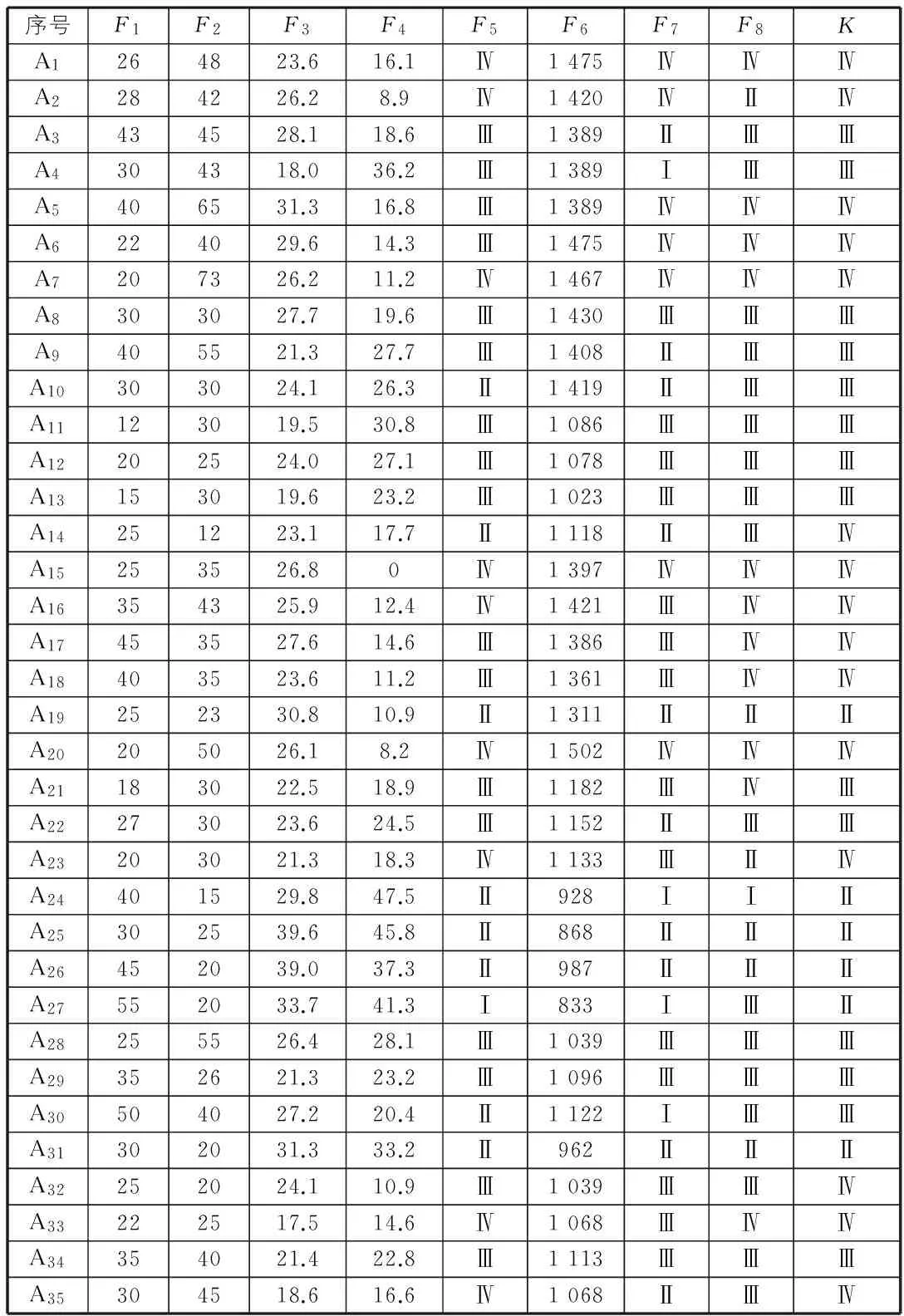
表1 边坡实例

边坡描述因子的选取非常重要，合理地选取因子才能正确描述边坡状态。黄飘等[2]统计了模糊综合评价在边坡中应用时使用因素的频率，发现坡角、坡高、降水、内摩擦角、粘聚力、地震、地下水是广泛使用的评价因子，因此本文中的因子集基本合理。

划分评判集：V={稳定(Ⅰ级)，基本稳定(Ⅱ级)，欠稳定(Ⅲ级)，不稳定(Ⅳ级)}。结合实际数据，根据已有研究成果，将各评价指标进行分级，见表2。

表2 稳定性分级标准及评判因子

将边坡因子集U按照属性类别划分成3个子集，分别为地形地貌、岩土性质及地质作用和其他因素，从而构建了二级模糊综合评判模型。即将F1,F2归为地形地貌(E1)，将F3,F4,F5,F6归为岩土性质及地质作用(E2)，将F7,F8归为其他作用(E3)。

采用AHP层次分析法[11]对主控因素的权重进行试算，其中特征根及特征向量采用和法计算。由于AHP层次分析法具有一定的主观性，因此结合前10个算例的实际情况对权重层次进行反演，用主客观相结合的方法确定权重，计算结果见表3。

表3 主控因素权值

先对每一个子集Ui进行一级模糊综合评判，以第一个子集岩体特征U1为例，其评判矩阵R1为：

其中，rij表示子集U1的第i个因子对于第j个评判等级的隶属度。U1上的权重分配A1=(a11,a12),可得U1的第一级模糊综合评判为：

B1=A1∘R1。

同理可得岩土性质及地质作用和环境因素的一级模糊综合评判结果B2和B3，即得到U的评判矩阵B=[bij]3×4，bij表示U的第i个子集对于第j个评判等级的隶属度。U上的权重分配A=(a1,a2,a3)，则第二级模糊综合评判为：

C=A∘B。

最后根据最大隶属原则，确定边坡稳定性等级。

因子隶属度的描述是模糊综合评判的关键，主控因素分为连续型变量和离散型变量。连续型因素通过建立隶属函数的方法确定隶属度，参考孙杰等[12]的研究成果及相关学者[7,8]的使用经验，采用“降半梯形”分布确定连续型因素的隶属函数，s1，s4分别对应表1中连续型变量等级评定中的两个极值，s2，s3为两个极值间的三分点。

离散型因素则采用专家评分法确定其隶属度，见表4。

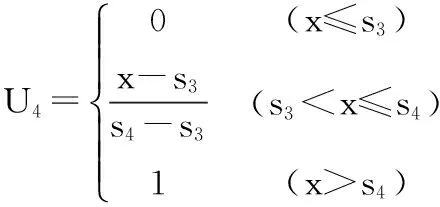
模糊综合评判计算结果：稳定边坡3个，基本稳定边坡5个，欠稳定边坡14个，不稳定边坡13个。计算结果与实际情况相符的边坡为30个，轻微误判边坡3个，重大误判边坡2个。由于篇幅限制，表5列出前4组边坡、3组轻微误判边坡及2组重大误判边坡的计算结果。

1.2 模糊聚类

有35个待分类的边坡，每个边坡都由8个因子描述其状态，可得到原始矩阵为：

其中，xij表示第i个边坡的第j个因子。各因子具有不同的数量级和量纲，直接使用，会降低甚至排斥数据的特性，所以应对其进行标准化处理。可用平移标准差变换、平移极差变换对数据进行标准化处理。

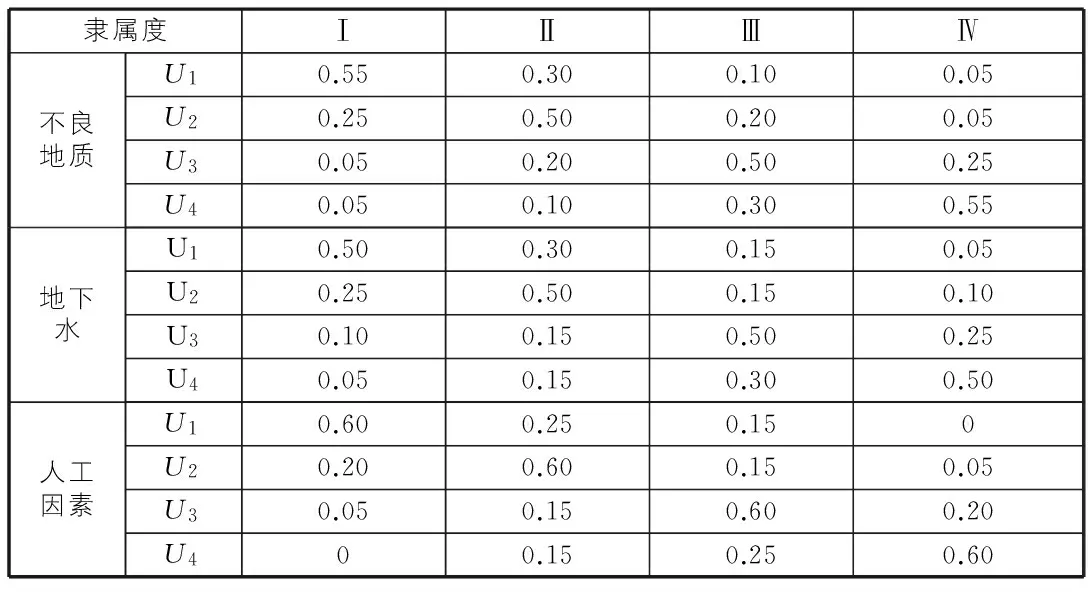
表4 离散型因素隶属度取值

表5 计算结果

离散型变量无法直接进行标准化处理，一些学者在采用模糊聚类分析边坡稳定性时回避了这类因子。这会造成分析因素覆盖不全，降低聚类结果的可靠性，因此笔者采用评分法将离散型变量转化为连续型变量，因子作用影响程度对应10分～100分。本文采用平移极差变换，方法如下：

用数rij来刻画各对象之间的相似程度，组成模糊关系矩阵R=(rij)35×35，本文采用夹角余弦法来构建R：

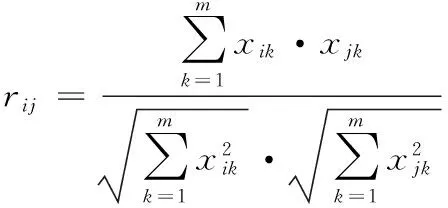
计算R2，看其是否满足R∘R⊆R，即是否具有自反性、对称性和传递性。如此反复，直到满足条件，得到模糊等价矩阵R′。选定阀值λ∈(0,1)，进行聚类。聚类原则为：Xi与Xj在λ水平上属于同类，即当rij≥λ时，Xi与Xj归为一类。通过已知边坡Xi即可确定未知边坡Xj的稳定性等级。利用MATLAB软件完成以上计算，并生成聚类图(见图1)。

结合实际需要，参考F统计量法[13]的计算结果确定λ的合理值，最终选定阀值λ=0.952，将35个边坡分为11类。

一般是将已知边坡与未知边坡混合在一起进行聚类，聚类模式的稳定级别由归类到该模式的已知边坡决定。本文为方便比较，默认所有边坡例为已知边坡，聚类模式的稳定级别由聚类图中的居中边坡决定，但单个边坡自成一类的情况视为该边坡无法识别。

模糊聚类计算结果：基本稳定边坡4个，欠稳定边坡5个，不稳定边坡20个。计算结果与实际情况相符的边坡为21个，轻微误判边坡8个，重大误判边坡0个，无法识别边坡6个(见表6)。

2 评判方法对比及模型改进

2.1 计算结果对比

计算结果分为四类：准确判断，计算结果与实际情况相符；轻微误判，计算结果与实际稳定级别相差一个等级；重大误判，计算结果与实际稳定级别相差两个等级；无法识别。两种模型计算结果具体分布如图2所示，计算结果分析如下：

1)对比计算结果的准确率，模糊综合评判法的准确率为85.7%，模糊聚类法为60.0%，前者的准确率更高。

2)对比两种模型的误判率及误判程度，模糊综合评判法重大误判率为5.7%，轻微误判率为8.6%；模糊聚类法无重大误判率，轻微误判率为22.9%。模糊聚类法误判率较高，但误判程度更低。

3)模糊聚类法的无法识别率较高，为17.1%。这是因为边坡例来自五个地域，某些边坡的数据差异性较大，找不到相似样本。这也说明了模糊聚类法的分析结果比较依赖已知边坡例。

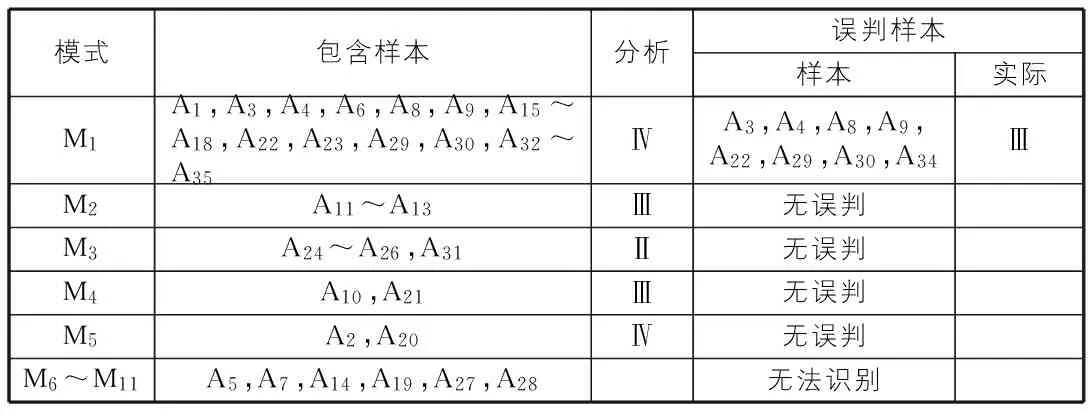
表6 聚类结果

2.2 模型对比

模糊综合评判的建模关键有两点：因子隶属度和权重的确定。目前绝大多数学者都是凭借自己的认识、经验借鉴或套用已有的隶属函数。主流的权重确定方法为专家评测法及层次分析法两种主观方法，而一些如熵值法等的客观方法没有考虑因子对边坡稳定性的影响所作的贡献，脱离了问题的本身。模糊聚类法的关键在于λ值的选取。笔者经计算发现：λ值偏大，可以有效提高计算结果的准确率，但聚类效果太差。如本文中若选取λ=0.958 6，轻微误判率将从22.9%下降到11.4%，但边坡例将分为18类，无法识别率将升至25.7%。因此，λ的选取不仅要参照F值，也要考虑聚类效果。

由2.1及2.2的实例计算可知，模糊综合评判法可直接用于单个或大量边坡的稳定性评判。但模糊聚类法无法对单个边坡或大量未知边坡直接进行稳定性分析，它还需要一定量的已知边坡例，去计算待评估边坡与已知边坡的相似度来评判边坡稳定性。经以上分析可得：

1)对比建模关键，模糊综合评判法比较依赖使用者的经验和专家意见，主观性较强。模糊聚类法则更为客观。

2)模糊聚类法需要一定量的已知边坡例才能分析待评估边坡的稳定性，模糊综合评判法则可直接建模使用，在实际工程中的可操作性更强。

综上，模糊综合评判法虽然主观性较强，但其评判结果的准确率远高于模糊聚类法。模糊综合评判法会产生低概率的重大误判，但其在实际工程中的可操作性要优于模糊聚类法。因此，模糊综合评判法更具优越性。

3 结语

1)对多个边坡进行稳定性评判，模糊综合评判法的准确率高于模糊聚类法，但会出现低概率的重大误判。模糊聚类法的误判率高于模糊综合评判法，但误判程度较低。

2)模糊综合评判法比较依赖使用者的经验和专家意见，主观性较强。模糊聚类法的关键在于阀值λ的选取，更为客观。

3)模糊聚类法需要一定的已知边坡例才能应用于实际工程，模糊综合评判法则可直接用于单个或多个边坡的稳定性评判，实际可操作性更强。

[1] 王艳霞.模糊数学在边坡稳定性分析中的应用[J].岩土力学，2010，31(9)：3000-3003.

[2] 黄 飘，谢晓锋，李 延.边坡岩体稳定性的模糊综合评判方法综述[A].第十一次全国岩石力学与工程学术大会论文集[C].北京：中国电力出版社，2010：235-241.

[3] 沈 简,饶 军,傅旭东.基于模糊综合评价法的泥石流风险评价[J].灾害学,2016,31(2):171-175.

[4] 许传华，朱绳武，房定旺.边坡稳定性的ISODATA模糊聚类分析[J].金属矿山，2000(12)：24-26.

[5] 薛凯喜，刘东燕，赵宝云，等.岩质边坡稳定性分析的模糊模式识别方法研究及应用[J].地球与环境，2011，39(1)：76-79.

[6] 刘 杰，李建林，胡海浪，等.基于有限元分析的岩质边坡稳定性模糊评判方法研究[J].岩土工程学报，2007，26(S1)：3438-3445.

[7] 沈世伟，伲 磊，徐 燕.不同权重条件下降雨对边坡稳定性影响的二级模糊综合评判[J].吉林大学学报(地球科学版)，2012，42(3)：777-784.

[8] 王勇慧，李红旭，盛 谦，等.基于模糊综合评判的公路岩质边坡稳定性分级研究[J].岩土力学，2010，31(10)：3051-3056.

[9] 朱先锋.昔格达地层开挖边坡稳定性模糊聚类分析[J].铁道勘测与设计，2006，36(5)：29-34.

[10] 周 宁，傅鹤林，袁 勇.基于模糊神经网络的边坡稳定性评价方法[J].地下空间与工程学报，2009，5(S2)：1826-1832.

[11] 郭金玉，张忠彬，孙庆云.层次分析法的研究与应用[J].中国安全科学学报，2008，18(5):148-153.

[12] 孙 杰，牟在根，张 晓.基于隶属函数选取的岩土工程模糊可靠度分析[J].岩土工程技术，2006，20(4)：200-203.

[13] 谢季坚，刘承平.模糊数学方法及其应用[M].第2版.武汉：华中科技大学出版社，2000.

Study on two evaluation methods of slope stability based on fuzzy theory

Shen Jian Nie Biao Zhou Ying

(NorthwestResearchInstituteCo.,LtdofCREC,Lanzhou730070,China)

According to 35 slopes cases, the paper applies FCE and fuzzy clustering method for slope stability evaluation, analyzes their characteristics and application scope, and finally points out that: FCE has advantages of operability and strong subjectivity, while fuzzy clustering method is more objective.

slope engineering, stability, Fuzzy Comprehensive Evaluation(FCE), fuzzy clustering

1009-6825(2016)27-0092-04

2016-07-13

沈 简(1991- )，男，硕士，助理工程师

TU473

A