基于非线性失稳准则的边坡稳定性分析

张 晋 斌

(山西晋城无烟煤矿业集团有限责任公司寺河矿,山西 晋城 048000)



基于非线性失稳准则的边坡稳定性分析

张 晋 斌

(山西晋城无烟煤矿业集团有限责任公司寺河矿,山西 晋城 048000)

运用基于塑性上界定理的非线性屈服准则，推导得出了平面应变条件下边坡稳定性系数的上界，并根据线性M-C失稳准则，提出了“广义切线”技术的改进方法，使用该方法对两个典型的边坡稳定性问题进行了分析，获得的上限解与垂直开挖边坡的下限解相等。

边坡，土体，极限分析，非线性分析

0 引言

对于岩土工程师来说，边坡稳定性的测定是一个非常重要的课题。许多研究人员试图开发和精心设计边坡稳定性评价方法。在过去，提出的稳定性分析方法可分为以下四类：1)包括条分法在内的传统极限平衡方法；2)特征线法；3)包括上、下界方法的极限分析法；4)有限元或有限差分数值技术。边坡稳定性的极限分析方法已经被许多研究者所应用，通过虚功原理，如果所有外荷载所做的虚功等于符合约束条件的系统虚位移导致的内能耗散，那么系统刚性条块(或楔形体)处于平衡状态。上界定理是建立在虚功原理基础上的，假设一个遵循关联流动法则的完全塑性土体模型，它规定任何机动位移速度场的内能消散可等效为外载荷所做的功，因此，可以推导出实际安全系数或稳定系数严格的上限，这个上界满足力的平衡且不需要对条间力进行假设。

目前，线性MC失稳判据常用于稳定性问题的极限分析。原因可能在于线性MC失稳判据可表示成圆形。这一特点使得滑动面近似为圆形成为可能，这是在应力空间中平面应变问题的一个线性应力函数。因此，基于上、下限定理，稳定性和承载力问题的解析是线性规划问题。运用线性MC失稳判据，Lymser(1970)，斯隆(1989)，斯隆和Kleeman(1995)，金姆等(1999，2002)采用有限元法和线性规划法解决了稳定性和承载力问题。此外，对于平面应变问题，冯·米塞斯和线性MC失稳准则主应力空间中的屈服面具有线性特征。这个属性使得精确预测岩土结构如浅基础和边坡稳定问题的失稳机理成为可能。一般来说，经典假设失稳机制中，冯·米塞斯失稳准则假设为平面或圆形，而线性MC失稳判据(陈，1975)则假设为平面或对数曲线。

本文使用“广义切线”技术提出一种改进的方法。该方法并非采用实际的非线性失稳准则，而是采用切线(线性MC失稳准则)形式表达功和能量耗散。本文将陈(1975)的线性失稳准则进行边坡稳定性分析工作，延伸到了使用非线性失稳判据。

1 非线性失稳判据的上界解

本文中的方法采用陈(1975)的基本思想，也即旋转对数螺旋面。

1.1 “广义切线”技术

通过线性破裂面计算得到的极限载荷将是实际极限载荷的一个上界值(陈，1975)，它总是限定实际的非线性破坏面。这是由于这样的事实：受限定的实际非线性破裂面的强度不小于实际的破坏面。在现有的分析中，非线性失稳判据在点M处的切线。在相同的正常应力水平下，切线强度等于或超过非线性失稳判据中的强度。因此，切线所代表的线性失稳判据将给出材料实际荷载的一个上限，材料的破坏是由一个非线性失稳判据来决定的。事实上，许多研究人员(Lymser，1970；斯隆，1989；斯隆和Kleeman，1995；Yu等，1998；金姆等，1999，2002)在他们的极限分析中采用了这种方法。线性MC失稳判据可以表示为一个圆，在应力空间中平面应变条件下，它的方程是(σx-σv)2+(2τxv)2=[2ccosφ-(σx+σv)sinφ]2。在公式中，对于线性MC失稳判据，c和φ代表内聚力和内摩擦角。应当指出的是，在饱和土体中，c和φ是有效内聚力和有效摩擦角。为了使用塑性上限定理求解作为一个线性规划问题的稳定性问题，有必要由外多边形近似为圆形，它总是限定线性MC失稳判据。外多边形对应的上界解超过或等于运动学方法的线性MC失稳判据对应的上界解。

在目前的研究中，线性MC切线图表示的线性失稳准则用于极限分析，它始终与非线性失稳判据曲线相切。

1.2 额外功率和能量耗散

根据上限定理，将沿速度不连续的能量耗散率等价于外力在任何可变速度下的功率会导致稳定系数(或极限荷载)不小于或最多等于实际的稳定系数(或极限荷载)。最优上限解可通过一种优化方法获得。在目前的研究中，外力的工作效率是通过土体自重得到，由于塑性剪切，内能将因速度的不连续性而消散。由于切线(线性MC失效准则)的应用，可以采用对数螺旋线失稳机理进行上界分析。

外力(自重)的功率表示如下：

Wext=γ∫AVdA

(1)

其中，A为土体破裂面上方的横截面面积；γ为土体重度；V为对数螺旋线失稳曲线的切向量。沿不连续速度方向的内能耗散率表示如下：

Dint=∫L(τVcosφt-σnVsinφt)dL

(2)

其中，L为速度重度的时间。对于线性MC失稳条件，式(2)可以简化为如下形式：

Dint=∫LccosφVdL

(3)

它与实际的应力矢量的大小是独立的。式(3)中，c为线性MC故障判据中的土体内聚力和内摩擦角。在失稳判据为非线性情况下，式(3)无法得到，因为只有一个应力分量可以从式(2)中消除。如果非线性失稳判据中曲线的切线作为线性MC故障判据，式(3)是有效的，尽管这将产生一个实际极限载荷(或稳定性系数)的上界。为简单起见，在目前的分析中采用切线形式。

2 影响边坡稳定的因素

根据边坡破坏模式，对比式(1)中外力的功率与式(2)中内能耗散率，我们可以得到式(4)：

H=ctf(θh,θ0,φt)/γ

(4)

其中，f(θh,θ0,φt)可表示为：

{sin(θh+α)exp[(θh-θ0)tanφt]-sin(θ0+α)}

(5)

式(5)中，变量f1～f3取决于几何参数和切线角。变量f1～f3由陈(1975)给出。

通过极限分析的上界理论，式(4)给出一个关于边坡高度H的临界值。这个变量H有最小值，当满足下面这个条件时：

(6)

解出上述方程，然后将参数θh，θ0和φt代入式(2)，我们可以得到倾斜边坡的临界高度的上限值。此处，我们可以采用相继的二次设计来优化目标函数以避免解决式(6)的困难。稳定因数Ns被定义为Ns=γHc/c0被张和陈引用(1987)，也被德雷舍和克里斯托杜卢引用(1988)，用来解释具有非线性破坏准则的边坡问题。Ns是一个无量纲数，而且Ns的量级不仅仅取决于边坡角度α和β，还取决于非线性破坏准则的参数，包括m，σt和c0。

3 带有张拉裂缝的垂直土质边坡的极限分析

除了真正的水泥土外，土体通常不能承受拉力。在现场，地表水的作用和张拉裂隙都有可能破坏土的抗拉强度，土的抗拉强度不可靠，在实际应用中可以忽略不计。在下面的分析中，张拉裂纹被引入，没有能量耗散沿拉伸裂纹，能量仅沿剪切线消失，如图1所示。

4 上限稳定分析

一种平移破坏类型组成的垂直张裂缝和不连续面AB如图1所示。土体的单位重量是γ。拉伸裂纹长度是nH(0≤n≤1)。n=1意味着拉伸裂隙贯穿了整个立坡，另外，n=0意味着没有拉伸裂隙存在。临界高度是指边坡开挖后由于自身重量而坍塌的高度。我们假设破坏面是沿着在垂直方向上角度为ω的非连续面。当重力做功达到非连续面AB的功的耗散值时即达到了极限状态。重力做功等于速度的垂直分量与土楔重量的乘积，即为：

wext=0.5γH2tanω(1-n2)vcos(φt+ω)

(7)

能耗率等于速度的切向分量与AB面的长度及ct的乘积，即为：

(8)

将重力做的功与内耗散的功等同起来就得到:

(9)

式(9)是t和W的一个函数；我们可以通过将φt和ω最小化得到一个临界高度的上限。此处，采用二次解析法来优化式(9)目标函数。

对于图1的垂直切坡，要得到下限解，需要解得静力许可场的解，而该场必须满足以下的应力平衡方程:

(10)

该应力场不能违反非线性破坏准则。这意味着该应力必须处于非线性矩阵的包络线内。该三向应力系统必须满足应力平衡条件。三向应力状态被假定为一个单轴压缩状态Ⅰ，双轴压缩状态Ⅱ和三轴压缩状态Ⅲ。

为了确保该应力状态在单轴压缩状态下不能违反非线性破坏准则(1)，我们得出：

(11)

在式(11)中，有H和φt2个变量。解得这2个方程，将得出高度H。由于非连续应力场满足任何土的质量和边界条件下的应力平衡方程，而且不超过应力平衡准则，因此由式(11)解得的H为临界高度Hc的下限。

5 比较

通过采用上限方法在非破坏准则条件下得到边坡的稳定性因素Ns的计算结果。将得到的Ns的计算结果列于表1中，并与张和陈(1987年)得到的数据及Drescher和Chistopoulos(1988年)得到的数据对比。

表1中显示的稳定性因数Ns是当c0=90 kPa，σt=247.3 kPa，α=0°条件下，非线性系数m从1.2到2.5取值下的结果。

表1 不同取值条件下稳定因数比较

从表1看出，作者得到的上限解与另外两组数据几乎相同。另外，通过表1可以看出，稳定性系数Ns当c0，σt和m相同，α=0°时随着边坡角度β的增大而变小。

图1中的垂直切坡采用上限和下限方法进行分析。表2中显示的通过两个方法在c0=90 kPa，σt=247.3 kPa，α=0°和n=1的条件下得到的稳定因数Ns的值。由表2中可以看出，下限解和上限解对于垂直切坡是一样的。但是，图1中上限计算所用的速度场和下限所用的应力场的一致并不意味着速度场和应力场都是实际存在的。

表2 上限与下限计算结果比较

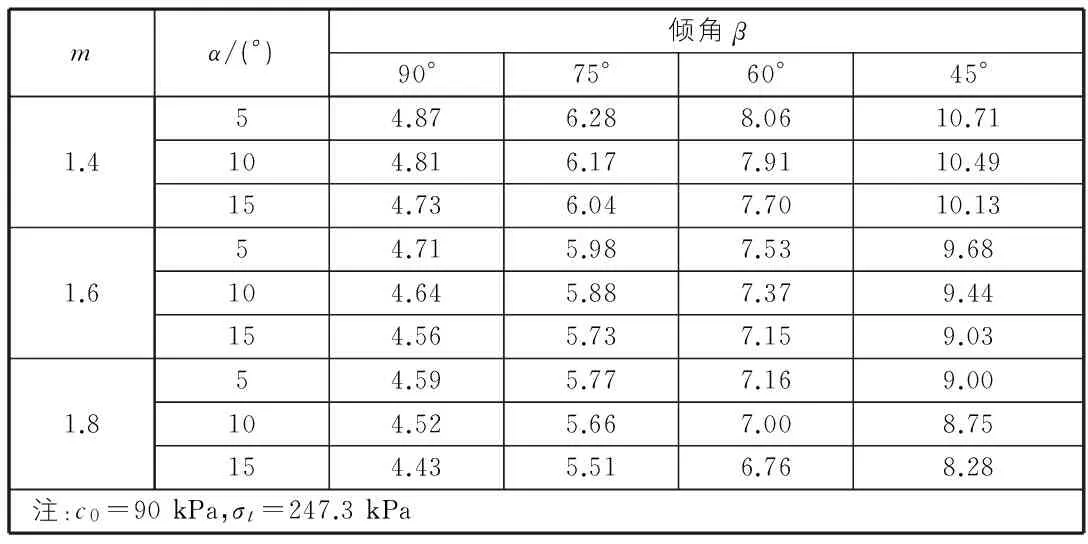
表3 α≠0°条件下稳定因数计算结果

5.1 边坡倾角α的影响

张和陈(1987)与德雷舍和赫里斯托普洛斯(1988)给出了一种在0值情况下的数值结果。在实践中，边坡倾角α可能大于0°。表3给出了稳定系数n值为σt=247.3 kPa和c0=90 kPa，用α=5°,10°和15°。从表3中可以看出，当参数m，σt，c0和β为常数时，上限解随坡度α的增大而增大。

5.2 系数m的影响

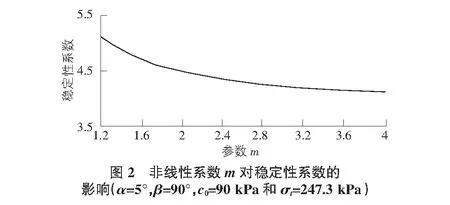
图2说明系数m在α=5°，β=90°，c0=90 kPa和σt=247.3 kPa条件下的稳定因数Ns的影响。

5.3 应力σt的影响

作者得到的稳定因数Ns的结果被展示在图3中，其中α=5°，β=90°，m=1.6，c0=90 kPa，σt从50 kPa到200 kPa。从图3可以明显看出，稳定因数随应力σt的增长而减小。

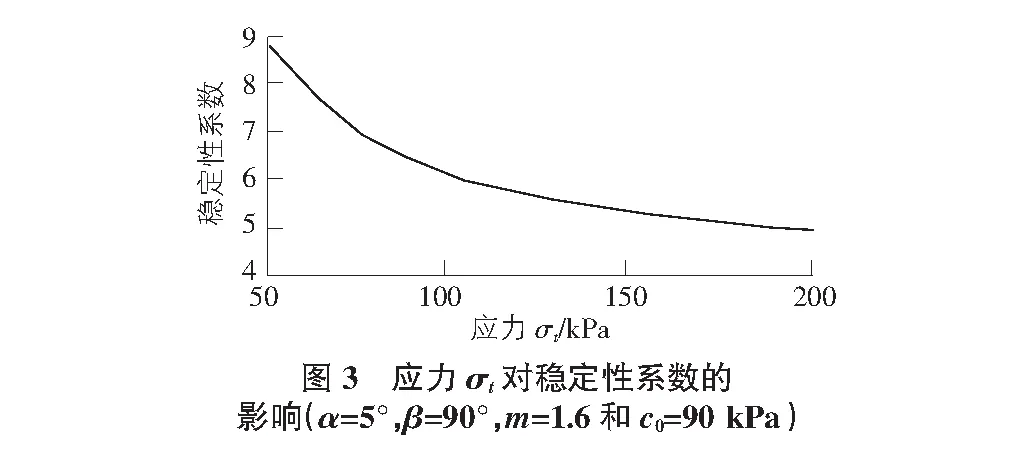
5.4 初始内聚力c0的影响

如图3所示，当α=5°，m=1.6，β=90°，σt=247.3 kPa时，可以得到边坡的c0值从40 kPa到120 kPa范围变化时的稳定因数值。如果应用线性破坏准则，那么稳定因数仅和边坡几何形态参数(α和β)和摩擦角有关，和内摩擦力无关。然而，从图4中可以看出，应用非线性破坏准则，可以得到当参数m，σt，α和β为常数时，稳定因数随着初始内聚力c0的增长而增长。

6 结语

本文采用接近非线性破坏准则的“广义切向”技术的改进方法是基于塑性力学的上限理论提出的，并用来分析边坡的稳定性。对于没有荷载的边坡，采用提出的上限方法计算的稳定因数值与张和陈(1987)及德雷舍和赫里斯托普洛斯计算的值几乎一致。对于如图1所示的垂直切坡的平移失效机理，相同的解决方式为利用目前的上限理论和下限理论得到。目前，利用非线性破坏准则的方法，边坡角度α，系数m，应力σt和初始内聚力c0的影响已经被研究和探讨，得到参数α，m，σt和c0对边坡稳定性系数有重要影响。

[1] 金,J,萨尔加多,R,于,H.S.考虑孔隙水压力的边坡极限分析[J].岩土与地质环境工程,1999,125(1):49-58.

[2] 金,J,萨尔加多,R,李,R.基于极限分析的复杂土质边坡稳定性分析[J].岩土与地质环境工程,2002,128(7):546-557.

[3] 米恰洛夫斯基,R.L.均质边坡稳定性图表[J].岩土与地质环境工程,2002,128(4):351-355.

The slope stability analysis based on nonlinear instability criterion

Zhang Jinbin

(SiheCoal,ShanxiJinchengAnthraciteCoalMiningGroupLimitedLiabilityCompany,Jincheng048000,China)

Using the nonlinear yield criterion based on plastic upper bound theorem, this paper derived the upper bound of slope stability coefficient under plane strain condition, and according to linear M-C instability criterion, proposed the improvement method of “generalized tangent” technology, analyzed two typical slope stability problems using this method, gained the lower limit solution equal of upper bound solution and vertical excavation slope.

slope, soil, limit analysis, nonlinear analysis

1009-6825(2016)27-0078-04

2016-07-13

张晋斌(1972- )，男，工程师

TU413.62

A