四旋翼飞行器

王智敏，王欢欢，崔敬魁，李东达

（西安理工大学自动化与信息工程学院，陕西 西安 710048）

四旋翼飞行器

王智敏，王欢欢，崔敬魁，李东达

（西安理工大学自动化与信息工程学院，陕西 西安 710048）

四旋翼飞行器属于多旋翼直升机，能垂直起降，无需滑翔跑道，具有良好的机动性，在许多领域都有重要的应用价值。因此，我们设计并搭建四旋翼飞行器软硬件平台，主要包括了嵌入式四旋翼飞行器飞行控制板，四旋翼飞行器地面站和上位机三部分。通过分析飞行动力系统数学模型，惯性导航技术和进行四元数梯度下降滤波器的姿态解算，设计四旋翼飞行器串级PID姿态控制器，并对高度进行频域矫正控制，主要实现了四旋翼飞行器的手控模式飞行和一键起飞与降落的自主定高模式飞行；同时具有低电压报警、并通过上位机实时监测飞行器状态等功能。

四旋翼飞行器；自主起降；姿态解算；姿态控制

编者按：2015年9月20日，首届“萨驰杯”智能科技创新大赛决赛在苏州大学敬贤堂成功举办。大赛由萨驰华辰机械（苏州）有限公司主办，中国石油和化工勘察设计协会橡胶塑料设计专业委员会、中国橡胶工业协会机械模具分会、《橡塑技术与装备》杂志社、上海交通大学机械与动力工程学院、哈尔滨工业大学机电工程学院、东南大学机电工程学院、苏州大学机电工程学院、青岛科技大学、西门子工厂自动化工程有限公司及罗克韦尔自动化（中国）有限公司共同协办。

为共同促进我国科技教育多元化，实现中国制造2025的中长期目标提供有力的支持，促进企业文化活跃橡塑行业科技文化事业发展。本刊将分期连续选登参赛作品，以供业内人士全方位、宽领域了解科技发展动态。

四旋翼飞行器属多输入多输出的非线性、欠驱动模型，其输入为四个电机的转速，输出为六自由度飞行器运动状态（三个自由度姿态，三个自由度位置），故各控制量直接必然存在耦合，给控制带了一定的困难，对于四旋翼飞行器常用的较为稳定的控制算法有滑模控制、反步法、PID控制等。

小型无人机在军事、医疗、电力，农业、航拍等领域都有巨大的应用价值，对四旋翼飞行器的深入研究可推动小型无人机的推广。

1 飞行器动力学模型

1.1 四旋翼飞行器简介

1.1.1 四旋翼飞行器结构

四旋翼飞行器具有四个呈对称分布的螺旋桨，其中1，3电机和2，4电机旋转方向相反，如图1，螺旋桨下方电机固定在四个机架轴上，四个机架轴在同一水平面上，各相邻轴间夹角为90°，轴的中心连接在一起。

1.1.2 四旋翼飞行器运动状态

（1）垂直运动

当四旋翼螺旋桨产生的拉力在大于或小于飞行器重力时，飞行器做升降运动，若拉力正好等于飞行器重力时，飞行器可实现悬停，如图2所示。

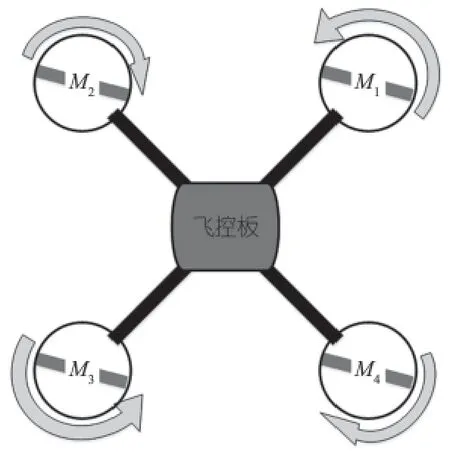
图1 四旋翼飞行器螺旋浆电机驱动示意图

图2 飞行器悬停时各螺旋浆受力示意图

（2）俯仰运动和翻滚运动

如图，当四旋翼M1，M2电机和M3，M4电机拉力保持平衡时，四旋翼在俯仰方向保持平衡，若M1，M2电机拉力大于M3，M4电机时，四旋翼做机头向上倾斜动作，反之向下。同理，四旋翼M1，M4电机拉力大于M2，M3电机时，四旋翼向左倾斜，反之向右，如图3所示。

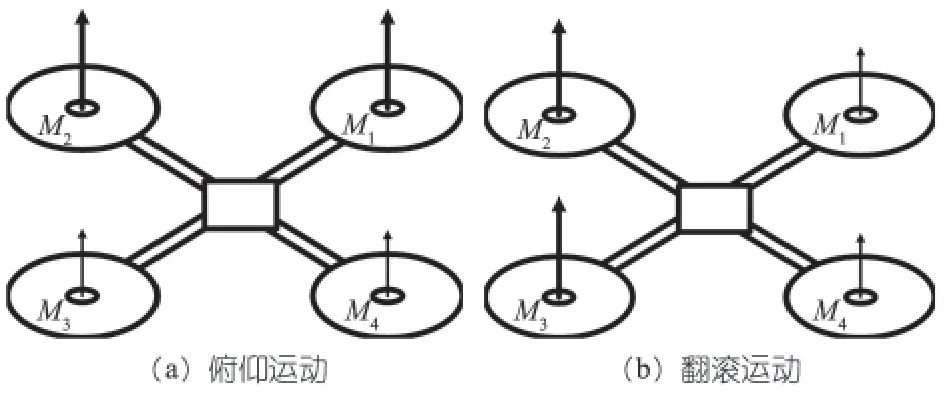
图3 飞行器俯仰、翻滚各螺旋浆受力示意图

（3）偏航运动

设四旋翼M1，M3电机顺时针旋转，M2，M4电机逆时针旋转，则在螺旋桨旋转过程中，M1，M3电机的螺旋桨对电机轴产生了逆时针方向的反扭力，M2，M4电机对电机轴产生了顺时针反方向的反扭力，由于电机固连在飞行器上，故反扭力直接作用在了四旋翼机身上，当M1，M3电机反扭力和M2，M4电机反扭力平衡时，四旋翼航向不发生变化，当M1，M3电机反扭力大于M2，M4电机时，飞行器逆时针旋转偏航，反之顺时针旋转，如图4所示。

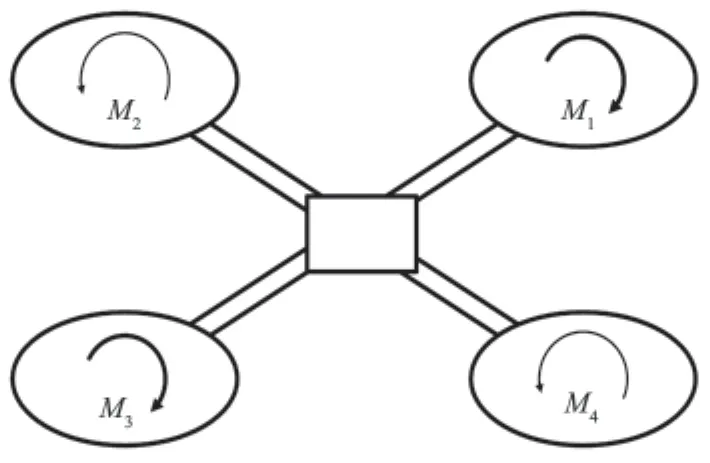
图4 飞行器旋转偏航各螺旋桨受力示意图

1.2 坐标变换矩阵

1.2.1 导航坐标系n

导航坐标系是指地球地理坐标系，通常我们以东北天坐标系作为地理地坐标系（g）方向，规定xg，yg，zg依次指向东、北、天方向。

1.2.2 机体坐标系b

机体坐标系是指与飞行器固连的坐标系，原点为飞行器重心位置，xb轴对应于飞行器右侧方向 ，yb轴对应于飞行器前方，z轴垂直于飞行器平面向上，与xb，yb轴形成右手系。

1.2.3 旋转矩阵

在飞行动力学中，通常以欧拉角来描述机体坐标系与导航坐标系之间的关系，如图5所示。

欧拉角定义如下：

图5 欧拉角描述机体坐标系与导航坐标系之间的关系

航向角Ψ——机体坐标系xb轴在水平面上投影与地面坐标系xg轴（在水平面上，指向目标为正）之间的夹角。

俯仰角θ——机体坐标系X轴与水平面的夹角。当X轴的正半轴位于过坐标原点的水平面之上（抬头）时，俯仰角为正，否则为负。

滚转角Φ——机体坐标系zb轴与通过机体xb轴的铅垂面间的夹角，机体向右滚为正，反之为负。

从机体坐标系到导航坐标系的姿态矩阵为：

1.3 四旋翼飞行器动力学模型

为了建立数学模型更加方便，做出如下假设：

（a）飞行器是刚体，飞行过程中其质量保持不变；

（b）将导航坐标系视为惯性坐标系，即忽略地球的自传，公转及曲率影响；

（c）导航坐标系原点与机体坐标系原点和飞行器质心重合；

（d）四旋翼飞行器受到的螺旋桨拉力和螺旋桨转速平方成正比；

（e）四旋翼飞行器在飞行过程中受到的重力和阻力保持不变，忽略空气摩擦等其他因素影响。

根据牛顿第二定律和动量矩定理有：

设Fx，Fy，Fz； p，q，r分别为、在机体坐标系下三个坐标轴x，y，z，上的分量。

1.3.1 线运动方程

机体受到的外力有重力、旋翼拉力和阻力。

重力为：G=mg

式中：

g——重力加速度；

ρ——空气密度；

Cd——旋翼阻力系数；

Ct——旋翼升力系数；

Ωi——第i个旋翼的角速度。

式（2）在机体坐标系下，有：

1.3.2 角运动方程

欧拉角的角速度与机体角速度有如下关系：

解得：

由前述假设，四旋翼重心与机体坐标系原点重合，故飞行器惯性矩阵I为对角阵：

由欧拉运动方程，可得飞行器坐标系下三个轴分量Mx、My、Mz的角运动方程为

1.3.3 模型简化

为了便于分析，在此定义四个独立通道的输入量U1、U2、U3、U4，则有如下公式：

其中U1表示油门通道输入，U2表示滚转通道输入，U3表示俯仰通道输入，U4表示航向通道输入。

忽略空气阻力，将式（10）带入式（5）得到线运动方程为：

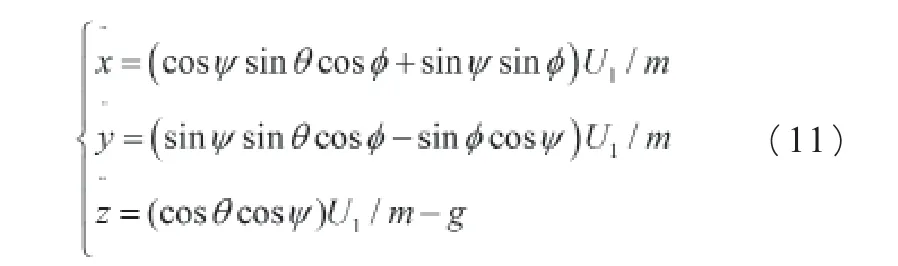
角运动方程为：

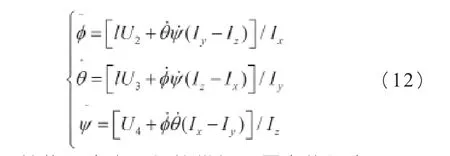
其中I为旋翼中心到机体坐标系原点的距离。

2 梯度下降法姿态滤波器

2.1 飞行器姿态的四元数表示

四元数是有四个元组成的数

中，q0，q1，q2，q3是实数，i，j，k既是互相正交的单位向量，又是虚单位

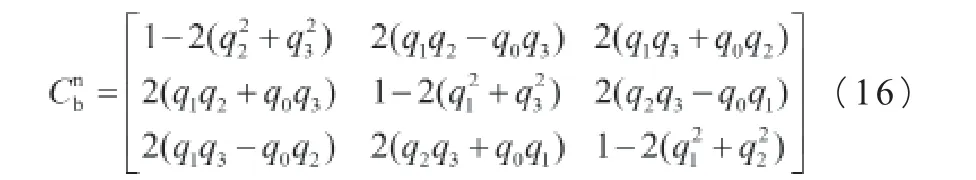
描述刚体旋转的四元数是规范化四元数，有

欧拉角旋转矩阵和四元数旋转矩阵对应关系得：

2.2 梯度下降滤波器

常用的滤波方法有互补滤波，卡尔曼滤波，扩展卡尔曼滤波等。本设计采用梯度下降法和互补滤波结合的姿态滤波器法。

四元数微分方程有

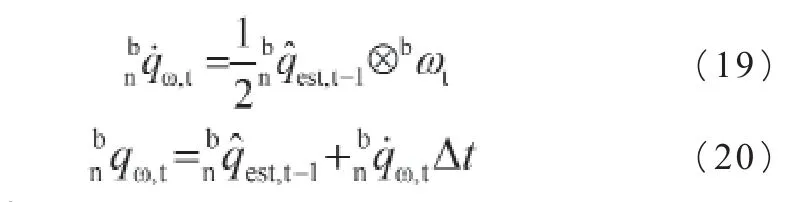
2.2.1 建立误差函数

首先根据机载惯性测量单元（三轴加速度计和三轴磁力计）的测量值与导航坐标系固连参考做差作为误差估计函数，认为在导航坐标系下加速度仅为重力加速度，通过导航坐标系到机体坐标系的变换:

对于磁力计，因为地磁场可分解到水平面和重力方向，与定义的东北天坐标系对应，认为水平分量正好与x轴方向对准，导航坐标系下磁力计只在x，z方向上存在分量。

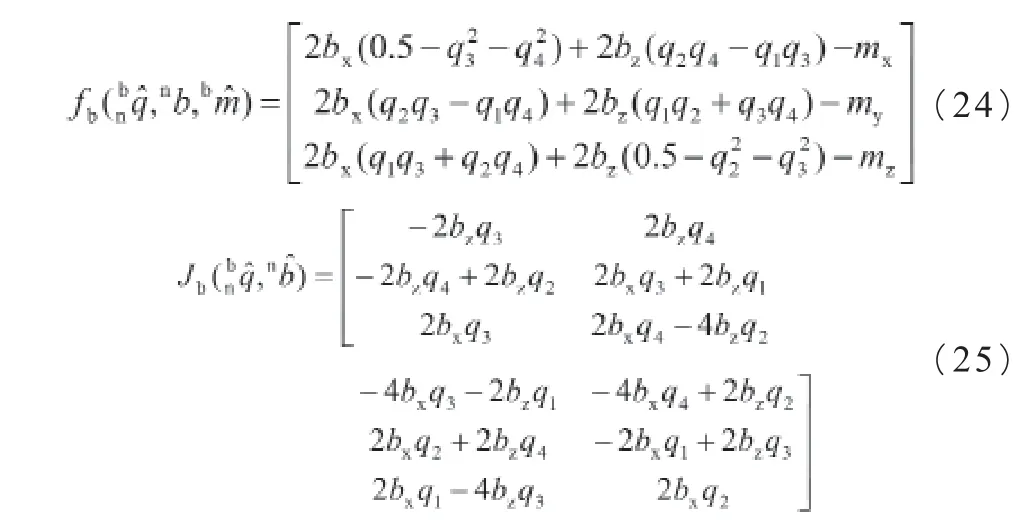
由于加速度计是基于导航坐标系重力方向校准的，无法判断航向，而磁力计可以进行航向校准，故需要两者结合作姿态校准，有：

然后计算梯度，如果仅使用加速度计，则选择下式中的第一个梯度，选择同时加速计和磁力计时选择第二个作为梯度。

2.2.2 梯度下降法迭代

梯度下降法迭代公式为：

μt为梯度下降法步长， Δt为陀螺仪采样周期，为陀螺仪测量的姿态改变速率，而α是μ对加速度计和磁力计的放大比例系数。

3 飞行控制与软件设计

上文引入的四个控制量，油门控制量U1，滚转控制量U2，俯仰控制量U3，偏航控制量U4，而其对应输出分别为螺旋桨基础转速，滚转角Φ，俯仰角θ，偏航角Ψ。这样引入控制量可以实现对欠驱动系统的解耦，实际上，此处只控制了四旋翼发姿态角，然而四旋翼飞行器的线运动受角运动的影响，如需进行线运动控制做位置闭环，可采用线运动控制作为外环，角运动控制作为内环来控制，因为角运动较线运动而已具有频带快，运动速度快的特点。

3.1 姿态控制

姿态控制采用串级PID控制，内环为角速度环，外环为角度环，从而很大程度的削弱了模型内部的非线性，取得了良好的控制效果。

为避免在特定条件下微小误差长时间累积导致积分项过大，导致系统由积分项主导的不稳定现象，本设计在PID控制器内对积分项进行了限幅，从而有效的避免了积分项过大导致系统不稳定的情况出现，如图6所示。

图 6 PID控制器内对积分项限幅框图

3.2 高度控制

高度控制采用普通频域矫正PID控制，如图7所示。

图7 普通频域矫正PID控制框图

在高度控制方面，为防止输入突变后由于微分作用引起输出的巨大变化，本设计采用微分分离的方法，有效的避免了输入突变后由于微分引起的系统震荡。同时在也在积分上做了积分限幅。

4 测试与结果分析

4.1 姿态解算效果测试

通过上位机实时观察姿态角和实际飞行器姿态角对比，可看出姿态解算精度和快速性均可满足控制要求，如图8所示。

同时通过上位机可进行PID在线调参和传感器校准，如图9所示。

4.2 飞行姿态控制效果测试

飞行过程中姿态角波形如图10所示，其纵坐标单位为角度，其中灰色线为横滚角、蓝色线为俯仰角，图示角度均是四旋翼飞行器在飞行过程中实测得到。由此可见飞行过程中姿态波动小于0.5°。

飞行效果如下图11所示。

4.3 高度闭环测试

飞行过程中高度变化如图12所示，其纵坐标单位为米，可见高度控制效果良好。

图8 由上位机实时观察对比

图9 PID在线调参和传感器校准

图10 飞行过程中姿态角波形图

5 结论

本设计对四旋翼飞行器姿态控制，高度控制和飞行原理进行了分析，并对四旋翼飞行器进行动力学建模，同时采用梯度下降法姿态滤波器进行姿态解算，并根据四旋翼飞行器简化模型设计了串级PID控制器。并通过制作四旋翼飞行机身结构和硬件电路，设计方向控制PCB板和四旋翼飞行器地面站，在四旋翼实体上进行了控制策略和算法的验证，从而证明了梯度下降法姿态滤波器和串级PID姿态控制器的可靠性。

图11 飞行照片图

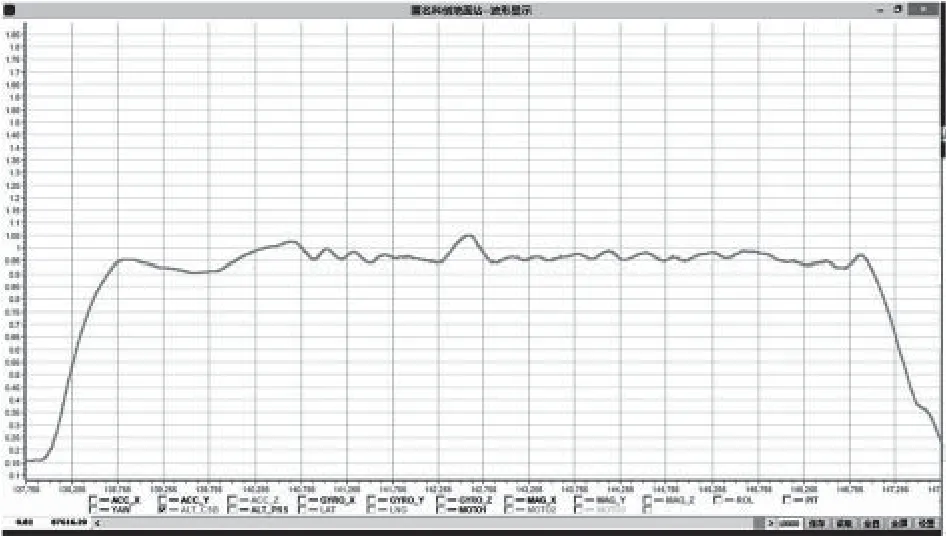
图12 飞行过程中高度变化波形图

［1]秦永元. 惯性导航［M］. 北京：科学出版社，2014：244～259.

［2]Sebastian O.H. Madgwick. Estimation of IMU and MARG orientation using a gradient descent algorithm［C］. IEEE International Conference on Rehabilitation Robotics，Switzerland，2011:1～5.

［3]STMicroelectronics.Using LSM303DLH for a tilt compensated electronic compass［Z］.2010:20～24.

［4]Memsense. Bias and Sensitivity Corrections of Magnetometers Revision 1［Z］.1～4.

（R-03）

Four-rotor aircraft

Four-rotor aircraft

Wang Zhimin, Wang Huanhuan, Cui Jingkui, Li Dongda
(School of Automation and Information Engineering, Xi'an University of Technology, Xi'an 710048, Shaanxi)

The four-rotor aircraft is a multi-rotor helicopter that can take off and land vertically without arunway glide. It has good fl exibility and important applications in many areas. Therefore, we designed and built hardware and software platforms for the four-rotor aircraft, including embedded four-rotor aircraft fl ight control panels, ground station and host computer. By analyzing the flight dynamic mathematical model, inertial navigation technology and attitude algorithm of quaternion gradient descent fi lter, we designed a cascade PID attitude controller for the four-rotor aircraft, and run frequency domain correction control for the height. They mainly achieved manual mode fl ight and autonomous height mode fl ight with one-key take-off and landing; the platform also had functions such as low voltage alarm and real-time monitoring of aircraft status through the host computer.

four-rotor aircraft; autonomous takeoff and landing; attitude algorithm; attitude control

V212.4

1009-797X（2016）02-0100-07

B

10.13520/j.cnki.rpte.2016.02.039

王智敏（1989-），女，就读于西安理工大学硕士研究生，研究方向智能机器人。

2015-10-26