电力负荷趋势外推预测算例分析与模型检验

电力负荷趋势外推预测算例分析与模型检验

电力系统负荷预测按照预测周期可以分为长期、中期、短期和超短期预测。负荷预测结果数据主要用来决定新的发电机组的安装和用于电网规划、增容和改建，当然有时也可以用于电网在线控制，通过对发电容量的合理调度，达到在满足一定的运行条件下使发电成本最小的目的，实现经济运行。经过长期的发展，电力负荷预测方法的研究出现了很多新的预测技术包括利用现代数学和人工智能的一些新方法。但这些所谓的新技术也常常存在一些问题，比如模型复杂，运算量大，需要大量的实际历史数据，优化寻优过程存在不确定性，而且人员素质要求高，要求比较高深的数学知识，在目前电网实际中实用性和适用不强。特别是在建立模型的历史数据比较少情况下，我们需要更简单实用并且精度较高的负荷预测方法，哪怕是传统方法。常用的传统方法有趋势外推法和线性回归法等。趋势外推法具有的优点包括所需历史数据少，操作简单，模型容易建立，其缺点在于，如果负荷出现变动，可能会引起较大的误差。本文采用的趋势外推法预测模块将主要采用的是线性趋势下二次指数平滑技术和二阶自适应系数法。

趋势外推法

线性趋势预测方法主要有：二次滑动平均法、二次指数平滑法及二阶自适应预测方法。这些方法都具有如下相同特点：假定历史数据xt具有线性趋势，则在t时刻利用数据序列x1，x2，…，xT给出预测值序列：为了确定求出和。需要说明的是，本文所用方法，不是像一般的只是在整个时段内拟合出一条直线，而是在每个t时刻，由预测公式动态地定出t+1时刻的预测值，从而使得T时刻之前的一些预测值不一定在这一条直线上，这与一般直线拟合（如回归方法中拟合历史数据的一条直线表示）预测是有区别的。但是，t＞T时的预测值还是由直线计算出。

趋势外推法预测基本原理与理论分析步骤

二次指数平滑技术

假设存在下列一次指数平滑序列（设其平滑系数0＜a ＜1）：

在此基础上，我们可以计算二次指数平滑序列：

对于二次指数平滑技术，其计算过程为：

1）计算一次指数平滑序列、二次指数平滑序列为，

其中，平滑系数a可通过分析预测误差加以优选。当原始数据波动较小时，a可以取的小一些，这是为了起平滑序列作用，使波动减小。当原始数据波动比较大的时候，为了使平滑序列反映数据的新变化，a值应取得大一些。

2）计算预测直线的截距和斜率

3）作预测，可以得到：

二阶自适应系数法

与一阶自适应系数法类似，在二次指数平滑基础上，依据预测误差的情况，可以不断地调整平滑系数a ，记为at，即二阶自适应系数法。其计算过程为：

首先设定初值，一般取β=0.1或0.2

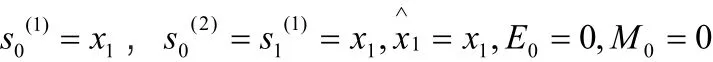
计算自适应系数at

式中et为预测误差。

Et为误差序列e1，e2，…，et的一阶指数平滑，Mt是的一阶指数平滑。

3）可以采用下式来进行预测：

从t=1至t=T，通过循环执行第2）和第3）步，得到预测值此后的预测值将由下式给出：

需要指出的是，在第1）步的初值条件下，e1=0，E1=M1=0，这时应取a1=0或a1=1，无论取哪一个，都有从而但用（2）中无意义，应用求出。以后的计算中，如果遇到a1=1，就用计算。

用于模型检验的后验差检验方法

后验差检验是根据模型预测值与实际值之间的统计数据进行检验的一种模型检验方法，也就是以残差ε作为基础，根据各期残差绝对值大小来考察残差较小点出现的概率以及与预测误差方差有关的指标的大小。现假设历史负荷序列和预测值序列分别为：

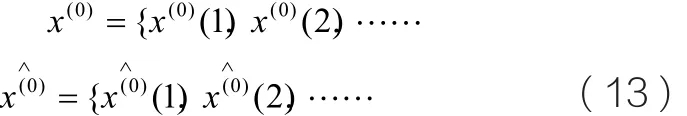
k时刻实际值x（0）（k）与计算值之差为ε（k），称为k时刻残差。

实际值x（0）（k），k=1，2，……，n的平均值为即：

其中，m是残差数据个数，一般来讲m≤n。若历史数据方差记为S12，即有

残差方差记为S22，有

这样可以得到后验差的两个非常重要的数据，即后验差比值C和小误差概率P：

一般认为，后验差比值C是越小越好，因为C越小，表明S1越大而S2越小。S1越大，说明历史数据的方差越大，历史数据的离散程度也就就越大。S2越小，表明残差方差越小，或者说残差的离散程度越小。也就是说C越小，说明尽管历史数据很离散，但模型所得的预测值与实际值之差并不太离散。而小误差概率指标P是越大越好，因为P越大，表示残差与残差平均值之差小于给定的0.6745S1的点就较多。因此我们可以利用C、P这两个重要指标来综合评定预测模型的精度，如表1所示：

表1 预测模型精度等级评价表

算例分析

这里采用我国从1981到1998年的年发电量数据，其中用1981到1994年的年发电量数据进行建模，用1995到1998年的年发电量数据进行预测分析比较验证。图1是我国1981-1994年年发电量数据散点图，从图中可以看出该数据的具有线性趋势，因此可以采用二次指数平滑技术和二阶自适应系数法。

基于二次指数平滑技术的预测实现与模型检验

按照前述计算步骤进行编程，采用matlab软件窗口内的脚本文件M进行编辑，运行仿真，在命令窗口显示仿真的数据结果，并在工作窗口workspace记录下来，并显示图形。将matlab代码加载到软件内运行，记录1981-1994年年发电量的实际值与预测值，建模，运用模型预测1995-1998年年发电量的负荷。实际值和预测值以及它们的误差如表2。

在模型检验中按照前述模型校验方法进行编程，运行程序算出相对误差，分别求出后检验误差参数值C和小概率值P，给出模型等级精度。结果为：后检验误差参数值为：小误差概率：＜0.6745s1=0.6745*1820.1=1227.7｝=1＞0.95。参考预测等级表1，该模型的精度为一级，可以用此模型来预测。

图1 我国1981-1994年年发电量数据散点图

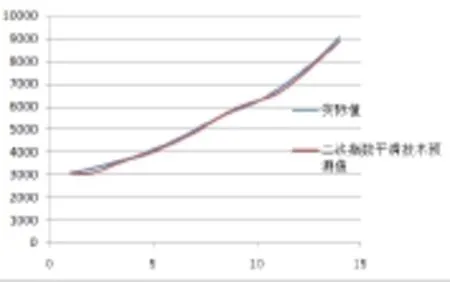
图2 实际值与二次指数平滑技术预测值的比较曲线

基于二阶自适应系数法的预测实现与模型检验

运用matlab软件，按照二阶自适应系数法的算法进行编程，仿真，采用后验差来校验检验模型，进行编程，运行结果，得出模型等级精度，并误差分析。实际值和预测值以及它们的误差如表3。

按照后验差检验算法进行编程，计算出后验差参数C和P值，结果为：

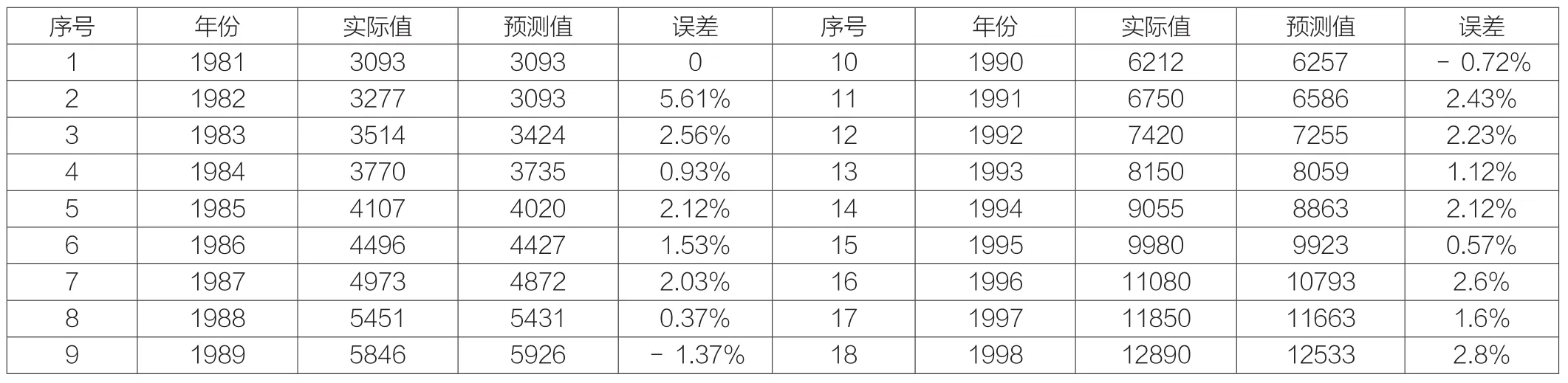
表2 二次指数平滑技术的实际值与预测值（亿kw.h）

表3 二阶自适应系数法的实际值与预测值（亿kw.h）

图3 二次指数的模型预测误差曲线

图4 实际值与二阶自适应系数法预测值的比较曲线

图5 二阶自适应系数的模型预测误差曲线

结语

二阶自适应系数法和二次指数平滑两种模型的预测值和实际值变化趋势相符，而且误差在许可范围内，这两种方法都适合用于中长期负荷预测。虽然模型预测的精度都为一级，但二次指数平滑法的误差比二阶自适应系数法大些。二次指数平滑预测值总有偏移或滞后效应，其平滑系数a为给定值，不能灵活地反映数据变化，当用来预测影响因素较复杂的线性难趋势下的模型时，有时数据波动较大，有时波动又变小，对于给定的平滑系数a值，很难准确地预测未来的负荷，精度很难保证要求。对于二阶自适应系数法，平滑系数a值是依据误差而调整的，采用了误差反馈原理。它能准确地跟随实际值变化的趋势，并给出预测值。若是要按照同样原始数据比较模型的优越性，二阶自适应系数法误差小于二次指数平滑技术，原因在于在二次指数平滑技术的基础上，依据预测误差的情况，不断调整平滑系数a ，记为at。所以说二阶自适应系数发预测效果更好。因此，在电力负荷预测应用中，二阶自适应系数法普遍用来预测线性趋势模型的负荷。

10.3969/j.issn.1001- 8972.2016.21.033