方形截面飞行器上仰机动对滚转特性影响的数值模拟

陈坚强， 陈琦， 袁先旭， 谢昱飞

中国空气动力研究与发展中心 计算空气动力研究所， 绵阳　621000



方形截面飞行器上仰机动对滚转特性影响的数值模拟

陈坚强， 陈琦， 袁先旭*， 谢昱飞

中国空气动力研究与发展中心 计算空气动力研究所， 绵阳621000

飞行器从中小迎角至大迎角范围内，由于背风区流动分离形态的演化，静态气动特性特别是横侧向气动特性也随迎角显著变化，可能诱发复杂的滚转运动。但飞行器一般是上仰机动时，才从平飞状态快速拉起至大迎角，此机动过程对横侧向气动特性和滚转运动可能产生较大影响。本文发展了刚体动力学方程和Navier-Stokes方程的松耦合求解技术,并通过数值模拟航天飞机脱落碎片的六自由度运动轨迹进行了验证。针对背风区涡流形态及横侧向气动特性复杂的方形截面飞行器，数值模拟研究了其不同迎角下的静态滚转气动特性、自由滚转运动特性，以及上仰机动时不同拉起速率对滚转运动特性的影响。结果表明，对于此飞行器，静态时存在临界迎角约为13°，当迎角小于临界迎角时，滚转方向是静不稳定的，诱发快速滚转运动；当迎角大于临界迎角时，滚转方向是静稳定的，其滚转运动是收敛的。但上仰机动时，滚转运动的形态还与拉起速率相关，即使拉起的终止迎角大于临界迎角，如果拉起速率较慢，也可能出现快速滚转运动。

六自由度； 松耦合； 快速拉起； 方形截面飞行器； 滚转运动； 非定常数值模拟

先进高机动飞行器一般都具备快速拉起的机动能力。快速拉起过程可以有效摆脱敌方追踪，取得有利的攻击姿势，或有效提升导弹拦截目标的成功率。快速拉起过程中，由于初始状态(初值)和复杂气动特性(边值)的影响，可能诱发其他自由度的非指令运动，对飞行安全产生影响。从而提出飞行器多自由度耦合运动研究需求。

为了实现对飞行器多自由度耦合运动的风洞试验和数值模拟技术，国内外开展了一系列研究工作。试验方面，美国阿诺德工程发展中心(Arnold Engineering Development Center，AEDC)采用球形气体轴承支撑方式，模拟AIM-9X导弹在气流作用下俯仰、偏航和滚转三自由度的运动过程[1-3]。德国针对X-31模型构建了六自由度的风洞动态试验装置，模型可以实现三个方向的自由转动以及三个平动方向的有限运动[4-5]。中国多家单位也发展了相应的风洞试验技术研究[6-15]。在数值模拟方面，Thomas[16-18]、杨小亮[19-21]、杨云军[22]、张来平[23]、华如豪[24]、索谦[25]等都开展了细致的研究工作。

本文通过建立刚体六自由度动力学方程与Navier-Stokes方程的耦合求解技术，研究上仰机动过程对滚转气动特性和滚转运动特性的影响。研究对象是带4片小翼的方形截面细长体飞行器，定常计算结果与试验值吻合良好，并通过数值模拟航天飞机脱落的泡沫碎片的六自由度运动轨迹考核了建立的耦合模拟技术；分析了方形截面飞行器的滚转气动特性，并通过数值模拟自由滚转运动的过程验证了分析结论；研究了上仰机动过程中气动力的非定常迟滞效应，开展了不同拉起速率对滚转运动特性的影响研究。

1　数值方法和计算模型

本文通过数值求解非定常Navier-Stokes方程，以获取飞行器运动过程的非定常气动力。空间离散格式采用原始变量NND格式[26]，限制器选用min-mod限制器；非定常时间推进采用Jameson[27]的双时间步方法。

采用松耦合的方式解决Navier-Stokes方程和六自由度刚体运动方程的耦合求解问题，刚体动力学(Rigid Body Dynamics， RBD)方程和Navier-Stokes方程分别独立求解，在时间域上交错推进，从而获得耦合系统的响应，求解过程见图1。图中：Navier-Stokes方程的求解标记为计算流体力学(Computational Fluid Dynamics， CFD)系统；RBD方程的求解标记为RBD系统；Q为流场信息变量；ω为动力学变量；x和θ分别为位移和姿态角；F和M分别为气动力和气动力矩。在n时刻，RBD系统将姿态角、位移等传递给CFD系统；CFD系统据此更新动态网格，求解流场，得到n时刻的气动力、气动力矩；CFD系统再将气动力、气动力矩传递到RBD系统，求解得到n+1时刻的姿态角、位移等物理量。重复上述步骤，CFD系统也推进到n+1时刻。

计算模型为方形截面飞行器外形，参考文献[28-29]生成，由一个圆弧形头部和方形截面的机身组成，如图2所示。飞行器总长为13D，D=93.98 mm，头部为切线圆弧，长3D，圆弧半径R=6.717D。机身截面为1D×1D的正方形。机身尾部有4片“十”字布局的三角小翼，小翼的长和高均为D，宽为0.1D。

图1　CFD/RBD松耦合时间推进示意图Fig.1　Schematic diagram of loosely coupling time mar-ching of solution mode of CFD/RBD

图2　方形截面飞行器模型和表面网格Fig.2　Model configuration and surface computational grid of square cross section vehicle

计算马赫数Ma=2.5，以飞行器全长为参考长度的雷诺数Re=1.6×107。力矩参考点在距离头部尖点0.47倍的全长位置。飞行器的转动惯量依据文献[29]试验模型尺寸估算给出，取Jx=0.1，Jy=2.0，Jz=2.0。

2　算例验证

本文的数值模拟工作在自主编制的软件FLY3D上完成，该软件已通过标准算例的测试，在多项基础研究和型号任务中得到应用和考核，本节算例验证工作主要测试本文发展的多自由度耦合算法，并对方形截面飞行器的定常计算结果进行验证。

对航天飞机上脱落的泡沫碎片简化模型，图3 给出了六自由度运动轨迹的模拟结果与试验结果的比较，外形和试验结果参考文献[30]。计算初始马赫数Ma=2.95，初始俯仰角和偏航角分别为6° 和3°，海拔取H=0 km。试验中的角度测量由于是通过高速相机拍下若干时刻的飞行姿态，再通过人工读取的，文献[30]给出的误差带为±4°。可以看到，计算与试验取得了比较一致的结果。

图4则针对方形截面飞行器外形，考核定常的计算结果，给出了两个截面位置的周向压力系数Cp的分布与试验值的比较，计算迎角α=14°，滚转角γ=0°，方位角从飞行器背风面的对称面起算。模拟结果验证了计算程序对方形截面飞行器外形模拟结果的可靠性。

图3　泡沫碎片的欧拉角和平移轨迹预测Fig.3　Euler angle and translation trajectory prediction of foam debris

图4　方形截面飞行器定常计算结果与试验比较Fig.4　Comparison of steady calculation results and test data of square cross section vehicle

3　静态滚转气动特性分析

首先定义“□”型截面姿态为0° 滚转角，“◇”型截面为45° 滚转角，同时定义飞行器顺时针滚转时(从底部往前看)滚转角为正。

图5以10° 迎角为例，给出了不同滚转角时飞行器的流场结构。其中，空间流线用马赫数着色，并给出了不同截面位置总压损失p0s的云图。

由图5可以看到，随着方形截面飞行器姿态从“□”型变化到“◇”型，流场结构经历了对称→非对称→对称的复杂变化过程。

图6给出了0°～50° 迎角范围内，滚转力矩Cl随滚转角变化曲线。

由图6可以看到，在不同迎角下，飞行器滚转特性有很大不同。当飞行器以“□”型姿态飞行时，当迎角小于10° 时，飞行器滚转方向为静不稳定的，且随着迎角增加，滚转方向静不稳定性增强；当迎角位于10°～12° 之间时，滚转方向仍然是静不稳定的，但随迎角增大，滚转静不稳定性减弱；随着迎角继续增大至14° 时，飞行器滚转方向由静不稳定转化为静稳定；继续增大迎角，滚转方向均为静稳定，且随着迎角增加，滚转方向的静稳定性不断增强。

结果表明，对于此飞行器，静态时存在临界迎角αc≈13°，当迎角小于αc时，滚转静不稳定，预测其自由滚转运动应该是发散的；当迎角大于αc时，滚转静稳定，预测其自由滚转运动应该是收敛的。

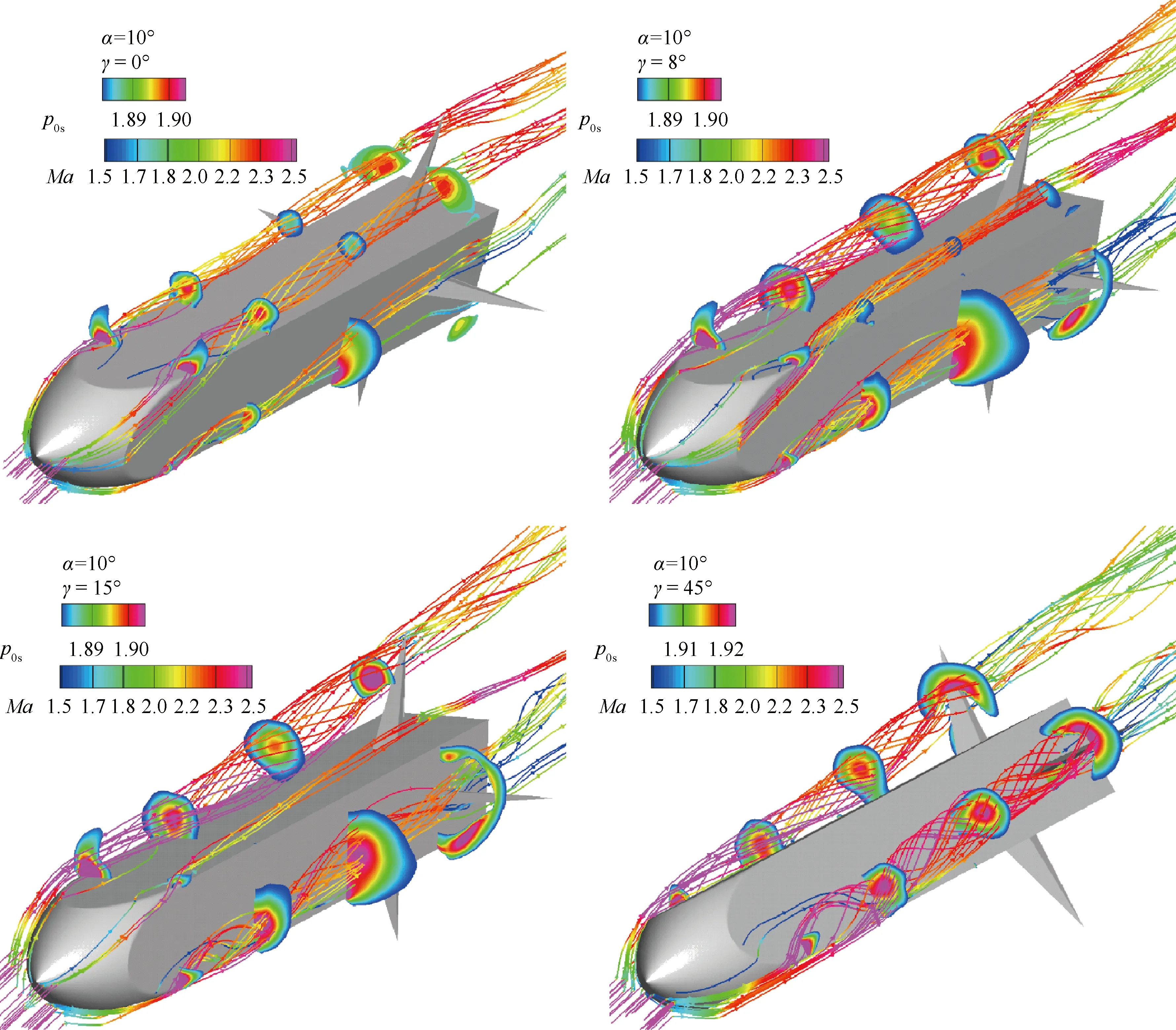
图5　方形截面飞行器不同滚转角时的流场结构(α=10°)Fig.5　Flow structure around square cross section vehicle at different rolling angles (α=10°)

图6　不同迎角时滚转力矩随滚转角变化曲线Fig.6　Variation of rolling moment with rolling angle at different angles of attack

4　自由滚转运动特性分析

针对第3节方形截面飞行器静态滚转气动特性的分析，本节将模拟飞行器自由滚转运动的过程，以验证上述分析结果。

计算迎角分别取10°、14°、20°和40°，无初始滚转角速度，滚转角从5° 位置释放后，飞行器在自身滚转力矩作用下自由振动。图7为模拟得到的滚转角随时间的变化历程曲线，图8为模拟得到的滚转角速度对滚转角的相图。

图7　不同迎角时滚转角随时间变化的历程曲线Fig.7　Time history of rolling angle at different angles of attack

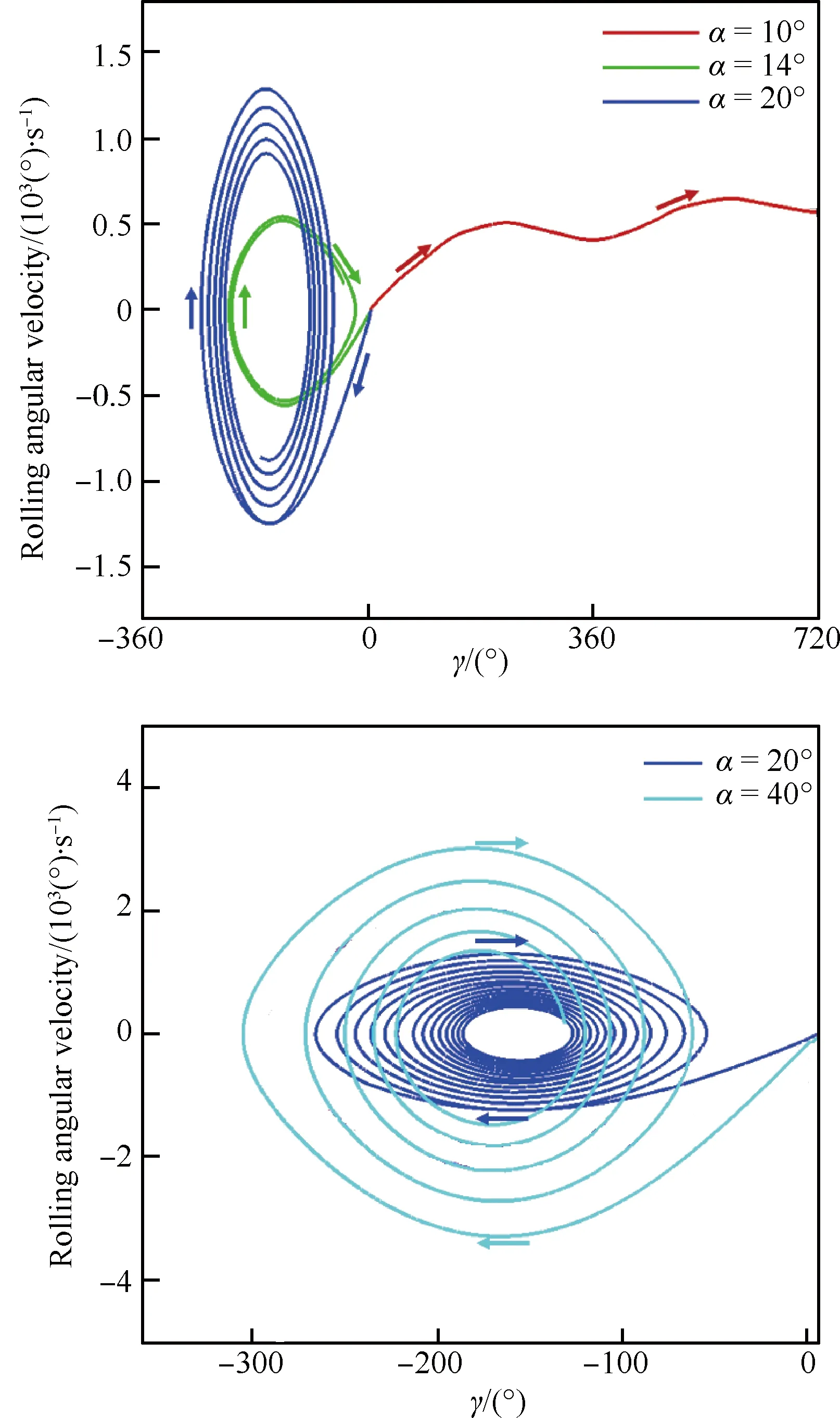
图8　不同迎角时滚转角速度对滚转角的相图Fig.8　Phase diagram of rolling angular velocity torolling angle at different angles of attack

由图7和图8可以看到，在10° 迎角时，由于飞行器的静不稳定特性，滚转角自5° 释放后，飞行器受正方向滚转力矩作用，直接偏离0° 滚转角，形成快速滚转运动。

迎角增大到14° 和20° 时，由于飞行器滚转方向的静稳定性，飞行器沿负方向做滚转运动，但未能稳定在0° 滚转角，而是滚转约180°，之后绕“□”型截面位置振荡收敛。

迎角继续增大后，滚转运动的规律是一致的，均呈现振荡收敛状态；但滚转振动的速率随迎角增大快速增加。这与图6中随着迎角增大，在0° 滚转角位置的滚转静稳定性增强是一致的。

通过对飞行器自由滚转运动过程的模拟，基本验证了静态气动力特性的分析结果；同时，飞行器滚转180° 之后才能稳定的事实表明，飞行器滚转方向的转动惯量可能偏小，稍大的扰动可能使飞行器进入连续滚转运动状态。

5　上仰机动对滚转气动和运动特性的影响分析

5.1上仰机动过程的滚转气动特性

上仰机动过程中，俯仰方向为强迫运动，在指定时间内，将飞行器从0° 迎角拉起到30° 迎角，拉起过程保持匀速，速度分别为60 (°)/s和150 (°)/s；滚转方向保持不动，滚转角为5°。研究上仰过程中飞行器的非定常气动力与定常值的差异。

从图9可以看到：① 非定常上仰过程的滚转力矩与定常值基本一致，上仰过程未引入附加的滚转力矩，表明与飞行器的亚声速上仰过程不同，超声速上仰过程中，气动力对拉起速率的敏感性下降；② 在迎角大于20° 之后，非定常滚转力矩的非线性特性显著，可能对滚转运动产生影响。

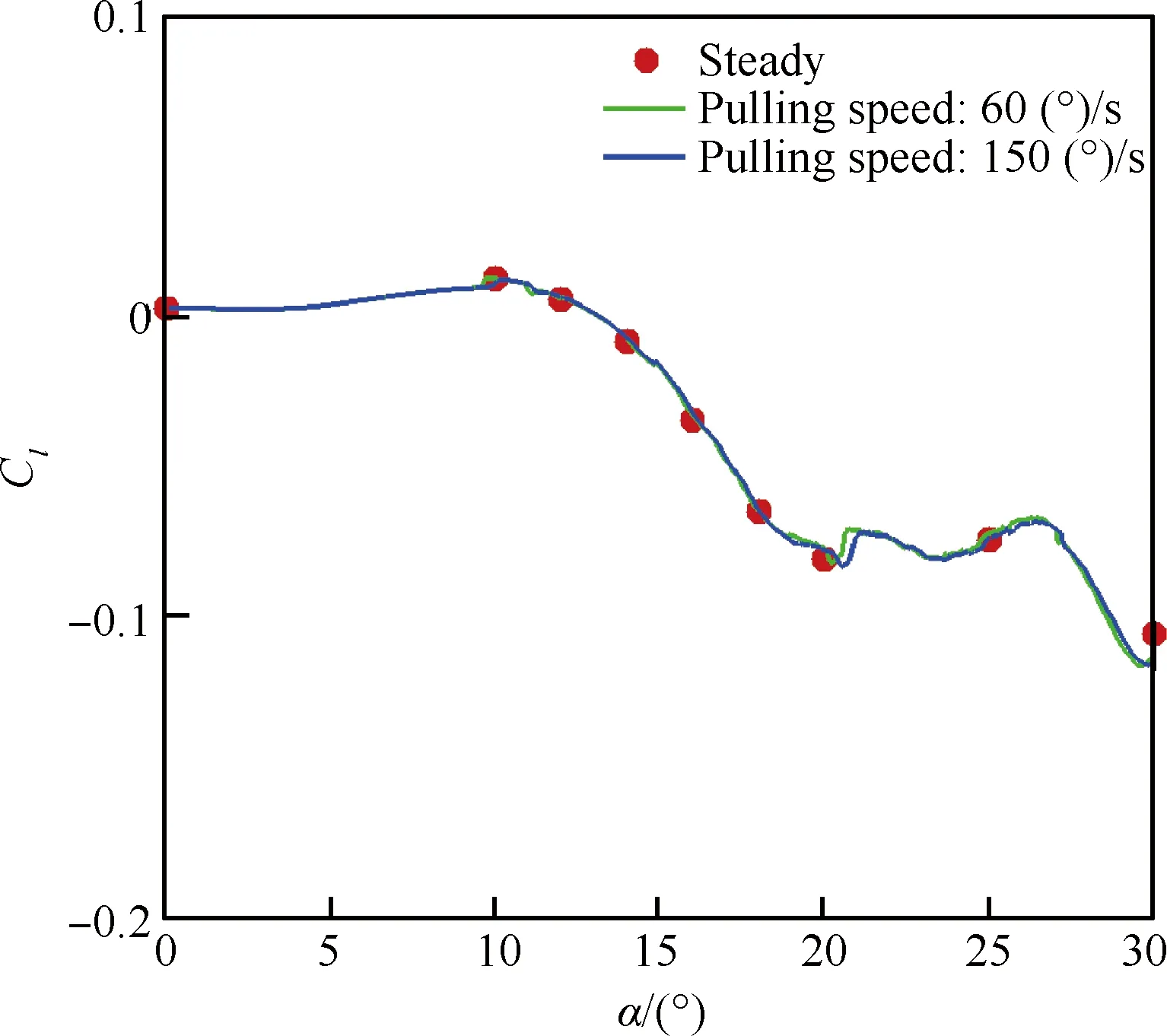
图9　上仰机动过程中的气动力非定常效应分析Fig.9　Unsteady effect of aerodynamics in nose-up process

5.2上仰机动过程的滚转运动特性

上仰机动过程中，俯仰方向的运动方式与 5.1 节一致，同样将飞行器从0° 迎角拉起到30° 迎角，上仰过程结束后，飞行器的迎角将一直保持30°；放开滚转方向的自由度，飞行器在滚转力矩作用下自由运动，起始滚转角γ0=5°。

图10和图11给出了不同拉起速率对滚转运动的影响分析。由于飞行器发生连续快速滚转时，滚转角的变化范围较大，通常在千度以上，为便于分析，在绘图时将滚转角进行转换。滚转角变化范围定为γ=0°～360°，超出范围后将滚转角以360° 取模，转换到该范围中。因此图10中出现一条虚线段连接两条实线段的端点，即表明飞行器绕体轴滚转了一圈，即360°。

根据图10，不同拉起速率对滚转运动的影响很大。拉起速率较小时，飞行器呈连续滚转状态，拉起速率增大到150 (°)/s后，飞行器的滚转运动呈收敛状态。从图11也可以看到，拉起速率为150 (°)/s时，滚转运动为典型的点吸引子形式；当拉起速率为30 (°)/s、60 (°)/s时，拉起结束后飞行器呈快速滚转状态，由于飞行器方形截面的外形，滚转速率围绕稳态值附近振荡。

图10　不同拉起速率对滚转运动的影响Fig.10　Influence of different pulling speeds on rolling motion

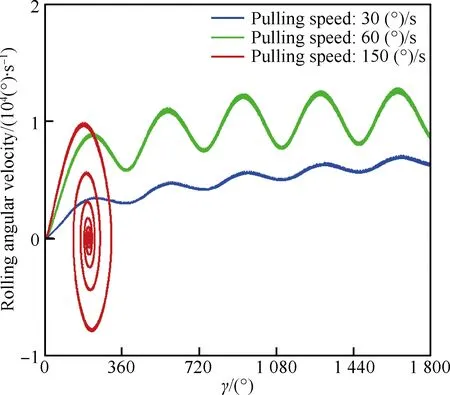
图11　不同拉起速率时滚转角速度对滚转角相图Fig.11　Phase diagram of rolling angular velocity to rolling angle at different pulling speeds

结合图6的模拟结果可以看到，上仰过程开始时，起始迎角为0°，起始滚转角γ0=5°，飞行器初始受到正方向的滚转力矩作用，飞行器的滚转角有向正方向运动的趋势。

拉起速率较快时(150 (°)/s)，飞行器可快速通过滚转静不稳定区域，由滚转静不稳定诱发的滚转角速度较小，到达滚转静稳定区域后，飞行器在自身回复力矩作用下呈现振荡收敛的运动形式。

但如果拉起速率较慢时，飞行器在滚转静不稳定区域持续的时间较长，由滚转静不稳定诱发的滚转角速度较大，即使在回复力矩的作用下，也不足以使飞行器减速并稳定在配平滚转角位置，此时飞行器一般会发展为快速滚转运动。

6　结　论

发展了刚体六自由度运动方程和Navier-Stokes方程的松耦合求解技术并进行了验证，针对背风区涡流形态及横侧向气动特性复杂的方形截面飞行器，数值模拟研究了其不同迎角下的静态滚转气动特性、自由滚转运动特性，以及上仰机动时不同拉起速率对滚转运动特性的影响。主要有以下结论：

1) 飞行器存在临界迎角约为13°，当迎角小于临界迎角时，滚转静不稳定；当迎角大于临界迎角时，滚转静稳定，随迎角增大，滚转静稳定性增强。

2) 根据静态滚转气动特性，可预测迎角小于临界迎角时，滚转运动应该是发散的；迎角大于临界迎角时，滚转运动应该是收敛的。通过自由滚转运动的数值模拟验证了分析的结论。

3) 上仰机动过程，滚转运动的形态与拉起终止迎角的气动特性、初始状态和拉起速率相关。若拉起速率较慢，拉起过程中已经演化出快速滚转运动，即使拉起终止迎角大于临界迎角，其快速滚转运动也不会衰减。这对飞行安全有较大影响。

[1]MAGILL J C, WEHE S D. Initial test of a wire suspension mount for missile virtual flight testing: AIAA-2002-0169[R]. Reston: AIAA, 2002.

[2]MAGILL J C, CATALDI P, MORENCY J R, et al. Demonstration of a wire suspension system for dynamic wind tunnel testing: AIAA-2004-1296[R]. Reston: AIAA, 2004.

[3]MAGILL J C, CATALDI P, MORENCY J R, et al. Design of a wire suspension system for dynamic testing in AEDC 16T: AIAA-2003-0452[R]. Reston: AIAA, 2003.

[4]REIN M, HÖHLER G, SCHÜTTE A, et al. Ground-based simulation of complex maneuvers of a delta-wing aircraft[J]. Journal of Aircraft, 2008, 45(1): 1-7.

[5]BERGMANN A, HUEBNER A, LOESER T. Integrated experimental and numerical research on the aerodynamics of unsteady moving aircraft[J]. Progress in Aerospace Sciences, 2008, 44(2): 121-137.

[6]李志强, 黄达, 史志伟, 等. 俯仰-滚转耦合两自由度大振幅非定常实验技术[J]. 南京航空航天大学学报, 1999, 31(2): 121-126.

LI Z Q, HUANG D, SHI Z W, et al. Test technology of unsteady aerodynamic characteristic for a model oscillating in large amplitude pitching-rolling motion[J]. Journal of Nanjing University of Aeronautics and Astronautics, 1999, 31(2): 121-126 (in Chinese).

[7]李其畅, 伍开元, 郑世华, 等. 高速风洞大振幅俯仰动态试验技术研究[J]. 流体力学实验与测量, 2004, 18(4): 67-77.

LI Q C, WU K Y, ZHENG S H, et al. Investigation of dynamic test technology for a model pitching oscillation with large amplitude in high speed wind tunnels[J]. Experiments and Measurements in Fluid Mechanics, 2004, 18(4): 67-77 (in Chinese).

[8]王兵, 黄存栋, 马宝峰, 等. 精确复现机翼摇滚运动的控制技术[J]. 实验流体力学, 2009, 23(1): 79-84.

WANG B, HUANG C D, MA B F, et al. The control method of precise reproduction of the wing rock motion[J]. Journal of Experiments in Fluid Mechanics, 2009, 23(1): 79-84 (in Chinese).

[9]吕光男. 风洞虚拟飞行试验中的飞行力学与控制问题研究[D]. 南京: 南京航空航天大学, 2009: 19-37.

LV G N. Research on a flight dynamics and control in wind tunnel based virtual flight test[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009: 19-37 (in Chinese).

[10]胡静, 李潜. 风洞虚拟飞行试验技术初步研究[J]. 实验流体力学, 2010, 24(1): 95-99.

HU J, LI Q. Primary investigation of the virtual flight testing techniques in wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2010, 24(1): 95-99 (in Chinese).

[11]陈星阳, 郑鵾鹏. 风洞虚拟飞行试验控制系统设计[J]. 弹箭与制导学报, 2013, 33(6): 129-132.

CHEN X Y, ZHENG K P. The design of wind tunnel based virtual flight testing control system[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2013, 33(6): 129-132 (in Chinese).

[12]向光伟, 谢斌, 赵忠良, 等. 2.4 m×2.4 m跨声速风洞虚拟飞行试验天平研制[J]. 实验流体力学, 2014, 28(1): 65-69.

XIANG G W, XIE B, ZHAO Z L, et al. Development of virtual flight test balance for 2.4 m×2.4 m transonic wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2014, 28(1): 65-69 (in Chinese).

[13]赵忠良, 任斌, 汪清, 等. 风洞模型自由翻滚试验技术[J]. 空气动力学学报, 2000, 18(4): 384-389.

ZHAO Z L, REN B, WANG Q, et al. Wind tunnel test technique of the model free-to-tumble[J]. Acta Aerodynamica Sinica, 2000, 18(4): 384-389 (in Chinese).

[14]陶洋, 赵忠良, 杨海泳. 翼身组合体摇滚特性高速试验研究[J]. 实验流体力学, 2011, 25(6): 45-48.

TAO Y, ZHAO Z L, YANG H Y. Investigation on wing rock of wing-body configuration at high speed wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2011, 25(6): 45-48 (in Chinese).

[15]李浩. 风洞虚拟飞行试验相似准则和模拟方法研究[D]. 绵阳: 中国空气动力研究与发展中心, 2012: 46-75.

LI H. Study on the similarity criteria and simulation method of the wind tunnel based virtual flight testing[D]. Mianyang: China Aerodynamics Research and Development Center, 2012: 46-75 (in Chinese).

[16]THOMAS J P, DOWELL E H, HALL K C. Modeling viscous transonic limit cycle oscillation behavior using a harmonic balance approach[J]. Journal of Aircraft, 2004, 41(6): 1266-1274.

[17]THOMAS J P, DOWELL E H, HALL K C, et al. Further investigation of modeling limit cycle oscillation behavior of the F-16 fighter using a harmonic balance approach: AIAA-2004-1696[R]. Reston: AIAA,2004.

[18]THOMAS J P, CUSTER C H, DOWELL E H, et al. Unsteady flow computation using a harmonic balance approach implemented about the OVERFLOW 2 flow solver: AIAA-2009-4270[R]. Reston: AIAA, 2009.

[19]杨小亮. 飞行器多自由度耦合摇滚运动数值模拟研究[D]. 长沙: 国防科学技术大学, 2012: 150-166.

YANG X L. Numerical investigation of aircraft rock in multiple degrees of freedom[D]. Changsha: National University of Defense Technology, 2012: 150-166 (in Chinese).

[20]杨小亮, 刘伟, 赵云飞, 等. 80° 后掠三角翼强迫俯仰、自由滚转双自由度耦合运动特性数值研究[J]. 空气动力学学报, 2011, 29(4): 421-426.

YANG X L, LIU W, ZHAO Y F, et al. Numerical investigation of the characteristics of double degree-of-freedom motion of an 80° delta wing in force-pitch and free-roll[J]. Acta Aerodynamica Sinica, 2011, 29(4): 421-426 (in Chinese).

[21]杨小亮, 赵云飞, 刘伟. 多种因素对三角翼俯仰/滚转运动特性影响的数值研究[J]. 力学季刊, 2011, 32(1): 28-34.

YANG X L, ZHAO Y F, LIU W. Numerical investigation of multiple sensitive factors of the characteristics of the slender delta wing in force-pitch and free-roll motion[J]. Chinese Quarterly of Mechanics, 2011, 32(1): 28-34 (in Chinese).

[22]杨云军, 崔尔杰, 周伟江. 细长三角翼滚转/侧滑耦合运动的数值研究[J]. 航空学报, 2007, 28(1): 14-19.

YANG Y J, CUI E J, ZHOU W J. Numerical research on roll and sideslip coupling motions about a slender delta-wing[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(1): 14-19 (in Chinese).

[23]张来平, 马戎, 常兴华, 等. 虚拟飞行中气动、运动和控制耦合的数值模拟技术[J]. 力学进展, 2014, 44(10): 376-417.

ZHANG L P, MA R, CHANG X H, et al. Review of aerodynamics/kinematics/flight-control coupling methods in virtual flight simulations[J]. Advances in Mechanics, 2014, 44(10): 376-417 (in Chinese).

[24]HUA R H, ZHAO C X, YE Z Y, et al. Effect of elastic deformation on the trajectory of aerial separation[J]. Aero-space Science and Technology, 2015, 45: 128-139.

[25]索谦, 王刚, 李仑, 等. 基于变步长CFD/RBD方法的旋转弹轨迹仿真[J]. 航空计算技术, 2014, 44(4): 86-90.

SUO Q, WANG G, LI L, et al. Trajectory simulation of a spinning projectile based on CFD/RBD computation method[J]. Aeronautical Computing Technique, 2014, 44(4): 86-90 (in Chinese).

[26]ZHANG H X, ZHUANG F G. NND schemes and their application to numerical simulation of two and three dimensional flows[J]. Advances in Applied Mechanics, 1991, 29: 193-256.

[27]JAMESON A. Time dependent calculation using multi-grid with application to unsteady flows past airfoils and wings: AIAA-1991-1596[R]. Reston: AIAA, 1991.

[28]陈坚强, 陈琦, 袁先旭, 等. 舵面操纵动态响应的数值模拟研究[J]. 力学学报, 2013, 45(2): 302-306.

CHEN J Q, CHEN Q, YUAN X X, et al. Numerical simulation study on dynamics response under rudder control[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(2): 302-306 (in Chinese).

[29]BIRCH T J, PETTERSON K. CFD predictions of square and elliptic cross-section missile configurations at supersonic speeds: AIAA-2004-5453[R]. Reston: AIAA, 2004.

[30]MURMAN S M, AFTOSMIS M J, ROGERS S E. Characterization of space shuttle ascent debris aerodynamics using CFD methods: AIAA-2005-1223[R]. Reston: AIAA, 2005.

陈坚强男， 博士， 研究员， 博士生导师。主要研究方向： 数值计算方法、高超声速复杂流动数值模拟和高超声速飞行器设计及气动性能分析等。

Tel.: 0816-2463011

E-mail: jq-chen@263.net

陈琦男， 博士研究生。主要研究方向： 非定常流动数值模拟、飞行动态特性分析、计算软件开发等。

Tel.: 0816-2463304

E-mail: chenqi@mail.ustc.edu.cn

袁先旭男， 博士， 研究员。主要研究方向：非定常流动数值模拟、 飞行动态特性分析。

Tel.： 0816-2463304

E-mail: xuyan_00@sina.com

Numerical simulation of rolling characteristics in nose-up process ofsquare cross section vehicle

CHEN Jianqiang, CHEN Qi, YUAN Xianxu*, XIE Yufei

Computational Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang621000, China

The vortex of the flow separation at the leeward site is varying momently as the vehicle pulls up to high angles of attack, which may induce strong unsteady effect of aerodynamics and additional lateral aerodynamics. The vehicle is pulled up rapidly from level-off to high angle of attack flight in the nose-up process, which may has prominent effect on the lateral aerodynamics and the rolling motion. To study the unsteady effect of aerodynamics and its influence to rolling characteristics, the loose couple technique of rigid body dynamic equations and Navier-Stockes equations was developed. The established loose couple technique was then validated by simulating the 6-degree of freedom trajectory of debris shedding from the space shuttle. Taking the square cross section vehicle as example, the steady rolling aerodynamic characteristics, free rolling characteristics and the effect of nose-up process at different speeds to rolling characteristics of the aircraft were studied. The results showed that there was a critical attack angle about 13° existing in the free rolling motion, when the attack angle was greater than the critical attack angle, the vehicle was in rapid rolling motion, and when the attack angle was lower than the critical attack angle, the rolling motion was stable. While in the nose-up process, the rolling characteristics were also affected by the pulling velocity, the vehicle could be in rapid rolling motion under the slow pulling speed even the final attack angle was greater than the critical attack angle.

6-degree of freedom; loose couple; rapid nose-up; square cross section vehicle; rolling motion; unsteady numerical simulation

2016-04-21； Revised： 2016-04-29； Accepted： 2016-05-14； Published online： 2016-05-2314:31

s： National Natural Science Foundation of China (11372341, 11532016)

. Tel.： 0816-2463304E-mail: xuyan_00@sina.com

2016-04-21； 退修日期： 2016-04-29； 录用日期： 2016-05-14；

时间： 2016-05-2314:31

www.cnki.net/kcms/detail/11.1929.V.20160523.1431.002.html

国家自然科学基金 (11372341, 11532016)

.Tel.： 0816-2463304E-mail: xuyan_00@sina.com

10.7527/S1000-6893.2016.0150

V211.3

A

1000-6893(2016)08-2565-09

引用格式： 陈坚强， 陈琦， 袁先旭， 等． 方形截面飞行器上仰机动对滚转特性影响的数值模拟[J]． 航空学报, 2016, 37(8): 2565-2573. CHEN J Q, CHEN Q, YUAN X X, et al. Numerical simulation of rolling characteristics in nose-up process of square cross section vehicle[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2565-2573.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

URL： www.cnki.net/kcms/detail/11.1929.V.20160523.1431.002.html