旋转机翼飞机旋翼模式前飞状态干扰气动特性

孙威， 高正红， 姜杰出

西北工业大学 航空学院， 西安　710072



旋转机翼飞机旋翼模式前飞状态干扰气动特性

孙威， 高正红*， 姜杰出

西北工业大学 航空学院， 西安710072

和传统直升机相比，旋转机翼(CRW)飞机在旋翼模式前飞时各部件之间存在更为严重的气动干扰。为了获得旋转机翼/机身/鸭翼/平尾之间的非定常气动干扰规律，基于运动嵌套网格技术，通过求解三维非定常雷诺平均Navier-Stokes(URANS)方程，建立了旋翼前飞流场数值模拟方法。首先对传统直升机旋翼/机身干扰模型进行了计算，验证了方法的可靠性，然后对某旋转机翼飞机全机在旋翼模式前飞状态下的非定常流场进行了数值模拟，并对各个气动部件上的非定常气动力和力矩的变化进行了分析。结果表明：飞机在旋翼模式前飞时，机身部件对旋转机翼的干扰较弱，在经过机身上方时拉力峰值仅略有增加；旋转机翼对鸭翼和垂尾干扰较弱，对机身和平尾干扰较强，随着前飞速度增大，旋转机翼对平尾的干扰会产生较大的升力损失和抬头力矩，需要引起重视。计算结果为该类飞行器的总体综合设计提供了参考。

旋转机翼飞机； 非定常流场； 气动干扰； 嵌套网格； 数值模拟

旋转机翼(Canard Rotor Wing，CRW)飞机是一种先进的高速直升机方案，其最显著特点是具有一副既可以高速旋转作为旋翼，又可以锁定作为固定翼的旋转机翼。波音公司的X-50A“蜻蜓”无人机为该类飞行器的代表，由于旋转机翼锁定之后飞机完全转换为固定翼飞机，旋翼的速度限制不复存在，飞机可以实现真正的高速飞行，应用前景较为广阔[1-2]。

但是，CRW飞机在旋翼模式下的气动特性与传统直升机有很大差异，主要表现在以下3个方面：① 由于要兼顾旋翼和固定翼的使用要求，旋转机翼采用前后对称的椭圆翼型。椭圆翼型的钝后缘使得桨叶即使工作在小的总距角下后缘也会存在非定常流动分离[3-4]；② 由于要考虑固定翼模式的性能要求，旋转机翼设计的比传统直升机桨叶要宽大得多，高速旋转的“机翼”会产生更复杂的涡尾迹。这些涡环绕在机身周围，引起机身气动力的波动，对飞机的操纵性、稳特性和振动水平产生深远影响；③ 由于要考虑过渡模式的安全和平稳性，CRW飞机设计有较大尺寸的鸭翼与平尾用于升力转移。在旋翼模式下，这些部件对下洗气流的遮挡使得旋翼/机身之间气动干扰更强[5]。正是这些强非定常气动特性使得CRW飞机不易控制，著名的X-50A“蜻蜓”的坠机事故[6]也证实了这一点。总而言之，CRW方案要进入实用阶段还需要开展大量的研究，而准确模拟CRW飞机的流场，研究旋转机翼/鸭翼/机身/平尾之间的非定常气动干扰特性具有重要的理论价值和实际意义。

近年来，除了波音公司针对X-50A模型作了试验研究外[7]，大部分文献以数值计算研究为主[8]。国际上，Saeid等[9]曾使用动量源方法对CRW飞机近地悬停时的非定常气动特性进行了研究，但由于动量源方法将旋翼简化为无限薄的圆盘[10]，无法得到桨叶表面的流动细节。很显然，对这类特殊的飞行器，只能通过运动嵌套网格方法求解非定常流场才能准确模拟。中国的Li和Ma[11]采用运动嵌套网格对CRW飞机的干扰流场进行了模拟，但是对模型进行了过度简化：忽略全部机身，并只考虑了悬停状态。

由于X-50A“蜻蜓”无人机的详尽几何参数并未公布，根据仅有的大概尺寸无法对其进行准确建模，本文选取课题组的CRW无人验证机为研究对象，采用运动嵌套网格方法，通过求解三维非定常Navier-Stokes方程对全机旋翼模式前飞干扰流场进行数值模拟，期望揭示旋转机翼与各部件之间的干扰规律。

1　数值计算方法

1.1控制方程

采用三维非定常可压缩雷诺平均方程作为控制方程，在笛卡儿坐标系下可写为

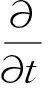
(1)

式中：S为控制体的表面面积；n为控制体边界面外法向矢量；V为控制体的体积；W为状态变量，W=[ρρuρvρwe]T，ρ、u、v、w和e分别为流体的密度、速度矢量在3个坐标方向上的分量和单位体积的总能量；F(W)和G(W)分别为控制体边界面上的对流通量和黏性通量。

时间推进方法采用隐式LU-SGS(Lower-UpperSymmetric-Gauss-Seidel)[12]双时间迭代；空间离散格式采用二阶Roe格式[13]；黏性项采用二阶中心格式离散。本文所有算例均为全湍流计算，湍流模型采用Spalart-Allmaras[14]模型。为了加速收敛，计算中应用了多重网格技术与低速时间项预处理技术[15]。

1.2模型与网格系统

本文选取的CRW无人验证机与X-50A总体布局相同，主要由旋转机翼、机身、鸭翼、平尾以及H型立尾构成。鸭翼为全动形式，尾翼上安装有升降舵和方向舵。旋转机翼为两片无扭转的梯形桨叶，根梢比为2，采用相对厚度为16%的椭圆翼型。旋转机翼半径为R=0.978m，机身总长为3m。为了简化问题，计算建模时忽略了桨毂、起落架以及操作舵面的影响，且不考虑桨叶的挥舞和变距运动。

针对旋翼前飞流场的特点，网格系统采用较为成熟的结构化动态嵌套网格方法。嵌套网格系统分为两个层次，分别是贴体网格和背景网格。建立网格系统的具体步骤如下：

1) 围绕各部件(机身、鸭翼、尾翼及旋转机翼等)生成贴体网格，贴体网格由双曲方程控制生成，为了更好地描述附面层，网格增长率控制为1.1。为了在重叠区域获得相当的网格密度和均匀程度，最外层网格形状基本控制为正方形。

2) 生成背景网格，背景网格为基于逐级二倍加密的笛卡儿直角网格，背景网格最密层间距取为贴体网格最外层网格尺寸。

3) 将贴体网格嵌入到背景网格中建立起网格系统。本文的计算模型与网格如图1所示，网格总量约为1 300万。

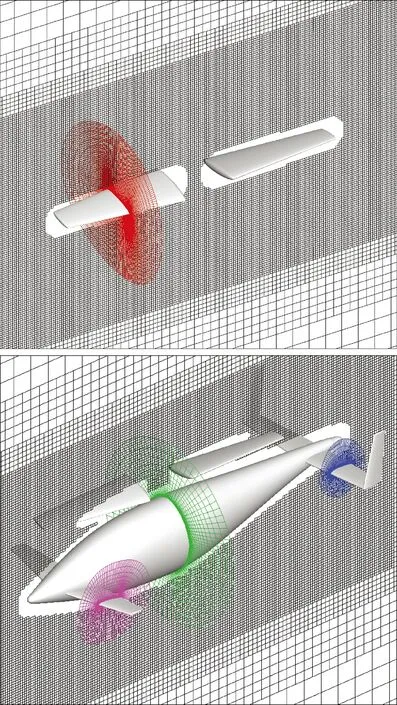
图1　旋转机翼(CRW)飞机计算模型与网格示意图Fig.1　Schematic of computational model and grid for canard rotor wing (CRW) aircraft

1.3洞点识别与插值寻址

网格生成好以后，采用X射线方法实现快速挖洞，其步骤如下：

1) 将物面直接作为挖洞曲面，构造笛卡儿网格块包围挖洞曲面，将笛卡儿网格块底面xOy平面作为像平面，对该平面上所有网格点沿z方向作射线。记录每条射线与挖洞曲面的交点信息。

2) 对于空间任意一点p(xp,yp,zp)，由

(2)

判断p点在像平面中的位置。式中：ip和jp为p点在像平面中的位置索引；xmin和xmax为像平面的横坐标的边界值；ymin和ymax为像平面的纵坐标的边界值。对该位置对应的单元的4个角点作射线，由zp计算p点在这4条射线上的投影点相对于挖洞曲面的位置关系，并用4个参数Bip,jp、Bip+1,jp、Bip,jp+1和Bip+1,jp+1记录(洞内记为0，洞外记为1)。

3) 有了4个投影点与挖洞曲面的位置关系以后，通过双线性插值计算p点与挖洞曲面位置关系的判据Bp：

Bp=C1Bip,jp+C2Bip+1,jp+C3Bip,jp+1+

C4Bip+1,jp+1

(3)

式中：C1～C4为插值系数，其表达式分别为

(4)

式中：Δx、Δy为像平面的网格间距。如果Bp<0.5则p点在洞内，否则p点在洞外。

完成洞点识别之后，通过以下步骤建立自适应叉树(AlternatingDigitalTree，ADT)。

1) 对网格点集建立一个包围它的空间，任取一点A，作为树的根节点，根节点对应整个空间。

2) 用垂直于坐标轴的平面二等分节点A对应的空间区域，得到下一层节点对应的空间区域。

3) 取点B，判断其落入节点A的左子空间还是右子空间，若位于左子空间，则检查左子空间是否为空，若为空将B点插入在A的左子空间，否则继续在左子空间进一步剖分与判断；若B位于右子空间，处理与此类似；其他点的插入过程与B点类似。

ADT建立好以后，通过递归算法，即可快速实现对指定点的查询，在对插值点定位后，采用三线性插值方法实现区域间的流场信息传递：

φ=a1+a2ξ+a3η+a4ζ+a5ξη+a6ξζ+

a7ηζ+a8ξηζ

(5)

式中：(ξ,η,ζ)为插值点在贡献单元中的相对位置，且0<ξ,η,ζ<1；a1～a8为插值系数，由六面体8个顶点处的流场变量确定。

2　数值方法验证

为验证方法的可靠性，本文首先对具有丰富试验数据的ROBIN(ROtor-Body-INteraction)旋翼/机身干扰算例进行模拟。ROBIN旋翼系统是NASA专门针对旋翼/机身干扰问题而设计的，该旋翼系统包含一副四叶桨旋翼和接近真实直升机外形的机身。模型的具体参数见文献[16]。

选取验证较多的状态μ=0.151，CT=0.006 4进行计算，由于本文未考虑旋翼配平，周期变距角取自文献[17]，具体表达式为θ=12.8-8r/R+2.2cosΨ-2.0sinΨ，Ψ为桨叶方位角，指向后机身时为0°。计算模型与网格如图2所示，物面第一层网格高度取0.5×10-5倍机身长度，满足y+小于1。为了更好地捕捉旋翼尾迹的发展，对下游3倍机身长度内的背景网格区域进行了加密。网格单元总量约1 100万。

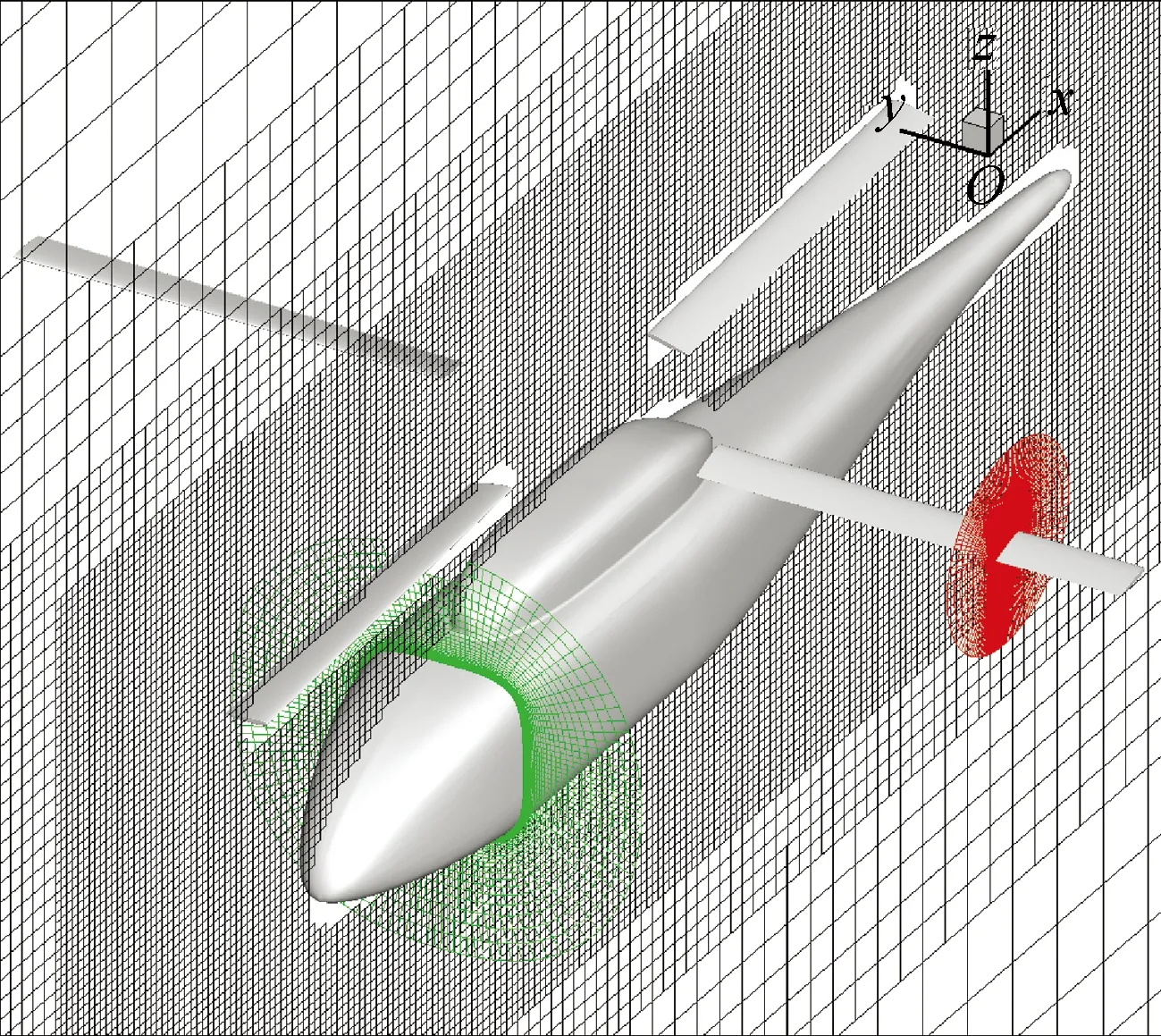
图2　ROBIN计算模型与网格Fig.2　Computational model and grid for ROBIN

机身上表面中线上典型站位测压孔处的压力系数随旋翼方位角的非定常变化如图3所示，瞬时压力系数定义为Cp=100×(p-p∞)/ρ∞(ΩR)2，Ω为桨叶转速，R为桨盘半径。

测压孔x/l=0.096位于机身鼻子上，x/l=0.256位于机头靠近引擎舱处，x/l=1.180和x/l=1.368于机身后部。图3给出了文献[17]中采用FUN3D(FullyUnstructuredNavier-Stokes3D)的计算结果作为对比，其中FUN3D为NASALangley研究中心开发的基于非结构嵌套网格的求解器，是世界上著名的旋翼CFD代码之一。可见本文计算结果基本捕捉到了旋翼与机身之间的气动干扰规律，即每当桨叶扫过机身时，压力就出现一个峰值，相位和振幅都吻合一致。但计算值与试验数据之间误差也较为明显，一个可能的原因是周期变距的不确定性[17-20]。文献中由于对旋翼及机身的支架均进行了建模，计算结果吻合更好，总的来说，采用本文方法能捕捉到旋翼/机身干扰规律，可以用来模拟旋翼前飞干扰流场。

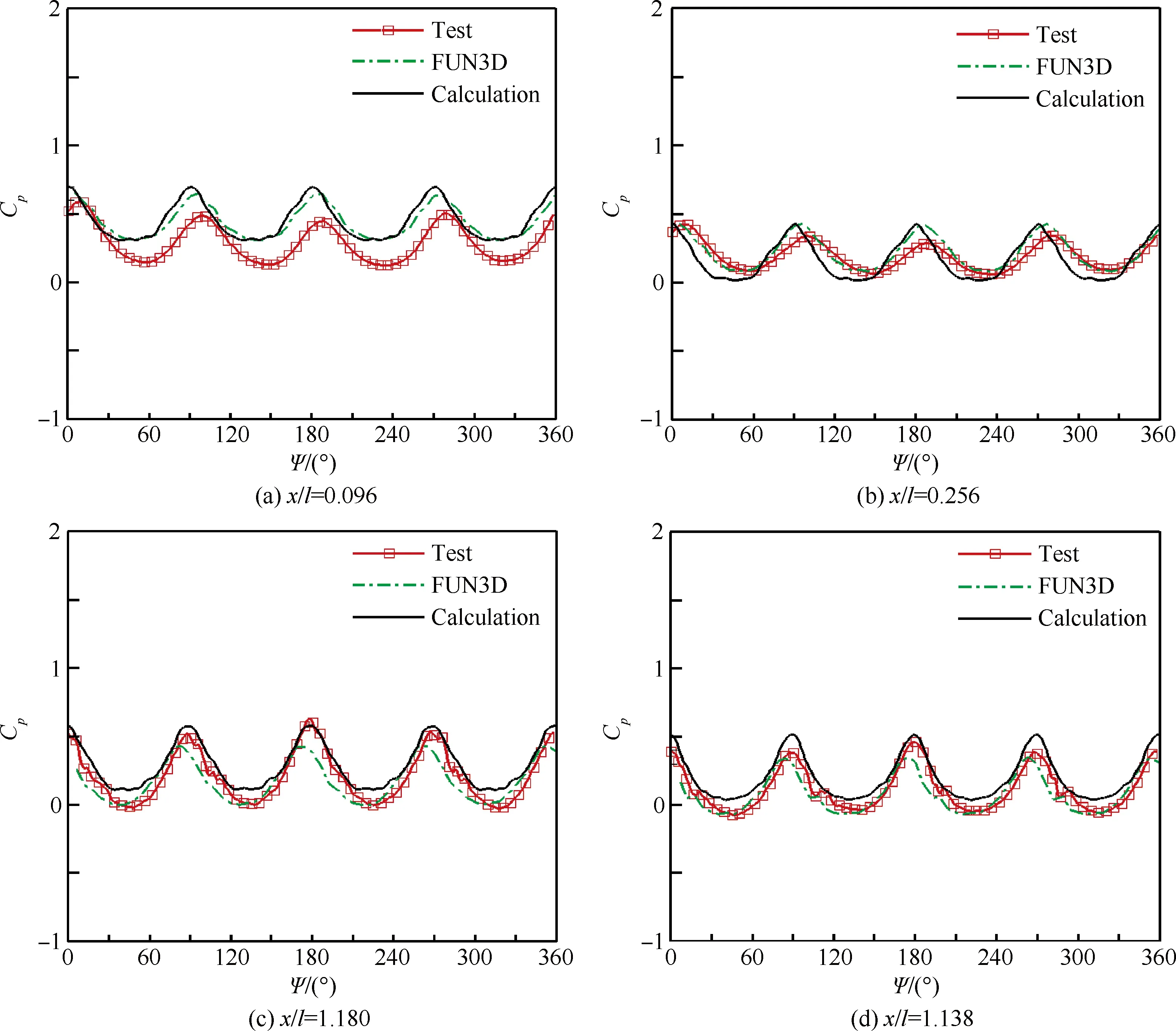
图3　机身上测压孔处的非定常压力系数变化Fig.3　Unsteady pressure coefficient at different fuselage orifices

3　结果与分析

CRW飞机在旋翼模式下主要考虑低速前飞，为了对CRW飞机旋翼模式前飞气动特性有较深刻的理解，本文选取3种前飞状态进行计算作对比。前飞时构造迎角αs=-4°，计算状态如下：

计算状态1：μ=0.05，Matip=0.6，θ=10°，Re=2.095×106

计算状态2：μ=0.10，Matip=0.6，θ=10°，Re=4.190×106

计算状态3：μ=0.15，Matip=0.6，θ=10°，Re=6.285×106

每一个旋转周期被分为180个物理时间步，子迭代步数为20步，以保证子迭代残差至少下降两个量级，为了让旋翼尾迹充分发展，一共计算10个周期。

3.1机身部件对旋转机翼的干扰

旋转机翼与机身部件的干扰主要包括机身部件对旋转机翼的干扰和旋转机翼对机身部件的干扰两个部分，首先对旋转机翼受到的干扰进行考察，为了对比，对单独旋转机翼的情况进行了计算。图4为旋转机翼拉力系数的非定常时间历程(旋转机翼初始位置为Ψ=0°)，表1给出了相应的拉力系数的平均值和振幅对比，拉力系数定义为CT=T/ρ∞(πR2)(ΩR)2，T为旋翼产生的拉力，表中，μ为前进比。总的来看，拉力系数在3个旋转周期后基本达到周期性变化状态。在机身部件的干扰下，拉力系数曲线最主要的变化为当旋转机翼扫过机身时，拉力系数的最大值比单独旋翼的要略大，但旋转机翼远离机身时，拉力系数最小值与单独旋翼的相同，因此拉力平均值和振幅均略微增大，但不明显，且随着前飞速度增大，这一差异越来越小。表明干扰减弱。

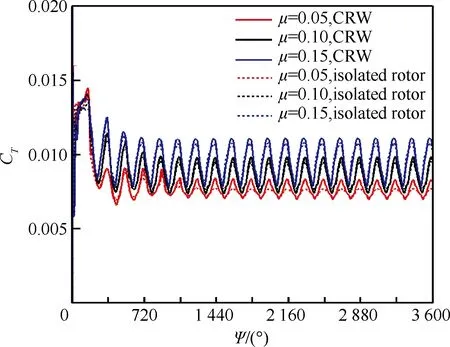
图4　旋转机翼拉力系数的时间历程Fig.4　Thrust coefficient history of canard rotor wing

表1　拉力系数平均值及振幅

Table 1　Mean value and amplitude of thrust coefficient

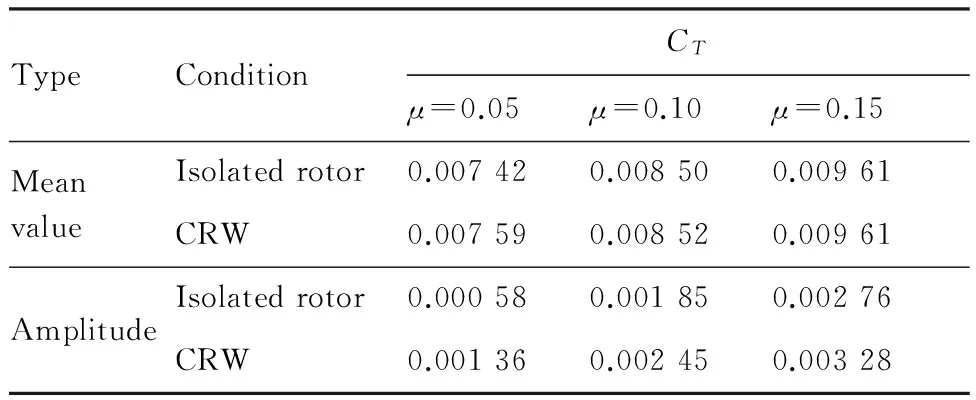
TypeConditionCTμ=0.05μ=0.10μ=0.15MeanvalueIsolatedrotor0.007420.008500.00961CRW0.007590.008520.00961AmplitudeIsolatedrotor0.000580.001850.00276CRW0.001360.002450.00328

3.2旋转机翼对机身部件的干扰

旋转机翼对机身部件的干扰则直接影响整个飞机的飞行性能和操纵品质，图5和图6分别为机身上平均的气动力和力矩随前进比的变化曲线，其中气动力系数的定义为CF=2F/ρ∞(πR2)(ΩR)2，F为机身上的3个方向的气动力，图中CFx为轴向力系数，CFy为侧向力系数，CFz为法向力系数；气动力矩系数的定义为CM=2M/ρ∞(πR2)(ΩR)2R，M为机身上3个方向的气动力矩，图中CMx为滚转力矩系数，CMy为俯仰力矩系数，CMz为偏航力矩系数。力矩参考点位于旋翼中心下方0.585 m处，数值计算结果由最后一个旋转周期取平均得到。

由图可见，随着前飞速度的增大，全机法向力和俯仰力矩发生显著变化，表现为升力损失增大和抬头力矩增大，而其他方向的力和力矩变化不明显，这表明相比于法向力和俯仰力矩，旋转机翼下洗气流对机身其他方向的力和力矩干扰都比较小，因此法向力和俯仰力矩更能反映出CRW飞机旋翼对机身部件的干扰特性。

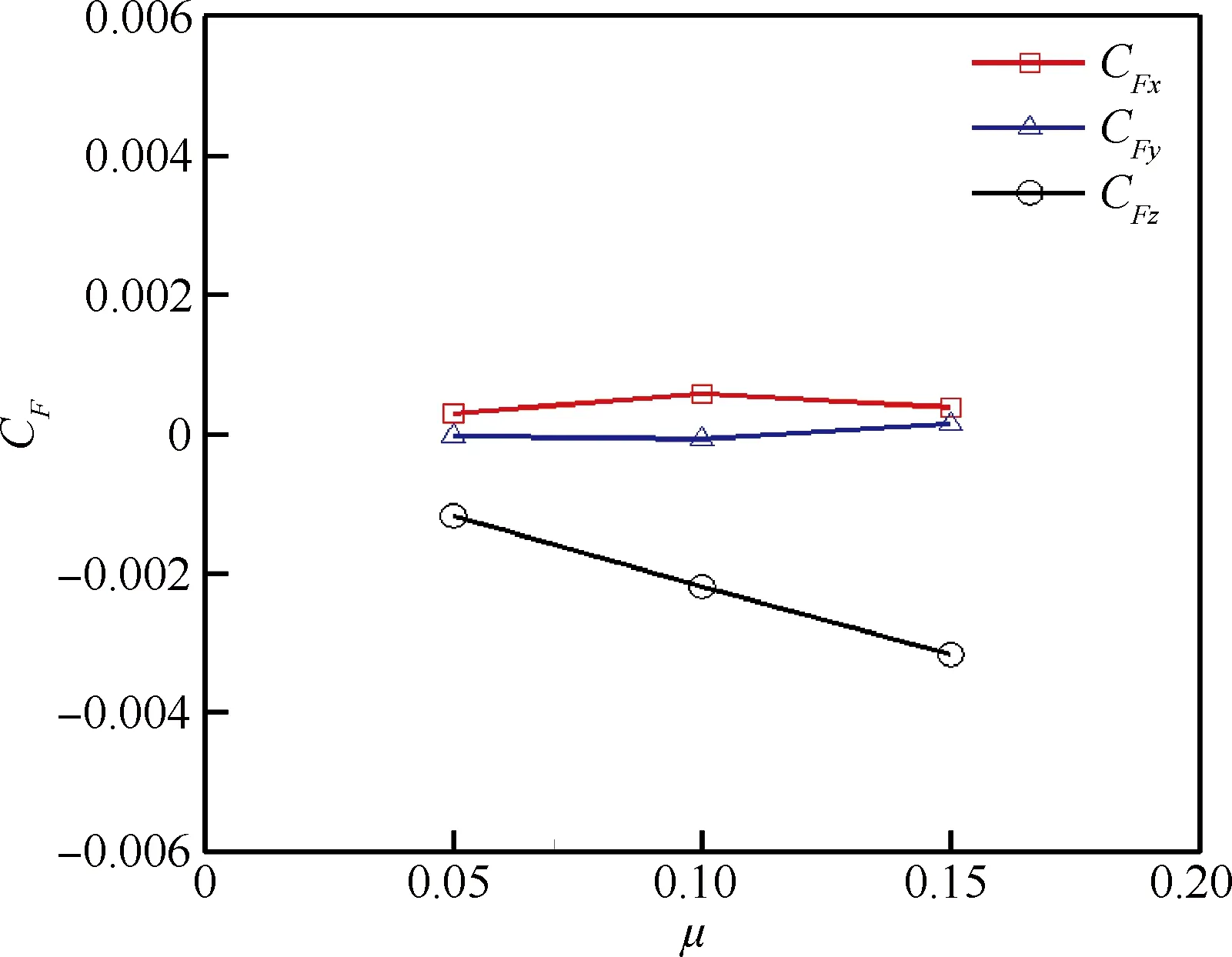
图5　机身平均气动力随前进比的变化Fig.5　Mean aerodynamic forces on fuselage at different advance ratios

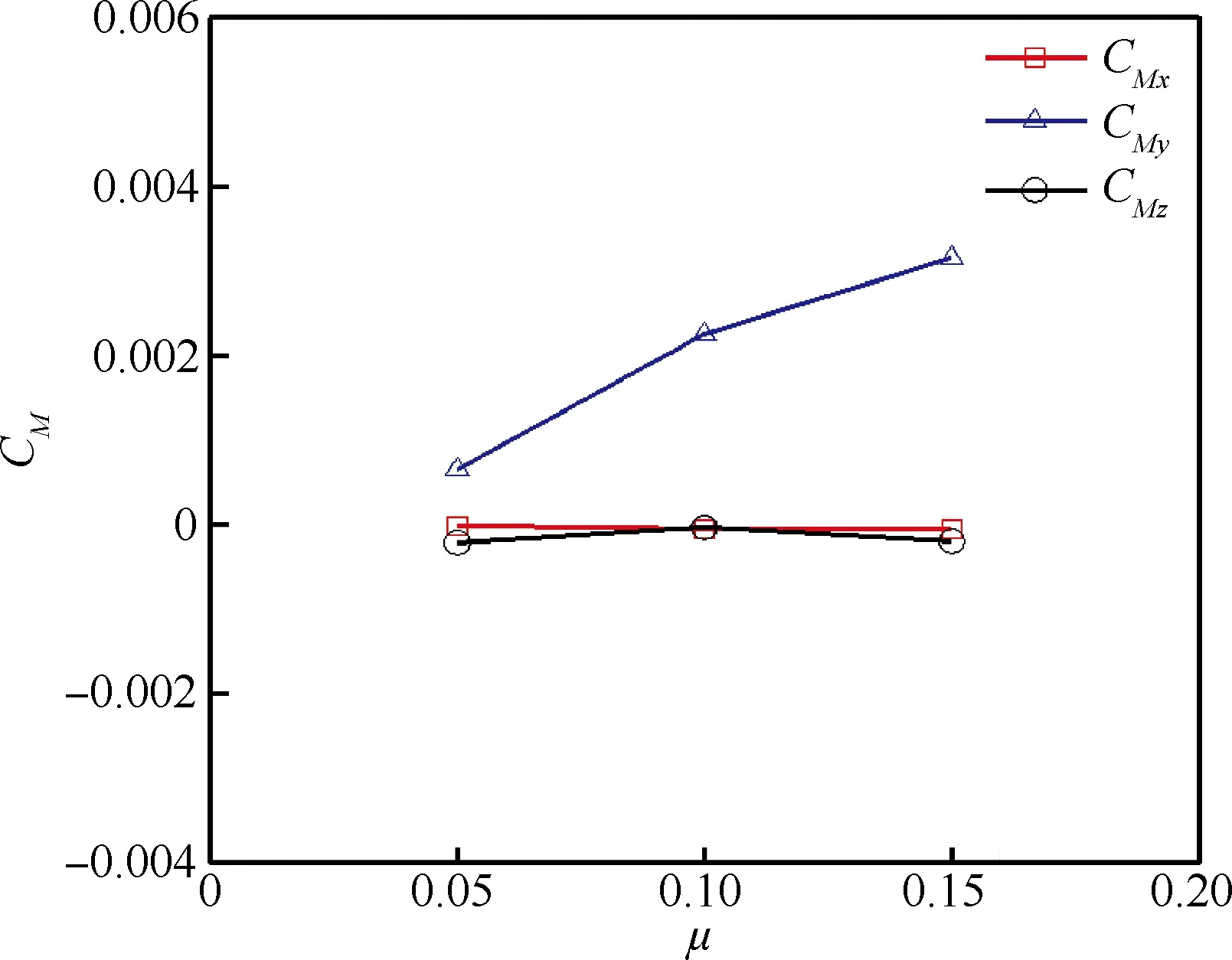
图6　机身平均气动力矩随前进比的变化Fig.6　Mean aerodynamic moments on fuselage at different advance ratios

为了进一步分析旋转机翼对机身部件的干扰特性，图7和图8分别给出了飞机各个部件的法向力系数CFz和俯仰力矩系数CMy在一个旋转周期内的非定常变化。由图7可见，垂尾对法向力的贡献为零，鸭翼和机身上法向力随前飞速度变化不大，相比之下，平尾上的法向力变化最为剧烈。当前进比μ=0.05时，全机的法向力主要来自于机身，当前进比增大到μ=0.10时，平尾上的法向力迅速增大，当前进比增大到μ=0.15时，全机的法向力则主要来自于平尾。由图8可见，由于俯仰力矩主要受法向力影响，其变化趋势与法向力相似：垂尾对俯仰力矩的贡献可以忽略，鸭翼和机身上的俯仰力矩变化不大，平尾上的俯仰力矩变化剧烈。当前飞速度较低时，各部件引起的俯仰力矩相差不多，均维持在较低水平，随着前飞速度增大，平尾上的法向力迅速增大，又平尾的力臂大，因此平尾引起的抬头力矩也迅速增大，导致全机的抬头力矩也迅速增大。

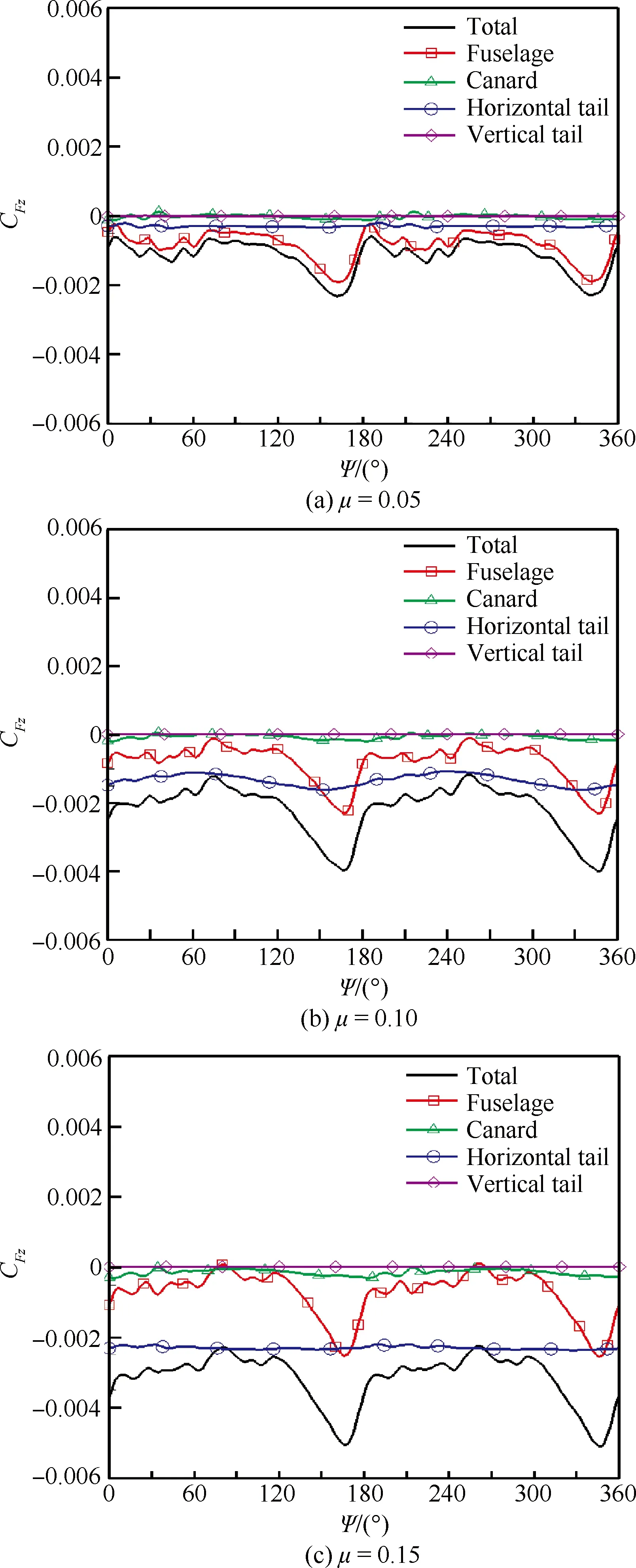
图7　各部件的法向力系数随桨叶方位角的变化Fig.7　Normal force coefficient of each componentvariation as a function of blade azimuth

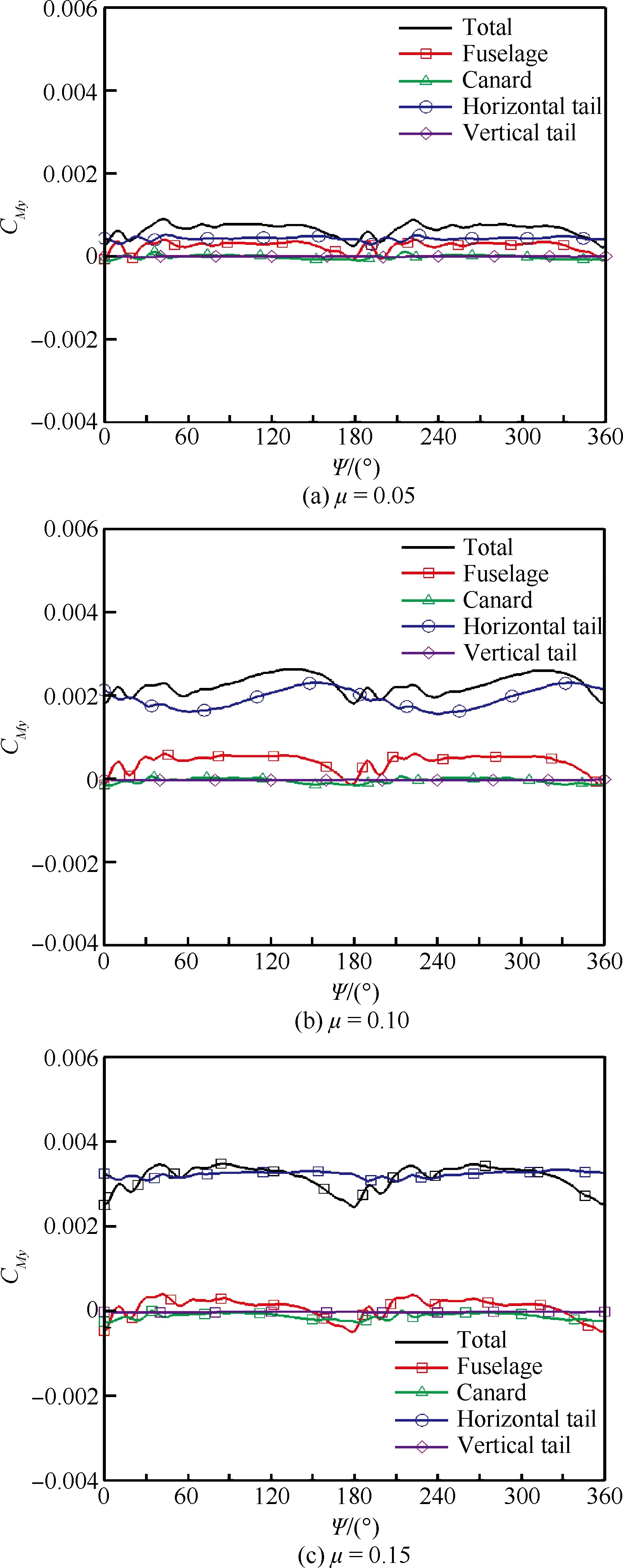
图8　各部件的俯仰力矩系数随桨叶方位角的变化Fig.8　Pitching moment coefficient of each component variation as a function of blade azimuth

众所周知，旋翼对机身部件的干扰主要是旋翼产生的尾迹流动撞击机身部件或者贴近其表面经过所引起的，为了找出法向力和俯仰力矩如此变化的原因，图9通过等Q图(Q=0.01)的形式给出了不同前飞速度下的旋转机翼的尾迹结构示意图，由图9可见，当前进比μ=0.05时，鸭翼尽管处于旋转机翼下方位置，但避开了旋转机翼的下洗流，而平尾离开旋转机翼较远，此时也不在下洗流范围之内，因此全机的法向力主要来自于机身；当前进比增大到μ=0.10时，旋转机翼的下洗进一步后移，平尾进入到下洗流范围之内，下洗气流的冲击使其法向力迅速增加，俯仰力矩也因此迅速增加；当前进比增大到μ=0.15时，平尾几乎与旋转机翼拖出的强烈的桨尖涡处于同一水平位置，下洗气流覆盖了整个平尾表面，因此产生更大的法向力和俯仰力矩。

综合以上分析可以看出，在旋翼模式前飞状态下，随着前飞速度增大，旋转机翼对平尾的气动干扰越来越严重。在下洗气流的干扰下，平尾上将产生一个大的法向力和抬头力矩，这对CRW飞机的稳定性十分不利，在CRW飞机设计中需要重点考虑平尾的设计。理论分析表明，适当调整气动面的位置、面积或者偏转一定的角度可以在一定程度上减小气动干扰，但平尾作为飞机在过渡转换模式下的主要升力面之一，不能采用减小面积的方式来减小干扰，X-50A飞机为了减小前飞时旋转机翼的干扰，将机身后部设计的较为细长，然而这一措施效果甚微，在其第2次试飞时，飞机从悬停转入前飞，很快因抬头力矩过大而失去控制。可见，若干扰引起的抬头力矩过大，偏转翼面角度也不一定能够平衡飞机，因此可以考虑改变平尾的位置以减小旋转机翼带来的气动干扰。

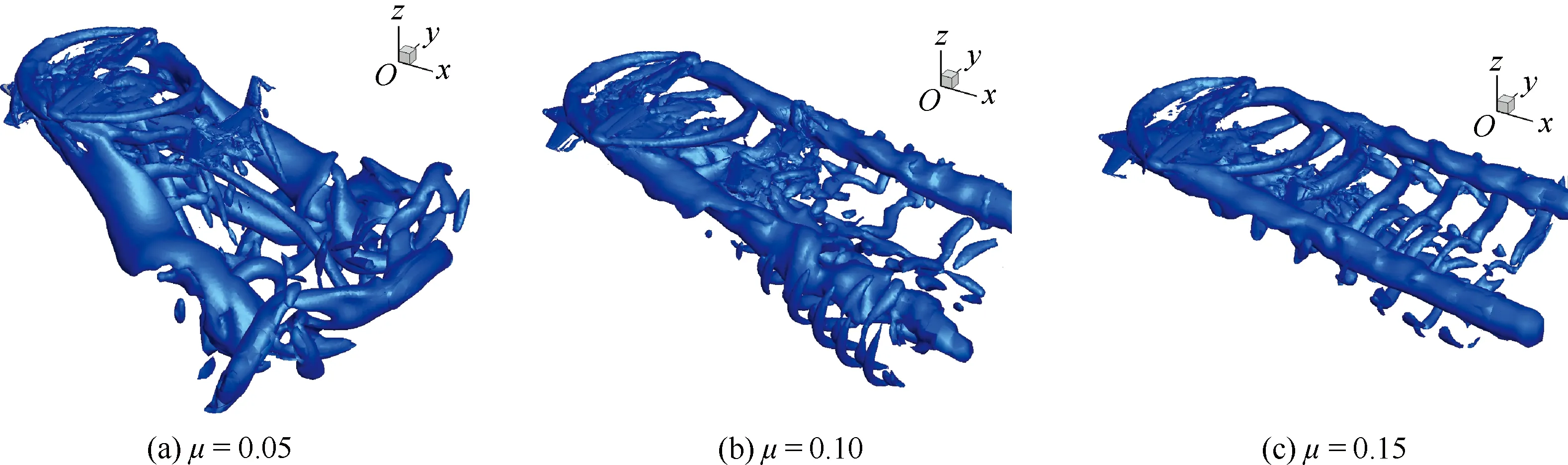
图9　旋转机翼的桨尖涡结构随前进比的变化(Q = 0.01)Fig.9　Blade tip wake structure of canard rotor wing at different advance ratios (Q = 0.01)

4　结　论

1) 本文的方法能较好地捕捉旋翼与机身部件的非定常气动干扰，适合用于旋翼前飞流场数值模拟。

2) 前飞状态下，机身部件对旋转机翼的干扰较弱，当旋转机翼扫过机身时拉力系数峰值仅略微增大，且随着前飞速度增大，这一差异减小，旋转机翼受到的干扰减弱。

3) 前飞状态下，旋转机翼对全机的法向力和俯仰力矩干扰较强，对其他方向的力和力矩干扰较弱。法向力表现为升力损失，俯仰力矩表现为抬头力矩，前飞速度越高，升力损失越多，抬头力矩越大。

4) 前飞状态下，旋转机翼对鸭翼和垂尾干扰较弱，旋转机翼对机身和平尾的干扰较强；随着前飞速度增大，旋转机翼对平尾的干扰越来越严重，平尾的设计在CRW飞机设计中需要重点考虑。

[1]MITCHELL C A, VOGEL B J. The canard rotor wing (CRW) aircraft-a new way to fly： AIAA-2003-2571[R]. Reston: AIAA, 2003.

[2]邓阳平， 高正红， 詹浩. 鸭式旋翼/机翼飞机的技术发展及其关键技术[J]. 飞行力学， 2006, 24(3): 1-4

DENG Y P, GAO Z H, ZHAN H. Development and key technologies of the CRW[J]. Flight Dynamics, 2006, 24(3): 1-4 (in Chinese).

[3]孙威， 高正红， 黄江涛， 等. 旋转机翼悬停气动特性研究[J]. 空气动力学学报， 2015, 33(2): 232-238.

SUN W, GAO Z H, HUANG J T, et al. Aerodynamic characteristics of hovering rotor/wing[J]. Acta Aerodynamica Sinica, 2015, 33(2): 232-238 (in Chinese).

[4]SUN W, GAO Z H, DU Y M, et al. Mechanism of unconventional aerodynamic characteristics of an elliptic airfoil[J]. Chinese Journal of Aeronautics, 2015, 28(3): 687-694.

[5]邓阳平， 高正红， 詹浩. 鸭式旋翼/机翼飞机悬停及小速度前飞气动干扰实验研究[J]. 实验力学， 2009，24(6): 563-567.

DENG Y P, GAO Z H, ZHAN H. Experimental investigation on aerodynamic interactions of canard rotor/wing aircraft in hover and low speed forward flight[J]. Journal of Experimental Mechanics, 2009, 24(6): 563-567 (in Chinese).

[6]MCKENNA J T. One step beyond[J]. Rotor & Wing, 2007, 41(2): 54-56.

[7]THOMPSON T L, SMITH R L, HELWANI M, et al. Wind tunnel test results for a Canard Rotor/Wing aircraft configuration[C]//57th Annual Forum of American Helicopter Society. Alexandria, VA: American Helicopter Society Inc., 2001, 57(2): 1431-1443.

[8]孙威， 高正红. 旋转机翼飞机旋翼/机身干扰流场数值计算分析[J]. 飞行力学， 2011, 29(6): 4-8.

SUN W, GAO Z H. Numerical computation and analysis on rotor/fuselage interactive flow field for rotor wing plane[J]. Flight Dynamics, 2011, 29(6): 4-8 (in Chinese).

[9]SAEID N R, GENESH R, THOMAS L T. Simulation of unsteady aerodynamics of the unmanned CRW dragonfly aircraft hovering near the ground[C]//The AHS International Specialists’ Meeting on Unmanned Rotorcraft. Alexandria, VA: American Helicopter Society Inc., 2005: 439-459.

[10]RAJAGOPALAN R G, FANUCCI J B. Finite difference model for vertical axis wind turbines[J]. Journal of Propulsion and Power,1985, 1(6): 432-436.

[11]LI Y B, MA D L. Numerical simulation of rotor-aerodynamic surface interaction in hover using moving chimera grid[J]. Chinese Journal of Aeronautics, 2012, 25(3): 342-348.

[12]YOON S, JAMESON A. Lower-upper symmetric-Gauss-seidel method for the Euler and Navier-Stokes equations[J]. AIAA Journal, 1988, 26(9): 1025-1026.

[13]ROE P L. Approximate riemann solvers, parameter vectors, and difference schemes[J]. Journal of Computational Physics, 1997, 135(2): 250-258.

[14]SPALART P R, ALLMARAS S R. A one equation turbulence model for aerodynamic flows： AIAA-1992-0439[R]. Reston: AIAA, 1992.

[15]WEISS J M, SMITH W A. Preconditioning applied to variable and constant density flow[J]. AIAA Journal, 1995, 33(11): 2050-2057.

[16]MINECK R E, GORTTON S A. Steady and periodic pressure measurements on a generic helicopter fuselage model in the presence of a rotor:NASA/TM-2000-210286[R]. Washington D.C.: NASA, 2000.

[17]O’BRIEN D M, JR. Analysis of computational modeling techniques for complete rotorcraft configurations[D]. Atlanta: Georgia Institute of Technology, 2006: 121-125.

[18]PARK Y M, NAM H J, KOWN O J. Simulation of unsteady rotor-fuselage interactions using unstructured adaptive meshes[C]//59th Annual Forum of the American Helicopter Society. Alexandria, VA: American Helicopter Society Inc., 2003: 1-11.

[19]TADGHIGHI H. Simulation of rotor-body interactional aerodynamics: an unsteady rotor source distributed disk model[C]//57th Annual Forum of American Helicopter Society. Alexandria, VA: American Helicopter Society Inc., 2001.

[20]CHAFFIN M S, BERRY J D. Helicopter fuselage aerodynamics under a rotor by Navier-Stokes simulation[J]. Journal of American Helicopter Society, 1997, 42(3): 235-242.

孙威男， 博士研究生。主要研究方向： 理论与计算流体力学， 飞行器气动设计。

E-mail: 8532623@163.com

高正红女， 博士， 教授， 博士生导师。主要研究方向： 飞行器气动设计、 计算流体力学和飞行力学。

Tel.: 029-88495971

E-mail: zgao@nwpu.edu.cn

Interactive aerodynamic characteristics of canard rotor wing aircraft in helicopter forward flight

SUN Wei, GAO Zhenghong*, JIANG Jiechu

School of Aeronautics, Northwestern Polytechnical University, Xi’an710072, China

Compared with the traditional helicopter, the aerodynamic interaction of rotor wing, fuselage, canard and horizontal tail of canard rotor wing (CRW) aircraft in forward flight is severer. In order to get better understanding of the unsteady aerodynamic interaction, the moving structural chimera grid is used to model the moving rotor and three-dimensional unsteady Reynolds averaged Navier-Stokes (URANS) equations are solved to simulate the flow fields of rotor in forward flight. The traditional helicopter’s rotor-body interaction model is computed first to validate the method. Then the analyses on rotor wing/fuselage/canard/horizontal tail/vertical tail interactive flow field for an unmanned CRW aircraft in helicopter forward flight are given using the present method. The variations of unsteady aerodynamic forces and moments of the rotor-wing, fuselage, canard, horizontal tail and vertical tail with respect to the rotor azimuth are obtained. The result shows that the fuselage and other components have little effect on the rotor wing, resulting in a slight increase in thrust; the rotor wing has almost no impact on the aerodynamics of canard and vertical tail, but does have strong interference on fuselage and horizontal tail. The horizontal tail produces large vertical force and nose-up pitching moment as the forward flight speed increases, to which great attention should be paid. The research could provide some guidance for the design of a CRW aircraft.

canard rotor wing aircraft; unsteady flow filed; aerodynamic disturbance; overset grids; numerical simulation

2016-01-13； Revised： 2016-02-17； Accepted： 2016-03-14； Published online： 2016-03-2414:12

National Natural Science Foundation of China (11372254)

. Tel.： 029-88495971E-mail: zgao@nwpu.edu.cn

2016-01-13； 退修日期： 2016-02-17； 录用日期： 2016-03-14；

时间： 2016-03-2414：12

www.cnki.net/kcms/detail/11.1929.V.20160324.1412.004.html

国家自然科学基金 (11372254)

.Tel.： 029-88495971E-mail: zgao@nwpu.edu.cn

10.7527/S1000-6893.2016.0092

V211.4

A

1000-6893(2016)08-2498-09

引用格式： 孙威， 高正红， 姜杰出． 旋转机翼飞机旋翼模式前飞状态干扰气动特性[J]． 航空学报, 2016, 37(8): 2498-2506. SUN W, GAO Z H, JIANG J C. Interactive aerodynamic characteristics of canard rotor wing aircraft in helicopter forward flight[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2498-2506.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

URL： www.cnki.net/kcms/detail/11.1929.V.20160324.1412.004.html