飞行器动态稳定性参数计算方法研究进展
2016-11-14刘绪刘伟柴振霞杨小亮
刘绪, 刘伟, 柴振霞, 杨小亮
国防科学技术大学 航天科学与工程学院, 长沙 410073
飞行器动态稳定性参数计算方法研究进展
刘绪, 刘伟*, 柴振霞, 杨小亮
国防科学技术大学 航天科学与工程学院, 长沙410073
动态稳定性参数(简称动导数)是飞行器控制系统设计、飞行器动不稳定发生边界分析及相应动态稳定性判据研究的关键气动参数。在对飞行稳定性问题进行概述的基础上,介绍飞行器动态稳定性参数数值模拟的国内外研究进展。并按照理论方法、工程近似方法及计算流体力学(CFD)模拟方法的动导数发展方向对近年来主要的动导数计算方法进行了综述,评价了各种动导数预测方法的优缺点,指出了动导数数值模拟在理论基础、非定常气动力建模、预测方法精度和效率等方面存在的问题。最后对动导数数值模拟的发展趋势进行了展望。
数值方法; 计算流体力学; 稳定性; 时域分析; 动导数
飞行器设计与开发过程中,获得飞行包线内的动态操稳特性难度大、成本高。激波诱导的流动分离、旋涡的运动与破裂使流体运动呈现强烈的不稳定、非线性特性,通常给飞行器带来超出预期的空气动力学效应,甚至产生某些颠覆性后果[1]。在飞行器设计阶段人们难以预知动态操稳特性的边界以及动态问题的严重程度,在飞行试验阶段暴露出的动态稳定性问题导致了飞行器设计周期成倍增加、设计成本大幅增长以及局部修型带来的不可避免的飞行器性能损失[2]。21世纪以来,飞行器设计中发现存在的动态稳定性问题屡见不鲜[3]。为了更好地从流动机理层面理解飞行稳定性恶化产生的原因,计算流体力学(CFD)方法广泛应用于动态飞行品质问题的研究中[4]。一套成熟可靠的飞行器动态稳定性分析方法可以对不同的飞行器设计方案进行评估筛选,最大程度地降低飞行器设计成本,减少风险[5]。
为解决飞行的稳定性问题,在飞行器设计过程中必须开展飞机运动规律及其在扰动作用下的运动稳定性研究[6]。为了求解描述飞行器运动的六自由度运动方程,需要把气动力负载的影响表示为瞬时运动状态参数及其导数的函数[7]。这样就引出了动态稳定性参数(Dynamic Stability Derivatives),工程上简称为动导数[8]。动导数在实际应用上的需求体现在3个方面[1]:
1) 动导数是飞行器轨道设计时的重要参数[9]。
2) 动导数是姿态控制系统设计中的重要参数[10]。控制系统设计往往以动导数为基础确定放大系数或增益系数。
3) 动导数是飞机动态稳定性分析与飞行品质分析的重要参数。
本文在对飞行稳定性与动导数问题进行概述的基础上,介绍飞行器动导数数值模拟的国内外研究进展。并按照理论方法、工程近似方法及CFD模拟方法的动导数发展方向对近年来主要的动导数计算方法进行了综述分析。最后提出了动导数数值预测技术进一步研究发展的内容。
1 飞行稳定性中的动导数问题
飞行过程中大气湍流、非对称转捩、底部流动干扰及实施机动动作等各种扰动可以引起激波诱导的边界层分离、旋涡的运动与破裂等复杂气动现象,造成飞行器动态稳定性问题。
动导数直接决定了飞行器开环系统受到扰动时振荡的敛散特性。图1给出了飞行器对称定直飞行状态及受扰后的5种运动状态。对无控飞行器来说动导数预测必不可少,直接决定了飞行稳定性。
飞行器闭环系统的稳定性不仅取决于气动稳定性,更主要与控制系统相关,控制系统可以通过姿态面和角速率的反馈来改变系统的稳定性。动导数决定了控制系统的增益系数。如果反馈增益的调节取得太大,虽然飞行稳定性好,但飞行器的机动性能下降,操纵品质与飞行品质变差。飞行器的动态特性具有以下一些主要特征:
1) 飞行器的纵/横向耦合运动导致气动力出现交叉-耦合干扰,产生横侧向稳定性、纵横向耦合稳定性问题。此时横侧向交叉导数,纵横向交叉耦合导数显著影响飞行稳定性。飞行器纵向或横向的振动幅度和频率随运动姿态角及其变化速率呈非线性变化[11],振动过程可能是收敛的,也可能是发散的;振动幅度可能只有几度,也可能大到几十度,甚至发散;振动频率可大可小。
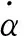
3) 飞行器动态稳定特性对于迎角有强烈的非线性关系,在特殊迎角附近,很小的迎角变化会引起动导数量级的变化,甚至改变符号[12]。

图1 飞行器对称定直飞行状态及受扰后的5种运动状态Fig.1 Aircraft’s steady linear flight state and fivemotion states after disturbance
上述问题的解决依赖于飞行器动态稳定性预测技术的发展。飞行器的动导数计算将为飞行器控制系统设计、飞行器动不稳定发生的边界分析及相应的动态稳定性判据研究提供关键气动参数。
2 动导数计算面临的问题和挑战
目前,随着中国飞行器技术的飞速发展,动导数在工程上的需求也日益增加。表1给出了主要的动态力矩导数[12],表中:Cl、Cm和Cn分别为滚转、俯仰和偏航力矩系数;α和β为迎角和侧滑角;p、q和r分别为滚动轴、俯仰轴和偏航轴的角速度分量。美国在航天飞机的研制过程中对动态参数的风洞试验和数值计算做了大量的工作[1]。几十年来,人们通过理论分析、数值计算和风洞试验,对动导数开展了大量的研究工作,取得了很大的成果,但依然面临精度与效率低、预测种类少、工程化应用经验不足等各方面问题。

表1 主要的动态力矩导数[12]
2.1动导数理论基础及非定常气动力建模
目前,动导数的研究还有许多困难,这些困难很大程度上来自于动态稳定性参数理论上的不完善。长期以来,动导数一直是工程设计中的概念,对于它的确切含义、适用范围和影响动导数的因素,人们的理解还不尽一致。而这种不一致性,造成了实际应用中非定常气动力建模方面的不一致性[1]。
最早的数学模型由Bryan等[13-14]提出。Bryan等认为空气动力和力矩就是扰动速度、控制角度和其速率瞬时值的函数,即
(1)
式中:Cλ为气动力/力矩。
后来Etkin和Reid认为飞行器运动时所受的气动力/力矩系数是状态参数的泛函[15]。这个泛函关系表示为
(2)
式中:L为升力;t为时间。
Etkin模型比Bryan模型更具有普遍意义,但Etkin模型无法解释实际飞行中常见的一些瞬态响应,更不用说解释由于失速造成的气动力/力矩的突变以及由于非定常流动中的分叉、混沌造成的气动力/力矩多值和不确定现象了[16]。针对这一缺陷,Tobak和Schiff[17-18]采用指示函数作为气动力的泛函,得到气动力与状态变量之间的普遍函数关系,建立了确定非定常气动力的指示函数法[19]。虽然Tobak和Schiff根据指示函数的概念对气动力的表述形式在数学上是完备的,但非线性指示函数的确定非常困难,不可能直接求解这个微分积分系统,因此必须对其进行简化处理[20]。
任玉新等利用Tobak和Schiff的非线性指示函数的方法,首先得出气动力/力矩的指示泛函表达式,然后以此为基础,讨论气动力/力矩和相空间变量之间的函数关系,发展了改进的Etkin模型[21]。对于一般的运动形式,气动力/力矩系数Cλ是状态变量α、β、p、q、r及其各阶导数的函数,即
(3)
(4)
式中:下标“0”表示在基准状态下的取值,其中所有的偏导数为改进的Etkin模型中的动导数。
Cowley和Glauert认为[22],Bryan和Etkin模型的气动参数并不随着时间变化。在非定常气动研究中,这一假设经常受到他人的质疑[23-24]。改进的Etkin模型与原模型相比在基准状态参数中包括时间t,计算或测量出的动导数一般是随时间变化的,这一点和动导数的含义相一致。为了更好地描述动态特性在大振幅时出现的非线性特征,文献[25]基于改进的Etkin模型,采用参数化的动导数概念建立了非定常气动参数模型。
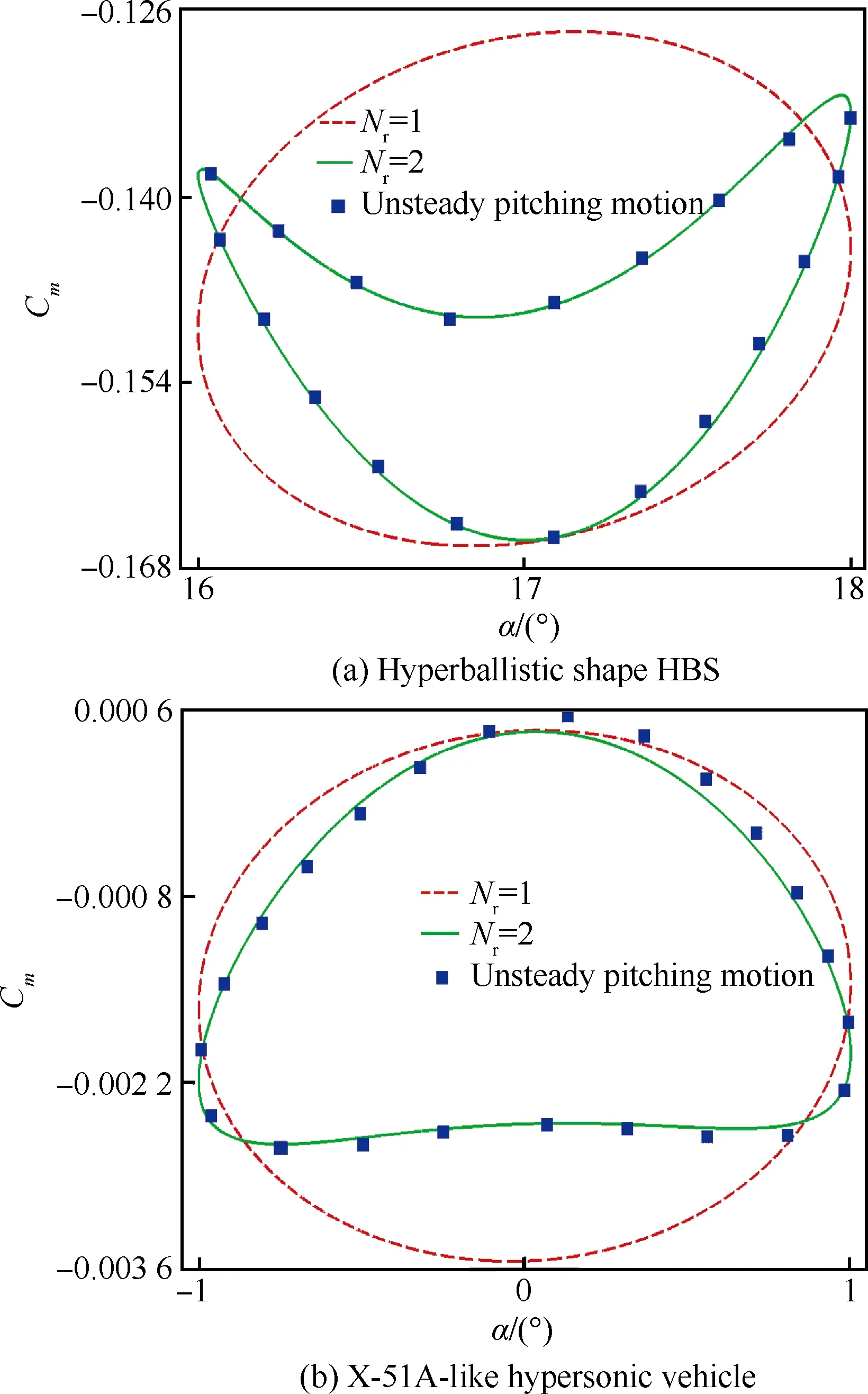
图2和图3分别给出了采用参数化动导数模型预测的类X-51内外流一体化外形和钝锥标模的非定常运动与时域计算的对比结果。图2中:σ为总压恢复系数;αm为振幅。图3中:dθ/dt为俯仰角速度。图中的曲线为非定常时域计算数据,数据点表示参数化的动导数模型计算得到的非定常数据。从图2给出的复杂内外流一体化外形的气动力和流场参数的对比来看,参数化的动导数模型与CFD预测的强迫振动非线性结果基本一致,取得了较好的效果。图3也同时反映出参数化的动导数模型对自由振动力矩系数的计算与时域方法的计算结果吻合。综合强迫振动和自由振动的初步模拟结果,采用基于参数化动导数概念的气动模型来表达非线性条件下的气动力数据及流场参数能够达到较好的精度。
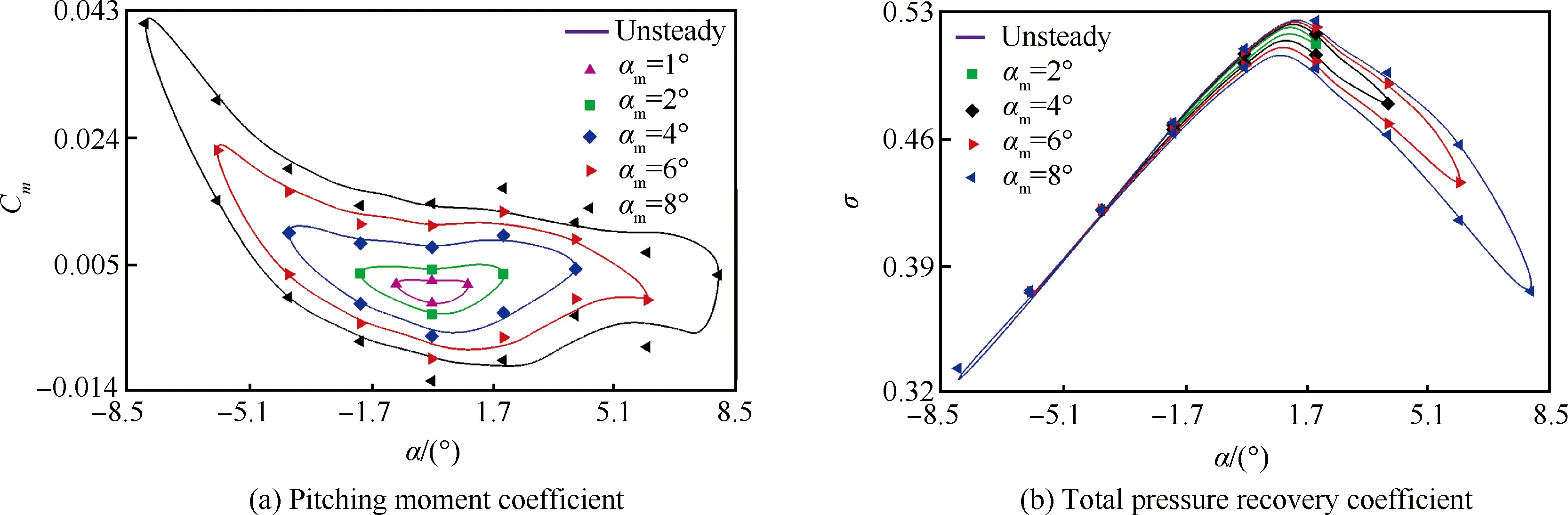
图2 类X-51外形大振幅强迫振动迟滞环曲线Fig.2 Large-amplitude vibration hysteresis curves of a X-51A-like hypersonic vehicle
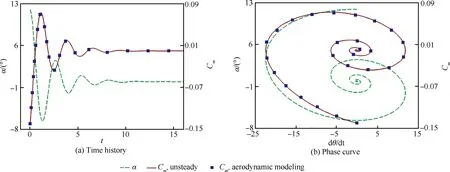
图3 钝锥标模自由振动的时间历程和相曲线Fig.3 Free vibration time history and phase curves of a blunted cone calibration model
2.2动导数计算的精度和效率
动导数与非定常空气动力学密切相关,非定常流场的准确模拟是动导数计算的重要基础。20世纪50年代至90年代期间,细长体理论(Slender-Body Theory, SBT)[26]、升力面理论[27]和牛顿理论[28]等工程算法是动导数计算采用的主要方法。其优点是效率高,但精度较低。为了弥补这一缺点,1969年Hui提出了动导数求解的摄动法[29],精度有了明显提高。随着现代战斗机的机动性、敏捷性及作战效能的提升,对于大迎角或有侧滑角的飞行,复杂的非定常流动现象对动导数有重要影响[30],工程算法和摄动法依然难以满足动导数的求解精度。
随着CFD的成熟发展与广泛应用,20世纪90年代后期基于CFD的动导数计算方法得到了蓬勃发展。任玉新等[31-32]通过求解非惯性系下的欧拉方程和敏感性方程,发展了基于敏感性分析的气动稳定性导数数值计算方法,并在三维问题中得到应用[33]。刘伟等数值模拟了飞行器的强迫简谐振动,发展了滚转阻尼导数[34]、偏航阻尼导数[35]和俯仰阻尼导数[36]的数值计算方法。袁先旭等[37-39]数值计算了HBS(Hyper Ballistic Shape)外形、尖/钝锥外形以及飞船返回舱的俯仰动静导数,预测动态失稳现象、临界参数和失稳后的极限环运动形态[40]。21世纪以来,随着CFD动网格技术的进一步发展应用,史爱明[41]和卢学成[42]等采用非结构动态网格重构技术计算了超声速导弹的动导数,陶洋等也使用动态变形网格对Finner导弹[43]及方形截面导弹[44]的动导数进行了数值计算。此外范晶晶[45]、陈东阳[46-47]和黄龙太[48]等也使用不同CFD工具对包括翼型、有翼导弹以及多种实际的飞机模型进行了动导数计算,得到了与风洞试验值吻合较好的结果。
模拟飞行器强迫/自由振动的CFD方法最大的困难是效率较低。非定常计算效率成为CFD在动导数方面应用的瓶颈,迫切需要开展动导数高效计算方法研究。飞行包线内的气动力和力矩数据量级能够达到数十万至数百万,并且预测动导数需要计算与时间相关的动态非定常气动响应,因此目前采用CFD求解一条飞行包线上的动导数数据所花费的代价非常昂贵。在飞行器及流动问题比较复杂的情况下,计算耗费往往难以忍受。
目前在飞行器型号设计初期,动导数的工程近似方法依然是满足动导数快速分析需求的重要手段[49]。此外,国内外针对动导数的CFD高效计算方法也开展了相应研究。蒋胜矩等[50]在物面无滑移边界条件的基础上施加物面绕体轴的切向速度,通过求解定常Navier-Stokes(N-S)方程得到了滚转阻尼导数,提高了计算效率。准定常计算方法[51]和非定常频域计算方法[52]也相继应用于动导数的计算。但这类方法均为非定常时域方法的简化近似,其适用范围及计算精度有待于深入研究。此外,还应进一步开展CFD时域方法中与高性能计算机体系结构相适应的大规模并行技术研究[53]、CFD加速收敛技术研究[54]、基于Kriging差值的加速方法研究[55-56],在保证动导数计算精度的前提下提高计算效率。
2.3不同类型的动导数预测
在飞行器姿态控制系统设计及轨道(弹道)设计中,所需要的动导数有数十个之多。对于不同的气动构型或研究不同的问题,表1中各个动导数的重要性会有所区别。目前国内外文献主要是研究绕定轴振动时俯仰、偏航或滚转3个方向的直接阻尼导数,而对交叉导数、交叉耦合导数、加速度导数及旋转导数的数值计算较少涉及。
2.3.1交叉导数和交叉耦合导数
如第1节所述,交叉导数和交叉耦合导数是反映飞行器纵横向交叉耦合效应和横侧向交叉效应的重要参数,文献[57]给出了其计算方法。但相对于直接阻尼导数,交叉导数和交叉耦合导数的不确定度较高。这是因为这类动导数量级比较小,并且需要数值方法能精确模拟流动非对称现象。目前计算和试验对交叉导数和交叉耦合导数预测经验不足,计算和试验的对比数据较为缺乏。应进一步开展这方面研究,提高交叉导数和交叉耦合导数预测的可靠性。
2.3.2加速度导数和旋转导数
直接阻尼导数是旋转导数和加速度导数的组合。马东立和叶川采用CFD方法研究了带翼潜航器[58]及升力浮力复合型飞艇[59]的加速度导数,指出了两种外形均不能将加速度导数简化为附加质量系数。文献[25]计算了美国海军旋转稳定式火箭弹ANSR(Army-Navy Spinner Rocket)及内外流一体化外形的加速度导数,结果表明在某些情况下反映流动时滞效应的加速度导数占直接阻尼导数的比例最高可以达到40%以上,而在某些情况与直接阻尼导数符号相反。米百刚[60]和席柯[61]等针对加速度导数的研究也得到了类似结论。
总的来说,目前动导数的研究大多围绕绕定轴振动的组合导数,针对加速度导数和旋转导数的研究较少,现有的结论也大多基于纵向阻尼导数。关于这部分研究特别是飞行器横侧向的加速度导数,仍有大量工作要做。
2.4动导数在复杂外形中的工程应用
文献中常见的动导数计算外形大多采用较为简单的旋成体外形,例如尖/钝锥、HBS导弹、Finner标模、M910子弹。针对较为复杂的真实工程外形较为少见。马东立和叶川开展了带翼潜航器[58]、升力浮力复合型飞艇[59]、有翼导弹和水上飞机[62]的动导数计算。文献[25]开展了类X-51A内外流一体化外形的动导数计算。针对工程外形的动导数计算的困难取决于非定常流场的复杂程度。例如在超声速条件下,激波诱导分离、旋涡运动与破裂以及它们之间的相互作用使得流动形态十分复杂。高超声速内外流一体化外形飞行器从助推火箭分离到发动机点火的短时问内,飞行器经历3种工作状态:进气道关闭、进气道开启和喷流状态。研究发动机不同工况的飞行稳定性对内外流一体化构型设计具有重要意义。
目前的动导数模拟效率不能满足复杂工程外形的动导数计算需求。对真实工程外形的复杂非定常流场的精确模拟是动导数计算的重要前提,也是构成飞行器动态稳定性问题的复杂性和艰巨性的重要原因。
3 动导数理论及工程计算方法
3.1理论计算
动导数的理论计算早期针对一些比较简单的物形,比较简单的运动为研究对象,目前随着数值计算的发展已不再采用。理论方法都建立在许多苛刻的简化假定的基础上,如位势流理论、小扰动线化理论等。Theodorsen[63]最早在1933年利用不可压无黏流假设下给出了二维机翼(NACA0012)做简谐运动时非定常气动力的表达式,计算得到了俯仰力矩的时滞导数和旋转导数。
3.2工程近似方法
动导数的工程近似方法考虑了线化的空气动力学理论和经验关系[64],是一种经验和半经验的方法。工程近似方法与CFD方法相比精度较低,但其最大的优势在于快捷高效[65],因此在飞行器概念设计阶段,通常采用工程估算快速获得飞行器的气动特性[66]。
图4给出了5口径美国海军旋转稳定式火箭弹ANSR采用SBT[67]与强迫振动CFD[25]求解的动导数对比。ANSR模型结果显示,SBT在动导数的预测趋势上与CFD符合,但数值上存在量级甚至符号的差别,仅在个别点处取得一致。East和Hutt[68]通过对比高超声速导弹标模HBS以及尖/钝锥标模外形的动导数试验与工程计算结果,指出工程方法依赖于经验性,只适用于不考虑边界层转捩、流动的分离和再附以及复杂背风区涡流情况下的小迎角线性范围。
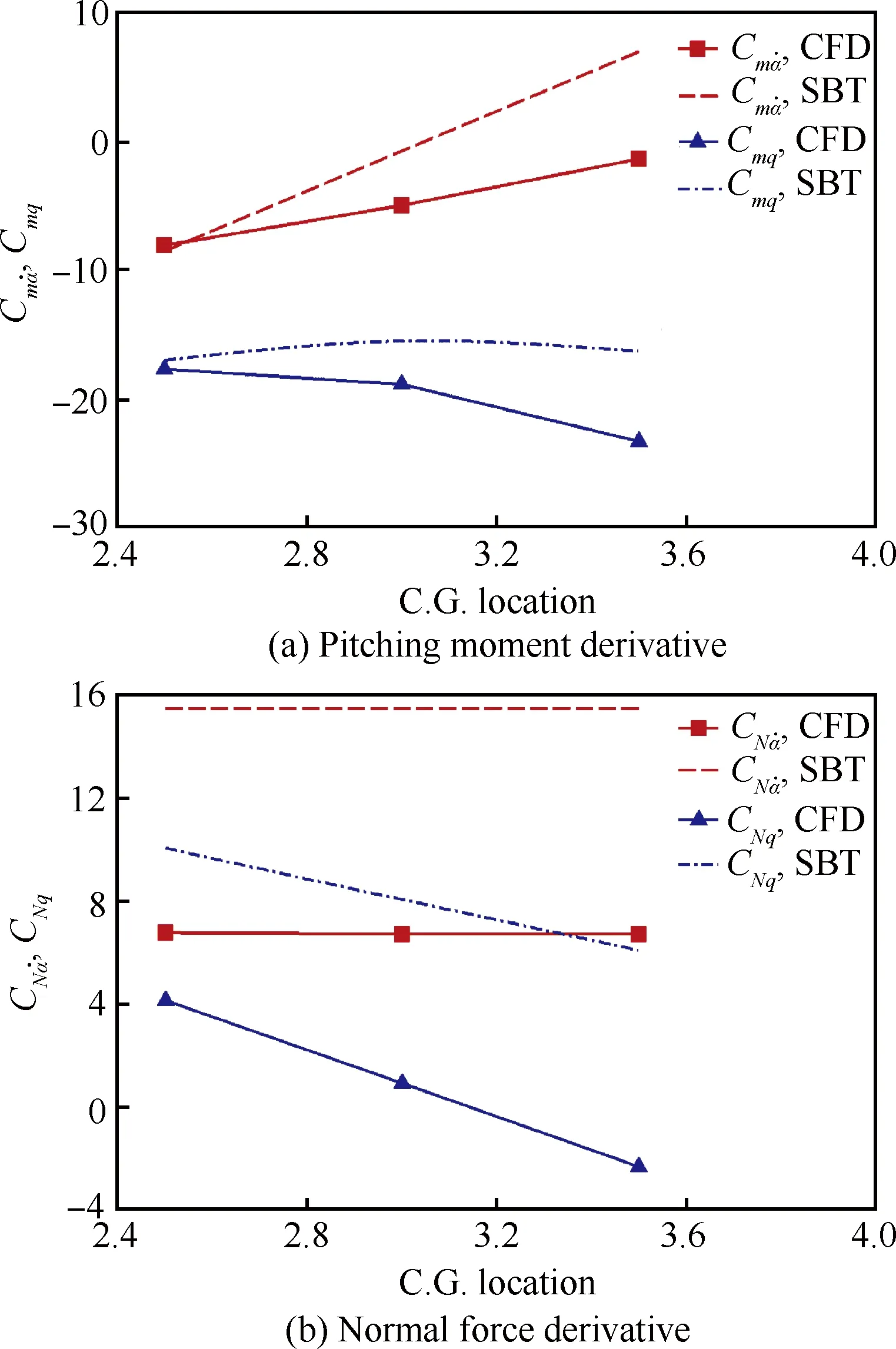
图4 细长体理论(SBT)与CFD强迫振动求解结果对比Fig.4 Comparison between results obtained from slender-body theory (SBT) and those from CFD forced vibration algorithm
工程近似方法在亚声速时以SBT和升力面理论为主[69],而超、高超声速时主要集中于活塞理论、激波/膨胀波比拟以及修正牛顿理论、内伏牛顿理论(Embedded Newtonian Method)、牛顿-玻尔兹曼理论等一些基于牛顿理论发展而来的方法[70-71]。对于纵向动导数可以提供亚、跨、超声速范围的工程近似方法。对横航向动导数主要提供亚声速情况下的工程近似方法,关于跨、超声速下的横航向动导数,目前尚无合适的估算方法[72]。确定动导数的半经验方法可参见飞行力学书籍[73],以及相关的飞机设计手册[74]。下面针对工程近似方法中最重要的牛顿理论和基于CFD技术的当地活塞理论展开综述。
3.2.1牛顿理论
牛顿理论只能用于高超声速流动,其理论假定流体粒子间互不干扰,它们与物面碰撞后,法向动量传给物面,且沿物面以零切向加速度运动。对牛顿理论的一个简单的半经验修正为
(5)
式中:(Cp)MNewt为牛顿理论半经验修正的压力系数;Cpmax为驻点压力系数;Vn为垂直物面的流体运动速度;V∞为来流速度。Tobak和Wehrend最早在1956年用修正的牛顿理论计算了锥体的动导数[75]。
牛顿理论有很大的局限性。Busemann[76]认为,在激波层中,流体粒子的轨迹是弯曲的,在计算物面压力时,必须考虑由此引起的离心力效应。
Psurface=PNewt+Pcent
(6)
式中:Psurface为物面压力;PNewt为牛顿理论计算出的压力;Pcent为离心力修正。Hui[29]针对有脱体激波的三角翼,求解定常参考流动时,使用了Messiter的薄层激波近似[77]。Hui注意到,非定常牛顿流理论加上离心修正时,与比热比γ→1、马赫数Ma→∞时的气体动力学理论完全一致[78]。在这个基础上,Hui和Tobak[79]发展了非定常的牛顿-波尔兹曼理论,用来计算翼型、楔和锥体的动导数。
牛顿-波尔兹曼理论适用于马赫数很高,激波层很薄且充分靠近壁面的情况。对于钝头体,这个条件不能满足。为了解决这个问题,一些基于牛顿或牛顿-波尔兹曼理论的半经验方法得到了发展。Seiff在1962年提出了内伏牛顿流理论来处理有限厚度激波层中的流动[80]。Ericsson[81]发展了Seiff的理论[80],来处理非定常流动,并用来计算高超声速飞行器的动导数。后来,Ericsson[82]改进了自己的方法,进一步降低了马赫数的限制,Ericsson的方法通常称为非定常内伏牛顿流理论。
国内的童秉纲(Tong)和Hui把牛顿-波尔兹曼理论和非定常的内伏牛顿流理论结合起来,发展了半经验的非定常内伏牛顿-波尔兹曼理论[71],对高超声速钝头体的动导数进行了研究。刘伟和沈清[83]利用非定常内伏牛顿计算倒锥体的俯仰阻尼导数,可应用于3 3.2.2活塞理论 活塞理论适用于超声速非定常气动力计算,压力p采用式(7)计算。 (7) 式中:p∞为来流静压;w为下洗速度。活塞理论经过Van Dyke[84]和Lighthill[85]的发展,已经被广泛应用于非定常气动力的计算。陈劲松[86]根据当地流活塞理论和片条理论给出超声速和高超声速尖前缘三维机翼俯仰导数的近似解析方法,在菱形翼、双圆弧形翼及三角翼中得到应用。 为了提高活塞理论的计算精度,张伟伟等[87-88]发展了基于CFD技术的当地流活塞理论。该方法只需要用CFD方法求解一次定常流场,再运用活塞理论计算非定常气动力,充分发挥了CFD技术高精度和当地流活塞理论高效率的特点。2013年张伟伟等[89]在前述工作的基础上,发展了超声速、高超声速外形动导数的活塞理论求解方法,并通过Finner标模及尖锥外形开展了标准算例验证。图5给出了尖锥外形俯仰阻尼导数的内伏牛顿理论、活塞理论与试验结果的比较[89],反映出内伏牛顿理论与基于CFD技术的当地流活塞理论的计算结果在数值上基本相同,内伏牛顿理论结果与试验值更加接近。 图5 内伏牛顿理论、活塞理论与试验结果动导数对比[89]Fig.5 Comparison of dynamic derivatives between those obtained with embedded Newton method, piston theory, as well as test results[89] 4.1谐振摄动方法 摄动法又称小参数展开法。Hui发展的摄动法[90]有两个特点:① 基于Euler方程;② 可同时用于超声速和高超声速流动。其基本过程是在谐振假定下,飞行器绕某一点在平衡位置附近作小振幅简谐振动时的非定常流场可以分解为平衡位置的定常绕流流场及小扰动流场的线性叠加。在一阶近似下,扰动流场的确定可以进一步简化为求解扰动量振幅的类Euler方法。该方程是线性的,且与定常绕流的Euler方法有相同的系数矩阵。求解定常绕流的Euler方程和振动振幅方程均采用相同形式的差分格式,然后利用不同轴间动导数转换公式求得指定轴处的俯仰阻尼导数[91]。 Hui利用他发展的摄动法对简单形状的翼、楔、和零迎角锥进行了计算[29],Hui等还研究了俯仰运动机翼气动力的分叉现象[92]和时间历史效应对高超声速运动的楔受到的非定常气动力的影响[93]。刘秋生和沈孟育[94]进一步发展了Hui的方法,计算了超声速、高超声速钝头体的俯仰阻尼导数。张才文[95]采用Euler方程摄动解法,推导了在激波附体的条件下任意迎角、任意平面形状机翼的超、高超声速俯仰稳定性导数的计算公式。刘伟和张鲁民在文献[94]的基础上发展了俯仰轴在垂直于俯仰平面任意移动时的动导数转换公式[96],并采用谐振摄动法计算了类返回舱外形的高超声速俯仰阻尼导数[97],结果表明,谐振摄动法对简单外形及小迎角来流状态具有较好的适应性,但由于小扰动方法本身的局限性,该方法对复杂外形应用能力有限。如果要计算更为复杂的流态,应该考虑流场的黏性效应及更为一般性的动导数计算方法。 4.2锥运动方法 Schiff等将锥运动引入稳定性导数计算[98-99]。在非惯性参考系下,通过利用定常流动的计算方法模拟非定常问题进而避免了计算开销及动网格等技术问题,用此办法获取了轴对称导弹的俯仰阻尼导数。Weinacht等[100-101]也发展了通过在非惯性系下求解的方法将动态问题转换为静态计算而获取了轴对称导弹稳定性导数。Despirito等[102]在2009年提交美国军方研究实验室(ARL)的报告中总结了采用锥运动法计算美国海军旋转稳定式火箭弹ANSR、M910式25 mm 曳光脱壳训练弹(TPDS-T)以及0.5口径子弹的动导数结果。 图6给出了采用抛物化的Navier-Stokes方程求解ANSR标模锥运动方法(PNS)[67]与CFD强迫振动[25]求解的动导数对比。二者在数值大小及变化趋势上差别不大。锥运动方法虽然简化了计算,提高了计算效率,但其通常不适合非轴对称的复杂外形几何体或仅适用于零迎角时动导数的计算,工程中较少使用。 图6 锥运动方法(PNS)与CFD强迫振动求解结果对比Fig.6 Comparison between results obtained from cone motion method (PNS) and those from CFD forced vibration algorithm 4.3准定常方法 旋转导数的计算可以采用准定常方法。通过求解飞行器绕定轴以恒定角速度转动的准定常方程获得旋转导数为 (8) 席柯等[61]采用准定常方法计算了HBS外形和Finner基本带翼导弹标模外形及Hyflex升力体外形的旋转导数。张一帆等[103]采用准定常方法,对F12全机模型的3个迎角进行了动态特性数值模拟。米百刚等[104-105]采用准定常方法计算了Finner外形的滚转旋转导数,计算误差为2.67%。 图7给出了采用准定常与非定常强迫振动方法求解旋转导数的对比。5口径与9口径的ANSR旋成体外形的Cmq结果如图7(a)所示,类X-51复杂外形的Cmq与φq(φ代表流量系数)[25]结果如图7(b)所示。无论是简单的旋成体外形还是复杂的内外流一体化外形,准定常方法与非定常强迫振动方法对气动力导数和流场参数导数的计算精度基本保持一致。准定常方法仅适用于旋转导数的计算,不能用于加速度导数和组合导数,应用上存在不少限制[25]。 图7 准定常方法与强迫振动求解结果对比Fig.7 Comparison between results obtained from quasi-steady motion and those from forced vibration algorithm 4.4强迫振动方法 强迫振动方法采用CFD方法数值模拟飞行器不同的强迫振动,得到非定常振动流场及气动力,通过数值辨识方法计算动导数[106]。该方法能计算表1中所有类型的动导数,求解精度高,对复杂的非定常流场有较好的适应性,不受飞行状态、模型运动形式及支架洞壁干扰的限制。目前CFD方法代表非线性空气动力学特性预测的最先进水平[107],通过数值计算获得动导数是当前飞行品质和操稳特性研究中一种最理想、最现实的方式,且可靠性有望接近飞行试验。 计算不同的动导数类型需要采用不同的强迫振动形式。任玉新[108]给出了动导数通用计算方法NEASD,在满足状态变量线性无关的条件下,该方法可以求解飞行器做任意强迫振动时的动导数。孙涛等[109]给出了强迫等速拉伸运动时动导数计算的差分法。强迫振动计算动导数最常用的形式为强迫简谐振动。图8是飞行器3种非定常强迫简谐振动(俯仰/沉浮/拍动)的飞行姿态和运动轨迹示意图[25]。 图8 非定常运动示意图Fig.8 Unsteady motion sketch (9) 式中:α0为初始迎角;θm为俯仰角振幅;k为减缩频率。 (10) 强迫拍动简谐振动用于计算俯仰力矩旋转导数Cmq,其振动方程为 (11) 沉浮与拍动两种振动方式的叠加等于俯仰简谐振动。通过计算式(10)和式(11)产生的时域数据进行后处理来辨识得到动导数。后处理方法包括积分法、频域变换法、回归方法和相位法。积分法、频域转换法和回归方法的后处理结果没有显著的差异,但在减缩频率较小的情况下回归方法比其他方法得到的结果精确。相位法只采用了时域数据的两个点,因辨识误差大而较少使用。 强迫简谐振动的优点是计算精度高,适用于不同种类的动导数辨识。缺点是存在减缩频率相似及简谐振动振幅的选择问题。虽然线化的模型方程要求气动参数的变化保持在线性范围内,但过小的振幅显著降低了数值仿真过程中气动参数的增量,增加了随机误差的比例,带来了精确预测动态气动参数的困难[110]。文献[111]认为合理的振幅选择需要综合评估小振幅振动的线性范围以及非定常计算本身的精度。孙涛等[109]分析了减缩频率对Finner标模动导数计算的影响。强迫振动测试中频率的选择没有普遍的原则或共识。通常认为频率应该是最具代表性的预期的飞行器运动频率[112]。 飞行器在大气层中以高马赫数飞行时,其表面摩擦阻力系数会达到总阻力系数的50%以上。2004年,刘伟等[113]研究了平衡气体效应对带翼飞行器俯仰阻尼导数的影响。赵文文等[114]在2013年对比分析了不同高度(含稀薄气体效应)、Maxwell滑移边界条件及五组元化学非平衡模型对钝锥体模型动导数的影响。高空、高马赫数条件下飞行器动导数的计算还需做进一步深入的研究。 为了研究考虑地面干扰的飞行器非定常气动特性,童静等[115]基于滑移网格技术开展了地面效应的NACA0012翼型动态特性数值模拟。地面效应不仅对定常流场产生影响,更显著地影响了非定常气动力及力矩,近地高度越小,升力系数的迟滞环面积越小,而力矩系数的迟滞环变化不规律。地面效应干扰在飞行器非定常气动研究中应该引起重视。 数值离散方法研究是动态特性数值计算的重要环节。目前国内动态特性的计算大多采用二阶格式,而高精度、高分辨率格式可以较好地模拟以大范围分离为代表的、强非定常的非线性多尺度流动现象。赵云飞等[116]基于空间5阶精度格式WCNS(Weighted Compact Nonlinear Schemes)采用非定常Euler方程计算了NACA0012翼型强迫俯仰振动,研究了物理时间步长、子迭代收敛判据等因素对计算结果的影响。赵文文等[117]采用Van-Leer矢通量分裂格式(FVS)、ROE格式(FDS)、AUSMPW+格式、5阶精度WENO格式及高精度WNND格式对钝锥体俯仰阻尼导数进行了计算。分析认为差分格式之间不同的黏性分辨率是动导数结果差异的主要来源。采用高精度、高分辨率格式可以更好地处理复杂外形强非定常的非线性多尺度流动问题,是未来动态特性模拟技术研究的发展方向。 4.5自由振动方法 自由振动模拟方法是动导数的非定常时域求解的另一种重要方法。赵云飞[118]推导了非定常自由振动法确定动导数的计算公式。 图9是钝锥自由振动俯仰角时间历程曲线示例,曲线形态呈角振幅指数衰减。文献[118]通过提取波峰和波谷处的角振幅及周期T来计算动导数,该方法仅适用于小阻尼振幅衰减的情况。对振幅发散或者大阻尼的情况,可以通过Moore-Penrose广义逆方法求解任意位置的动导数,但计算精度还需做进一步的考察。 图9 钝锥自由俯仰振动动导数提取示意图Fig.9 Sketch showing extraction of dynamic derivatives of blunt cone free pitch vibration 与强迫振动法相比,自由振动法的优点是不存在频率相似问题,通过选取真实的惯量参数,自由振动法的振动频率与真实飞行情况相似度高。但自由振动法的缺点是辨识精度低、计算工作量比强迫振动法大、一般仅适合配平状态的动导数计算。此外该方法对交叉导数、交叉耦合导数和加速度导数的计算较为困难,所能辨识的动导数种类有限。 动导数常规计算方法是采用CFD模拟飞行器的微振幅强迫简谐振动。由于预测动导数需要计算与时间相关的动态非定常气动响应,非定常计算效率是CFD在动导数方面应用的瓶颈。强迫简谐振动的气动荷载在初始瞬时值衰变之后的变化具有周期性。频域计算利用动态非定常系统的周期性来获得动导数。该方法只需求解一个周期内几个时刻的瞬时流场,通过简单的后处理即可重建整个周期的非定常流动,对于长周期的非定常问题效率优势特别明显,从而获得了广泛关注和应用。时域仿真采用的频率受时间和空间分辨率的限制,但频域计算不存在这一问题。 常用的频域方法包括线性频域法和非线性频域法。谐波平衡(HB)法属于非线性频域法的一种类型,其计算精度和效率综合考虑具有较大的优势,因此是频域计算中应用最广泛的方法。经过十几年的发展,目前谐波平衡法主要有4种形式:直接谐波平衡法、时域谐波平衡法、频域谐波平衡法以及分裂域谐波平衡法。谐波平衡法考虑如下的周期性流动问题: (12) 式中:Ql,j和Rl,j分别为在网格点j上第l个守恒变量和第l个空间残差组分。将变量和空间离散后的残差项都可以表示为傅里叶级数的形式,代入到流动控制方程中,并利用正弦函数的正交性进行谐波平衡,得到频域上的谐波平衡方程为 (13) 式中:ω为圆频率;n为第n个谐波。 频域方法最初是因为涡轮机设计上的需要而被开发[119-120],此后被应用于飞行器气动力的求解[121-123]。Thomas等[124-131]应用时域谐波平衡法模拟翼型和F16机翼在跨声速流动时的极限环振动和颤振问题以及圆柱的绕流问题,并提出了一种新的稳定性技术来消除显式处理谐波源项引起的不稳定。Ekici等[132-135]应用高维时域谐波平衡法模拟直升机旋翼绕流问题并在多个基准频率下模拟多级涡轮机组的叶片绕流问题。斯坦福大学的McMullen等[136-139]利用频域谐波平衡方法数值模拟了一维管道流和圆柱绕流,并提出了一种迭代求解时间周期的方法,应用并成功模拟圆柱绕流的涡脱落问题和翼型的俯仰振荡问题,为对于事先不知道振荡频率的问题提供了一种求解方法。Mosahebi和Nadarajah[140]随后应用自适应谐波平衡法模拟了跨声速翼型俯仰振荡和圆柱绕流问题。Choi等[141]将时间谱方法应用于直升机旋翼运动,取得了较好的效果。谐波平衡法求解这种存在多个频率的情况,会出现稳定性问题,因此Guédeney等[142]提出时间样点不均匀分布的观点,并证明了其稳定性和可靠性。在动导数预测方面,Ronch等[143]对比了时间推进法、线性频域方法和谐波平衡法在数值预测动导数和消耗内存方面的能力。Hassan和Sicot[144]将谐波平衡法应用于动导数的快速预测。Murman等[145-146]将谐波平衡法应用于预测Finner及SDM(StandardDynamicModel)模型的动导数。 国内对谐波平衡法的研究较少。李道春和向锦武[147]应用谐波平衡法研究非线性二元机翼气动弹性。杜鹏程和宁方飞应用时域谐波平衡法模拟跨声风扇周向畸变流动[148],考查不同周期性边界条件对求解的影响,并采用预处理技术,将可压谐波平衡方程直接用于低速周期性流动的计算。许建华等[149]应用时域谐波平衡法模拟旋翼前飞绕流问题。杨小权等[150]应用时间谱方法模拟了俯仰翼型和机翼的强迫运动问题。谢立军等[151]采用时间谱方法对高超声速HBS标模和超声速Finner标模进行动导数计算。陈琦等采用谐波平衡法开展翼型和钝锥的非定常绕流模拟[152],并预测了带翼导弹的俯仰动导数[153]。 由于频域计算的数学简化,导致对非定常流动的计算精度远低于时域计算,当流动出现明显的非线性效应时其应用受到限制。图10给出了采用线性频域法计算的NACA0012翼型强迫简谐振动与时域计算的比较[154]。实线是时域(TimeDomain)计算结果,虚线是线性频域(LinearFrequencyDomain,LFD)法计算结果。线性频域法计算未能模拟出NACA0012振动时出现在两端处的非线性拐折。图11给出了不同外形的谐波平衡法与时域计算比较。Nr代表谐波平衡方法中的谐波数。从图中可以看出,无论是对于简单外形还是复杂外形,一个谐波对应的3个非定常流场样本均不足以精确模拟非定常振动出现的非线性气动力。与时域计算吻合一致的计算谐波数至少在2个以上。 Note: LFD—Linear frequency domain.图10 NACA0012翼型线性频域法与时域计算比较Fig.10 Comparison between NACA0012 airfoil linear frequency domain method and time-domain simulation 图11 谐波平衡法与时域计算比较Fig.11 Comparison between harmonic balance method and time-domain simulation 频域计算最大的特点是利用动态系统的周期性极大地减少非定常CFD仿真的计算开销。CFD时域仿真需要多个周期达到气动响应的谐振解,并且要达到时间上的精确求解必须采用小的时间步长来精确捕获流体运动,因此需要大量的计算开销[155-156]。而频域计算可以高效近似求解飞行器周期性的非定常小扰动条件下气动力,在减少计算开销的情况下估算动导数。图12是作者所在课题组针对类X-51内外流一体化外形双时间步方法时域计算与谐波平衡法的比较,图中CA为轴向力系数。内外流一体化外形半场网格量为2 000万,时域计算与谐波平衡法均采用18个CPU(IntelCorei7)进行并行计算。图中dt代表双时间步方法的无量纲时间步长,nsub代表内迭代步数。当时间步长取0.1,内迭代取20步时,双时间步法计算1.5个周期共5 000步的耗时约为48h,与谐波平衡法计算两万步基本达到收敛的用时相等,但此时双时间步方法的精度远低于谐波平衡法。随着内迭代步数的增加和时间步长的减小,二者达到同等精度时双时间步方法计算一个状态的耗时约为50天,是谐波平衡法计算时间的25倍。 图12 类X-51内外流一体化外形双时间步方法时域计算与谐波平衡法比较Fig.12 Comparison of time domain simulation of analogous X-51A-like hypersonic vehicle with dual time step method and that with harmonic balance method 图13 NACA0012强迫简谐振动频域法的计算效率Fig.13 Computational efficiency of NACA0012 forced harmonic vibration frequency-domain method 在对飞行稳定性问题进行概述的基础上,介绍了飞行器动导数数值模拟的国内外研究进展。对近年来主要的动导数计算方法进行了综述分析,结论显示: 1) 动导数的工程近似方法与CFD方法相比精度较低,但其最大的优势在于快捷高效。工程方法依赖于经验性,只适用于简单外形,不考虑边界层转捩、流动的分离和再附以及复杂背风区涡流情况下的小迎角线性范围。 2) 谐振摄动法和锥运动方法由于方法本身的局限性,对复杂外形和复杂流态的模拟能力有限,应用上存在诸多限制,工程实际中较少使用。 3) 准定常方法与非定常强迫振动方法的计算精度基本一致,是一种快速高效的动导数求解方法。但该方法仅适用于旋转导数计算。 4) 自由振动法的优点是振动频率与真实飞行情况相似度高。强迫振动的特点是适合不同状态的动导数计算,能够辨识的动导数种类丰富,对交叉导数、交叉耦合导数和加速度导数均有较好的模拟能力。因此目前采用强迫振动方法获得动导数是当前飞行品质和操稳特性研究中一种最理想、最现实的方式,且可靠性有望接近飞行试验。 5) 频域计算利用动态非定常系统的周期性来精确高效地获得动导数,获得了广泛关注和应用。谐波平衡法中谐波数Nr的选取需要综合考虑计算资源、计算精度与效率。 虽然近年来在非定常气动力计算、动导数辨识方法及非定常气动力建模等方面取得了较大进展,但为了更高效地获得不同类型的准确、可靠的动导数数据,仍有大量工作要做: 1) 非定常气动力的数学模型用于确定气动力所依赖的运动状态变量及其之间的数学关系。现代飞行器外形设计和运动方式比传统飞行器复杂,应进一步发展能够全面反映气动力对迎角的强烈非线性依赖关系、时间延迟效应、气动力的交叉耦合等特点的非定常气动力模型。 2) 动导数的计算需要综合考虑精度与效率。在目前CFD方法模拟效率不高的前提下,工程近似方法依然是飞行器型号设计初期满足动导数快速分析需求的重要手段。准定常计算方法和非定常频域计算方法作为非定常时域求解的简化近似方法,其适用范围及计算精度有待于深入研究。 3) 目前动导数的研究大多围绕绕定轴振动的组合导数,针对加速度导数和旋转导数的研究较少,对交叉导数和交叉耦合导数的预测也经验不足。如何准确可靠地预测这类动导数,仍有大量工作要做。 4) 目前针对工程复杂外形的动导数模拟研究较少,工程实际外形的非定常流场的准确模拟是动导数计算的重要基础。动态非定常条件下的激波诱导分离、旋涡运动与破裂以及它们之间的相互作用使得动导数的精确模拟是一件非常困难的工作。采用高精度、高分辨率格式可以更好地处理复杂外形强非定常的非线性多尺度流动问题,是未来动态特性模拟技术研究的发展方向。此外,针对工程问题中遇到的高温气体效应、稀薄气体效应、喷流影响等实际情况下的动导数计算还需做进一步深入的研究。 [1]刘伟. 细长机翼摇滚机理的非线性动力学分析及数值模拟方法研究[D]. 长沙: 国防科学技术大学, 2004: 20. LIU W. Nonlinear dynamics analysis for mechanism of slender wing rock and study of numerical simulation method[D]. Changsha: National University of Defense Technology, 2004: 20 (in Chinese). [2]杨小亮. 飞行器多自由度耦合摇滚运动数值模拟研究[D]. 长沙: 国防科学技术大学, 2012: 2. YANG X L. Numerical investigation of aircraft rock in multiple degrees of freedom[D]. Changsha: National University of Defense Technology, 2012: 2 (in Chinese). [3]CHAMBERS J R, HALL R M. Historical review of uncommanded lateral-directional motions at transonic conditions[J]. Journal of Aircraft, 2004, 41(3): 436-447. [4]WOODSON S H, GREEN B E, CHUNG J J, et al. Understanding abrupt wing stall with computational fluid dynamics[J]. Journal of Aircraft, 2005, 42(3): 578-585. [5]FORSYTHE J R, FREMAUX C M, HALL R M. Calculation of static and dynamic stability derivatives of the F/A-18E in abrupt wing stall using RANS and DES[M]//Computational Fluid Dynamics. Berlin: Springer, 2006: 537-542. [6]杨小亮, 刘伟, 吴天佐, 等. 细长三角翼滚转/侧滑耦合运动效应分析[J]. 空气动力学学报, 2014, 32(1): 1-7. YANG X L, LIU W, WU T Z, et al. Coupling mechanism analysis of a slender delta wing in combined free-roll and free-sideslip motion[J]. Acta Aerodynamica Sinica, 2014, 32(1): 1-7 (in Chinese). [7]BOYD T J M. One hundred years of G.H. Bryan’s stability in aviation[J]. Journal of Aeronautical History, 2011(4): 97-115. [8]NIELSEN J N. Missile aerodynamics[M]. New York: McGraw-Hill, 1960: 35. [9]贺国宏, 杨小亮, 赵海洋, 等. 高超声速弹头俯仰动态特性数值研究[J]. 兵工学报, 2009, 30(7): 862-866. HE G H, YANG X L, ZHAO H Y, et al. Numerical study of pitching dynamic characteristic for hypersonic missile[J]. Acta Armamentarii, 2009, 30(7): 862-866 (in Chinese). [10]牟斌, 刘伟, 瞿章华. 球锥体高超声速绕流的俯仰阻尼导数的数值计算[J]. 国防科技大学学报, 2000, 22(4): 5-10. MOU B, LIU W, QU Z H. Numerical calculation of damping-in-pitch derivatives for hypersonic flowover sphere-cone bodies[J]. Journal of National University of Defense Technology, 2000, 22(4): 5-10 (in Chinese). [11]伍开元. 民机空难相关非定常气动力问题研究[J]. 流体力学实验与测量, 2003, 17(2): 1-9. WU K Y. Unsteady aerodynamics in fatal accidents[J]. Experiments and Measurements in Fluid Mechanics, 2003, 17(2): 1-9 (in Chinese). [12]童秉纲, 陈强. 关于非定常空气动力学[J]. 力学进展, 1983(4): 377-394. TONG B G, CHEN Q. Some remarks on unsteady aerodynamics[J]. Advances in Mechanics, 1983(4): 377-394 (in Chinese). [13]BRYAN G H, WILLIAMS W E. The longitudinal stability of aerial gliders[J]. Proceedings of the Royal Society of London, 1904, 73(488-496): 100-116. [14]BRYAN G H. Stability in aviation: An introduction to dynamical stability as applied to the motions of aeroplanes[J]. Nature, 1912, 88(25): 406-407. [15]ETKIN B, REID L D. Dynamics of flight: Stability and control[M]. New York: Wiley, 1996: 107. [16]ETKIN B. Dynamics of atmospheric flight[M]. New York: Dover Publications, 2012: 125. [17]TOBAK M, SCHIFF L B. Aerodynamic mathematical modeling-basic concepts[J]. AGARD Lecture Series, 1981, 77(114): 1-32. [18]TOBAK M, SCHIFF L B. On the formulation of the aerodynamic characteristics in aircraft dynamics: NASA TR R-456[R]. Washington, D.C.: NASA, 1976. [19]VOLTERRA V. Theory of functionals and of integral and integro-differential equations[M]. New York: Dover Publications, 2005: 25. [20]TOBAK M, SCHIFF L B. The role of time-history effects in the formulation of the aerodynamics of aircraft dynamics: NASA TM 78471[R]. Washington, D.C.: NASA, 1978. [21]任玉新, 刘秋生, 沈孟育. 飞行器动态稳定性参数的数值计算方法[J]. 空气动力学学报, 1996, 14(2): 117-126. REN Y X, LIU Q S, SHEN M Y. A numerical method for evaluating aerodynamic stability parameters of vehicles[J]. Acta Aerodynamica Sinica, 1996, 14(2): 117-126 (in Chinese). [22]COWLEY W L, GLAUERT H. The effect of the lag of the downwash on the longitudinal stability of an aeroplane and on the rotary derivative Mq[M]. London: HM Stationery Office, 1921: 25-33. [23]KLEIN V, MORELLI E A. Aircraft system identification: Theory and practice[M]. Reston: AIAA, 2006: 132. [24]BOLSTER C. Effect of slipstream on the longitudinal stability of a low wing monoplane[J]. Journal of the Aeronautical Sciences, 2012, 4(10): 411-416. [25]刘绪, 刘伟, 周云龙, 等. 吸气式内外流一体化飞行器动导数数值模拟[J]. 空气动力学学报, 2015, 33(2): 147-155. LIU X, LIU W, ZHOU Y L, et al. Numerical simulation of dynamic derivatives for air-breathing hypersonic vehicle[J]. Acta Aerodynamica Sinica, 2015, 33(2): 147-155 (in Chinese). [26]ADAMS M C. Slender-body theory-review and extension[J]. Journal of the Aeronautical Sciences, 2012, 20(2): 85-98. [27]KÜSSNER H. A general method for solving problems of the unsteady lifting surface theory in the subsonic range[J]. Journal of the Aeronautical Sciences, 1954, 21(1): 17-26. [28]ERICSSON L E. Generalized unsteady embedded Newtonian flow[J]. Journal of Spacecraft and Rockets, 1975, 12(12): 718-726. [29]HUI W H. Stability of oscillating wedges and caret wings in hypersonic and supersonic flows[J]. AIAA Journal, 1969, 7(8): 1524-1530. [30]ORLIK-RÜCKEMANN K. Dynamic stability parameters[C]//AGARD Conference Proceedings No. 235. New York: AGARD, 1978. [31]任玉新. 基于敏感性分析的飞行器动导数计算方法[C]//空气动力学前沿研究学术研讨会. 北京: 中国空气动力学会, 2003: 390-396. REN Y X. Calculation method of dynamic derivatives based on sensitivity analysis[C]//Proceedings of the Academic Seminar on the Forefront of Aerodynamics. Beijing: Chinese Aerodynamics Research Society, 2003: 390-396 (in Chinese). [32]任玉新, 雷国东. 飞行器稳定性参数的理论与计算方法[C]//中国力学学会学术大会. 北京: 中国力学学会, 2009: 231-345. REN Y X, LEI G D. Theory and calculation method of aircraft stability parameter[C]//Proceedings of the Chinese Conference of Theoretical and Applied Mechanics. Beijing: The Chinese Society of Theoretical and Applied Mechanics, 2009: 231-245 (in Chinese). [33]郭晨曦, 任玉新. 基于敏感性分析方法计算三维钝锥的气动稳定性导数[C]//中国力学学会学术大会. 北京: 中国力学学会, 2013: 182. GUO C X, REN Y X. Based on sensitivity analysis method for calculating dynamic derivatives of blunt cone[C]//Proceedings of the Chinese Conference of Theoretical and Applied Mechanics. Beijing: The Chinese Society of Theoretical and Applied Mechanics, 2013: 182 (in Chinese). [34]刘伟, 牟斌. 高超声速滚转阻尼导数数值模拟[J]. 飞行力学, 2000, 18(2): 27-29. LIU W, MOU B. Numerical simulation of damping-in-roll derivatives of blunt cone for hypersonic flow[J]. Flight Mechanics, 2000, 18(2): 27-29 (in Chinese). [35]刘伟, 瞿章华. 强迫振动法求解偏航阻尼导数[J]. 推进技术, 1998, 19(3): 30-32. LIU W, QU Z H. Calculation of damping-in-yaw derivatives by forced oscllation method[J]. Journal of Propulsion Technology, 1998, 19(3): 30-32 (in Chinese). [36]刘伟, 牟斌. 类升力体俯仰阻尼特性数值研究[C]//第十届全国计算流体力学会议. 北京: 中国力学学会, 2000: 381-386. LIU W, MOU B. Numerical study of damping-in-pitch characteristics for liftbody-type[C]//Proceedings of the Tenth National Conference for Computational Fluid Dynamics. Beijing: The Chinese Society of Theoretical and Applied Mechanics, 2000: 381-386 (in Chinese). [37]袁先旭, 张涵信, 谢昱飞. 基于CFD方法的俯仰静、动导数数值计算[J]. 空气动力学学报, 2005, 23(4): 458-463. YUAN X X, ZHANG H X, XIE Y F. The pitching static/dynamic derivatives computation based on CFD methods[J]. Acta Aerodynamica Sinica, 2005, 23(4): 458-463 (in Chinese). [38]袁先旭, 张涵信, 谢昱飞. 基于非定常流场数值模拟的俯仰阻尼导数计算方法[C]//近代空气动力学研讨会. 北京: 中国空气动力学会, 2005: 301-309. YUAN X X, ZHANG H X, XIE Y F. Pitch damping derivative calculation method based on unsteady flow field numerical simulation[C]//Proceedings of the Modern Aerodynamics Conference. Beijing: Chinese Aerodynamics Research Society, 2005: 301-309 (in Chinese). [39]袁先旭, 谢昱飞, 陈亮中, 等. 飞行器静稳定性导数的非定常数值模拟研究[C]//中国力学学会学术大会. 北京: 中国力学学会, 2013: 181. YUAN X X, XIE Y F, CHEN L Z, et al. Study on the unsteady numerical simulation of the static stability of the aircraft[C]//Proceedings of the Chinese Conference of Theoretical and Applied Mechanics. Beijing: The Chinese Society of Theoretical and Applied Mechanics, 2013: 181 (in Chinese). [40]袁先旭, 陈琦, 何琨, 等. 再入飞行器俯仰动态失稳的分叉理论与计算分析[J]. 空气动力学学报, 2015, 33(2): 162-169. YUAN X X, CHEN Q, HE K, et al. Dynamic destabilization analysis of the reentry vehicles using bifurcation theory and unsteady numerical simulation[J]. Acta Aerodynamica Sinica, 2015, 33(2): 162-169 (in Chinese). [41]史爱明, 杨永年, 叶正寅. 结合CFD技术的跨音速动导数计算方法研究[J]. 西北工业大学学报, 2008, 26(1): 11-14. SHI A M, YANG Y N, YE Z Y. A more accurate method for calculating transonic dynamic derivatives (TDDs) using present state-of-the-art CFD[J]. Journal of Northwestern Polytechnical University, 2008, 26(1): 11-14 (in Chinese). [42]卢学成, 叶正寅, 张伟伟. 超音速、高超音速飞行器动导数的高效计算方法[J]. 航空计算技术, 2008, 38(3): 28-31. LU X C, YE Z Y, ZHANG W W. A high efficient method for computing dynamic derivatives of supersonic/hypersonic aircraft[J]. Aeronautical Computing Technique, 2008, 38(3): 28-31 (in Chinese). [43]陶洋, 范召林, 赵忠良. 基于CFD的带控制舵导弹的动导数计算[J]. 航空动力学报, 2010, 25(1): 102-106. TAO Y, FAN Z L, ZHAO Z L. Predictions of dynamic damping coefficients of basic finner based on CFD[J]. Journal of Aerospace Power, 2010, 25(1): 102-106 (in Chinese). [44]陶洋, 袁先旭, 范召林, 等. 方形截面导弹摇滚特性数值研究[J]. 空气动力学学报, 2010, 28(3): 285-290. TAO Y, YUAN X X, FAN Z L, et al. Numerical investigation of dynamic behavior of square section missile in roll at high incidence[J]. Acta Aerodynamica Sinica, 2010, 28(3): 285-290 (in Chinese). [45]范晶晶, 阎超, 李跃军. 飞行器大迎角下俯仰静、动导数的数值计算[J]. 航空学报, 2009, 30(10): 1846-1850. FAN J J, YAN C, LI Y J. Computation of vehicle pitching static and dynamic derivatives at high angles of attack[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(10): 1846-1850 (in Chinese). [46]陈东阳, Laith K. ABBAS, 芮筱亭. 旋转弹箭气动导数与气动热仿真计算[J]. 计算机仿真, 2014(5): 26-30. CHEN D Y, ABBAS L K, RUI X T. Aerodynamic derivative and aerodynamic heating simulation and computation of spinning vehicle[J]. Computer Simulation, 2014(5): 26-30 (in Chinese). [47]陈东阳. 超音速旋转弹箭气动特性及流固耦合计算分析[D]. 南京: 南京理工大学, 2014: 8-34. CHEN D Y. Aerodynamic characteristics and fluid-structure interaction computations and analysis of supersonic spinning flying vehicle[D]. Nanjing: Nanjing University of Science and Technology, 2014: 8-34 (in Chinese). [48]黄龙太, 王红伟, 姜琬. 基于CFD动网格技术的飞艇动导数计算方法[J]. 航空计算技术, 2013(6): 66-68. HANG L T, WANG H W, JIANG W. A method of calculating airship dynamic derivative based on CFD dynamic mesh technique[J]. Aeronautical Computer Technique, 2013(6): 66-68 (in Chinese). [49]陈春鹏, 杨康智, 王莉萍. 飞机气动力工程估算的程序化实现方法[J]. 科技创新与应用, 2014(6): 26-27. CHEN C P, YANG K Z, WANG L P. Aircraft aerodynamics engineering estimation of program implementation[J]. Technology Innovation and Application, 2014(6): 26-27 (in Chinese). [50]蒋胜矩, 刘玉琴, 党明利. 基于定常NS方程的飞行器滚转阻尼力矩系数导数计算方法[J]. 弹箭与制导学报, 2008, 28(1): 180-182. JIANG S J, LIU Y Q, DANG M L. A calculation method of aircraft roll-damping moment coefficient derivative based on steady NS equation[J]. Journal of Projectiles Rockets Missiles and Guidance, 2008, 28(1): 180-182 (in Chinese). [51]孙智伟, 程泽荫, 白俊强, 等. 基于准定常的飞行器动导数的高效计算方法[J]. 飞行力学, 2010, 28(2): 28-30. SUN Z W, CHENG Z Y, BAI J Q, et al. A high efficient method for computing dynamic derivatives of aircraft based on quasi-steady CFD method[J]. Flight Dynamics, 2010, 28(2): 28-30 (in Chinese). [52]HALL K C, EKICI K, THOMAS J P, et al. Harmonic balance methods applied to computational fluid dynamics problems[J]. International Journal of Computational Fluid Dynamics, 2013, 27(2): 52-67. [53]王勇献, 张理论, 车永刚, 等. 结构网格CFD应用程序在天河超级计算机上的高效并行与优化[J]. 电子学报, 2015, 43(1): 36-44. WANG Y X, ZHANG L L, CHE Y G, et al. Efficient parallel computing and performance tuning for multi-block structured grid CFD applications on Tianhe supercomputer[J]. Acta Electronica Sinica, 2015, 43(1): 36-44 (in Chinese). [54]阎超. 计算流体力学方法及应用[M]. 北京: 北京航空航天大学出版社, 2006: 152-157. YAN C. Computational fluid dynamics method and its application[M]. Beijing: Beihang University Press, 2006: 152-157 (in Chinese). [55]GLAZ B, LIU L, FRIEDMANN P P. Reduced-order nonlinear unsteady aerodynamic modeling using a surrogate-based recurrence framework[J]. AIAA Journal, 2010, 48(10): 2418-2429. [56]ROSENBAUM B, SCHULZ V. Response surface methods for efficient aerodynamic surrogate models, Vol.123: Computational flight testing[M]. Berlin: Springer, 2013: 113-129. [57]刘绪. 高超声速内外流一体化飞行器动态特性研究[D]. 长沙: 国防科学技术大学, 2011: 35-49. LIU X. Investigation of dynamic characteristics of hypersonic airframe/propulsion integrative vehicle[D]. Changsha: National University of Defense Technology, 2011: 35-49 (in Chinese). [58]叶川, 马东立. 带翼潜航器动力学建模及动稳定性[J]. 北京航空航天大学学报, 2013, 39(9): 1137-1143. YE C, MA D L. Dynamic modeling and stability analysis for underwater craft with wing[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(9): 1137-1143 (in Chinese). [59]马东立, 叶川. 升力浮力复合型飞艇动导数分析[J]. 航空动力学报, 2013, 28(5): 1074-1080. MA D L, YE C. Dynamic derivative analysis for hybrid airship incorporating lift and buoyancy[J]. Journal of Aerospace Power, 2013, 28(5): 1074-1080 (in Chinese). [60]米百刚, 詹浩, 王斑. 基于刚性动网格技术的动导数数值模拟[J]. 航空动力学报, 2014, 29(11): 2659-2664. MI B G, ZHAN H, WANG B. Numerical simulation of dynamic derivatives based on rigid moving mesh technique[J]. Journal of Aerospace Power, 2014, 29(11): 2659-2664 (in Chinese). [61]席柯, 阎超, 黄宇, 等. 俯仰阻尼导数分量的CFD数值模拟[J]. 北京航空航天大学学报, 2015, 41(2): 222-227. XI K, YAN C, HUANG Y, et al. Numerical simulation of individual components of pitch-damping coefficient sum[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(2): 222-227 (in Chinese). [62]叶川, 马东立. 利用CFD技术计算飞行器动导数[J]. 北京航空航天大学学报, 2013, 39(2): 196-200. YE C, MA D L. Aircraft dynamic derivatives calculation using CFD techniques[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(2): 196-200 (in Chinese). [63]THEODORSEN T, GARRICK I. General potential theory of arbitrary wing sections[M]. New York: US Government Printing Office,1933: 77-80. [64]VUKELICH S R, WILLIAMS J E. The USAF stability and control digital DATCOM: AFFDL-TR-79-3032[R]. Ohio: WP-AFB, 1979. [65]SCHUMMER J. A conceptual approach[J]. HYLE-International Journal for Philosophy of Chemistry, 1998, 4(2): 129-162. [66]ROSKAM J. Airplane design: Part 2—Preliminary configuration design and integration of the propulsion system[M]. Lawrence: DAR Corporation, 1985: 86. [67]WEINACHT P. Navier-Stokes predictions of the individual components of the pitch-damping sum[J]. Journal of Spacecraft and Rockets, 1998, 35(5): 598-605. [68]EAST R A, HUTT G R. Comparison of predictions and experimental data for hypersonic pitching motion stability[J]. Journal of Spacecraft and Rockets, 1988, 25(3): 225-233. [69]赫姆施. 战术导弹空气动力学[M]. 北京: 宇航出版社, 1999: 57. HEMSCH M J. Tactical missile aerodynamics[M]. Beijing: Astronautics Press, 1999: 57 (in Chinese). [70]瞿章华. 高超音速飞行器空气动力学[M]. 长沙: 国防科技大学出版社, 1999: 105. QU Z H. Hypersonic vehicle aerodynamics[M]. Changsha: National University of Defence Technology Press, 1999: 105 (in Chinese). [71]TONG B G, HUI W. Unsteady embedded Newton-Busemann flow theory[J]. Journal of Spacecraft and Rockets, 1986, 23: 129-135. [72]飞机设计手册总编委会. 飞机设计手册: 气动设计[M]. 北京: 航空工业出版社, 2002: 252. Aircraft Design Manual Editorial Board. Aircraft design manual: Aerodynamic design[M]. Beijing: Aviation Industry Press, 2002: 252 (in Chinese). [73]熊海泉, 刘昶, 郑本武. 飞机飞行动力学[M]. 北京: 航空工业出版社, 1990: 75. XIONG H Q, LIU C, ZHEN B W. Aircraft flight dynamics[M]. Beijing: Aviation Industry Press, 1990: 75 (in Chinese). [74]ROSKAM J. Airplane design Part VI: Preliminary calculation of aerodynamic, thrust and power characteristics[M]. Kansas: Aviation and Engineering Corporation, 1990: 253. [75]TOBAK M, WEHREND W R. Stability derivatives of cones at supersonic speeds: NACA TN 3788[R]. Washington, D.C.: NACA, 1956. [76]BUSEMANN A. Handwörterbuch der naturwissenschaften, IV, Flussigkeits-mnd garbewegung[M]. Zweite Auflage. Jena: Gustav Fische, 1933: 12-55. BUSEMANN A. Handbook of natural sciences, IV, Liquid and garbewegung[M]. 2nd ed. Jena: Gustav Fischer, 1933: 12-55 (in German). [77]MESSITER A F. Lift of slender delta wings according to newtonian theory[J]. AIAA Journal, 1963, 1(4): 794-802. [78]MAHOOD G, HUI W. Remarks on unsteady Newtonian flow theory[J]. Aeronautical Quarterly, 1976, 27(1): 66-74. [79]HUI W, TOBAK M. Unsteady Newton-Busemann flow theory. Part 2: Bodies of revolution[J]. AIAA Journal, 1981, 19(10): 1272-1273. [80]SEIFF A. Secondary flow fields embedded in hypersonic shock layers: NASA TN D-1304[R]. Washington, D.C.: NASA,1962. [81]ERICSSON L E. Unsteady aerodynamics of an ablating flared body of revolution including effect of entropy gradient[J]. AIAA Journal, 1968, 6(5): 2395-2401. [82]ERICSSON L E. Unsteady embedded Newtonian flow (as basis for nose bluntness effect on aerodynamics of hypersonic slender bodies)[J]. Astronautica Acta, 1973, 18(3): 309-330. [83]刘伟, 沈清. 钝倒锥体动导数数值工程模拟[J]. 国防科技大学学报, 1998, 20(1): 5-8. LIU W, SHEN Q. Numerical and analytic simulation of the dynamic stability derivative of blunt cone[J]. Journal of National University of Defense Technology, 1998, 20(1): 5-8 (in Chinese). [84]VAN DYKE M D. A study of second-order supersonic flow theory[J]. Technical Report Archive & Image Library, 1952, 9(1): 1081-1125. [85]LIGHTHILL M J. Oscillating airfoils at high Mach number[J]. Journal of the Aeronauticalences, 1953, 20(6): 402-406. [86]陈劲松. 超声速和高超声速机翼俯仰导数——当地流活塞理论解法[J]. 空气动力学学报, 1991, 9(4): 469-476. CHEN J S. Pitching derivatives of wing in supersonic and hypersonic stream-method for local flow piston theory[J]. Acta Arodynamica Sinica, 1991, 9(4): 469-476 (in Chinese). [87]张伟伟, 史爱民, 王刚, 等. 结合定常CFD技术的当地流活塞理论[C]//第十二届全国计算流体力学会议. 北京: 中国力学学会, 2004: 371-375. ZHANG W W, SHI A M, WANG G, et al. On determining unsteady aerodynamic loads accurately and efficiently[C]//Proceedings of the Twelfth National Conference for Computational Fluid Dynamics. Beijing: The Chinese Society of Theoretical and Applied Mechanics, 2004: 371-375 (in Chinese) [88]ZHANG W W, YE Z Y, ZHANG C A, et al. Supersonic flutter analysis based on a local piston theory[J]. AIAA Journal, 2009, 47(10): 2321-2328. [89]刘溢浪, 张伟伟, 田八林, 等. 一种超音速高超音速动导数的高效计算方法[J]. 西北工业大学学报, 2013, 31(5): 824-828. LIU Y L, ZHANG W W, TIAN B L, et al. Effectively calculating supersonic and hypersonic dynamic derivatives[J]. Journal of Northwestern Polytechnical University, 2013, 31(5): 824-828 (in Chinese). [90]HUI W H. Exact theory for the stability of an oscillating wedge in hypersonic and supersonic flows[D]. Southampton: University of Southampton, 1967: 205. [91]刘伟, 赵海洋, 杨小亮. 飞行器动态气动特性数值模拟方法[M]. 长沙: 国防科技大学出版社, 2015: 172. LIU W, ZHAO H Y, YANG X L. Numerical simulation method for aerodynamic characteristics of aircraft[M]. Changsha: National University of Defense Technology Press, 2015: 172 (in Chinese). [92]HUI W H, TOBAK M. Bifurcation analysis of aircraft pitching motions about large mean angles of attack[J]. Journal of Guidance, Control, and Dynamics, 1984, 7(1): 113-122. [93]HUI W H, VAN ROESSEL H J. Transient motion of a hypersonic wedge, including time history effects[J]. Journal of Guidance, Control, and Dynamics, 1986, 9(2): 205-212. [94]刘秋生, 沈孟育. 球锥俯仰阻尼导数的数值计算[J]. 空气动力学学报, 1995, 13(2): 132-142. LIU Q S, SHEN M Y. Calculation of damping-in-pitch derivatives of sphere-cone bodies[J]. Acta Aerodynamica Sinica, 1995, 13(2): 132-142 (in Chinese). [95]张才文. 超高超声速机翼俯仰导数的欧拉方程摄动解法[J]. 空气动力学学报, 1997, 15(3): 400-405. ZHANG C W. Pitching stability derivatives of wing in supersonic and hypersonic flows-perturbation method for Euler equation[J]. Acta Aerodynamica Sinica, 1997, 15(3): 400-405 (in Chinese). [96]刘伟, 张鲁民. 钝体俯仰阻尼导数数值计算[J]. 空气动力学学报, 1997, 15(4): 427-435. LIU W, ZHANG L M. Numerical calculation of damping-in-pitch derivatives of blunt body[J]. Acta Aerodynamica Sinica, 1997, 15(4): 427-435 (in Chinese). [97]刘伟, 张鲁民. 谐振摄动法求解钝体俯仰阻尼导数[C]//第八届全国计算流体力学会议. 北京: 中国力学学会, 1996: 297-301. LIU W, ZHANG L M. Resonant perturbation method for pitch damping derivatives of bluff body[C]//Proceedings of the Eighth National Conference for Computational Fluid Dynamics. Beijing: The Chinese Society of Theoretical and Applied Mechanics, 1996: 297-301 (in Chinese). [98]TOBAK M, SCHIFF L B. Generalized formulation of nonlinear pitch-yaw-roll coupling: Part I—Nonaxisymmetric bodies[J]. AIAA Journal, 1975, 13(3): 323-326. [99]SCHIFF L B. Nonlinear aerodynamics of bodies in coning motion[J]. AIAA Journal, 1972, 10(11): 1517-1522. [100]WEINACHT P, STUREK W B, SCHIFF L B. Navier-Stokes predictions of pitch-damping for axisymmetric shell using steady coning motion: ARL-TR-575[R]. Aberdeen Proving Ground, MD: U.S. Army Research Laboratory, 1994. [101]WEINACHT P, STUREK W B. Computation of the roll characteristics of a finned projectile[J]. Journal of Spacecraft and Rockets, 1996, 33(6): 769-775. [102]DESPIRITO J, SILTON S I, WEINACHT P. Navier-Stokes predictions of dynamic stability derivatives: Evaluation of steady-state methods[J]. Journal of Spacecraft and Rockets, 2009, 46(6): 1142-1154. [103]张一帆, 李中武, 姚冰, 等. F12全机动态特性数值模拟[J]. 航空计算技术, 2015(2): 22-25. ZHANG Y F, LI Z W, YAO B, et al. Dynamic derivative simulation of F12 aircraft configuration[J]. Aeronautical Computer Technique, 2015(2): 22-25 (in Chinese). [104]米百刚, 詹浩, 朱军. 基于CFD数值仿真技术的飞行器动导数计算[J]. 空气动力学学报, 2014, 32(6): 834-839. MI B G, ZHAN H, ZHU J. Calculation of dynamic derivatives for aircraft based on CFD technique[J]. Acta Aerodynamica Sinica, 2014, 32(6): 834-839 (in Chinese). [105]米百刚, 詹浩, 朱军. 基于准定常假设的飞行器滚转动导数数值模拟[J]. 弹箭与制导学报, 2013, 33(3): 21-24. MI B G, ZHAN H, ZHU J. A calculation method of rolling dynamic derivatives based on quasi-steady assumption[J]. Journal of Projectiles Rockets Missiles and Guidance, 2013, 33(3): 21-24 (in Chinese). [106]牟斌, 刘伟, 瞿章华. 倒锥体高超声速滚转阻尼导数数值模拟[C]//第十届全国高超声速气动力(热)学术交流会. 北京: 中国空气动力学会, 1999: 20-24. MOU B, LIU W, QU Z H. Numerical simulation of hypersonic cone roll damping derivative[C]//Proceedings of the National Hypersonic Aerodynamics (Heating) Conference. Beijing: Chinese Aerodynamics Research Society, 1999: 20-24 (in Chinese). [107]BOELENS O, BADCOCK K, ELMILGUI A, et al. Comparison of measured and block structured simulation results for the F-16XL aircraft[J]. Journal of Aircraft, 2009, 46(2): 377-384. [108]任玉新. 气动稳定性导数理论与计算方法[D]. 北京: 清华大学, 1992: 23-57. REN Y X. Theory and calculation method of aerodynamic stability derivatives[D]. Beijing: Tsinghua University, 1992: 23-57 (in Chinese). [109]孙涛, 高正红, 黄江涛. 基于 CFD 的动导数计算与减缩频率影响分析[J]. 飞行力学, 2011, 29(4): 15-18. SUN T, GAO Z H, HUANG J T. Identify of aircraft dynamic derivatives based on CFD technology and analysis of reduce frequency[J]. Flight Dynamics, 2011, 29(4): 15-18 (in Chinese). [110]WHEELER A J, GANJI A R, KRISHNAN V V, et al. Introduction to engineering experimentation[M]. Upper Saddle River, NJ: Prentice Hall, 1996: 96. [111]刘绪, 赵云飞, 王东方, 等. 高超声速内外流一体化飞行器动态特性[J]. 弹道学报, 2013, 25(3): 38-43. LIU X, ZHAO Y F, WANG D F, et al. Dynamic characteristics of hypersonic integrative vehicle with internal and external flow[J]. Journal of Ballistics, 2013, 25(3): 38-43 (in Chinese). [112]BRANDON J M, FOSTER J V. Recent dynamic measurements and considerations for aerodynamic modeling of fighter airplane configurations: AIAA-1998-4447[R]. Reston: AIAA, 1998. [113]刘伟, 刘君, 柳军. 平衡气体效应对飞行器动态特性的影响研究[J]. 飞行力学, 2004, 22(4): 65-68. LIU W, LIU J, LIU J. Investigation of equilibrium gas effect on dynamic characteristic of aerocraft[J]. Flight Dynamics, 2004, 22(4): 65-68 (in Chinese). [114]赵文文, 陈伟芳, 邵纯, 等. 考虑多种物理效应的钝锥俯仰稳定性参数影响分析[J]. 空气动力学学报, 2013, 31(4): 442-448. ZHAO W W, CHEN W F, SHAO C, et al. The research on the influence of hypersonic blunt cone pitching dynamic derivatives considering different physical effects[J]. Acta Aerodynamica Sinica, 2013, 31(4): 442-448 (in Chinese). [115]童静, 夏露, 詹浩, 等. 考虑地面效应的翼型动态特性数值模拟[J]. 航空计算技术, 2014(3): 88-91. TONG J, XIA L, ZHAN H, et al. Numerical simulation on unsteady flow around an oscillating airfoil with ground effect[J]. Aeronautical Computer Technique, 2014(3): 88-91 (in Chinese). [116]赵云飞, 刘绪, 涂国华, 等. 非定常Euler方程数值计算中高精度格式应用[J]. 国防科技大学学报, 2012, 34(3): 12-16. ZHAO Y F, LIU X, TU G H, et al. High-accuracy numerical method applied to calculate unsteady Euler equations[J]. Journal of National University of Defense Technology, 2012, 34(3): 12-16 (in Chinese). [117]赵文文, 陈伟芳, 邵纯, 等. 高超声速钝锥体俯仰阻尼导数影响因素分析[J]. 国防科技大学学报, 2013, 35(1): 43-47. ZHAO W W, CHEN W F, SHAO C, et al. The research on the influence of hypersonic blunt cone pitching dynamic derivatives calculation[J]. Journal of National University of Defense Technology, 2013, 35(1): 43-47 (in Chinese). [118]赵云飞. 高精度格式在非定常流动中的应用研究[D]. 长沙: 国防科学技术大学, 2010: 105-121. ZHAO Y F. Application studies of high-order accurate schemes to unsteady flows[D]. Changsha: National University of Defense Technology, 2010: 105-121 (in Chinese). [119]CLARK W S, HALL K C. A time-linearized Navier-Stokes analysis of stall flutter[J]. Journal of Turbomachinery, 2000, 122(3): 467-476. [120]VAN DER WEIDE E, GOPINATH A, JAMESON A. Turbomachinery applications with the time spectral method: AIAA-2005-4905[R]. Reston: AIAA, 2005. [121]DUFOUR G, SICOT F, PUIGT G, et al. Contrasting the harmonic balance and linearized methods for oscillating-flap simulations[J]. AIAA Journal, 2010, 48(4): 788-797. [122]BLANC F, ROUX F X, JOUHAUD J C. Harmonic-balance-based code-coupling algorithm for aeroelastic systems subjected to forced excitation[J]. AIAA Journal, 2010, 48(11): 2472-2481. [123]PECHLOFF A N, LASCHKA B. Small disturbance Navier-Stokes method: Efficient tool for predicting unsteady air loads[J]. Journal of Aircraft, 2006, 43(1): 17-29. [124]THOMAS J P, DOWELL E H, HALL K C. Nonlinear inviscid aerodynamic effects on transonic divergence, flutter, and limit-cycle oscillations[J]. AIAA Journal, 2002, 40(4): 638-646. [125]THOMAS J, DOWELL E, HALL K, et al. Modeling limit cycle oscillation behavior of the F-16 fighter using a harmonic balance approach[C]//Proceedings of the 45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. Reston: AIAA, 2004: 297-305. [126]THOMAS J P, DOWELL E H, HALL K C. Modeling viscous transonic limit cycle oscillation behavior using a harmonic balance approach[J]. Journal of Aircraft, 2004, 41(6): 1266-1274. [127]THOMAS J P, DOWELL E H, HALL K C, et al. Further investigation of modeling limit cycle oscillation behavior of the F-16 fighter using a harmonic balance approach: AIAA-2005-1917[R]. Reston: AIAA, 2005. [128]HALL K C, THOMAS J P, DOWELL E H. Proper orthogonal decomposition technique for transonic unsteady aerodynamic flows[J]. AIAA Journal, 2000, 38(10): 1853-1862. [129]THOMAS J P, CUSTER C H, DOWELL E H, et al. Unsteady flow computation using a harmonic balance approach implemented about the OVERFLOW 2 flow solver[C]//Proceedings of the 19th AIAA Computational Fluid Dynamics Conference, Computational Fluid Dynamics Conference. Reston: AIAA, 2009: 308-321. [130]THOMAS J P, CUSTER C H, DOWEL E H, et al. Compact implementation strategy for a harmonic balance method within implicit flow solvers[J]. AIAA Journal, 2013, 51(6): 1374-1381. [131]SPIKER M A, THOMAS J P, KIELB R E, et al. Modeling cylinder flow vortex shedding with enforced motion using a harmonic balance approach: AIAA-2006-1965[R]. Reston: AIAA, 2006. [132]EKICI K, HALL K C. Nonlinear analysis of unsteady flows in multistage turbomachines using harmonic balance[J]. AIAA Journal, 2007, 45(5): 1047-1057. [133]EKICI K, HALL K C. Nonlinear frequency-domain analysis of unsteady flows in turbomachinery with multiple excitation frequencies[J]. AIAA Journal, 2008, 46(8): 1912-1920. [134]EKICI K, HALL K C, DOWELL E H. Computationally fast harmonic balance methods for unsteady aerodynamic predictions of helicopter rotors[J]. Journal of Computational Physics, 2008, 227(12): 6206-6225. [135]HUANG H, EKICI K. Stabilization of high-dimensional harmonic balance solvers using time spectral viscosity[J]. AIAA Journal, 2014, 52(8): 1784-1794. [136]ALONSO J J, MCMULLEN M, JAMESON A. Acceleration of convergence to a periodic steady state in turbomachinery flows[C]//AIAA 39th Aerospace Sciences Meeting and Exhibit, Aerospace Sciences Meetings. Reston: AIAA, 2001: 58-69. [137]MCMULLEN M, JAMESON A, ALONSO J. Application of a non-linear frequency domain solver to the Euler and Navier-Stokes equations: AIAA-2002-0120[R]. Reston: AIAA, 2002. [138]MCMULLEN M, JAMESON A. The computational efficiency of non-linear frequency domain methods[J]. Journal of Computational Physics, 2005, 212(2): 637-661. [139]MCMULLEN M, JAMESON A, ALONSO J. Demonstration of nonlinear frequency domain methods[J]. AIAA Journal, 2006, 44(7): 1428-1435. [140]MOSAHEBI A, NADARAJAH S. An adaptive non-linear frequency domain method for viscous periodic steady state flows[C]//Proceedings of the 48th Aerospace Sciences Meeting and Exhibit, Aerospace Sciences Meetings. Reston: AIAA, 2010: 152-161. [141]CHOI S, LEE K, POTSDAM M M, et al. Helicopter rotor design using a time-spectral and adjoint-based method[J]. Journal of Aircraft, 2014, 51(2): 412-423. [142]GUÉDENEY T, GOMAR A, GALLARD F, et al. Non-uniform time sampling for multiple-frequency harmonic balance computations[J]. Journal of Computational Physics, 2012, 236(2): 317-345. [143]RONCH D A, MCCRACKEN A J, BADCOCK K J, et al. Linear frequency domain and harmonic balance predictions of dynamic derivatives[J]. Journal of Aircraft, 2013, 50(3): 694-707. [144]HASSAN D, SICOT F. A time-domain harmonic balance method for dynamic derivatives predictions[C]//49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Aerospace Sciences Meetings. Reston: AIAA, 2011: 352-366. [145]MURMAN S M, AFTOSMIS M J, BERGER M J. Numerical simulation of rolling airframes using a multilevel Cartesian method[J]. Journal of Spacecraft and Rockets, 2004, 41(3): 426-435. [146]MURMAN S M. Reduced-frequency approach for calculating dynamic derivatives[J]. AIAA Journal, 2007, 45(6): 1161-1168. [147]李道春, 向锦武. 非线性二元机翼气动弹性近似解析研究[J]. 航空学报, 2007, 28(5): 1080-1084. LI D C, XIANG J W. Nonlinear aeroelastic analysis of airfoil using quasi-analytical approach[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(5): 1080-1084 (in Chinese). [148]杜鹏程, 宁方飞. 跨声风扇周向畸变流动的谐波平衡法计算[J]. 推进技术, 2012, 33(3): 391-397. DU P C, NING F F. Numerical simulation of transonic fan under circumferential inlet distortion using harmonic balance method[J]. Journal of Propulsion Technology, 2012, 33(3): 391-397 (in Chinese). [149]许建华, 宋文萍, 王龙. 谐波平衡法在旋翼前飞绕流数值模拟中的应用研究[J]. 空气动力学学报, 2013, 31(5): 546-552. XU J H, SONG W P, WANG L. Application of harmonic balance method in forward flight simulation for helicopter rotors[J]. Acta Aerodynamica Sinica, 2013, 31(5): 546-552 (in Chinese). [150]杨小权, 程苏堃, 杨爱明, 等. 基于时间谱方法的振荡翼型和机翼非定常黏性绕流数值模拟[J]. 航空学报, 2013, 34(4): 787-797. YANG X Q, CHENG S K, YANG A M, et al. Time spectral method for numerical simulation of unsteady viscous flow over oscillating airfoil and wing[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(4): 787-797 (in Chinese). [151]谢立军, 杨云军, 刘周, 等. 基于时间谱方法的飞行器动导数高效计算技术[J]. 航空学报, 2013, 34(6): 2016-2026. XIE L J, YANG Y J, LIU Z, et al. A high efficient method for computing dynamic derivatives of aircraft based on time spectral method[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(6): 2016-2026 (in Chinese). [152]陈琦, 陈坚强, 谢昱飞, 等. 谐波平衡法在非定常流场中的应用[J]. 航空学报, 2014, 35(3): 736-743. CHEN Q, CHEN J Q, XIE Y F, et al. Application of harmonic balance method to unsteady flow field[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(3): 736-743 (in Chinese). [153]陈琦, 陈坚强, 袁先旭, 等. 谐波平衡法在动导数快速预测中的应用研究[J]. 力学学报, 2014, 46(2): 183-190. CHEN Q, CHEN J Q, YUAN X X, et al. Application of a harmonic balance method in rapid predictions of dynamic stability derivatives[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(2): 183-190 (in Chinese). [154]RONCH A D. On the calculation of dynamic derivatives using computational fluid dynamics[D]. Liverpool: University of Liverpool, 2012: 139. [155]RONCH A D, VALLESPIN D, GHOREYSHI M, et al. Evaluation of dynamic derivatives using computational fluid dynamics[J]. AIAA Journal, 2012, 50(2): 470-484. [156]THOMPSON J R, FRINK N T, MURPHY P C. Guidelines for computing longitudinal dynamic stability characteristics of a subsonic transport: AIAA-2010-4819[R]. Reston: AIAA, 2010. [157]BADCOCK K, RICHARDS B, WOODGATE M. Elements of computational fluid dynamics on block structured grids using implicit solvers[J]. Progress in Aerospace Sciences, 2000, 36(5): 351-392. [158]BONFIGLIOLI A, CAMPOBASSO M, CARPENTIERI B. Parallel unstructured three-dimensional turbulent flow analyses using efficiently preconditioned Newton-Krylov solver: AIAA-2009-4137[R]. Reston: AIAA, 2009. [159]WOODGATE M A, BADCOCK K J. Implicit harmonic balance solver for transonic flow with forced motions[J]. AIAA Journal, 2009, 47(4): 893-901. 刘绪男, 博士研究生。主要研究方向: 高超声速空气动力学。 Tel.: 0731-84574792 E-mail: liuxuqd@126.com 刘伟男, 博士, 教授。主要研究方向: 计算流体力学研究与应用。 Tel.: 0731-84573137 E-mail: fishfather6525@sina.com 柴振霞女, 博士研究生。主要研究方向: 频域计算方法在非定常流动中的应用。 Tel.: 0731-84574792 E-mail: chaizhenxia@sina.cn 杨小亮男, 博士, 讲师。主要研究方向: 计算流体力学研究与应用。 Tel.: 0731-84574792 E-mail: yangxl_nudt@sina.com Research progress of numerical method of dynamic stabilityderivatives of aircraft LIU Xu, LIU Wei*, CHAI Zhenxia, YANG Xiaoliang College of Areospace Science and Engineering, National University of Defense Technology, Changsha410073, China Dynamic stability derivatives (for short, dynamic derivatives) are key aerodynamic parameters for designing the control system, investigating the dynamic instability boundary and studying the dynamic stability criteria of aircraft. After a brief summary of flight stability, the research progress made in the numerical simulation of aircraft dynamic stability parameters is described. The main dynamic derivative calculation methods applied over the past few years are reviewed with respect to the theoretical method, engineering approximation and computational fluid dynamics (CFD) simulation. The merits of these dynamic derivative prediction methods are identified, and problems with numerical simulation of dynamic derivatives in terms of theoretical basis, unsteady aerodynamic modeling, the precision and efficiency of the prediction methods are pointed out. A mature, reliable prediction of dynamic stability characteristic enables us to evaluate and select different air design plans so as to minimize the aircraft design cost and mitigate risk exposure. Finally, the development trend of numerical simulation of dynamic derivatives is prospected. numerical methods; computational fluid dynamics; stability; time domain analysis; dynamic derivatives 2016-01-11; Revised: 2016-02-17; Accepted: 2016-03-23; Published online: 2016-03-2915:29 s: National Natural Science Foundation of China (11172325, 11502292); NUDT Advanced Project (ZDYYJCYJ20140101) . Tel.: 0731-84573137E-mail: fishfather6525@sina.com 2016-01-11; 退修日期: 2016-02-17; 录用日期: 2016-03-23; 时间: 2016-03-2915:29 www.cnki.net/kcms/detail/11.1929.V.20160329.1529.008.html 国家自然科学基金 (11172325,11502292); 国防科学技术大学预研项目 (ZDYYJCYJ20140101) .Tel.: 0731-84573137E-mail: fishfather6525@sina.com 10.7527/S1000-6893.2016.0098 V211.3 A 1000-6893(2016)08-2348-22 引用格式: 刘绪, 刘伟, 柴振霞, 等. 飞行器动态稳定性参数计算方法研究进展[J]. 航空学报, 2016, 37(8): 2348-2369. LIU X, LIU W, CHAI Z X, et al. Research progress of numerical method of dynamic stability derivatives of aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2348-2369. http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn URL: www.cnki.net/kcms/detail/11.1929.V.20160329.1529.008.html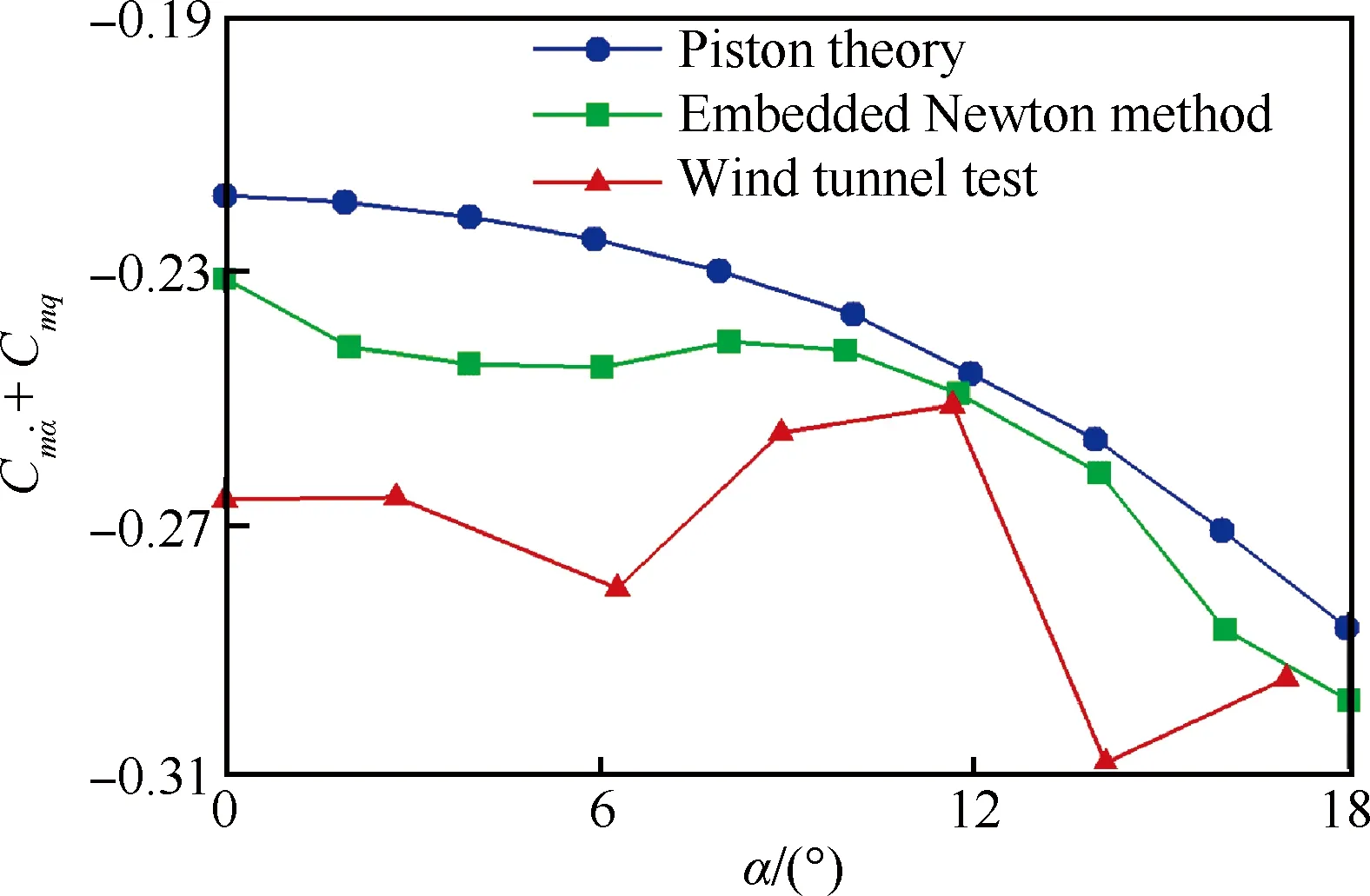
4 动导数时域计算方法


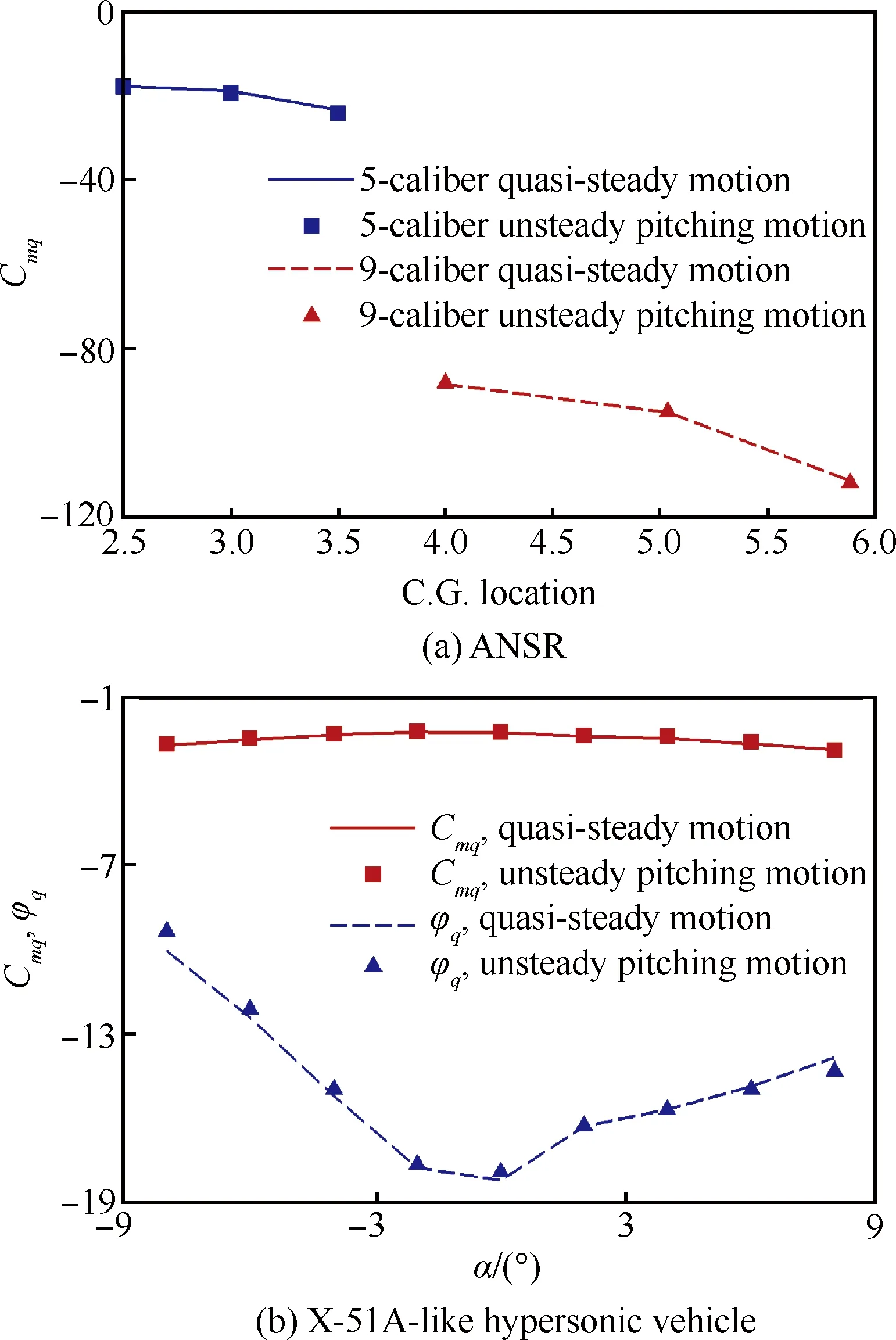

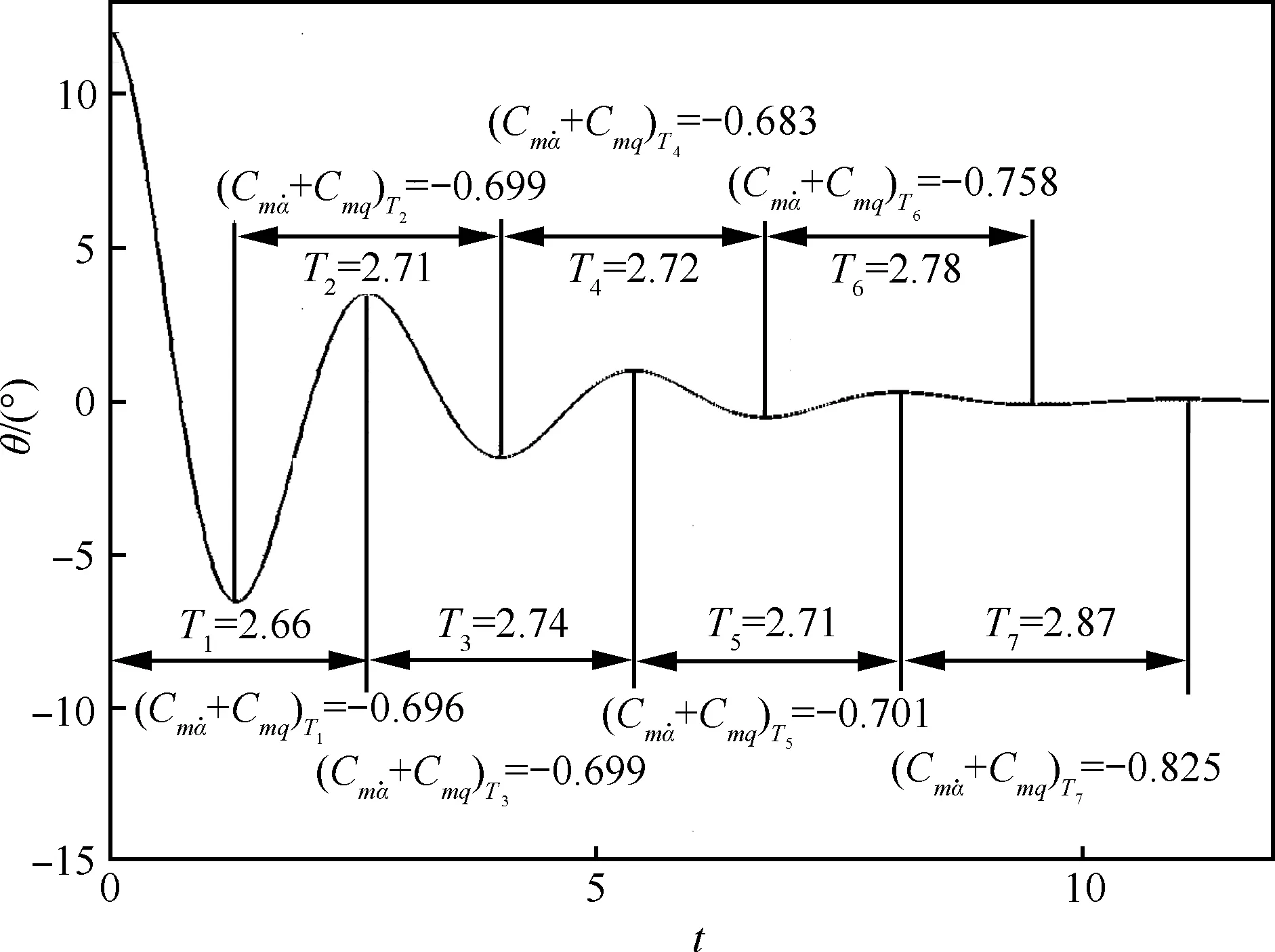
5 动导数频域计算方法




6 结 论
