虚谱法无反射速度-应力方程地震数值模拟

杜增利, 李春红, 傅雨濛, 李永章

(1.西南石油大学 地球科学与技术学院，成都 610500；2.中国石油大庆钻探工程公司 物探一公司，黑龙江 大庆 163357； 3.长安大学 建筑学院，西安 710018)



虚谱法无反射速度-应力方程地震数值模拟

杜增利1, 李春红2, 傅雨濛3, 李永章2

(1.西南石油大学 地球科学与技术学院，成都 610500；2.中国石油大庆钻探工程公司 物探一公司，黑龙江 大庆 163357； 3.长安大学 建筑学院，西安 710018)

基于单程波波场延拓算子的零偏移距地震数值模拟方法难以适应复杂地质条件下地震波速度的空间剧烈变化，且其最大成像角度有不同程度的限制。本文依据地震反射的形成机理，重置模型空间的密度分布，使得模型空间内纵波阻抗为常量以压制层间多次波；采用虚谱法可得到高精度的地震波场空间导数，因此可有效抑制空间数值频散，同时提高了数值模拟的垂向分辨率。数值模拟结果表明，得到的零偏移距地震记录绕射波场完整，偏移归位效果优于频率-波数域或频率-空间域的单程波模拟结果。无反射一阶应力-速度方程零偏移距数值模拟可有效压制多次反射波，在较大网格间距时，虚谱法仍可有效抑制数值频散。

虚谱法；有限差分；数值模拟；无反射；零偏移距

地震波场的复杂性使得复杂构造区地震、地质解释异常困难。随着计算机技术的迅猛发展，虽然方位各向异性的黏弹性等炮域地震数值模拟技术日趋成熟，但零偏移距地震数值模拟仍是验证解释方案正确性的有效手段之一[1-3]。目前，零偏移距地震记录数值模拟多采用频率-波数域或频率-空间域的单程波波场延拓算子。

当介质速度在整个模型空间为常数时，相移法(phase shift, 简称PS)能得到方程的精确解[4]，且算法无条件稳定、背景噪声低。Gazdag解决了速度的纵向变化问题，但仍不能适应地层速度的横向变化[5]；为了能同时解决速度横向变化和大倾角问题，在相移法基础上，Stoffa等提出了裂步傅里叶法(split step Fourier，简称SSF)，在频率-空间域增加了误差校正项，使之能处理横向速度变化较小的情况[6]。为使裂步傅里叶法能适应更强的速度横向变化，Kessinger使用多个参考速度，通过地震波场的Sinc插值得到任意速度的近似波场；但增加了计算量，导致计算效率降低[7]。为补偿舍弃速度摄动所引起的高阶误差，在裂步傅里叶法的基础上，Ristow 等增加了有限差分补偿项，即傅里叶有限差分法(finite Fourier difference，简称FFD)[8]。刘文革等进一步分析了傅里叶有限差分各阶近似的精度问题[9]。

尽管诸多学者对单程波波场延拓算子进行了各种近似处理，使之能够处理速度的横向变化，但对最大成像角度都有一定限制。而双程波波动方程既能处理速度的横向突变，又无地层倾角限制，但在零偏移距地震波场模拟中会产生多次反射。为压制层间多次波，Baysal等构建了无反射双程声波方程[10]；单延明等利用无反射双程声波方程制作了自激自收时间剖面[11]。

有限差分法采用离散化的差分方程来逼近波动方程，但受空间和时间采样密度的限制，该方法不可避免地会产生数值频散，为避免或减少此效应，网格半径一般都取很小并采用高阶差分。地震波场空间导数的计算方法主要有高阶有限差分法和虚谱法2种[12-14]。采用高阶有限差分法得到的地震波场空间导数在边界附近会出现振荡；而虚谱法是通过傅里叶变换求取地震波场的空间导数，无需模型空间边界外地震波场的参与。应用傅里叶变换求取空间导数时，由于傅里叶变换的周期性，非光滑函数的相位谱在奈奎斯特频率处的突变造成时、空域信号的周期性震荡，而在半网格点求导可有效克服Gibbs效应[12,16]。本文应用非均匀各向同性声学介质中的一阶压力-速度方程，采用虚谱法计算地震波场的空间导数实现零偏移距地震波场模拟。

1 声波方程

1.1 声波方程有限差分解

非均匀各向同性声学介质中的一阶应力-速度方程为[15-17]

(1)

其中:地震波场向量;P=(p,ux,uy,uz)T且p为应力;ux,uy,uz分别为x,y,z方向的速度分量; A1,A2,A3为模量矩阵，且有

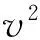
相应的差分解为[14]

(2)

其中：n表示当前时刻；n-表示前一时刻；Δt为时间采样率；f={fx,fy,fz}T为外力向量；L表示求导运算；i,j,k为空间坐标。

1.2 无反射条件

采用双程波动方程进行波场模拟时，地震波在通过介质分界面时既有透射也有反射，而在零偏移距地震记录正演过程中不希望有多次波出现，即希望地震波在通过介质分界面时只有透射而无反射。

众所周知，地震波在介质分界面上产生反射的前提条件是声阻抗存在差异，因此，通过人为设定介质密度使模型空间内声阻抗为常量就可以有效压制层间反射，即

ρi,j,k=v0/vPi,j,k

(3)

其中：v0为任意给定的速度常量。为了使得到的介质密度符合地质规律，v0一般取模型空间中的最大速度。

1.3 初始条件

根据爆炸反射面成像原理，在整个模型空间内的所有网格节点上均放置震源，震源强度为该点的反射系数，并在t=0时刻同时引爆。采用零相位Ricker子波作为震源，其函数为

w(t)={1-2[πf(t-t0)]2}e[πf(t-t0)]2

(4)

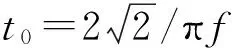
1.4 虚谱法空间差分计算

利用傅里叶变换计算半网格点处(交错网格)地震波场向量的空间一阶导数公式见文献[12]。

虚谱法与高阶(16阶)差分法在常速介质中的脉冲响应对比如图1所示，其中声波速度设为3 km/s，x和z方向的网格边长均为10 m。结果表明，采用16阶差分计算地震波场的空间导数，在Ricker子波主频为40 Hz时在地震波场中数值频散较明显，子波主频为35 Hz时地震波场中无数值频散发生；而采用虚谱法计算地震波场的空间导数，在Ricker子波主频为55 Hz时数值频散才较为明显，地震波场不产生数值频散的子波最高主频为50 Hz。由此可以说明，由于虚谱法可以得到高精度的地震波场空间导数，数值模拟时可以采用较高主频的地震子波(本例可提高15 Hz)，因而可以得到更高垂向分辨率的模拟结果。

1.5 边界条件

采用Collino等给出的一阶应力-速度弹性波数值模拟的完美匹配层吸收边界条件(PML)[18]，其基本思想就是人为地将地震波场分解为垂直和平行于传播方向的2组波，并使其中的沿界面法向方向传播的地震波场在衰减带内快速衰减，以达到减少边界反射的目的[17-18]。

2 数值模拟实例

2.1 SEG/EAGE模型

SEG/EAGE模型(图2-A)主要针对大倾角地层和高速膏岩层边界及其下伏地层成像问题而设计，其参数为：长51 560 ft (1 ft=30.48 cm)，深12 000 ft，Δx=Δz=40 ft，x方向网格数1 290，z方向网格数301。

图1 常速介质中的脉冲响应对比Fig.1 Comparison of snap shots in constant velocity medium(A)子波主频为35 Hz的16阶差分法结果; (B)子波主频为40 Hz的16阶差分法结果; (C)子波主频为50 Hz的虚谱法结果; (D)子波主频为55 Hz的虚谱法结果

单程波波动方程零偏移距地震数值模拟采用相移加插值算法，为保证插值的准确度，参考速度最多取7个，其合成记录只有一次反射波和绕射波(图2-B)。由于无最大倾角限制，常规的双程波一阶应力-速度方程零偏移距数值模拟结果中绕射波场更加丰富(图2-C中蓝色箭头所示)；但多次反射波较强(图2-C中红色箭头所示)，多种波场的叠加效应导致中深层背景噪声较强(图2-C中红色矩形框所示)。与常规的双程波方法结果相比，无反射条件的双程波零偏移距数值模拟结果中多次反射得到了较好的压制(图2-D中红色箭头所示)，进而减弱了中深层的背景噪声(图2-D中红色矩形框所示)。

为验证地震数值模拟结果的准确性，采用裂步傅里叶加插值法进行深度偏移处理。结果表明，受单程波波场延拓算子最大成像倾角的限制，相移加插值法单程波正演、裂步傅里叶加插值法深度偏移结果在大倾角盐丘边界处成像较差(图3-A，红色箭头所示)，且有偏移过量造成偏移划弧现象(图3-A，蓝色箭头、蓝色方框所示)。由于常规的双程波正演结果中多次波发育，裂步傅里叶加插值法深度偏移后多次波同样成像(图3-B，蓝色箭头所示)，在剖面上造成地质假象，影响地质人员正确认识地下地质特征；同时，多次波和绕射波场叠加导致深度偏移不能准确归位，中深层信噪比较低(图3-B，蓝色方框所示)。由于无倾角限制，无反射双程波正演、裂步傅里叶加插值法深度偏移后，图3-C中红色箭头所示位置的大倾角盐丘边界成像质量明显提高，且无偏移过量的划弧现象(图3-C，蓝色箭头、蓝色方框所示)。

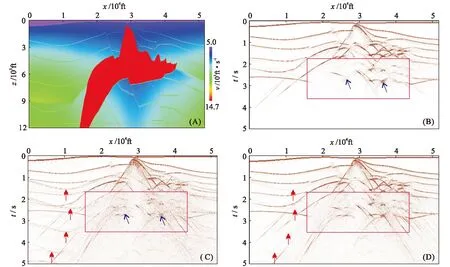
图2 SEG/EAGE模型及零偏移距正演结果对比Fig.2 SEG/EAGE velocity model and comparison of zero offset simulation results(A)SEG/EAGE速度模型; (B)单程波数值模拟结果; (C)常规双程波动方程数值模拟结果; (D)无反射双程波动方程数值模拟结果。1 ft=30.48 cm

图3 SEG/EAGE模型叠后深度偏移结果对比Fig.3 Comparison of post-stack depth migration in SEG/EAGE model(A)相移加插值法单程波正演、裂步傅里叶加插值法深度偏移结果; (B)常规双程波正演、裂步傅里叶加插值法深度偏移结果; (C)无反射双程波正演、裂步傅里叶加插值法深度偏移结果。1 ft=30.48 cm

2.2 Sigsbee模型

采用Sigsbee模型(图4-A)测试数值模拟方法对地质界面剧烈变化和高速膏岩层边界的适应性，模型参数为：长16 000 ft (1 ft=30.48 cm)，深6 000 ft，Δx=Δz=10 ft，x方向网格数1 600，z方向网格数600。

数值模拟结果表明，常规的双程波一阶应力-速度方程零偏移距数值模拟结果(图4-C)较单程波正演结果(图4-B)在深层绕射波更完整(图4-C，蓝色箭头所示)，但多次波发育(图4-C，蓝色方框所示)；无反射条件的双程波零偏移距数值模拟结果中多次反射得到了较好的压制(图4-D，蓝色方框所示)，中深层信噪比显著提高。采用裂步傅里叶加插值法进行的深度偏移处理结果表明，无反射双程波正演、裂步傅里叶加插值法深度偏移后陡倾角盐丘边界成像质量明显提高(图5，蓝色方框所示)。

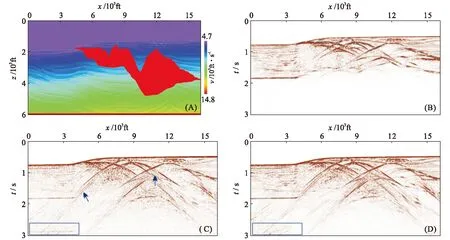
图4 Sigsbee速度模型及零偏移距正演结果对比Fig.4 Sigsbee velocity model and comparison of zero offset simulation results(A)速度模型; (B)单程波数值模拟结果; (C)常规双程波动方程数值模拟结果;(D)无反射双程波动方程数值模拟结果。1 ft=30.48 cm

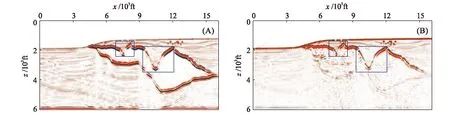
图5 Sigsbee模型叠后深度偏移结果对比Fig.5 Comparison of post-stack depth migration in Sigsbee model(A)相移加插值法单程波正演、裂步傅里叶加插值法深度偏移结果;(B)无反射双程波正演、裂步傅里叶加插值法深度偏移结果。1 ft=30.48 cm

3 结 论

a.使模型空间内声阻抗为常量进行全波一阶应力-速度方程零偏移距数值模拟可有效压制多次反射波，在较大网格间距时，虚谱法仍可有效抑制数值频散。

b. 无反射双程波一阶应力-速度方程零偏移距数值模拟可以适应速度的空间突变和陡倾角地层，是复杂构造区零偏移距地震波场模拟的有效手段。

[1] Claerbout J F. Imaging the Earth’s Interior [M]. London: Black Well Scientific Publications Inc, 1985.

[2] Sherif R E, Geldart L P. Exploration Seismology [M]. New York: Cambridge University Press, 1995.

[3] Aki K, Richards P. Quantitative Seismology [M]. San Francisco: W H Freeman Co, 1980.

[4] Stolt R H. Migration by Fourier transform[J]. Geophysics, 1978, 43(1): 23-48.

[5] Gazdag J. Wave equation migration with the phase-shift method[J]. Geophysics, 1978, 43(7): 1342-1351.

[6] Stoffa P L, Fokkema J T, de Luna Freire R M,etal. Split-step Fourier migration[J]. Geophysics, 1990, 55(4): 410-421.

[7] Kessinger W. Extended split-step Fourier migration[C]//1992 SEG Annual Meeting. Society of Exploration Geophysicists, 1992: 917-920.

[8] Ristow D, Rühl T. Fourier finite-difference migration[J]. Geophysics, 1994, 59(12): 1882-1893.

[9] 刘文革，贺振华，黄德济，等. 高精度傅立叶有限差分法模型正演[J]. 石油地球物理勘探，2007，42(6)：629-633.

Liu W G, He Z H, Huang D J,etal. Forward modeling by Fourier finite difference approach[J]. Oil Geophysical Prospecting, 2007, 42(6): 629-633. (In Chinese)

[10] Baysal E, Kosloff D D, Sherwood J W C. A two-way nonreflecting wave equation[J]. Geophysics, 1984, 49(2): 132-141.

[11] 单延明，吴清岭，于承业，等. 复杂地质构造波动方程数值模拟[J].物探化探计算技术，2002，24(1)：22-26.

Shan Y M, Wu Q L, Yu C Y,etal. Wave equation modeling for complex media[J]. Techniques for Geophysical and Geochemical Exploration, 2002, 24(1): 22-26. (In Chinese)

[12] Corrêa G J P, Spiegelman M, Carbotte S,etal. Centered and staggered Fourier derivatives and Hilbert transforms[J]. Geophysics, 2002, 67(5): 1558-1563.

[13] Chung E T, Lam C Y, Qian J. A staggered discontinuous Galerkin method for the simulation of seismic waves with surface topography[J]. Geophysics, 2015, 80(4): T119-T135.

[14] Amundsen L, Robertsson J O A. Wave equation processing using finite-difference propagators, Part 1: Wavefield dissection and imaging of marine multicomponent seismic data[J]. Geophysics, 2014, 79(6): T287-T300.

[15] 杜增利，徐峰，高宏亮.虚谱法交错网格地震数值模拟[J].石油物探，2010，49(5)：430-437.

Du Z L, Xu F, Gao H L. Pseudo spectral seismic wavefield simulation with staggered grid [J]. Geophysical Prospecting for Petroleum, 2010, 49(5): 430-437. (In Chinese)

[16] 牟永光，裴正林.三维复杂介质地震数值模拟[M].北京：石油工业出版社，2005.

Mu Y G, Pei Z L. Seismic Numerical Modeling for 3-D Complex Media[M]. Beijing: Petroleum Industry Press, 2005. (In Chinese)

[17] 杜增利，李亚林，尹成，等. 虚谱法速度应力方程地震数值模拟[J].石油地球物理勘探，2009，44(5)：637-641.

Du Z L, Li Y L, Yin C,etal. Pseudo spectral seismic simulation with one order stress-velocity equation[J]. Oil Geophysical Prospecting, 2007, 42(6): 637-641. (In Chinese)

[18] Collino F, Tsogka C. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media[J]. Geophysics, 2001, 66(1): 294-307.

Non-reflection numerical simulation of zero offset seismic wavefield with velocity-stress equation based on pseudo spectral method

DU Zeng-li1, LI Chun-hong2, FU Yu-meng3, LI Yong-zhang2

1.SchoolofGeosciencesandTechnology,SouthwestPetroleumUniversity,Chengdu610500,China; 2.No.1GeophysicalExplorationCompany,DaqingDrilling&ExplorationEngineeringCorporation,CNPC,Daqing163357,China; 3.SchoolofArchitecture,Chang’anUniversity,Xi’an710018,China

Since the wavenumber inzaxis may not be calculated directly and correctly when P-wave velocity varies dramatically inx-yplane, zero offset seismic numerical simulation based on one-way wave equation is not suitable in the complex geological areas, and the maximum imaging angle of wavefield extrapolation operators based on one-way wave equation is limited. According to the formation mechanism of seismic reflection, the density distribution is calculated manually to make the P-wave impedance is constant in the model space, thus the multiple reflections generated from impedance interfaces are decreased. The precision of spatial derivative of the seismic wave field calculated by pseudo spectral method is higher than that of finite difference, therefore, the numerical dispersion is suppressed effectively, and the vertical resolution is enhanced. Numerical simulation results show that the diffraction wave field in zero offset seismic data is abundant, and the effect of seismic migration is better than that of frequency wave number domain or frequency space domain based on one-way wave equation.

pseudo spectral method; finite difference; numerical simulation; non-reflection; zero offset seismic data

10.3969/j.issn.1671-9727.2016.05.12

1671-9727(2016)05-0617-06

2015-10-14。

国家科技重大专项(2011ZX05049)。

杜增利(1969-)，男，博士，副研究员，研究方向：地球物理勘探, E-mail:duzl0896@126.com。

P631.4

A