地震作用下弃土场高边坡稳定性有限元分析
2016-11-12杨俊毅
杨俊毅,罗 磊
(1.云南省公路工程监理咨询公司, 云南 昆明 650000; 2.金土石科技(北京)有限公司, 北京 100000)
地震作用下弃土场高边坡稳定性有限元分析
杨俊毅1,罗 磊2
(1.云南省公路工程监理咨询公司, 云南 昆明 650000; 2.金土石科技(北京)有限公司, 北京 100000)
为了探讨地震扰动下弃土场边坡稳定性,以沾会高速公路Q-6弃土场高边坡为研究对象,利用RS2(Phase2)有限元数值分析软件并结合Newmark积分法,建立边坡分析模型。根据地震时程曲线,将模型分为7个过程以模拟、分析不同时段边坡应变、位移及塑性区的变化规律。分析结果表明:地震发生后的前10 s对边坡影响较大,地震水平力更易激发坡脚的破坏;坡面中上部的水平位移最大,且其加速度放大现象很明显。
弃土场;安全系数;动载;位移;RS2(Phase2)软件
目前,随着计算机及数值模拟软件的发展,数值分析已经能较为真实地模拟边坡在地震作用过程中的动力特性和破坏机制,是边坡地震反应分析的主流方法[1]。目前常用于边坡地震稳定性分析的数值方法主要有有限单元法[2-3]和有限差分法[4-5]。
云南省是我国地震高发地带,据统计,近几十年云南省共发生5.9级以上的强地震8次。沾会高速公路位于云南省曲靖市鲜水河—滇东地震带和右江地震带区域,其中鲜水河—滇东地震带是强震发生带,其地震活动不仅强度大,而且频度高。
由于沾会高速公路Q-6弃土场范围内没有地震时程记录,故本文取相邻场地田坝特大桥地震勘察合成的基岩地震动时程作为计算参数,并结合RS2(Phase2)有限元边坡稳定性性分析方法,对Q-6弃土场高边坡的稳定性进行分析和评价。
1 动力响应时程分析
时程分析法[6]是根据材料及构件的弹性(或非弹性)性能对结构动力方程做积分求解的方法。该方法既能考虑地震的振幅、频谱和持时3个要素的影响,又能考虑地震环境和场地条件的影响,还能对结构进行非线性分析,而且还可以计算能量损耗和损伤等,并由此获得更多的有用信息,因此,可以说时程分析法是一个真正的动力分析方法。目前结构地震反应分析中较常用的时程分析法有线性加速度法、Wilson法和Newmark法等。本文主要采用Newmark法进行地震分析,阻尼模型选择瑞利阻尼。Newmark解析方程如下:
vi+1=vi+[(1-γ)Δt]ai+(γΔt)ai+1
(1)
ui+1=ui+(Δt)vi+[(1/2-β)(Δt)2]ai+[β(Δt)2]ai+1
(2)
式中:u为位移;v为速度;a为加速度;Δt为时间增量;β、γ均为加速度变化系数。Newmark积分中β、γ的标准取值如表1所示。

表1 Newmark积分中β、γ标准值
2 工程实例
沾会高速公路Q-6弃土场位于云南省曲靖市田坝乡,弃土约为71万m3,占地约5.67 hm2。据地面调查及钻探揭露,场地内地层主要为新生界第4系全新坡洪积层(Q4dl+pl)、坡残积层(Q4dl+el)、崩坡积层(Q4c+dl)、古生界二叠系下统栖霞+茅口组(Plq+m)及古生界寒武系(∈)。Q-6弃土场位于沾益“山”字型构造西翼与新华夏系构造复合地带白石岩-小河水大向斜西翼,构造线近东西向展布为主,有水堰塘断层和田坝断层发育。
该弃土场边坡高达60 m,且区域内地震活跃,故有必要对其边坡动力响应进行评价。
2.1 计算参数
由于Q-6弃土场没有实测地震加速度数据,本文选取相邻场地田坝特大桥实测50年超越概率
39%数据为对象合成地震加速度时程曲线,如图1所示,地震作用过程总历时约40 s。边坡有限元网格划分模型如图2所示。

图1 地震波时程曲线
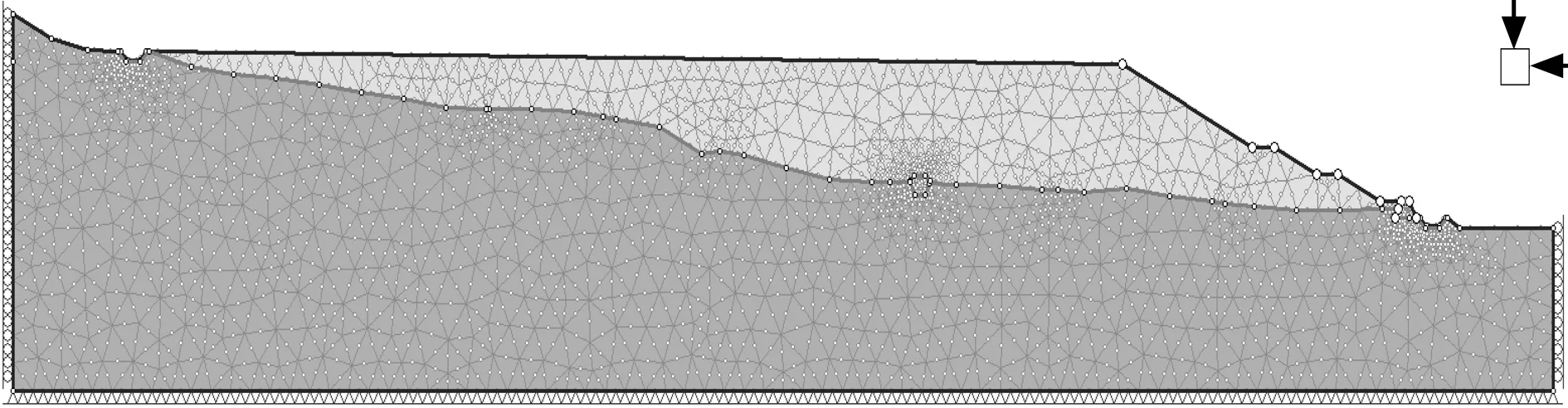
图2 有限元网格划分模型
定义模型左右两侧边界条件为Lysmer-Kuhlemeyer,运用Lysmer-Kuhlemeyer边界条件可以模拟无限土壤介质的边界行为。计算过程中,岩土数值模拟参数来采用试验数据及经验类比值,具体参数参如表2所示。单元的阻尼矩阵采用瑞利阻尼(Rayleigh Damping)[7-8],瑞利阻尼模型计算公式为:
[C]=a[M]+b[K]
(3)
式中:[C]为粘性阻尼矩阵;[M]为质量矩阵;[K]为刚度矩阵;a、b均为常数。
根据公式(3),取频率1为4 Hz,阻尼系数为0.2;取频率2为8 Hz,阻尼系数为0.2。地震荷载分为6步加载,第1~6步加载时间分别为1、3、5、10、20和40.94 s。

表2 岩土数值模拟参数
2.2 边坡动力响应分析
进行Q-6弃土场边坡动力时程分析时,根据地震加载方式,可对全部边坡的每个单元应力时程、位移时程、各节点加速度时程进行研究。选取坡顶节点查询Q-6弃土场的塑性区分布(选取有代表性的第1、4、6步加载计算结果)及水平位移分布,塑性区分布如图3所示,水平位移分布如图4所示。
由图3可以看出,当地震发生10 s时,整个边坡已经全部破坏;坡脚塑性区范围最广。可见后期地震对边坡的影响较小,地震水平力更易激发坡脚的破坏,这主要与边坡的坡形和结构有关。

图3 Q-6弃土场塑性区分布

图4 Q-6弃土场水平位移分布
由图4可以看出,最大水平位移出现在动力第2步(3 s)边坡中上部,最大位移达47.2 cm;地震发生后的前5 s,水平位移变化显著,后期随着地震波的衰减,对边坡的影响逐渐降低。
3 结论
弃土场高边坡在地震荷载作用下的动力响应是工程界较为关心的问题,但由于实际施工过程中土石比及压实度等参数控制比较困难,因此弃土场高边坡的稳定性分析较为复杂,而运用数值模拟方法分析结果可以很好地对工程进行预判。本文应用动力响应时程分析原理,采用RS2(Phase2)有限元数值模拟方法,以沾会高速公路Q-6弃土场为研究对象,对该弃土场高边坡在地震荷载下的扰动作用进行了研究,并得到如下结论:
1) 在地震作用下,地震发生10 s时,整个边坡已经全部破坏,后期地震对边坡的影响较小,可见地震水平力更易激发坡脚的破坏。
2) 最大位移出现在动力第2步边坡中上部,且坡面顶部加速度放大现象很明显。
3) 时程分析法能够较为真实地反映动力响应结果及地震对边坡的扰动作用。
[1] 刘红帅,薄景山,刘德东.岩土边坡地震稳定性分析研究评述[J].地震工程与工程振动,2005,25(1):164-171.
[2] 薄景山,徐国栋,景立平.土边坡地震反应及其动力稳定性分析[J].地震工程与工程振动,2001,21(2):116-120.
[3] 陈玲玲,陈敏中,钱胜国.岩质陡高边坡地震动力稳定分析[J].长江科学院院报,2004,21(1):33-35.
[4] 刘春玲,祁生文,童立强,等.利用FLAC3D 分析某边坡地震稳定性[J].石力学与工程学报,2004,23(16):2730-2733.
[5] 祁生文.边坡动力响应分析及应用研究[D].北京:中国科学院地质与地球物理研究所,2002.
[6] 顾淦臣.土石坝地震工程[M].南京:河海大学出版社,1987.
[7] 黄宗明,白绍良.结构地震反应时程分析中的阻尼问题评述[J].地震工程与工程振动,1996,2(16):95-105.
[8] LEGER P,DUSSULT S. Seismic-energy dissipation in MDOF structures[J].Journal of structure Engineering,ASCE,1992,118(5):113-124.
Finite Element Analysis to Spoil Ground High Slope Stability under Earthquake Impact
YANG Junyi1, LUO Lei2
This paper explores stability of spoil ground slope under earthquake impact. It utilizes Q-6 spoil ground high slope on Zhanyi-Huize Highway as study object, using RS2 (Phase2) finite element numeric analysis software integrated with Newmark integration method, to set up the analytical model of the slope. According to time travel curve of earthquake, we divided the model into 7 processes to simulate and analyze slope strain, displacement and variation rules of the plastic zone under different time interval. Results show that the first 10 s of earthquake has relatively heavy influence to side slope, the horizontal force of earthquake may easily cause damage to slope foundation. The maximum horizontal displacement occurs at the middle and upper part of the slope and the magnification of acceleration is quite obvious.
spoil ground; safety coefficient; dynamic load; displacement; RS2 (Phase2) software
10.13607/j.cnki.gljt.2016.05.006
2016-06-29
杨俊毅(1977-),男,云南省昆明市人,本科,高工。
1009-6477(2016)05-0021-03
U416.1+4
A
