基于支持向量机的服装号型推荐模型建立

毛连忠，郝矿荣，丁永生，

基于支持向量机的服装号型推荐模型建立

毛连忠，郝矿荣，丁永生，

消费者网上购衣需要一种方便有效的服装号型推荐方法，为此提出了一种基于支持向量机的服装号型推荐模型，以解决消费者在选购服装尺寸上遇到的困难。首先根据人体的数据信息与服装对应型号的数据信息，定义合身度评价函数来得到不同体型的人适合的号型，从而构建一个号型归档数据库。实验结果表明采用基于支持向量机的分类方法对比采用BP神经网络模型的方法进行模型推荐的准确率更高，由此证明选择支持向量机模型更适合服装号型的推荐。

服装号型；支持向量机；合身度；号型归档；神经网络

0　引言

近年来，随着互联网电子商务的普及和网络购物的快速发展，作为网络购物中受众面最为广泛的服装板块，其消费需求也经历着成倍数的增长。而消费者在选中了自己喜欢的款式之后，在网上按照自己的尺寸选购衣服，之后却发现不合身。只能选择退换或者将就着穿，对网购信任度受到影响。那么帮助消费者选择令他们满意的服装是一个需要解决的问题，我们建议找出一种服装号型推荐的方法来解决这个难题。

目前，在国内外对于服装号型的推荐已经有了不少研究，于晓坤等人在文献[1]中提出了人体的胸型、腰型和臀型理论，并且分析了人体体型与服装号型的匹配原则及方法，为服装匹配等应用程序的编写提供了一定的理论基础，但是该方法只考虑了胸型，腰型以及臀型的数值，对于肩宽，臂长等同样影响服装匹配的关键特征没有做到充分的考虑。而近几年来，神经网络算法在解决服装合体性、服装号型推荐方面取得了一定的成果。目前有部分研究将神经网络算法运用于服装号型的推荐，郑爱花通过一个改进BP算法，选择Levenberg-Marquardt优化法的BP神经网络作为号型推荐模型，结果显示该网络适合应用于服装号型推荐。但是在部分特殊体型的号型推荐上，效果还不尽理想。东苗等人将专家系统、模糊神经网络的计算优势与服装号型相结合实现了面向个体尺寸的服装号型推荐，提出了基于模糊神经网络的服装号型推荐专家系统[2]。但是由于模糊逻辑系统缺乏记忆无法从错误中学习，而且没有记忆能力，所以该系统不具备优化系统效率的能力。

考虑到网上购物需要结合人体多部位数据进行服装的推荐，本文在构建的服装号型匹配库的基础上首次把 SVM算法应用到服装号型的推荐方法[3]。首先，基于测量获取的多组人体特征部位尺寸数据以及现有服装号型的尺寸数据，针对同一类型衣服的不同号型建立一个合身度评价的函数方程，以此构建一个服装号型匹配数据库。然后采用 SVM多分类[4]的方法对该数据库的匹配准确率进行验证，进而与BP神经网络模型做比较，根据比较结果最后选择采用SVM模型的预测函数对其进行号型推荐。

1　服装号型匹配数据库的建立

1.1人体特征部位尺寸数据的获取

本文研究的对象主要是上海地区18-24岁的女子。本文选取松江大学城7所高校的学生作为采样目标。问卷的内容是收集她们的身高h，颈围n，胸围b，肩宽s，腰围w五个部位的尺寸数据。尺寸数据获取的方法是采用接触式测量的方法获取。

1.2服装各个号型尺寸数据的获取

由于我国服装号型以个体胸围或腰围及身高为依据，服装的号（身高）每5厘米分一档，胸围每4厘米分一档，以5·4系列女长袖衬衫规格系列为例，服装的号从155-175cm，5厘米分为一档，共5个；胸围从80-104cm，4厘米分一档，共7个。

考虑到调查的对象穿着的尺码的号主要集中分布在155-170之间，胸围主要分布在80-92之间，以网上购买某款女衬衫为例，它的号型分布在S、M、L、XL这4种款式，所以本文选用该款女衬衫作为服装的推荐款式。该四种号型的尺寸数据如表1所示。

表1　5·4系列女长袖衬衫号型尺寸数据Tab.1 Size data of 5·4 series of blouse

根据提供的号型尺寸数据表，我们可以获取每种号型对应的身高H，领围N，胸围B，肩宽S和腰围W的尺寸数据。

1.3合身度评价函数方程建立

1.3.1特征部位差值百分比的确定

根据1.1节和1.2节获得的人体特征部位尺寸数据以及服装对应的各个部位的尺寸数据，分别计算它们之间对应的差值百分比如公式（1）～（5）：

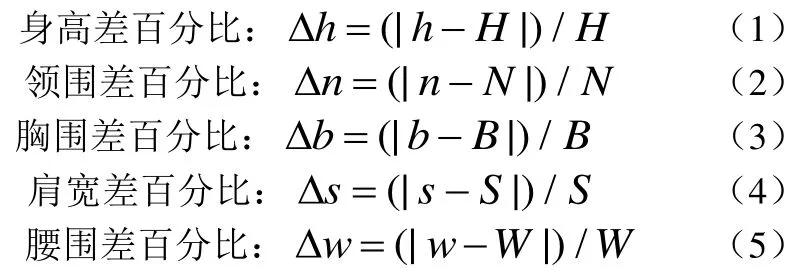
（其中h，n，b，s，w分别表示人体的身高，颈围，胸围，肩宽和腰围。）

1.3.2舒适度重视因子的确定

舒适度重视因子是指人对身体各部位的服装舒适感的重视程度的标准化权重因子。对于人体而言，每个部位都有这样一个系数，该系数的数值介于0到1之间，且所有系数之和为1。为了确定舒适度因子的大小，我们采用专家打分法来确定。

本文的方案是：随机选取大学以及研究生的女性同学100位，其中包含了各个体型的人。然后设计问卷调查的题目，本文调查的内容是对颈部，胸部，肩部以及腰部的穿衣舒适度的重视程度如何。答案需要给出0～1之间的一个数值，且所有部位的舒适度相加总和为1。经过调查之后。分别统计各个身体部位的舒适度重视因子的平均值，最后得出颈部的舒适度重视因子n*=0.3，胸部的舒适度重视因子b*=0.4，肩部的舒适度重视因子s*=0.2，腰部的舒适度重视因子w*=0.1。

1.3.3合身度评价函数方程的建立

影响穿衣舒适性的因素称为服装放松量。服装放松量是服装相对人体放松的量值，它不仅直接影响着服装的舒适性，而且是确定服装空间造型的关键因素[5]。除此之外，人对身体各部位的服装舒适感的重视程度有所不同，因而这也影响到选择衣服的问题。所以综上所述本文将服装放松量以及舒适度重视因子作为判别因素来构建合身度评价函数方程。

将人体特征部位差值百分比以及舒适度重视因子两者结合起来对服装的合身度进行综合评价。

合身度评价⑥函数定义如公式（6）：n*、b*、s*、w*分别为颈部、胸部、肩部以及腰部的舒适度重视因子，Δh 、Δn 、Δb 、Δs 、Δw分别是公式（1）-（5）定义的各特征部位的差值百分比。n*+b*+s*+w*=1，f＜1。

由于各个部位均取的是差值，对应的服装f版型又属于修身型，所以差值之和越小表示越合身，即越小表示衣服越合身。

1.3.4号型确定方法

首先我们选择S号型。用公式（6）计算合身度函数值为fS，接下来按照相同的方法我们分别选择 M，L，XL分别计算出它们的合身度函数值fM，fL，fXL，再分别比较它们之间的大小，选取其中数值最小的数值对应的号型作为推荐的型号。

我们以第一个人为例：第一个人的身高为156cm，颈围35.7cm，胸围76.5cm，肩宽35.7cm，腰围68cm。S号型对应的身高为155cm，领围36cm，胸围80cm，肩宽37cm，腰围 72cm，根据该人选择的不同号型衣服，计算出对应的身高差百分比、领围差百分比、肩宽差百分比、胸围差百分比和腰围差百分比，最后计算对应的合身度函数值。结果如表2所示：

表2　样本1对应的各部位差值百分比

由表2可知：

2017年11月，美国霍尼韦尔国际公司(Honeywell International)宣布美国唯一铀转化厂即梅特罗波利斯(Metropolis)厂暂停运行。

fS＜fM＜fL＜fXL，所以给她推荐的号型为S。

依照此方法，依次对选取的剩下样本进行推荐，最后得到一个号型匹配数据库。该号型匹配数据库包含了各种体型的对象。由于数据量过大，只选取了其中10组样本作为参例。如表3所示：

表3　其中十组样本对应的人体特征部位尺寸和推荐号型

2　SVM进行服装号型推荐

消费者在网上选购衣服型号时，需要根据某种标准进行选择适合自己的型号，由于每种品牌都有各自的标准，包括身高、胸围、腰围、颈围和肩宽等尺寸的数据。对应这些数据消费者往往会根据自身的相应部位尺寸数值进行决策。而该问题便转换成了一个分类问题，即将人如何归类对应的衣服号型里面。但由于人体有很多部位指标数据，维度升高，同时调查问卷获取的数据少，传统的分类方法已经不再适用，而SVM方法正好可以解决这类问题。因此本文通过构造 SVM模型以帮助消费者对网上购衣做出适合的号型推荐。我们将身高、肩宽、胸围、腰围、和颈围作为自变量，将可供选择的号型作为因变量Y，构建SVM模型。

2.1归一化数据

样本数据中包含的先验信息会对优化后分类器的性能产生直接的影响。所以首先需要对样本数据进行预处理。预处理的目的是将数据可分性达到合理的水平，从而使得不同量纲、不同数量级的数据具有可比性。与此同时，归一化之后的数据矩阵可以提高模型数据运算的速度，有效地解决计算过程中出现的数值困难等问题。本文采用线性极差变换对样本数据进行预处理。

2.2训练样本和测试样本确定

经过数据预处理之后，将归一化之后的新矩阵作为SVM 模型的维度数据即输入数据。我们将可供选择的号型作为SVM模型的输出数据，由于本次分类总共有4类，分别为S，M，L，XL。我们将他们用标签的方法进行代替这些类别，即分别对应1，2，3，4这4个类别。

算法思想如下：

该算法是将训练样本中的每两类作为一个二类分类问题，如果有n类，则要训练n*(n-1)/2个分类器，用每个分类器来预测测试样本，得到 n*(n-1)/2个预测结果。根据结果对 n类进行投票，得到票数最多的即为测试样本所属类别。

为了更好地提取训练样本数据和测试样本数据，首先我们把数据库里的数据按照类别顺序依次排列。即：第1类数据：1～64。第2类数据：65～110。第3类数据：111～152。第4类数据：153～180。

我们将数据库里每类的数据分成两部分，一半作为训练集一半作为测试集。

（1）训练样本的选择：

首先选择训练样本集，我们选取第1类的1～32，第2类的65～87，第3类的111～131，第4类的153～180组数据作为训练样本。选取他们的序号作为行向量，选取他们的特征部位的数值作为列向量，构建一个90*6的矩阵作为训练样本。然后将他们对应的分类作为训练样本的标签，矩阵维数为90*1。

（2）测试样本的选择：

首先选择测试样本集，我们选取第1类的33～64，第2类的88～110，第3类的132～152，第4类的167～180组数据作为训练样本。选取他们的序号作为行向量，选取他们的特征部位的数值作为列向量，构建一个90*6的矩阵作为训练样本。然后将他们对应的分类作为训练样本的标签，矩阵维数为90*1。

（3）选取核函数

SVM 用于分类时，核函数的选择以及相应参数的确定十分关键[7]。然而，目前学术界对于核函数及参数的选择还没有形成统一模式，最常见的方法包括按照以往经验选取或者通过进行多次实验对比寻优、或者通过交叉检验寻找最优参数。因此本文首先选取不同的核函数分别进行实验，然后对实验结果进行比较，从而选择最优分类核函数。本文采用Libsvm3.20软件包进行实验，实验选取的数据为经过归一化预处理之后的训练样本数据和测试样本数据。在选择核函数的时候我们分别做四组实验，分别选用不同的核函数，在参数c选择为20，其他参数为默认值下进行实验如表4所示：

表4　不同核函数下的结果

通过表4的四组实验结果可以看出，线性函数，RBF函数以及Sigmoid函数分类的准确率较高，多项式函数准确率偏低，所以不宜选择。

另外，RBF核函数具有如下优点：RBF函数不仅能处理非线性的情况（线性核函数属于RBF核函数的特例），而且能比多项式核函数更简单快速地进行参数调整。综合考虑选择RBF核函数作为SVM模型的核函数。

（4）参数寻优

本文利用LIBSVM 工具包使用交叉检验的方法来寻求最优参数。本文通过easy.py 寻找 RBF 核函数的最优参数，easy.py 文件通过对 grid.py、svm-train、svm-predict 等模块的调用，实现从参数优选，到预测分类的目的。最终的最优参数为c=20，g=0.04。采用此参数准确率提高到了91.11%。

训练集分类结果如图1所示：

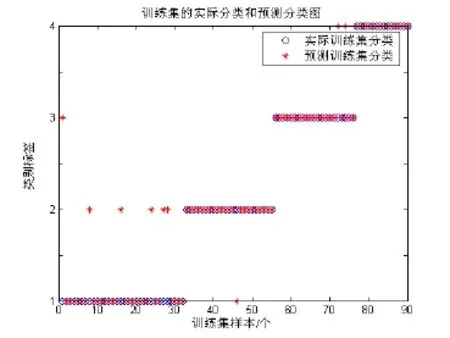
图1：　训练集预测结果图

训练集预测分类准确率为90%（81/90）。

测试集分类结果如图2所示。

图2：　测试集预测结果图

从图2我们可以看出第1类分类准确率为96.8%，第2类分类准确率为82.6%，第3类分类准确率为85.7%，第4类分类准确率为100%。

3　实验对比

目前有部分研究将BP神经网络算法运用于服装号型的推荐，所以本文将BP神经网络模型的分类结果与SVM模型的分类结果加以比较，探索更适合服装号型推荐的模型方法。

在BP神经网络模型中，我们运用交叉检验的方法得到目标误差为 0.00001，隐含层个数为 10，最大训练次数为10000次，训练显示间隔设为1。在MATLAB中调用训练函数trainlm函数，对测试样本进行分类预测。测试样本预测结果准确率如表5所示。

比较BP神经网络的预测样本的分类结果与SVM的分类结果，如表5所示：

表5　BP与SVM分类准确率对比结果

通过比较的分类结果我们发现SVM的分类准确率要高于BP神经网络的分类准确率。因此，从整体分类准确率的角度看，SVM模型要优于BP神经网络模型。并且SVM模型在每类分类准确率都好于BP神经网络。所以选择SVM进行服装号型推荐要好于BP神经网络模型的推荐。

4　总结

本文基于抽样的方法，依据获取的人体特征部位尺寸数据和服装对应的部位尺寸数据，构造了一个合身度评价函数，根据该函数我们结合获取的人体特征部位数据建立了一个针对某款女衬衫的服装号型推荐库。另外一方面，我们利用建立好的服装号型推荐库，创新地采用SVM模型对服装进行号型推荐，并通过与BP神经网络模型的对比发现SVM分类模型更加准确，稳定性也更高。首先，SVM评估模型能够在历史数据积累较少，评估量较多的情况下准备率比较高，降低错误推荐的概率。其次，SVM的鲁棒性比较好，学习泛化能力比较强，有助于推广。最后SVM模型在对推荐号型进行分类的时候，预测准确率比BP神经网络高。因此，对于目前网上购衣遇到困惑的消费者来说，此模型能为他们提供一个借鉴性的帮助，该模型也将进一步挖掘电子商务在服装类商品销售中的潜力。

[1] 于晓坤,王建萍. 人体体型与服装号型的匹配关系及其在电子商务中的应用[J].东华大学学报:自然科学版,2003,01: 43-57,76.

[2] 东苗,郝矿荣,丁永生. 基于模糊神经网络的服装号型推荐专家系统[J].微型电脑应用,2010,03: 21-23,26,69-70.

[3] Vapnik V N. Estimation of Dependencies Based on Empirical Data[M]. Berlin: Springer-Verlag,1982.

[4] Hsu C.W,Lin C J. A comparison of Methods for muti-class support vector machines[J]. IEEE Transactions on Neural Networks,2002,13(2): 415-425.

[5] 王璇. 服装放松量的分析研究[J].纺织学报,2005,04: 126-128.

[6] 许轶超,丁永生. 服装合体性评价的研究方法与应用进展[J]. 纺织学报,2007,10:127-130.

[7] 齐志泉,田英杰,徐志洁. 支持向量机中的核参数选择问题[J]. 控制工程,2005,04:379-381.

Construction of Clothing Size Recommendation Model Based on SVM

Mao Lianzhong1，Hao Kuangrong1，2，Ding Yongsheng1，2
(1.College of Information Sciences and Technology,Donghua University,Shanghai 201620,China; 2. Engineering Research Center of Digitized Textile and Apparel Technology,Ministry of Education,Donghua University,Shanghai 201620,China)

In order to supply a convenient and efficient way of recommending the garment size for the consumers,a way based on support vector machine to construct a model of the size recommending system was designed and proposed,through this way it can solve the problems when choosing the clothing size. Firstly,on the basis of human feature size information and feature size information of clothing,define a garment fit assessment function to obtain suitable size for people with different figure,so it can construct a size categorization database. Then adopt a classification method based on support vector machine to verify the database. Compared to the model of BP neural network,it is found that the recommending accuracy of the model of support vector machine is higher,so it can prove that choosing the model of support vector machine is better way to recommend the clothing size.

Garment Size; Support Vector Machine; Garment Fit; Size Categorization; Neural Network

TP391.4

A

1007-757X(2016)03-0001-04

国家自然科学基金资助项目（61134009）；长江学者和创新团队发展计划资助项目（IRT1220）；上海市优秀学术带头人计划资助项目（11XD1400100）；上海领军人才专项资金资助项目；上海市科学技术委员会重点基础研究资助项目（13JC1407500），11JC1400200）；上海市教育委员会科研创新项目（14ZZ067），中央高校基本科研业务费专项资金资助。

毛连忠（1990-），男，上饶人，硕士研究生，研究方向：模式识别、智能系统，上海，201620郝矿荣（1964-），女，石家庄人，东华大学信息科学与技术学院，博士，教授，博士生导师，研究方向：机器视觉、模式识别、智能机器人、智能控制等研究，上海，201620丁永生（1967-），男，怀宁人，东华大学信息科学与技术学院，博士，教授，博士生导师，研究方向：智能系统、网络智能、DNA计算、人工免疫系统、生物网络结构、生物信息学、数字化纺织服装、智能决策与分析等研究，上海，201620

（2015.10.13）