USM转速全系数自适应控制仿真研究

尤冬梅 董慧敏

（鹤壁汽车工程职业学院，河南 鹤壁 458000）

USM转速全系数自适应控制仿真研究

尤冬梅 董慧敏

（鹤壁汽车工程职业学院，河南 鹤壁 458000）

超声波电动机（USM）运行机理复杂，准确的特征模型很难建立，增加了系统动、静态的控制难度。该文基于特征模型构建了全系数自适应控制策略，控制器只需简单调节参数。仿真结果表明了控制器的有效性。

USM；全系数；自适应

目前，USM控制已经形成了两种局面：一方面，对于控制性能要求低的应用场合，首要选择常规PID控制；主要归功于常规PID比较成熟，设计成本低。另一方面，则是对于高性能的应用场合，这个时候系统的控制策略应该能够自适应。也就是说能够实时跟随USM的实时变化来修改控制策略。这种适当设计控制形式，可以明显提高系统的鲁棒性。但是，通常该种控制律的计算复杂度比常规PID大得多，这也就提高了成本。因而，在线计算量尽量小的有效自适应控制规律是 USM系统控制探究的重要课题。

全系数自适应控制方法是由吴宏鑫院士提出的，是对于一类参数未知线性（或慢时变）控制对象的自适应控制理论[1]。在该控制律设计中包括黄金分割自适应控制策略、逻辑积分控制策略、逻辑微分控制策略、维持/跟踪控制策略等四部分组成。

黄金分割自适应控制策略：在特征模型的基础上，将黄金分割比例（系数 L1=0.382、L2=0.618）与自适应规律相结合的一种新型控制器的设计方法。逻辑积分控制策略：在输出误差及误差变化率的基础上，再根据它们之间的关系自动切换控制策略。该控制策略能消除稳态误差，同时，能保证系统的动态品质。逻辑微分控策略：该策略具有自动增减微分的能力，按系统的要求而定。该控制策略能提高稳态精度，并且不影响动态品质，且能防止超调量。维持或跟踪控策略：该策略与参考模型类似，始终保持输出为一恒定值或跟踪某一输出曲线的输出值。以上四部分控制策略视场合进行选择性的应用[2-3]。

本文对超声波电动机（USM）转速的控制采用的是黄金分割自适应控制策略和逻辑积分控制策略的组合，同时还加入了跟踪控制策略。

1 全系数自适应控制策略的设计

1.1 特征模型

经实验研究，频率-转速特征模型如式（1）所示。

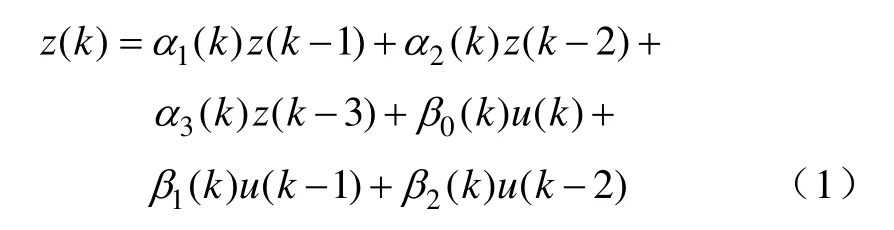
式中，z(k)=yr(k)-y(k)为转速误差；y(k)为USM系统转速；yr(k)为参考转速；u(k)为控制频率；α1(k)、α2(k)、α3(k)、β0(k)、β1(k)、β2(k)为变化的系数，初值为[-1.23 0.226 0.112 11.167 -19.28 8.11]。

1.2 全系数自适应控制律的设计

1）黄金分割自适应控制策略

根据特征模型（1），可设计黄金分割自适应控制策略如下[4]

式中，α1(k)、α2(k)、α3(k)、β0(k)、β1(k)、β2(k)为式（1）的变化系数；L1=0.382，L2=0.618为黄金分割系数；z(k)=yr(k) -y(k)为转速误差；ug(k)为控制频率。

为了得到更高性能的控制器，尝试以下非线性黄金分割自适应控制策略[5]

式中，η1=0.2、η2=0.3、μ =0.8，其余同式（2）。

2）逻辑积分控制策略

逻辑积分的控制策略如下

式中，z(k)=yr(k) -y(k)，k2＞k1＞0，ci一般分为3种情况1，0，-1。

当误差z(k)正向增大，z(k) -z(k -1)＞0，则需加强积分量使误差降低，应取ki等于k2；当 z(k)误差为正但数值开始下降，应当减小k2，取ki等于k1；当 z(k)负向增大，而 z(k) -z(k -1)＜0，需加大积分量使误差值增大，取ki等于k2；z(k)为负值时，虽为负值，但z(k)值开始上升时，积分系数应适当减少，即ki等于k1。

ci值可选为1或0，需要积分时选为1，不需要积分时选为0。出现误差且误差增大时，逐渐累计误差，利用积分控制来减小误差，即 z(k) -z(k -1)＞0时，ci=1；误差减小时，就要适当的减小积分作用，或者使积分控制不起作用，即 z(k) -z(k-1)≤0时，ci=0。

3）跟踪控制策略

跟踪控制采用结构如下，

全系数自适应控制的系统框图如图1所示。图1中yr(k)为给定转速值，y(k)为USM系统输出转速值，z(k)=yr(k) -y(k)为转速误差；u(k)为控制量。

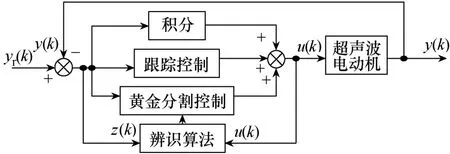
图1 全系数自适应控制系统框图

2 仿真结果对比与分析

图中的黄金分割控制分别采用式（2）和式（3）。根据分析k1的值可取为0，对整个控制律来说，需要确定的值有k2。

2.1 黄金分割自适应控制

根据上述内容，当采用黄金分割自适应控制USM系统时，调节k2，结果见表1。

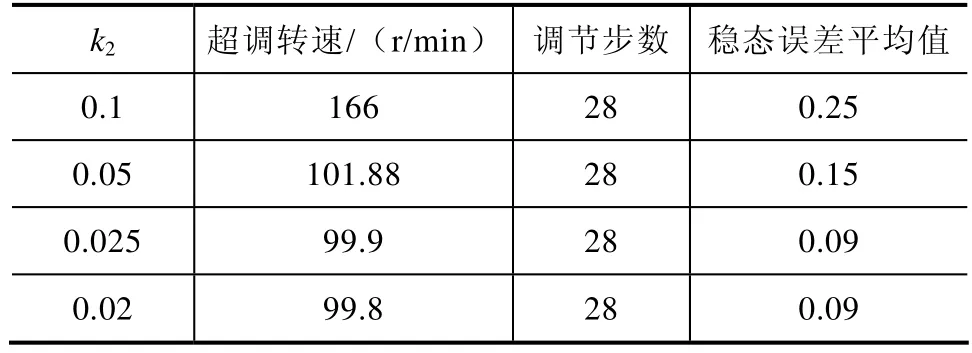
表1 控制器参数的调节过程（90r/min）

由表1可知，改变k2可减小超调量，稳态的误差也相应减少了，k2取0.02。Nref=90r/min，20r/min的仿真结果如图2、图3所示。

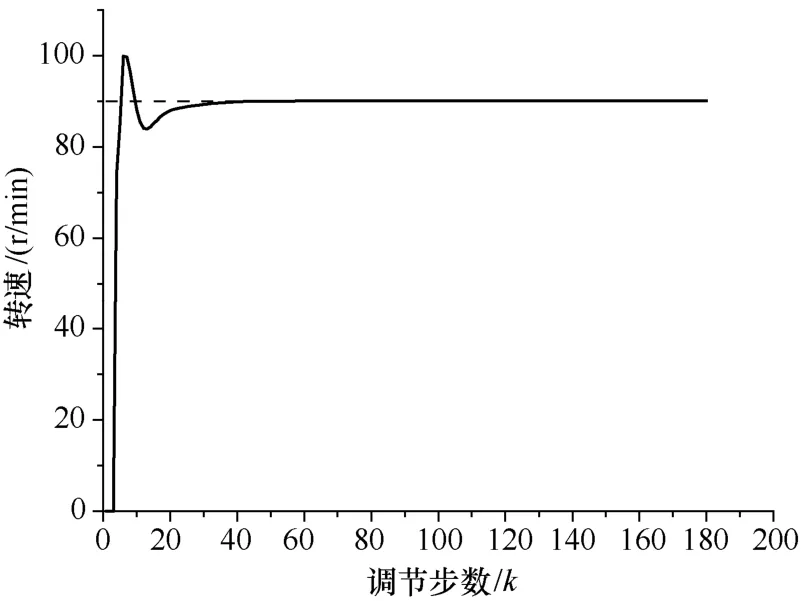
图2 仿真结果与给定转速对比（Nref=90r/min）

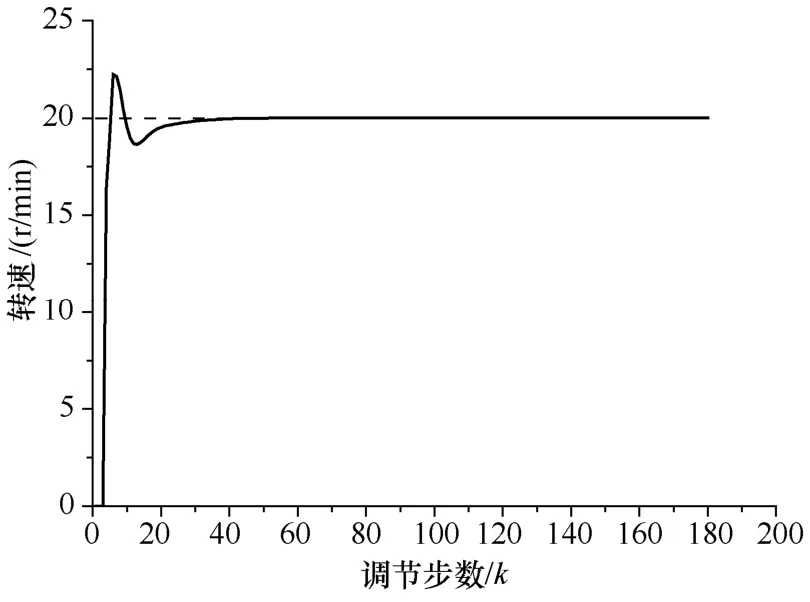
图3 仿真结果与给定转速对比（Nref=20r/min）

2.2 非线性黄金分割自适应控制

根据上述内容，当采用非线性黄金分割自适应控制USM系统时，调节k2，结果见表2。

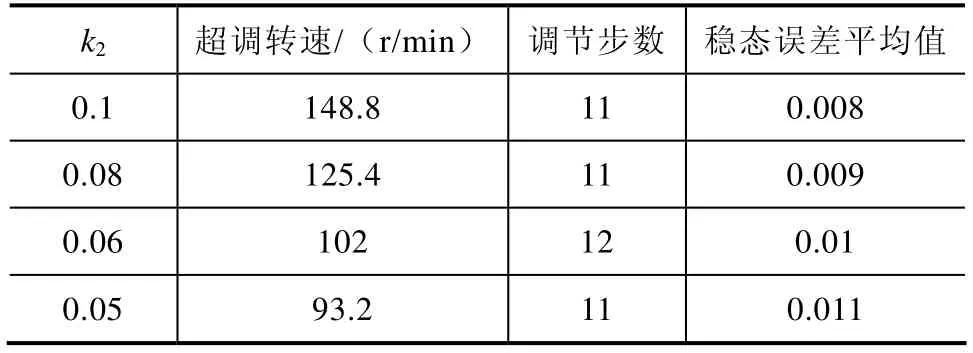
表2 控制器参数的调节过程（90r/min）

由表2可知，改变k2同样有助于减小超调量，稳态的误差有所改善，调节步数有一定的影响，k2取0.05。Nref=90r/min，20r/min的仿真结果如图4、图5所示。

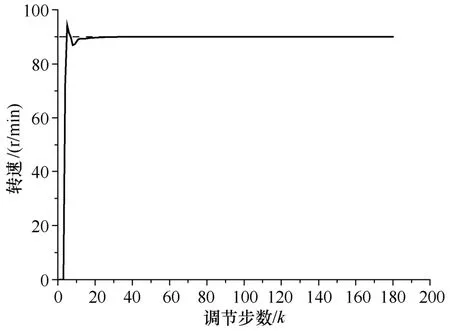
图4 仿真结果与给定转速对比（Nref=90r/min）

为了说明全系数自适应控制的优越性，以下做出了与模型参考自适应的对比分析。

Nref=90r/min时，全系数自适应控制比模型参考自适应控制调节步数减少了 16步，稳态误差也从0.09r/min降为0.01r/min，超调量也变小。可见，全系数自适应控制的调节过程很快，而且稳态精度高。与模型参考自适应控制相比，全系数自适应控制有明显的优越性。

图5 仿真结果与给定转速对比（Nref=20r/min）

图6 仿真结果与给定转速对比（Nref=90r/min）

3 结论

由以上仿真结果可知，两种控制器均存在超调，与线性全系数控制相比，非线性全系数控制所有转速超调有所降低。高转速时，阶跃响应调节步数均降为11步左右，误差在0.01r/min上下波动。Nref= 20r/min的低速区域，调节时间为0.286s，稳态误差值为0.03r/min。可见，高、低转速的控制效果良好，且性能较为接近。两种控制方法调试方便且鲁棒性好，均能达到较好的控制性能。

[1]吴宏鑫, 胡军, 解永春.基于特征模型的智能自适应控制[M].北京: 中国科学技术出版社, 2009.

[2]王勇.全系数自适应控制器若干稳定性质分析[J].空间控制技术与应用, 2012, 38(2): 10-16.

[3]王丽娇.基于对角回归神经网络的自整定全系数自适应控制器及其特征参量辨识[J].航天控制, 2011, 29(5): 15-21.

[4]杨扬, 吴宏鑫.基于特征模型的全系数自适应控制系统稳定性研究[J].航天控制, 2007, 25(5): 3-6.

[5]吴宏鑫, 王颖, 解永春.非线性黄金分割自适应控制[J].宇航学报, 2002, 23(6): 19-26.

Simulation of Ultrasonic Motor’s Entire Coefficient Adaptive Speed Control

You Dongmei Dong Huimin
(Hebi Automotive Engineering Professional College, Hebi, He’nan 458000)

The exact model of Ultrasonic Motor is difficult to establish due to the complex mechanism, this increases the difficulty of the dynamic and static control.In this paper, a entire coefficient adaptive speed controller is designed based on the characteristic model, the controller adjust parameters simply.The experiments indicate the availability of the proposed control strategy.

ultrasonic motor; entire coefficient; adaptive

尤冬梅（1985-），女，河南西华人，助教，主要研究方向为电动机运动控制技术。