移相全桥电路的小信号建模与仿真
2016-11-12翁传辉蔡逢煌
翁传辉 蔡逢煌
(福州大学电气工程与自动化学院,福建 350108)
移相全桥电路的小信号建模与仿真
翁传辉 蔡逢煌
(福州大学电气工程与自动化学院,福建 350108)
小信号模型对于研究变换器的动态特性,变换器各元器件参数的设计有着十分重要的作用。本文从Buck电路出发,结合了移相控制以及零电压开关的原理,建立了移相全桥变换器的小信号模型。并通过对该电路的传递函数的幅频相频特性的分析,验证了该模型的正确性。
ZVS;移相全桥DC/DC变换器;小信号模型
近些年来,移相全桥零电压开关PWM变换拓扑由于其自身的优点,受到了人们的广泛关注与研究。该拓扑通过利用功率开关管的结电容以及变压器的漏感进行谐振,从而使开关管工作在零电压开关(ZVS)状态下。ZVS能够减少开关损耗以及开关应力,并且能够简化缓冲器的设计,能够大大降低成本。开关损耗的降低能够提高电路的工作频率,从而提高电路的功率密度。
小信号模型是研究电力电子变换器的动态性能的有力工具,所以对移相全桥电路进行小信号建模有十分重要的意义。文献[1]中介绍了一种基于状态平均方程的小信号状态空间建模方法;文献[2]比较Buck电路与移相全桥电路的区别,建立了移相全桥小信号模型,并设计反馈补偿网络来改善变换器的特性。本文从Buck模型入手,在简要分析了电路的原理后,详细介绍了移相全桥电路小信号建模的过程。最后建立了移相全桥电路的传递函数,并通过Matlab仿真验证了模型。
1 移相全桥的工作原理
图1给出了移相全桥变换器的电路拓扑,S1与S3为超前桥臂,S2与S4为滞后桥臂,为了实现零电压开关,滞后臂与超前臂开关时间相差一个移相角,这边是移相控制。该工作方式让功率开关管的结电容谐振放电,使得功率开关管的反并联二极管先于功率开关管导通,从而实现功率开关管的零电压开通。

图1 移相全桥变换器电路拓扑
图2给出了电路的主要参数的波形,I为原边电流,VAB为原边电压,VS为副边电压。其工作原理在很多文献都有详细讨论[3],这里不再赘述。
移相全桥本质上是一个Buck电路,但是由于变压器漏感的存在,其电路在工作中存在占空比丢失现象,也就是原边承受方波电压时,由于副边支路上电感的存在使得副边处于续流状态,原边无法向输出端提供能量,反映为副边占空比较原边为小,而副边占空比为电路的有效占空比[4]。有效占空比可以表示为

式中,D为控制输出占空比;ΔD为丢失的占空比。在这里假设输出滤波电感很大,故电路处于导通态时,电流基本保持不变,即图中I1近似等于IP。从图2中,可以得出ΔD可以表示成

则有效占空比则为

从式中可以得出,有效占空比 Deff与输入电压Vin和输出电压匝比开关周期TS、输出滤波电感电流IL、输出滤波电感Lf以及占空比D均有关。
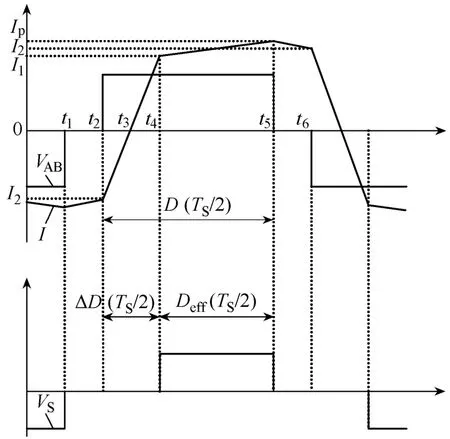
图2 移相全桥变换器主要电路参数波形
2 移相全桥变换器小信号模型的建立
2.1 Buck变换器的小信号模型
由于移相全桥变换拓扑的小信号模型从本质上来说是从Buck变换器小信号模型演化而来的,图3给出了Buck变换器的小信号模型[5]。
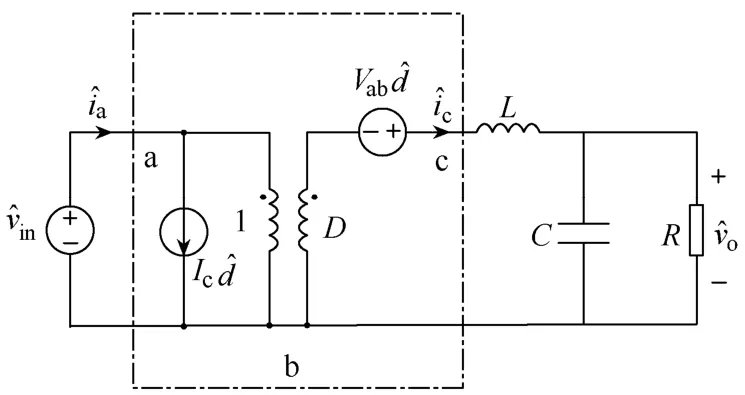
图3 Buck电路小信号模型
因为移相全桥电路的存在占空比丢失现象,所以移相全桥电路的小信号模型应与上模型有所区别。从式(3)中可以看出,当确定了电路拓扑的硬件,可以变化的量只有输入电压Vin、输出滤波电感电流 IL、以及占空比D。则设有效占空比的小信号扰动为则有

2.2 滤波电感的扰动对有效占空比的影响
图4给出了滤波电感的扰动对有效占空比的影响的示意图。如果在电路处于稳态时(实线),给滤波电感电流加一个大小为的扰动,原边电流的变化曲线将如同虚线所示。从图中可以看出占空比丢失现象变得更为恶劣了。其中:

将Δt1对有效占空比的影响则为那么有

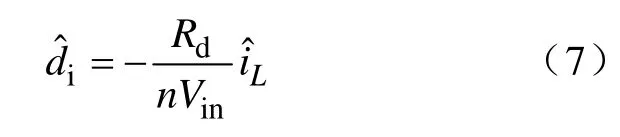
负号表示当滤波电感电流增大时,有效占空比减小。
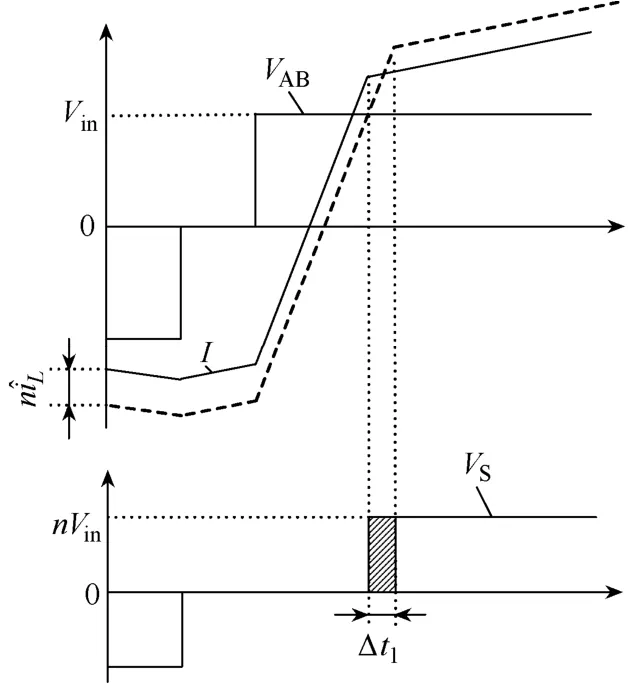
图4 滤波电感的扰动对有效占空比的影响

图5 输入电压的扰动对有效占空比的影响
2.3 输入电压的扰动对有效占空比的影响
图5给出了输入电压的扰动对有效占空比的影响的示意图。如果在电路处于稳态时(实线),给输入电压加一个大小为的扰动,则输入电压的变化曲线将如同虚线所示。从图中可以看出,原边电流的上升斜率增加了,从而副边的电流能够更快增大到负载电流IL的数值,因此,对占空比丢失现象有所改善。其中:
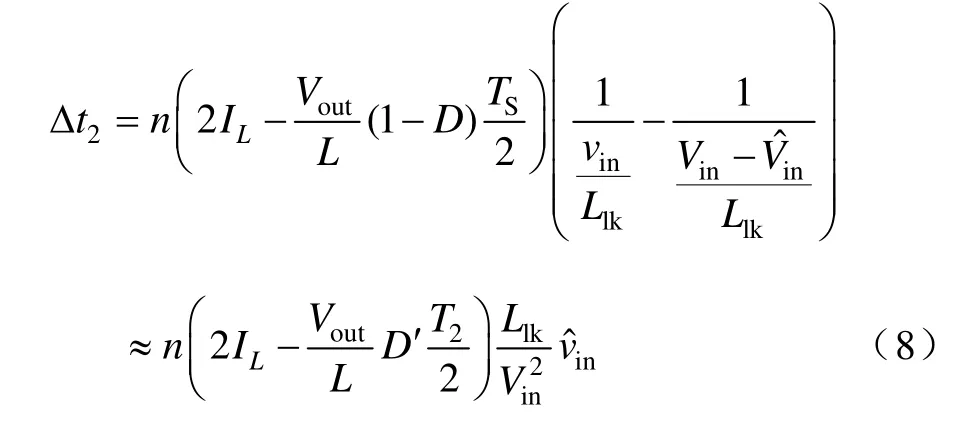
将Δt2对有效占空比的影响记为则

因为变换器的原边存在环流现象,所以为了尽可能得减少导通损耗,D′应尽可能得小。正因为如此,变换器一般工作在深度连续状态下,此时可以认为D′为零。此时

当电路不是处于深度连续,或者处于断续模式下,则应当用式(8)。以下计算分析中,如未特殊说明,则认为电路处于深度连续状态下。
2.4 移相全桥变换器的小信号模型
通过对各扰动进行的分析与计算,可以建立移相全桥变换器的小信号模型如图6所示。

图6 移相全桥变换器小信号模型
3 移相全桥变换器传递函数的建立
由图6可以得出以下公式:
输出滤波器的传递函数:

输出滤波器的输入阻抗:

所用的电路参数:Vin=600V;Vout=360V;fs= 60kHz;Llk=52μH;L=315μH;C=5μH;R=70Ω。
控制到输出电压的传递函数[6]:
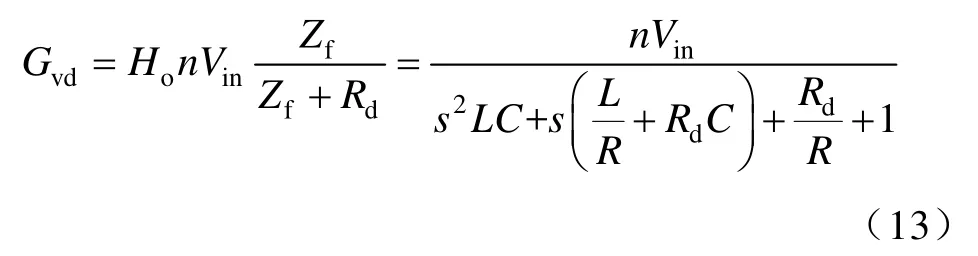
图7给出了Buck变换器与移相全桥变换器控制到输出电压的传递函数。从图中可以看出在低频部分移相全桥变换器的增益较Buck变换器有所下降,这段区域的其实是由Rd/R引起的,也是占空比丢失的原因。因为Rd/R一般为0~0.5,一般取0.25。为了能够进一步定量分析该现象,假设(Rd/R)+1≌1。在式(13)分子分母同乘可以得到
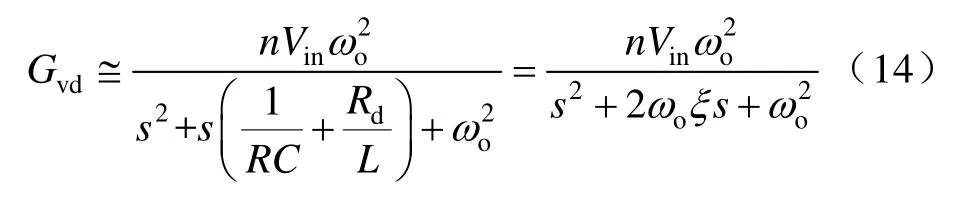
ξ 为2阶阻尼系数:
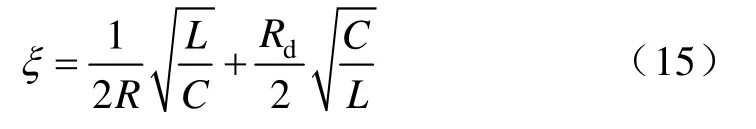
在阻尼系数中第一部分为Buck电路固有的,而第二部分是由漏感引起的,并且这一部分不可忽略。图8给出了移相全桥变换器Rd/R从0变化到0.5的控制到输出传递函数的伯德图。从图中可以看出,Rd/R越大,系统的增益损失越多。与实际漏感越大,占空比丢失越严重相符。

图7 Buck变换器与移相全桥变换器的控制到输出传递函数

图8 Rd/R取不同值时的控制到输出传递函数
4 结论
移相控制以及漏感的应用,对移相全桥变换器的动态特性的改善有着十分重要的影响。变换器的变压比不仅仅由控制决定,和输入电压与负载电流均有关系。由于这些因素的影响,Buck电路的小信号模型不能直接照搬来给移相全桥变换器使用。
文中提出了一种移相全桥变换器的小信号模型。移相控制以及漏感的作用通过与作用在模型上。通过在Buck电路小信号模型添加了两个受控源来实现移相全桥变换器的小信号模型。最后通过Matlab仿真验证了模型的正确性。
[1]Török L, Munk-Nielsen S.Digital fuzzy logic and PI control of phase-shifted full-bridge current-doubler converter[C]//Telecommunications Energy Conference (INTELEC), 2011 IEEE 33rd International.IEEE, 2011: 1-7.
[2]孙琳, 曹以龙.移相全桥零电压变换器的建模与控制[J].上海电力学院学报, 2014, 30(4): 329-332, 345.
[3]Lin L, Zhong H, Deng Y, et al.Analysis, design and implementation of phase-shifted series resonant high-voltage capacitor charging power supply and its fuzzy logic controller[C]//Energy Conversion Congress and Exposition (ECCE), 2014 IEEE.IEEE, 2014: 884-891.
[4]Aboushady A A, Ahmed K H, Finney S J, et al.Discrete time domain small-signal modeling of full-bridge phase-shifted series resonant converter[C]//Energy Conversion Congress and Exposition (ECCE), 2010 IEEE.IEEE, 2010: 2019-2024.
[5]徐德鸿.电力电子系统建模及控制[M].北京: 机械工业出版社, 2006.
[6]Jiang W, Hu R, Zhang J.The PWM phase-shifted plus feed-forward control of the boost converter applied in supercapacitor energy storage system[C]//Electrical and Control Engineering (ICECE), 2011 International Conference on.IEEE, 2011: 455-458.
Small-signal Modeling and Simulation on Phase-shift Full-bridge Converter
Weng Chuanhui Cai Fenghuang
(College of Electrical Engineering and Automation, Fuzhou University, Fuzhou 350108)
Small-signal model plays a very important role for the study of the dynamic characteristics of the converter and the design of component parameters of the converter.From the Buck circuit, combined with phase shift control and the principle of zero voltage switching, the small-signal model of phase-shift full-bridge converter has been built.The magnitude-frequency and phase-frequency characteristics of small-signal transfer function have been analyzed, and the result of the simulation verifies the correctness of the model.
ZVS; phase-shift full-bridge DC/DC converter; small-signal model
