简并破却项对反式聚乙炔中极化子单激发态的影响

陈少波　常刘安　陈英　张殿喜

（1.安顺学院电子与信息工程学院，贵州　安顺　561000；2.重庆大学物理学院凝聚态物理研究所，重庆　401331）

简并破却项对反式聚乙炔中极化子单激发态的影响

陈少波1常刘安2陈英1张殿喜1

（1.安顺学院电子与信息工程学院，贵州安顺561000；2.重庆大学物理学院凝聚态物理研究所，重庆401331）

本文采用紧束缚模型加上长程电子关联项哈密顿量模型，研究了反式聚乙炔中极化子的单电子激发，分析了其单激发态的物理性质。与极化子相比，其单激发态体系能带中央的两条定域能级相互靠拢，近乎重合，形成了束缚较弱的孤子-反孤子对。此外，研究简并破缺参数对极化子单激发态反向极化的影响发现，基态简并聚乙炔中的极化子单激发态的反向极化最强，随着te的增大反向极化减弱，当te增大到一定值时，反向极化消失。

极化子；单激发态；长程电子关联；简并破缺

自20世纪70年代Heeger等科学家发现反式聚乙炔掺杂后导电率可以大大提高，变成良导体［1］以来，高分子共轭聚合物作为一类具有广泛应用前景的有机合成材料，越来越受到人们的广泛关注［2-5］。导电高分子聚合物是准一维体系，具有低维不稳定性［6，7］，其中的共轭π电子云具有较强的非局域和极化特性，从而使这类材料在电、磁、光等方面具有不同于传统半导体或金属的独特性质。通过对其导电机理的深入研究，人们发现导电高聚物的载流子不再是传统的电子或空穴，而是由于电子-晶格相互作用所产生的带电元激发，如孤子、极化子和双极化子等［8］，理论和实验都对这些载流子的性质进行了大量的研究，并且取得了一系列有意义的成果［9］。

然而，对共轭聚合物的研究，多数只是停留在对基态的讨论，对于它们的单激发态，人们还不是很清楚，本文将在前人工作的基础上，采用SSH模型［10］和长程电子关联项，在自然边界条件下进一步研究了反式聚乙炔中极化子单激发态在电场下的极化行为，并探讨了简并破缺参数对其极化程度的影响。

1　模型和方法

对于准一维聚乙炔链，采用SSH模型和长程电子关联项来描述，体系的总哈密顿量为：

式（1）中，HSSH是SSH哈密顿量，描述晶格和电子相互作用、格点动能和势能。

式（2）中，t0是电子在近邻晶格之间的跃迁常数；α是电子-晶格耦合常数［11］；为第n个格点上自旋为s的电子产生和湮灭算符；te是对称破缺参量，反映基态非简并性［12］；un为碳原子偏离平衡位置的位移。H′是为了防止链的塌缩［11，13］而引入的项。

HE是当聚合物处于外电场E中时各格点上的电子与此外电场的相互作用势能：

He-e是电子电子相互作用哈密顿量，由扩展的Hubbard模型［6，7］给出：

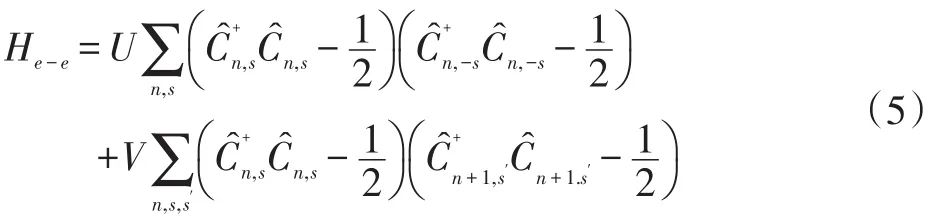
式（5）中，U是同一格点上的不同自旋电子之间的相互作用，V是相邻格点之间的相互作用。常数项1/2来源于每一个格点上电子自旋向上和向下的几率各占1/2。计算中，电子电子相互作用He-e用Hartree-Fock进行分解。

长程电子关联效应由下面关联哈密顿量［6］确定：

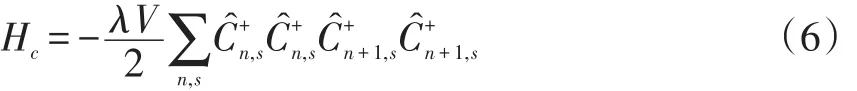
λ在计算中取1/2。

令φn=（-1）nun，利用能量最低原理，采用量子力学的微扰论把体系的总能量在平衡位置附近展开，令其一阶项的系数为0，得到格点平衡条件为：

式（7）中［14］，。

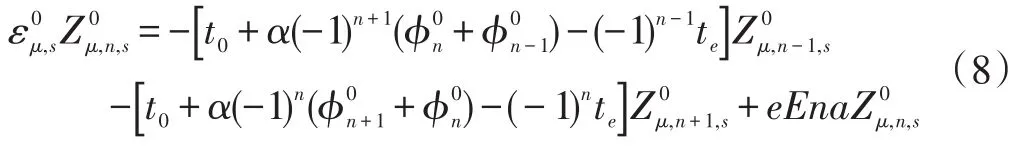
迭代求解方程（7）和（8）可以得到体系的晶格位形分布、电子能级及其波函数、格点净电荷密度分布。

2　结果和讨论

图1　极化子晶格位形

对于反式聚乙炔，选取参数：t0=2.5eV，α=41eV/nm，a=0.122nm，K=2 100eV/nm2，K′=-51.263eV/nm，te=0eV，U=2V=0.5eV，链长取100个格点。在准一维聚乙炔链中，当掺入杂质时，体系就会因为电子-晶格相互作用而形成稳定的极化子（见图1）。根据得失电子的情况，极化子可以分为空穴极化子和电子极化子两种，此时，体系能带的中央出现了两条定域的极化子能级εu和εd，图2（a）和（b）分别是空穴极化子和电子极化子的能谱和电子分布示意图。

图2　极化子的能谱和电子分布示意图

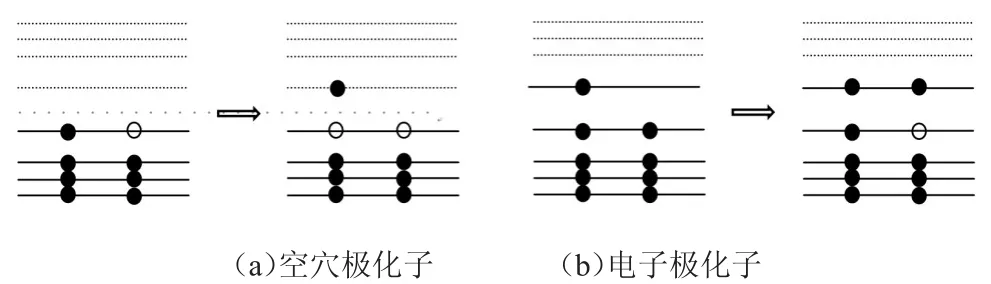
图3　极化子单电子激发的电子跃迁示意图

2.1反式聚乙炔中的极化子的单激发态

单电子激发是指有一个电子吸收能量从低能级跃迁到高能级。当极化子的εd上的电子获得能量跃迁到εu上，就是极化子的一种单电子激发，如图3分别是空穴极化子和电子极化子单电子激发的电子跃迁。

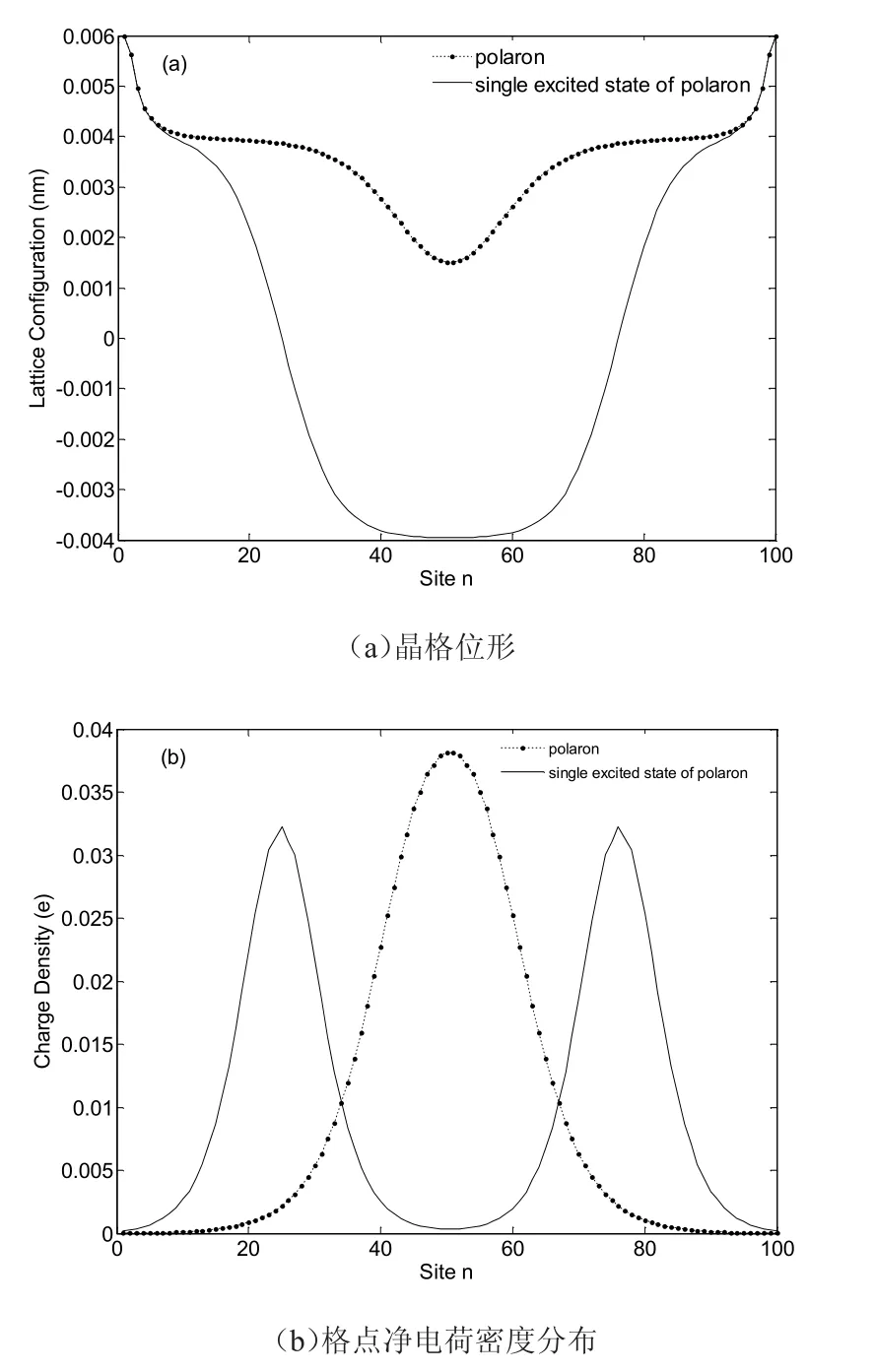
图4　电子极化子及其单激发态

考虑到电子极化子和空穴极化子是对称的，本文中只考虑电子极化子。按照图3（b）的电子跃迁方式发现，极化子单激发态的晶格位形A、B相分明，形成了束缚较弱的孤子-反孤子对；格点净电荷密度也随之发生变化，单峰劈裂为左右对称的等高双峰，它们各带半个负电荷，如图4所示。

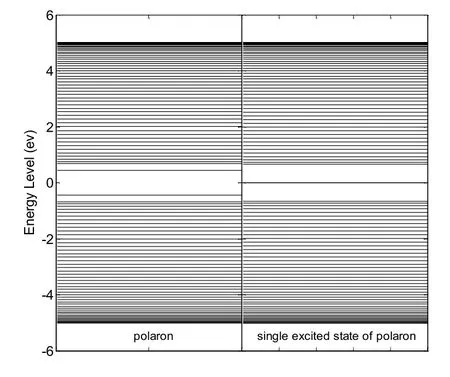
图5　反式聚乙炔极化子和极化子单激发态的能谱

对于晶格缺陷发生变化的极化子单激发态，其能级结构也相应地发生变化，两条定域能级相互靠拢，近乎重合，如图5所示。通过计算得到：对于反式聚乙炔，极化子的两定域能级差为0.892 9eV；而极化子单激发态的定域能级差却为0.003 3eV［可以近似把±0.001 65认为是孤子（反孤子）能级］。

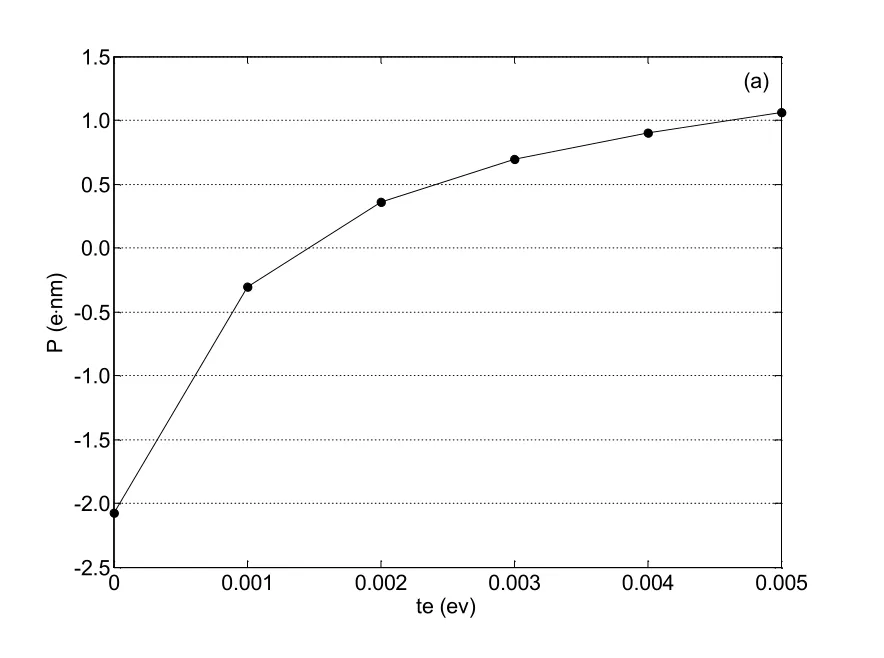
图6　电子极化子单激发态的电偶极矩随简并破缺参数te的变化

图7　不同简并破缺参数下的格点净电荷密度分布

2.2简并破缺参数对电子极化子单激发态反向极化的影响

考虑到大多数聚合物都是基态非简并的，详细探讨了简并破缺参数te对极化子单激发态的影响。图6给出了E=1.0×104V/cm时，电子极化子单激发态体系的电偶极矩与te的关系。由图6可知，只有简并破缺参数很小时，体系才会出现反向极化现象。基态简并的极化子单激发态体系的反向极化最强，te增大，反向极化减弱，如图7所示；当te增大到一定值时，体系呈现正向极化。对应的体系电荷转移量（见表1）也说明了这一现象。

3　结论

反向极化是有机共轭聚合物一种奇特的性质，本文研究了聚乙炔中电子极化子的单激发态，发现电场作用下，极化子单激发态出现反向极化。但是，这种现象通常只存在于弱电场下，在弱电场范围内，加大电场，反向极化会增强。电场较强时，体系出现正向极化，随后正向极化程度增强，反向极化程度减弱至消失；当电场达到临界值时，单激发态被解离。而且，极化子单激发态的反向极化现象只出现在基态简并或者简并破缺参数较小的体系中。基态简并聚乙炔中的极化子单激发态的反向极化最强，随着te的增大反向极化减弱，当te增大到一定值时，反向极化消失。

表1　对应的体系电荷转移量

［1］Chiang CK，Fincher CR，Park YW，et al.Electrical Conductivity in Doped Polyacetylene［J］.Physical Review Letters，1977（17）：1098-1101.

［2］Shukla A，Mazumdar S.Designing emissive conjugated polymers with small optical gaps：a step towards organic polymeric infrared lasers［J］.Phys.Rev.Lett.，1999（19）：3944-3947.

［3］Gontia L，Frolov SV，Liess M，et al.Excitation dynamics in disubstituted polyacetylene［J］.Phys.Rev.Lett.，1999（20）：4058-4061.

［4］Burroughes JH，Bradley DDC，Friend RH，et al.Lightemitting diodes based on conjugated ploymers［J］.Nature，1990（6293）：539-541.

［5］Gustafsson G，Cao Y，Treacy GM，et al.Flexible lightemitting diodes made from soluble conducting polymers［J］.Nature.，1992（6378）：477-479.

［6］Heeger AJ，Kivelson S，Schrieffer JR，et al［J］.Sohtons in conducting p olymers［J］.Rev.Mod.Phys.，1988（60）：781-850.

［7］Friend RH，Bradley DD，Townsend PD.Photo-excitation in conjugated polymers［J］.Journal of Physics D：Applied Physics，1987（11）：1367.

［8］Mizes HA，Conwell EM.Stability of polarons in conducting polymers［J］.Phys.Rev.Lett.，1993（70）：1505-1508.

［9］Mcgehee MD，Miller EK，Moses D，et al.Advances in Synthetic Metals：twenty years of progress in science and technology［M］.Elsevier，Lausanne：Elsevier Science，1999：98.

［10］Su WP，Schrieffer JR，Heeger AJ.Soliton excitations in polyacetylene［J］.Phys.Rev.B，1980（22）：2099-2111.

［11］Stafstrom S，Chao KA.Polaron-bipolaron—soliton doping in polyacetylene［J］.Phys.Rev.B，1984（4）：2098-2103.

［12］Wang CL，Su ZB，Martino F.Bipolaron dynamics in nearly degenerate quasi-one-dimensional polymers［J］.Physical Review B Condensed Matter，1986（33）：1512-1515.

［13］Su WP.Existence of neutral kinks in polyacetylene［J］. Solid State Communications，1980（11）：899-901.

［14］Kun G，Liu XJ，Liu DS，et al.Reverse polarization in charged蟺-conjugated oligomers［J］.Conference of the Asian Consortium for Computational Materials Science，2005（23）：54-58.

Effect of Degeneracy Breaking Parameters on Single Excited State of Polaron in the Trans-polyacetylene

Chen Shaobo1Chang Liuan2Chen Ying1Zhang Dianxi1
（1.College of Electronic and Information Engineering，Anshun University，Anshun GuiZhou 561000；2.Department of Physics and Institute of Condensed Matter Physics，Chongqing University，Chongqing 401331）

In this paper，physical property of single excited state of polaron in the trans-polyacetylene was investigated theoretically by using the tight-binding SSH model and long range electric correction model.It was found that localized energy levels in the energy gap were closer to each other compared with polaron’s resulting in forming a weaker-binding soliton-antisoliton pairs.In addiction，the effects of degeneracy breaking parameters on polarization inversion of a single excited polaron was studied.It was found that the degree of polarization inversion of single-excited state of polaron in polyacetylene with degenerate ground state was largest and it would decrease with te，polarization inversion would disappear at a critical degeneracy breaking parameter.

polaron；single excited state；long range electric correction；degeneracy breaking parameter

O561

A

1003-5168（2016）06-0136-04

2016-05-08

安顺学院2015年度青年项目（2015AQ08）；贵州省科技厅三方联合科技基金（黔科合LH字［2015］7696号）。

陈少波（1987-），男，讲师，研究方向：有机分子电子学；常刘安（1988-），男，研究方向：有机分子电子学。