PEMFC碳纸气体扩散层内气液两相流格子Boltzmann模拟*
2016-11-10蒋方明
吴 伟,陈 旺,蒋方明
(1. 中国科学院广州能源研究所,广州 510640;2. 中国科学院可再生能源重点实验室,广州 510640;3. 广东省新能源和可再生能源研究开发与应用重点实验室,广州 510640;4. 中国科学院大学,北京 100049)
PEMFC碳纸气体扩散层内气液两相流格子Boltzmann模拟*
吴 伟1,2,3,4,陈 旺1,2,3,4,蒋方明1,2,3†
(1. 中国科学院广州能源研究所,广州 510640;2. 中国科学院可再生能源重点实验室,广州 510640;3. 广东省新能源和可再生能源研究开发与应用重点实验室,广州 510640;4. 中国科学院大学,北京 100049)
为了提高质子交换膜燃料电池(PEMFC)水管理,本文借助多相流格子Boltzmann模型(LBM)模拟分析了PEMFC碳纸气体扩散层(GDL)内的气液两相输运过程,主要研究了GDL疏水性对气液两相流的影响。结果表明:液态水流路径不仅受到GDL结构形态的影响,而且受到材料疏水性影响。液态水在疏水性弱的GDL中不仅容易沁入,而且容易在孔隙中达到饱和;相反,在疏水性较强的GDL中,液态水很难突破沁入小尺寸孔隙,而从孔径较大的孔隙流通,从而形成毛细力主导的指进流动。
质子交换膜燃料电池;伪势多相流格子Boltzmann模型;气液两相输运;碳纸气体扩散层;疏水性
0 前 言
质子交换膜燃料电池(proton exchange membrane fuel cell,PEMFC)内气液两相输运对电池性能和使用寿命具有重要影响,一个突出的问题就是液态水过多积累形成“水淹”,导致催化剂层(catalyst layer,CL)内活性反应点被液态水覆盖、反应物传输路径被液态水阻塞,继而造成燃料电池性能下降、气流流阻增大(泵功增加),同时还可能会造成电池催化层因燃料饥饿(fuel starvation)而致碳腐蚀,加速膜电极组合(membrane electrode assembly,MEA)的老化,给燃料电池的寿命带来灾难性影响。
燃料电池碳纸气体扩散层(gas diffusion layer,GDL)内的气液两相输运过程很难通过实验的手段来观测到,数值模拟可以可视化GDL内部两相输运行为[1-2]。近年来,不少学者用VOF方法[3-4]或VOF与level-set结合的方法[5]研究PEMFC流道气液两相流动,但均难以获得较为满意的结果,其主要原因是 GDL内部微结构十分复杂且孔隙的几何尺寸较小,其内部气液两相流为毛细力主导(毛细数 Ca在10-6量级)的流动[6];VOF数值方法难以处理复杂的多孔介质流动区域边界。具有介观动力学特征的格子Boltzmann方法可以方便地引入分子间相互作用力,自动捕捉相界面。近些年来已有大量关于GDL内部气液两相输运过程的格子Boltzmann方法研究。如:HAO等[7]研究了GDL材料润湿性对液态水输运的影响,发现在相同的毛细数下,强疏水性GDL内的液态水为毛细流动(capillary flow),而接近中性的 GDL内液态水展现出稳定流动的特性(stable displacement);ZHOU等[8]研究了重力、材料润湿性以及凝结对液态水输运的影响;MOLAEIMANESH等[9]研究了GDL材料润湿性在不同方向上的分布对液态水的流动影响,另外,还发现加强GDL疏水性有利于排水,但是当疏水性超过一定程度时,对排水的效果不是很明显;CHEN等[10]研究了GDL润湿特性对液态水的流动的影响,包括 PTFE含量与分布对液态水的分布影响;PARK等[11]模拟了液滴流入多孔GDL的过程。
格子Boltzmann多相模型包括颜色模型[12]、伪势模型[13-16]、自由能模型[17-20]与动力学模型[21]。其中,SHAN等[13]提出的伪势多相流模型(Shan-Chen多相流模型)引入了相邻粒子之间的相互作用势,可以方便地刻画出分子之间的相互作用,已经被广泛地用于模拟复杂多相流体系统。本文将借助伪势多相流模型对 GDL内气液两相输运过程进行数值模拟研究。
1 伪势多相流模型的原理
假设流体中共有S个不同的粒子,则伪势多相流模型包含S个分布函数的演化:

式中,τσ为松弛时间,ei为在i方向上的格子离散速度[22],δt为时间步长,和分别为第σ类粒子在t时刻、位置x处的分布函数和平衡态分布函数。对于包含静止粒子的FHP[23]规则六边形格子或三维的FCHC[24]格子,平衡态分布函数为:
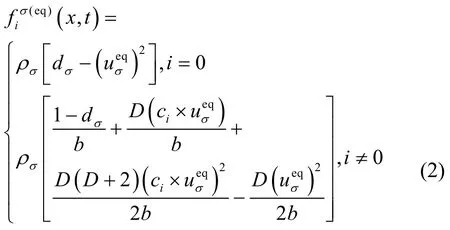
其中,dσ为小于 1的常数,b代表离散速度数,D为空间维数,ci为格子离散速度,为宏观的平衡态速度,ρσ为流体宏观密度,如第σ类的宏观量为:


其中,F为不同粒子间作用力u' 为混合速度,其定义如下:

Shan-Chen伪势多相流模型假设不同流体粒子(如第σ类与第类)之间存在非局部的相互作用,相应的势函数为:



流体与固体之间的作用力也可以类似地表示出来:

其中:s(x')为x'点处是否为固相的判断函数,取1时代表 x'点为固相,取0则x'点为非固相;Gσs表征流体与固相之间的相互作用力强度,定义如下。
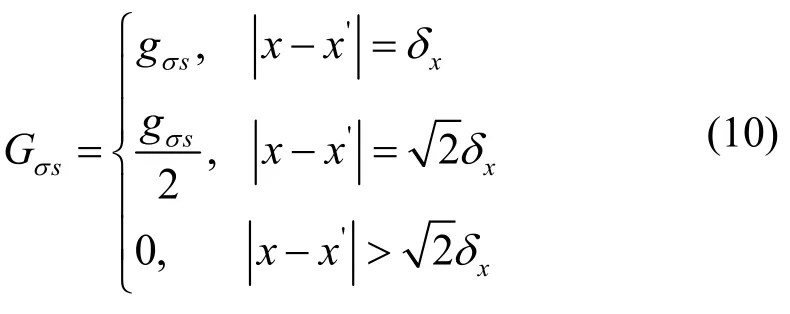
其中,gσs值决定流体与固壁面之间的作用力大小。
2 模型验证
2.1 Laplace定律验证
根据Laplace定律可知,静止在液体内的气泡在力平衡条件下,气泡内外的压力差与表面张力σ以及气泡半径R有关,其关系式为:

其中,σ为表面张力,R为气泡半径,ΔP为气泡内外压差。式(11)表示当流体的相关物性不变时,ΔP与1/R成线性关系,直线斜率表示表面张力。
模拟时,计算参数设置如下:计算区域离散为50×50×50的格子,计算域x、y、z方向相对的两个面上均采用周期性边界条件,初始时刻,半径为R的气泡被置于计算域中心位置;气泡内外两相的密度均为150格子单位密度;粒子间作用力强度分别取g12=0.001和g12=0.0012(下标分别表示1、2类粒子)。图1示出了气泡内外压差与半径之间的关系,从图中可以看出,在不同的粒子间作用力强度下,对应的PΔ与 1/R之间均成线性关系,这与Laplace定律相符,并且直线斜率与作用力强度成正比,作用力强度越大,则斜率越大。
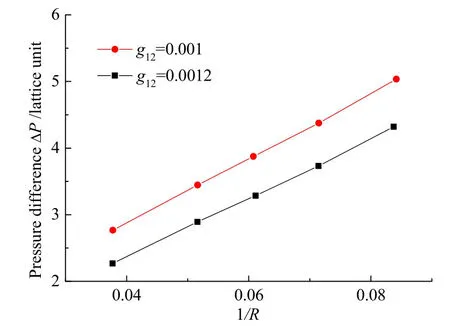
图1 Laplace定律验证Fig. 1 Validated with Laplace’s Law
2.2 静态接触角模拟
润湿角可以反映液-固-气三相之间分子力作用,若液-固-气系统给定,当系统温度和压力一定时,则可确定润湿角。GDL内的纤维一般为疏水性,材料疏水性与亲水性可以表现为水-气-固共存时水在固壁上的接触角,角度越大表示材料的疏水性越强;反之,则材料亲水性越强。
通过调节 Shan-Chen多相伪势格子 Boltzmann模型中的流体粒子与材料壁面之间的相互作用力强度获得不同的接触角。计算域采用50×50×50的格子,z=0与z=49两个平面设置为壁面,采用半步长反弹边界条件,x、y方向均采用周期性边界条件。如图2所示,初始时刻,半径为R的半球形液滴被置于z=0的壁面中心位置;流体粒子间作用力强度为g12=g21=0.001,流体粒子与壁面之间的作用力强度为g1s=-g2s。计算过程中,通过调节流体与壁面之间的作用力强度获得不同的接触角。计算收敛后,接触角θ分别为60°、90°、120°的液滴最终形态如图2所示。

图2 不同接触角θ液滴附着固壁的形态Fig. 2 The simulated shapes of liquid droplet stciking on solid surface of different wetting properties
3 气体扩散层内气液两相输运的LBM模拟
3.1 物理模型

图3 数值重建的气体扩散层Fig. 3 The computer-generated gas diffusion layer
本文采用SCHULZ等[25-27]提出的非交织纤维随机生成技术,重建碳纸GDL介孔微结构。该重建过程的具体实施参见文献[25]。重建时考虑的基本离散单元尺寸为 2.5 μm,整个 GDL层厚度 x方向(through-plane)包括60个单元(150 μm),整个GDL区域的孔隙率设置为0.8,并在GDL出口厚度方向上设置19个单元(47.5 μm)的空腔,用做液态水突破GDL后的积累空间,y、z方向与x方向一样,也分别包含79个单元(197.5 μm)。重建的GDL结构如图3所示。
3.2 初始条件与边界条件
初始时,GDL内部充满气体。x=0为入口,即液态水沁入入口,x=79为出口,进出口采用定压边界,其余周边4个面均为对称边界。考虑3个算例,即接触角为93°、127°、153°。
3.3 计算结果与讨论
图4对比了在相同时刻t不同接触角GDL内液态水的沁入量与方式。不同算例液态水沁入量与方式有所不同,呈现出一定的规律性。接触角越大、液相越难沁入,相同时刻接触角为 93°的算例沁入GDL的液态水明显多于接触角为153°的算例;液态水在毛细力主导的驱动下同时向 x、y、z方向沁入并占据原来充满气体的孔隙,碳纸纤维的阻隔使得液态水出现分化,液态水向前推进,在两相界面遇到多个孔隙时,优先进入孔径较大的孔隙中。这是由于受到GDL结构形态以及材料疏水性影响,疏水性较强的 GDL中液态水突破小孔沁入的可能性更小,导致液态水从孔径较大的孔隙流入。这种流动路径的强选择性对GDL内气体能够快速进入CL有利。因此,我们可以利用GDL疏水性能对液态水路径选择的作用,设计出合适的GDL,一方面可以较好地输运气体反应物,另一方面,还能快速地排出液态水。

图4 GDL内气液两相输运的动态演化Fig. 4 Time-changing liquid saturation distriution in the GDL
为进一步考察 GDL内气液两相输运过程的动态变化,图5给出了x断面上的液态水的平均饱和度。从图中可以看出在同一时刻,接触角越小,GDL内x断面上的液态水的平均饱和度相对较高,且沿着x方向下降的坡度越大,这说明接触角越小,液态水更容易平稳沁入 GDL;时间越长,同一断面上的液态水的平均饱和度越高,这说明GDL内沁入的液态水更多。对比不同时刻的液态水饱和曲线可以发现,接触角为153°与127°的碳纸GDL,厚度方向各个截面液态水饱和度曲线呈现明显的下凹,接触角越大,曲线下凹越厉害;接近中性情况(接触角为93°)的曲线则明显上凸,这也进一步说明中性润湿条件下,液态水流动更稳定趋前。由Laplace定律可知,厌水性孔隙通道内表面张力的作用越弱,阻碍液态水流动的作用也越弱,导致液态水沁入GDL步调相对更一致,即两相界面平稳地向前推进;反之,液态水沁入路线的选择性更强,使得液态水更快地从孔径较大的地方突入GDL内部,在孔径较小的地方阻力较大使得液态水无法突破导致这些地方的沁入受阻,从而形成了以毛细力主导的毛细指进流动。
计算网格大小对模拟结果有一定的影响,通过Richardson外推方法可以检验网格对结果的影响。使用不同格子分辨率3.7 μm、2.5 μm、1.5 μm对同一GDL结构内气液两相流进行模拟,结果表明:以Richardson外推法得到GDL/GC(gas channel)界面的截面平均饱和度精确解与不同格子分辨率时得到的模拟结果误差分别小于9.5%、6%、4.5%;在GDL接触角为93°的算例中,6000δt时上述三种格子分辨率下的GDL/GC界面液态水饱和度分别为0.270、0.261、0.258,验证了模拟结果的可靠性。

图5 x方向上的截面平均液态水饱和度曲线Fig. 5 Profile of x-sectional average liquid saturation
趋向中性的 GDL碳纸材料能够促进液态水形成更多连通的路径,液态水占据更多的孔隙而可能使得反应气体难以进入,但液态水在疏水性强的GDL中的选择性传输使得即便部分液态水由大孔通道连通贯穿GDL达到流道界面,GDL内仍有一定数量的孔隙被气体占据,这部分气体占据的孔隙可能成为反应物气流通道,GDL不至于在短时间内完全被液态水堵死。因此,利用GDL疏水性能对GDL排水的影响设计出合适的 GDL对气体反应物运输与GDL排水具有重要意义。
4 结 论
本文采用Shan-Chen多相LBM模型对GDL内气液两相输运过程进行模拟和分析,结论如下:
(1)模拟证实了气体扩散层内气液两相动态输运过程符合毛细指进流动机制,液态水在疏水性GDL中的流通路径呈现选择性,液体倾向于在GDL各方向上毛细力最小的(孔径最大)孔隙突破形成液体流动通路。
(2)碳纸GDL的润湿性特性对两相输运过程具有重要影响,材料疏水性减弱会使相同孔径下的毛细力减小,将导致液态水的选择性传输倾向减弱,加速了排水。但GDL内大量孔隙(包括较多的小孔径孔隙)被液态水占据而减少了气体通路,有可能会造成电池性能下降。
[1] WANG C Y. Fundamental models for fuel cell engineering[J]. Chemical reviews,2004,104(10): 4727-4766. DOI: 10.1021/cr020718s.
[2] JIANG F M,WANG C Y. Numerical modeling of liquid water motion in a polymer electrolyte fuel cell[J]. International journal of hydrogen energy,2014,39(2): 942-950. DOI: 10.1016/j.ijhydene.2013.10.113.
[3] HIRT C W,NICHOLS B D. Volume of fluid (VOF)method for the dynamics of free boundaries[J]. Journal of computational physics,1981,39(1): 201-225. DOI: 10.1016/0021-9991(81)90145-5.
[4] ZHU X,SUI P C,DJILALI N. Three-dimensional numerical simulations of water droplet dynamics in a PEMFC gas channel[J]. Journal of power sources,2008,181(1): 101-115. DOI: 10.1016/j.jpowsour.2008.03.005.
[5] CHEN S Q,LIAO B. A coupled level set and volume of fluid method for tracking moving interface in multiphase flow[J]. Journal of ship mechanics,2012,16(3): 203-217. DOI: 10.3969/j.issn.1007-7294.2012.03.001.
[6] MUKHERJEE P P,KANG Q J,WANG C Y. Pore-scale modeling of two-phase transport in polymer electrolyte fuel cells-progress and perspective[J]. Energy & environmental science,2010,4(2): 346-369. DOI: 10.1039/B926077C.
[7] HAO L,CHENG P. Lattice Boltzmann simulations of water transport in gas diffusion layer of a polymer electrolyte membrane fuel cell[J]. Journal of power sources,2010,195(12): 3870-3881. DOI: 10.1016/ j.jpowsour.2009.11.125.
[8] ZHOU P,WU C W. Liquid water transport mechanism in the gas diffusion layer[J]. Journal of power sources,2010,195(5): 1408-1415. DOI: 10.1016/j.jpowsour.2009. 09.019.
[9] MOLAEIMANESH G,AKBARI M H. Water droplet dynamic behavior during removal from a proton exchange membrane fuel cell gas diffusion layer by Lattice-Boltzmann method[J]. Korean journal of chemical engineering,2014,31(4): 598-610. DOI: 10.1007/ s11814-013-0282-6.
[10] CHEN L,LUAN H B,HE Y L,et al. Numerical investigation of liquid water transport and distribution in porous gas diffusion layer of a proton exchange membrane fuel cell using lattice Boltzmann method[J]. Russian journal of electrochemistry,2012,48(7): 712-726. DOI: 10.1134/S1023193512070026.
[11] PARK J,LI X. Multi-phase micro-scale flow simulation in the electrodes of a PEM fuel cell by lattice Boltzmann method[J]. Journal of power sources,2008,178(1): 248-257. DOI: 10.1016/j.jpowsour.2007.12.008.
[12] LUO L S. Theory of the lattice Boltzmann method: lattice Boltzmann models for nonideal gases[J]. Physical review e,2000,62(4): 4982-4996. DOI: 10.1103/ PhysRevE.62.4982.
[13] SHAN X W,CHEN H D. Lattice Boltzmann model for simulating flows with multiple phases and components[J]. Physical review e,1993,47(3): 1815-1819. DOI: 10.1103/ PhysRevE.47.1815.
[14] SHAN X W,CHEN H D. Simulation of nonideal gases and liquid-gas phase transitions by the lattice Boltzmann equation[J]. Physical review e,1994,49(4): 2941-2948. DOI: 10.1103/PhysRevE.49.2941.
[15] SHAN X W,DOOLEN G. Multicomponent lattice-Boltzmann model with interparticle interaction[J]. Journal of statistical physics,1995,81(1/2): 379-393. DOI: 10.1007/BF02179985.
[16] SHAN X W,DOOLEN G. Diffusion in a multicomponent lattice Boltzmann equation model[J]. Physical review e,1996,54(4): 3614-3620. DOI: 10.1103/PhysRevE.54.3614.
[17] SWIFT M R,OSBORN W R,YEOMANS J M. Lattice Boltzmann simulation of nonideal fluids[J]. Physical review letters,1995,75(5): 830-833. DOI: 10.1103/ PhysRevLett.75.830.
[18] SWIFT M R,ORLANDINI E,OSBORN W R,et al. Lattice Boltzmann simulations of liquid-gas and binary fluid systems[J]. Physical review e,1996,54(5): 5041-5052. DOI: 10.1103/PhysRevE.54.5041.
[19] ZHENG H W,SHU C,CHEW Y T. A lattice Boltzmann model for multiphase flows with large density ratio[J]. Journal of computational physics,2006,218(1): 363-371. DOI: 10.1016/j.jcp.2006.02.015.
[20] INAMURO T,OGATA T,TAJIMA S,et al. A lattice Boltzmann method for incompressible two-phase flows with large density differences[J]. Journal of computational physics,2004,198(2): 628-644. DOI: 10.1016/j.jcp. 2004.01.019.
[21] HE X Y,SHAN X W,DOOLEN G D. Discrete Boltzmann equation model for nonideal gases[J]. Physical Review e,1998,57(1): R13-R16. DOI: 10.1103/ PhysRevE.57.R13.
[22] FRISCH U,D’HUMIÈRES,HASSLACHER B,et al. Lattice gas hydrodynamics in two and three dimensions[J]. Complex Systems. 1987,1(4): 649-707.
[23] FRISCH U,HASSLACHER B,POMEAU Y. Lattice-gas automata for the Navier-Stokes equation[J]. Physical review letters,1986,56(14): 1505-1508. DOI: 10.1103/ PhysRevLett.56.1505.
[24] D'HUMIÈRES D,LALLEMAND P,FRISCH U. Lattice gas models for 3D hydrodynamics[J]. Europhysics letters,1986,2(4): 291-297. DOI: 10.1209/0295-5075/ 2/4/006.
[25] SCHULZ V P,BECKER J,WIEGMANN A,et al. Modeling of two-phase behavior in the gas diffusion medium of PEFCs via full morphology approach[J]. Journal of the electrochemical society,2007,154(4): B419-B426. DOI: 10.1149/1.2472547.
[26] SCHULZ V P,MUKHERJEE P P,BECKER J,et al. Numerical evaluation of effective gas diffusivitysaturation dependence of uncompressed and compressed gas diffusion media in PEFCs[J]. ECS transactions,2006,3(1): 1069-1075. DOI: 10.1149/1.2356226.
[27] WU W,JIANG F M. Microstructure reconstruction and characterization of PEMFC electrodes[J]. International journal of hydrogen energy,2014,39(28): 15894-15906. DOI: 10.1016/j.ijhydene.2014.03.074.
Liquid-Gas Flow in Carbon-Paper Gas Diffusion Layer of Proton Exchange Membrane Fuel Cell: A Lattice Boltzmann Simulation Study
WU Wei1,2,3,4,CHEN Wang1,2,3,4,JIANG Fang-ming1,2,3
(1. Guangzhou Institute of Energy Conversion,Chinese Academy of Sciences,Guangzhou 510640,China;2. Key Laboratory of Renewable Energy,Chinese Academy of Sciences,Guangzhou 510640,China;3. Guangdong Provincial Key Laboratory of New and Renewable Energy Research and Development,Guangzhou 510640,China;4. University of Chinese Academy of Sciences,Beijing 100049,China)
To improve the water management of proton exchange membrane fuel cell (PEMFC),the two-phase (liquid water and air) transport in the carbon-paper gas diffusion layer (GDL) of PEMFC was simulated and analyzed by using the pseudopotential multiphase lattice Boltzmann model (LBM),which mainly focused on the effects of GDL hydrophobicity on the two-phase transport. The results encompass: for a GDL of lower hydrophobicity,liquid water is easier to seep into the pore space,and thus reach a higher liquid saturation level in the GDL;while for a GDL of higher hydrophobicity,the liquid water can hardly enter the pores of smaller size,but flows along the pathways connecting the pores of relatively larger size,leading to the formation of a capillary-fingering flow.
proton exchange membrane fuel cell;pseudopotential multiphase lattice Boltzmann model;two-phase transport;carbon-paper gas diffusion layer;hydrophobicity
TK121;TM911
A
10.3969/j.issn.2095-560X.2016.05.003
2095-560X(2016)05-0351-07
吴 伟(1987-)男,博士研究生,主要从事电化学能源系统的数值模拟研究。
陈 旺(1987-)男,博士研究生,主要从事燃料电池的数值模拟研究。
蒋方明(1973-)男,博士,研究员,博士生导师,中国科学院广州能源研究所先进能源系统研究室主任,2002-2012先后工作于德国的IMM公司、葡萄牙的阿维诺(Aveiro)大学、美国的宾州州立大学,2011年4月获中国科学院“百人计划”引进海外杰出人才择优支持,主要从事电化学能量转化和存储、微尺度能量传递和转化、深层地热资源开发和利用、多尺度多物理数值模型及计算方法等研究。
2016-03-10
2016-07-22
广东省自然科学基金(2015A030308019);广州市科技计划项目(2014J4100217)
† 通信作者:蒋方明,E-mail:jiangfm@ms.giec.ac.cn
