基于测试代价敏感的不完备决策系统属性约简算法
2016-11-09谢小军徐章艳乔丽娟朱金虎
谢小军 徐章艳 乔丽娟 朱金虎
(广西多源信息挖掘与安全重点实验室 广西 桂林 541004)(广西师范大学计算机科学与信息工程学院 广西 桂林 541004)
基于测试代价敏感的不完备决策系统属性约简算法
谢小军徐章艳乔丽娟朱金虎
(广西多源信息挖掘与安全重点实验室广西 桂林 541004)(广西师范大学计算机科学与信息工程学院广西 桂林 541004)
提出不完备决策系统测试代价敏感属性约简问题,给出不一致对象集定义以及求解不一致对象集的算法。根据不一致对象的性质改进属性重要性定义,考虑测试代价因素以及不一致对象个数的改变量给出一个新的属性重要性的定义和属性重要性中权重的设置方法,并给出属性重要性的计算算法。在此基础上,给出一个时间复杂度为O(k|C|2|U|)和空间复杂度为O(|U|)的启发式属性约简算法,并通过理论分析、实例分析和实验分析说明该算法准确性和可行性。
测试代价敏感不完备决策系统属性重要性属性约简不一致对象
0 引 言
在近些年数据挖掘和机器学习的研究中,代价敏感学习得到了许多研究者的关注,也获得了重要的进展。Turney[1]提出代价敏感树算法,该算法考虑了测试代价和误分类代价。随后文献[2]中提出9种不同类型的代价:误分类代价、测试代价、计算代价、指导代价、干预代价、副作用引起的代价、获取样本的代价、不稳定性代价和人机交互的代价。这些代价在我们现实生活中也是存在的,例如在医疗系统病人需要花费金钱、时间以及其他代价来获得最终的诊断结果。因此代价问题是一项具有意义的研究。
波兰科学家Pawlak[3]在20世纪80年代提出粗糙集理论,粗糙集理论是数据挖掘中一种常见的处理模糊性和不精确性知识的数学工具。属性约简是粗糙集理论研究的主要内容之一,将代价引入属性约简问题使得其更具有现实意义和实用性[4],很多学者通过不同方面的代价敏感属性约简进行研究分析。文献[5]首先提出代价敏感粗糙集理论体系以及独立测试代价敏感决策系统,测试代价敏感属性约简目的就是以最小的测试代价获得约简结果,即最小测试代价属性约简。文献[6]中提出一个搜索树算法来解决最小测试代价属性约简问题。该算法都能得出较好的约简结果,对于较大的数据集而言搜索空间较大导致算法效率不高。文献[5]中提出一个传统启发式的最小测试代价属性约简算法。该算法时间复杂度和空间复杂度为O(|C|3|U|2)和O(|C||U|)。文献[7]中提出一种基于遗传算法的最小测试代价属性约简算法,该算法给我们提供一个很好的解决属性约简问题的思路,并且较传统的启发式算法更效率,还有很多学者提出一些改进的启发式算法[8]和快速随机的算法[9]。
在完备决策系统中测试代价敏感属性约简已经取得了一定的成功,但是在现实生活中,由于信息的缺失或者遗漏,导致决策系统不完备。因此将测试代价引入不完备决策系统具有更高的研究意义,文献[10]中提出基于测试代价敏感的不完备信息系统可变精度分类粗糙集模型,并给出了启发式的属性约简算法。本文提出一种基于容差关系的测试代价敏感不完备决策系统属性约简算法。该算法改进了传统的属性重要性的定义,在属性重要性中考虑测试代价因素得出一个新的属性重要性定义。最后通过理论分析、实例分析和实验分析说明该算法的准确性和可行性。
1 基本概念
一个决策系统可以表示为五元组:S=(U,C,D,V,f),其中U={x1,x2,…,xn}是论域(对象集); C为条件属性集; D为决策属性;f:U×(C∪D)→V是信息函数,其中F=C∪D,C∩D= ∅,V=∪Va,a∈F,Va表示属性a的值域。
定义1在决策系统S中,用“*”表示缺省值,若S中至少存在一个“*”,即至少存在a∈C,x∈U,使得f(x,a)=*,则称该信息系统为不完备决策系统。
定义2一个测试代价独立的不完备决策系统定义如下:S=(U,C,D,V,f,c),其中U,C,D,V,f与定义1中的U,C,D,V,f相同,c:表示一个测试代价函数,其中代价为一个非负数。
由于测试代价之间相互独立,测试代价函数表示为:c=[c(a1),c(a2),…,c(a|C|)]。对于∀B⊆C有条件属性集B的测试代价为:c(B)=∑c(ai),ai∈B。表1和表2给出一个简单的医疗不完备决策系统和该决策系统的测试代价向量。
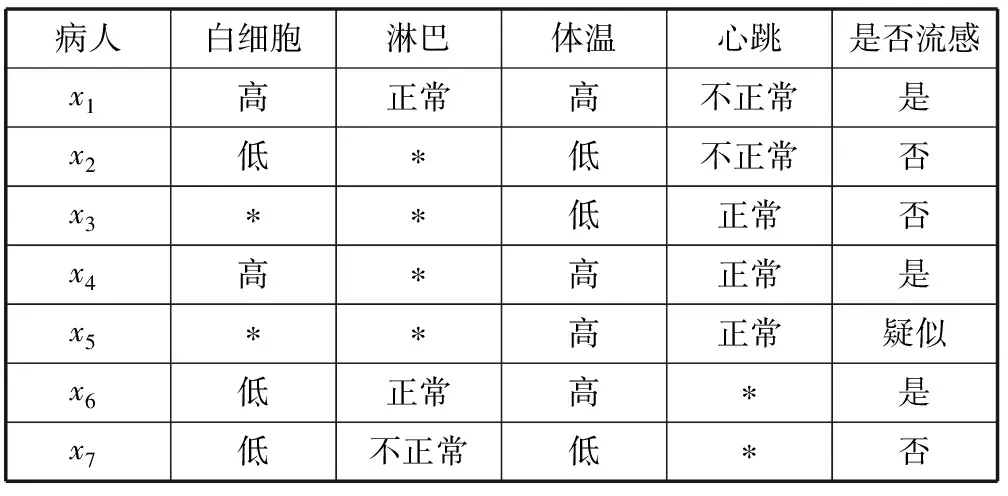
表1 一个简单的医疗不完备决策系统

表2 一个简单的测试代价向量
定义3[11]不完备决策表中S=(U,C,D,V,f),对于∀B⊆C,定义B上的容差关系T(B)如下:
T(B)={(x,y)|(x,y)∈U×U,∀b∈B,f(x,b)=f(y,b)∨f(x,b)=*∨f(y,b)=*}
TB(x)表示在B下与对象x具有容差关系的对象的集合即在条件属性集下的容差类。
定义4[12]不完备决策表S=(U,C,D,V,f)中,对于条件属性集B⊆C所产生的容差类TB(x)中,对于∀a∈B,∃y1,y2∈TB(x)有f(y1,D)≠f(y2,D)则称在条件属性集B中产生不一致对象。若B=C,则称该决策表为不一致决策表。
定义5[13]不完备决策表S=(U,C,D,V,f)中,对于B⊆C,Q⊆D,U/D={D1,D2,…,Dk}则B相对于Q的正区域定义如下:POSB(D)=∪{x|x∈U,TB(x)⊆Di},其中Di∈U/D由定义可知C相对于D的正区域可以为如下:POSC(D)=∪{x|x∈U,TC(x)⊆Di}其中Di∈U/D。
定义6[13]不完备决策表S=(U,C,D,V,f)中,对∀B⊆C,POSB(D)=POSC(D)且∀a∈B使得POSB-{a}(D)≠POSC(D)则称B是C相对于D的一个属性约简。
定义7不完备决策表S=(U,C,D,V,f)中,对于B⊆C,定义在B上产生的不一致对象集定义如下:RB={x|x∈U,|TB(x)/D|≠1},若B=∅则RB=U。
定理1不完备决策表S=(U,C,D,V,f)中,对于B⊆C在B上产生的不一致对象集与B相对于D的正区域满足:RB=U-POSB(D)。
而RB={x|x∈U,|TB(x)/D|≠1},故可有对于任意一个对象不是在POSB(D)中就是在RB即可得证RB=U-POSB(D),证毕。
性质1不完备决策表S=(U,C,D,V,f)中,对于∀B⊆C,有RB=RC和POSB(D)=POSC(D)是等价的。
由定理1可知RB=U-POSB(D),如果RB=RC那么POSB(D)=POSC(D),如果POSB(D)=POSC(D)那么RB=RC很显然两者是等价的。
性质2不完备决策表S=(U,C,D,V,f)中,对∀B⊆C,RB=RC,且∀a∈B使得RB-{a}≠RC则称B是C相对于D的一个属性约简。
性质2由性质1得到。
定理2不完备决策表S=(U,C,D,V,f)中,对∀B⊆C,a∈C-B可有RB∪{a}⊆RB。
证明:对于xi∈U,易知TB∪{a}(xi)⊆TB(xi)。
则TB∪{a}(xi)/D⊆TB(xi)/D。
可知假设|TB(xi)/D|=1那么一定有|TB∪{a}(xi)/D|=1。
而假设|TB∪{a}(xi)/D|=1那么不能确定|TB∪{a}(xi)/D|=1是否成立。
又假设|TB∪{a}(xi)/D|≠1那么一定有|TB(xi)/D|≠1。
而假设|TB(xi)/D|≠1那么不能确定|TB∪{a}(xi)/D|≠1是否成立。
由上可得xi∈U,|TB∪{a}(xi)/D|≠1的对象个数不多于|TB(xi)/D|≠1。
若x∈RB∪{a},则x∈RB。
即RB∪{a}⊆RB,即得证。由定理2易知|RB∪{a}|≤|RB|。
根据式(28)可知联立式(27)和式(29)可得累积公差与同轴度Tc的关系。依据3.3节和式(29)构建FM在Lv、Q方向的2维空间域,其2维空间域的2维空间域的位置关系如图14所示。
2 基本算法
2.1容差类
在不完备决策系统的属性约简中,求容差类的计算时间影响整个属性约简过程的效率,目前文献[14]中的求解容差类的算法较高效,该算法基于基数排序思想求容差类,时间复杂度为O(k|C||U|),其中k为条件属性中缺省对象所产生的容差类最大的个数,该算法利用文献[15]中求等价类的算法思想。但是该时间复杂度是在条件属性值为一位数据的时候才能得到此结果,基数排序的时间复杂度为O(m|U|),其中m为属性值的位数。本文提出一个新的求解容差类的算法,该算法的时间复杂度为O(k|C||U|),能更有效率更适合求属性值为多位的容差类。
算法1求测试代价独立的不完备决策系统的容差类Tai(x)
输入:S=(U,C,D,V,f,c),B⊆C,其中U={x1,x2,…,x|U|},B={a1,a2,…,a|B|}
输出:Tai(x),其中i∈[1,|B|]
Step1计算条件属性ai中f(x,ai)的最大值max和最小值min;
若存在 f(x,ai)=*max=max+1;
对于所有f(x,ai)=*f(x,ai)=max;
Step2建立一个大小为max-min的对象数组X[max-min],数组中X每一元素对应储存对象的集合(储存对象的下标来储存对象的集合),初始化X[i]←∅,i∈[0,max-min];
Step3for(j=1;j<|U|+1;j++)
X[f(xj,ai)-min]←X[f(xj,ai)-min]∪{xi}//扫描所
//有对象将每一个对象根据f(x,ai)分别储存在对象数组的每
//一个元素中(储存对象的下标来储存对象的集合);
Step4for(k=0;k ∀xj∈X[k],Tai(xj)=X[k]∪X[max-min]; Step5∀xj∈X[max-min],Tai(xj)=U。 算法1主要计算条件属性ai的容差类Tai(x)。Step1、Step2的时间复杂度为O(|U|),Step3循环|U|,故时间复杂度也为O(|U|),Step4、Step5的时间复杂度同样也是O(|U|)。故算法1时间复杂为O(|U|)。 算法2求测试代价独立的不完备决策系统的容差类TP(x) 输入:S=(U,C,D,V,f,c),B⊆P⊆C,其中U={x1,x2,…,x|U|},B={a1,a2,…,a|B|},Tai(x),TB(x) 输出:TB∪{a}(x) Step1统计所有对象f(x,a); Step2if(f(x,a′)==*) TP∪{a′}(x)=TP(x); elseif(∀x′∈Tp(x)∧f(x′,a′)==*∨f(x′,a′)==f(x,a′)) TP∪{a′}(x)=TP(x)∪{x′}; Step3输出TB∪{a}(x)。 很显然根据算法2可以求出TP(x)。该算法根据TB(x)求TB∪{a}(x)的时间复杂度为O(k|U|)其中k=max|TB(xi)|,若求TP(x)只需要循环|P-B|次时间复杂度为O(k|P-B|·|U|)而最坏的情况下空间复杂度为O(|U|)。 2.2不一致对象集 根据不一致对象集的定义,求解不一致对象集主要是要求容差类,由算法1、算法2可以快速地求解容差类,然后设计算法3求解不一致对象集以及对象集的对象个数。 算法3求测试代价独立的不完备决策系统的不一致对象集RB 输入:S=(U,C,D,V,f,c),B⊆C,其中U={x1,x2,…,x|U|},B={a1,a2,…,a|B|},TB(x) 输出:RB,|RB| Step1RB=∅;N=0;flag=0; Step2对于取任意一个对象x′∈U; Step3U=U-{x′};TB(x′)={y1,y2,…,y|TB(x′)|}; Step4if(|TB(x′)|>1) {for(i=1;i<|TB(x′)|+1;i++) if(f(yi,D)≠f(x′,D)) { RB=RB∪{x′};N++;flag=1;break;} } Step5if(flag==0) return Step2; Step6输出RB和N。 该算法主要通过求出每个对象的容差类,在容差类中是否与该对象决策值一致,不一致就把该对象并入不一致对象集中。该算法主要是计算容差类。故该算时间复杂度为O(k|C|·|U|),其中k=max|TB(xi)|。空间复杂度为O(|U|)。 定义8[5]最小测试代价属性约简定义如下:设R(S)为测试代价独立的不完备决策系统的相对约简的集合。对于∀R∈R(S),c(R)=min{c(R′)|R′∈R(S},则R就是一个最小测试代价约简。 测试代价敏感属性约简的目的就是以最小的测试代价获得约简结果,在测试代价独立的不完备决策系统中的属性约简问题可以描述如下: 问题1测试代价独立的不完备决策系统的属性约简 输入:决策系统S=(U,C,D,V,f,c),测试代价函数c* 输出:B⊆C 约束条件:RB=RC 最优化目标:minc(B) 3.1属性重要性及其计算算法 测试代价独立不完备决策系统的属性约简是一个最优或者次优约简问题,采用启发式算法解决最优或者次优约简问题相对比较理想。在建立启发式属性约简算法中,根据属性的重要性来建立启发函数可以提高算法的效率。本文同时考虑属性重要性以及测试代价因素建立一个测试代价独立不完备决策系统的属性重要性启发函数。 定义9[16]不完备决策表S=(U,C,D,V,f,c)中,属性a∈C-B(B⊆C),相对于D的属性重要性定义如下: SGF(a,B,D)=γB∪{a}-γB 其中γB=|POSB(D)|/|U| 定理3不完备决策表S=(U,C,D,V,f)中,对于B⊆C,a∈C-B,则属性重要性如下: 证明:由定义9可知属性重要性: 根据定义定理1可有: 性质3不完备决策表S=(U,C,D,V,f)中,对于B⊆C,a∈C-B,有属性重要性Sig(B,a),若Sig(B,a)=0,则POSB∪{a}(D)=POSB(D)。 证明:Sig(B,a)=0,即|RB|-|RB∪{a}|=0,|RB|=|RB∪{a}|,由定理2可知,对于∀x∈RB∪{a},则∀x∈RB,即RB∪{a}⊆RB又因为|RB|=|RB∪{a}|,可得RB∪{a}和RB一定满足RB∪{a}=RB,根据性质1,可有POSB∪{a}(D)=POSB(D),即得到性质3。 定义10测试代价独立的不完备决策系统S=(U,C,D,V,f,c)对于B⊆C,a∈C-B,则属性重要性定义如下: 说明:由定义中SIGcost为一个考虑测试代价和约简的属性重要性,SIGcost的值越大则表示属性测试代价小且该属性越重要。其中c(B)表示条件属性集B的测试代价,其中c(B∪{a})表示条件属性集B∪a的测试代价。α>0和β≥0是权重系数,且α+β=1。当β取0时表示不考虑测试代价因素,α和β的大小影响属性重要性与测试代价因素的重要性,α较大时属性重要性更重要,β较大时测试代价因素更重要。 对于定义10的属性重要性的定义,在约简过程中属性重要性和测试代价因素的权重α和β随着约简的进行不断改变。刚开始为了得到测试代价低且是重要属性的属性可以设置测试代价因素的重要性与约简的重要性等同,随着约简个数的增多对分类精度的要求变高而测试代价因素变低。本文给出一个改进后属性重要性的权值设置如下: 首先初始α和β的权值为β∅,α∅=1-β∅表示为: 随着约简个数的增多属性重要性的权值表示为: 根据该权重表达式测试代独立的不完备决策系统属性重要性可表示为: 对于SIGCOST(B,a,c)和Sig(B,a),根据算法1-算法3我们可以得出求属性重要性的计算算法。SIGCOST(B,a,c)越大且Sig(B,a)≠0表示该属性较重要,而SIGCOST(B,a,c)不管多大Sig(B,a)=0则该属性为冗余属性。下面给出改进属性重要性的计算算法。 算法4测试代价独立的不完备决策系统属性重要性的计算算法 输入:S=(U,C,D,V,f,c),B⊆C其中U={x1,x2,…,x|U|},B={a1,a2,…,a|B|},c=[c(a1),c(a2),…,c(a|c|)] 输出:sig(B,a)和SIGCOST(B,a,c(a)) Step1由算法1、2、3可以求出TB(x),RB以及|RB|; Step2对于任何一个a∈C-B由算法1、2、3可得出TB∪{a}(x),RB∪{a}以及|RB∪a|; Step3计算c(B)和c(B∪{a}); 算法4根据算法1-算法3可以依次很快速地求出结果。 算法4中Step1求TB(x)和RB的时间复杂度为O(k|C||U|),其中k=max|TB(xi)|。Step2中根据Step1的结果中求TB∪{a}(x)和RB∪{a}的时间复杂度为O(k|C||U|),其中,k=max|TB∪{a}(xi)|。Step3计算测试代价的时间复杂度为O(1)。Step4根据Step1-Step3的结果计算两个属性重要性的时间复杂度为O(1)。所以算法4主要是在求容差类和不一致对象集,故时间复杂度为O(k|C||U|),空间复杂度为O(|U|),其中k=max{|TB(xi)||B⊆C,xi∈U}。 3.2约简算法 算法4给出求解属性重要性的算法,我们可以根据算法4给出一个测试代价独立不完备决策系统的属性约简算法。 算法5测试代价独立的不完备决策系统的属性约简算法 输入:S=(U,C,D,V,f,c),其中U={x1,x2,…,x|U|},C={a1,a2,…,a|C|},c=[c(a1),c(a2),…,c(a|C|)] 输出:属性约简R Step1令R=∅; Step2对于任何一个a∈C-R根据算法求出属性重要度sig(R,a)和SIGCOST(R,a,c(a)); 计算SIGCOST(R,a′,c(a′))=maxSIGCOST(R,a,c(a)); Step3若sig(R,a′)≠0 R=R∪{a′}; Step4否则C=C-{a′};return Step2; Step5若C-R=∅; 输出R。 算法5中Step2主要计算属性重要性根据,算法4时间复杂度分析可知,该步骤时间复杂度为O(k|C||U|),其中k=max{|TB(xi)||B⊆C,xi∈U},Step3、Step4是一个循环过程,每次循环剔除一个属性,最多循环|C|次。故该算法总的时间复杂度为O(k|C|2|U|),空间复杂度为O(|U|)。 本节根据表1简单医疗不完备决策系统说明本文中的算法,其中改进的属性重要性权重设置使用本文给出的权重设置方法。将表1中属性值映射成表3所示结果。 表3 一个简单的医疗不完备系统的映射 用算法1分别求出条件属性ai的容差类Ta4(x); 对于属性a4由算法1可有max=2+1=3和最小值min=1; 建立一个数组X[max-min]=X[3-1]=X[2]; X[0]={1,2}; X[1]={3,4,5}; X[2]={6,7}; 故可得:Ta4(x1)=Ta4(x2)={1,2,6,7},Ta4(x3)=Ta4(x4)=Ta4(x5)={3,4,5},Ta4(x6)=Ta4(x7)=U 根据算法1可以依次求出Tai(x)。 再结合算法1、算法2求出TB∪{a}(x)。 |R∅|=7,根据算法3、算法4首先求出sig(∅,a)和SIGCOST(∅,a,c(a)); |Ra1|=7,|Ra2|=7,|Ra3|=4,|Ra4|=7 sig(∅,a1)=0;sig(∅,a2)=0;sig(∅,a3)=3/7;sig(∅,a4)=0 SIGCOST(∅,a1,c(a1))=0;SIGCOST(∅,a2,c(a2))=0;SIGCOST(∅,a3,c(a3))=3/7;SIGCOST(∅,a4,c(a4))=0 取最大的SIGCOST(∅,a3,c(a3))=3/7,且sig(∅,a3)≠0,则R={a3},C={a1,a2,a4} |R{a1,a3}|=4,|R{a2,a3}|=4,|R{a3,a4}|=3 sig(a3,a1)=0,sig(a3,a2)=0,sig(a3,a4)=1/7 |R{a1,a3,a4}|=3,|R{a2,a3,a4}|=3 sig({a3,a4},a1)=0;sig({a3,a4},a2)=0 均为零,C=C-{a1,a2}={a3,a4};C-R=∅;故输出属性约简R={a3,a4}。 在表1所示的一个简单医疗不完备决策系统中,我们可初步花最小的代价去检测体温和心跳,就可以快速地确诊是否患流感。这里得出的结果与现实是一致的,我们生活中去初步判断是否得了流感,首先检查体温和心跳,说明本文算法是正确的。 本节通过实验从UCI数据库中根据数据集的规模分别选取4个数据集进行实验。对本文算法(记为NEW-Algorithm)和文献[5]传统的启发式算法(记为1-Algorithm)进行实验比较。由于UCI大部分数据没有测试代价数据,本文在每组数据中增加测试代价数据,设置测试代价在[1,100]区间内,设置属性重要性权重使用本文给出的权重设置方法。实验结果记录约简个数、测试代价以及运行时间,见表4所示。 表4 两种约简算法实验结果 由表4中数据对比分析可以看出1-Algorithm算法获得的测试代价总是比NEW-Algorithm要大,并1-Algorithm算法运行时间要比NEW-Algorithm运行的时间要多,这里我们可以通过时间复杂度分析可知1-Algorithm算法时间复杂比NEW-Algorithm大得多。因此本文中的NEW-Algorithm算法改进了启发函数,比传统的启发式算法更适合测试代价敏感的属性约简问题。 在基于容差关系的不完备决策系统属性约简中,首先要计算容差类,属性约简过程大部分时间是在求容差类。设计一个更适合求容差类的算法,无论属性值为多少位都可以用该算法快速的求出,该算法改进了基于基数排序的求容差类的算法中算法时间复杂度受属性值位数的影响。根据容差类给出不完备决策系统不一致对象集的定义以及求解不一致对象集的算法。利用不一致对象集和正区域的关系,再考虑到测试代价改进属性重要性设计一个新的属性重要性的计算公式并给出属性重要性的计算方法。结合两种属性重要性的性质设计一个测试代价敏感不完备决策系统的属性约简算法。理论分析、实例分析和实验分析得出该算法的有效性和可行性。 本文只考虑了测试代价,结合误分类代价研究不完备决策系统代价敏感属性算法以及利用群智能算法解决代价敏感属性约简问题是下一步研究工作。 [1] Turney P D.Cost-sensitive classification:empirical evaluation of a hybrid genetic decision tree induction al-gorithm[J].Journal of Artificial Intelligence Research,1994,2(1):369-409. [2] Turney P.Types of cost in inductive concept learning[C]//Proceedings of the Cost-Sensitive Learning Workshop at the 17th ICML-2000 Conference,Stanford,CA,Jul 2,2000.Ottawa,CA:National Research Council of Canada,2000:15-21. [3] Pawlak Z.Rough Sets[J].International Journal of Computer and information Science,1982,11(5):341-356. [4] 林姿琼,李静宽,赵红.名词性数据的五种代价敏感属性约简算法比较[J].计算机科学与探索,2014(9):1137-1145. [5] Min Fan,He Huaping,Qian Yuhua,et al.Test-cost-sensitive attribute reduction[J].Information Sciences,2011,181(22):4928-4942. [6] Min Fan,Zhu W.Minimal cost attribute reduction through backtracking[C]//Proceedings of the 2011 Inter-national Conferences on Database Theory and Applica-tion,Bio-Science and Bio-Technology (DTA and BSBT 2011),Jeju Island,Korea,Dec8-10, 2011.Berlin,Hei-delberg:Springer-Verlag,2011:100-107. [7] Jiabin Liu,Fan Min,Shujiao Liao,et al.Test Cost Constraint Attribute Reduction Through a Genetic Approach[J].J Inf Comput Sci,2013,10(3):839-849. [8] Xu Zilong,Min Fan,Liu Jiabin,et al.Ant colony opti-mization to minimal test cost reduction[C]//Proceedings of the 2012 IEEE International Conference on Granular Computing (GrC’12),Hangzhou,China,Aug 2012.Pis-cataway,NJ,USA:IEEE,2012:585-590. [9] Li Jingkuan,Min Fan,Zhu W. Fast randomized algorithm for minimal test cost attribute reduction[C]//Proceedings of the International Conference on Reliability,Infocom Technologies and Optimization (ICRITO’13),Noida,In-dia,Jan 29-31,2013:12-17.[10] 鞠恒荣,马兴斌,杨习贝,等.不完备信息系统中测试代价敏感的可变精度分类粗糙集[J].智能系统学报,2014,9(2):219-223. [11] Kryskiewicz M.Rules in incomplete imformarion systems[J].Information Sciences,1999,113(2):271-292. [12] 刘勇,熊蓉,褚健.Hash快速属性约简算法[J].计算机学报,2009,32(8):1493-1499. [13] 王炜,徐章艳,李晓瑜.不完备决策表中基于对象矩阵属性约简算法[J].计算机科学,2012,39(4):201-204. [14] 钱文彬,杨炳儒,徐章艳,等.基于不完备决策表的容差类高效求解算法[J].小型微型计算机系统,2013,34(2):345-350. [15] 徐章艳,刘作鹏,杨炳儒,等.一个复杂度为max(O(|C||U|),O(|C|2|U/C|))的快速属性约简算法[J].计算机学报,2006,29(3):391-399. [16] 刘少辉,盛秋戬,吴斌,等.Rough集高效算法的研究[J].计算机学报,2003,26(5):524-529. ATTRIBUTE REDUCTION ALGORITHM OF INCOMPLETE DECISION SYSTEM BASED ON TEST COST SENSITIVITY Xie XiaojunXu ZhangyanQiao LijuanZhu Jinhu (Guangxi Key Lab of Multi-source Information Mining and Security,Guilin 541004,Guangxi,China)(CollegeofComputerScienceandInformationTechnology,GuangxiNormalUniversity,Guilin541004,Guangxi,China) We introduced the problem of test-cost-sensitive attribute reduction in incomplete decision system, and suggested the definition of inconsistent object set and an algorithm for computing the inconsistent object set. According to the nature of inconsistent object set we improved the definition of attribute significance. Considering the test cost factors and the varied amount of the number of inconsistent objects we presented a new definition of attribute significance and the weight setting method of it. And then we gave the calculation algorithm of attribute significance. Based on these conditions, we proposed a heuristic attribute reduction algorithm with the time complexity O(k|C|2|U|) and the space complexity O(|U|). Through theoretical analysis, example analysis and experiment analysis we explained the accuracy and feasibility of the reduction algorithm. Test-cost-sensitiveIncomplete decision systemAttribute significanceAttribute reductionInconsistent object 2015-06-12。国家自然科学基金项目(61262004,6136 3034,60963008);广西自然科学基金项目(2011GXNSFA018163);八桂学者专项基金。谢小军,硕士生,主研领域:数据挖掘,粗糙集理论及其应用。徐章艳,教授。乔丽娟,硕士生。朱金虎,硕士生。 TP18 A 10.3969/j.issn.1000-386x.2016.09.0623 属性约简算法
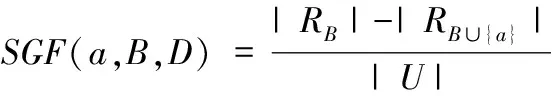

4 实例分析


5 实验分析

6 结 语
