一种使用Petri网络模型验证协议的方法

蔡俊杰



一种使用Petri网络模型验证协议的方法

蔡俊杰

随着计算机网络的高速发展，开发新型的网络协议成为热点研究课题。而新型网络协议的描述与验证又成为研究的关键。引入Petri网络模型，给出了一种协议验证的方法。通过描述Petri网络模型，该模型以其良好的直观性，为协议验证过程提供了极大的方便。并且提出了针对复杂的协议，可分解为若干个小部分，使用Petri模型，加之以有穷状态自动机和高级语言，可较完善地解决其描述和验证问题。所述的验证方法对于协议工程（protocol engineering）领域的研究，新的协议软件的产生，有着积极的推动作用。

Petri网络模型；点火；状态变迁；可达树

0 引言

当前，网络技术的发展已经进入了一个全新的时代。OSI参考模型的出现为解决异构系统的互连做出了重要贡献。但是，由于对OSI协议的开发仍常常由许多不同人员甚至是不同单位的人员进行的。因此，如何系统地开发协议软件，以确保在不同实现之间能协调地工作，仍是一个十分重要的问题。为了有效地解决这个问题，本文给出了一种使用Petri网络模型对协议进行验证的方法。

1 Petri网络模型定义

Petri网络模型是一种特殊的自动机模型。它可以用来描述通讯系统中各异步成分之间的关系。这种自动机也是一种变迁模型。它允许同时发生多个状态的变迁，因此Petri网是一种并发模型。在描述各种协议的过程中时，采用Petri网络模型是非常方便的，下面介绍Petri网的基本概念，并举例说明它在描述协议方面的应用。

包（bag）是集合的扩展，和集合相似，包也是某个域中元素的集合。但是在包里，元素可以多次出现。例如：

B1=｛a,b,c｝，B2=｛a｝，B3=｛a,a,a｝，B4=｛a,b,c,c｝，B5=｛c,c,b,b｝。B1和B2就是集合，B3~B5则不是集合。

将元素x在包B中出现的次数记为#（x,B）, 在上述例子中#（a,B1）=1，#（a,B3）=3。

当元素x为包B中的成员时，#（a,B3）=3。

当元素x为包B中成员时，#（x,B）>0。此时可写为x∈B。包B的基数定义为|B|=。在上述例子中|B5|=4。

域D是一个包中各元素的集合。Dn则是包的空间，它是元素在D中且每个元素出现不超过n次的所有包的集合。例如，当D=｛a,b,c,d｝，则D2=｛｛a,b,c,d｝,{a,a,b,b},{a,a,c,d},…｝。若B∈Dn则对于B：（1）若x∈B，则x∈D；（2）对所有的x，#（x，B）≤n。

集合D∞是域在D中所有包的集合。在每个包中元素出现的次数是没有限制的。

Petri网的定义

在上述关于包的一些基本概念之基础上，可以将Petri网定义为一个四元组C=（P，T，I，O），其中：

P=｛p1,p2, …pn｝是位置(place)的有穷集合；

T=｛t1,t2, …,tm｝是变迁的有穷集合，且T与P不相交，即T∩P=φ。

I是输入函数，是变迁T到位置包的映射，即I：T →P∞。对于每一个tk∈T，可以得出相应的I（tk）={pi,pj, …}。

O是输入函数，也是一种变迁到位置包的映射，即O：T →P∞。对于每一个对于每一个tj∈T，可以得出相应的O（tk）={pr,ps, …}。

一个Petri网的图形表示法如图1所示：

图1 Petri网的构成举例

圆圈代表位置。位置又称为节点或条件。图1 中的位置共5个。位置集合为P={p1,p2,p3,p4,p5}。短的线段代表变迁。变迁又称为事件。现在共有3个变迁，变迁集合T=｛t1,t2,t3｝。带箭头的直线或弧线指出一个变迁的输入和输出位置有哪些。

例如，在图1中：

I（t1）=｛p1｝,I（t2）=｛p2,p3,p4,p4｝，I（t3）=｛p5｝,

O（t1）={ p2,p3,p4}，O（t2）={p3,p4}。

在Petri网中最值得注意的就是位置圆圈中的黑点，称之为标记（token）。每一个位置中可以有1个或多个标记，当然也可以没有标记。Petri网所处的状态是由标记的分布决定的。在位置pi中的标记个数常用μi来表示。在图1 中μ1=2，μ2=μ3=μ4=μ5=0。这也可以用向量μ=（μ1，μ2，…μn）来表示整个Petri网的标记分布情况。可以看出，现在μ=（2，0，0，0，0）。

2 Petri网的状态变迁

一个Petri网的状态变迁取决于以下两个条件：

必须有1个或多个变迁满足变迁条件。变迁条件就是某个变迁ti的所有输入位置中都必须有标记存在，并且当输入位置有多根弧线指向这个变迁时，该输入位置也至少具有和弧线根数相等的标记数。这一条件可写为公式（1）：

对所有Pi∈I（tj）, μ（pi）≥#(Pi,I(tj)) （1）

对于图1的例子，只有t1满足变迁条件。

必须发生点火（firing）。所谓点火就是发生了一些事件（一个或多个），而这些事件所对应的变迁满足变迁条件。

发生点火后，标记要重新分布。标记移动的规则是：从点火的变迁tj的所有输入位置中均取出标记，每个位置取出的标记数等于该位置指向点火的tj的弧线数；然后再将标记送入tj的所有输出位置中去，送入每个位置的标记数等于tj指向该位置的弧线数。显然，点火前后的标记总数一般是不守恒的。上述规则可用公式表示，设点火标记前标记的分布为μ（pi），则当tj点火后，新的标记分布μ’（pi）可写为公式（2）：

μ’（pi）=μ（pi）- #（pi,I（tj））+#（pi,O（tj））（2）

可见，对于既非tj的输入位置又非tj的输出位置的其它所有位置，其中的标记数在点火前后不发生变化。

仍以图1的Petri网为例，标记的初始分布为μ=（2，0，0，0，0）。显然，只有t1满足变迁条件。当发生使t1点火的事件后，标记的分布变为μ’ =（1，1，1，1，0）。若t1再次点火，则点火后的标记分布为μ’’=（0，2，2，2，0），这时t2已具备点火条件。在t2点火后，新的标记分布变为μ’’’=（0，2，1，0，0）。至此，该Petri网已不能再发生任何点火了。至于实际的应用中，究竟是t1还是t2点火，那就要看具体的条件了。

一个Petri网中的变迁大致有以下3种类型，如图2所示：

图2 Petri网中的几种典型变迁

一种是顺序变迁，如图2（a）所示，只有当t1点火后t2才能点火。另一种是并发变迁，如图2（b）所示，t1和t2可同时（当然也可以是单独地）点火。第三种是互斥变迁，如图2（c）所示，t1和t2中只有一个能点火，一个点火后另一个就不能再点火了。至于在实际中是t1还是t2点火，那就要看具体的条件了。

3 使用Petri网对协议进行描述

下面以甲乙双方用停止等待协议通信为例，来说明如何使用Petri网对协议进行描述，如图3所示：

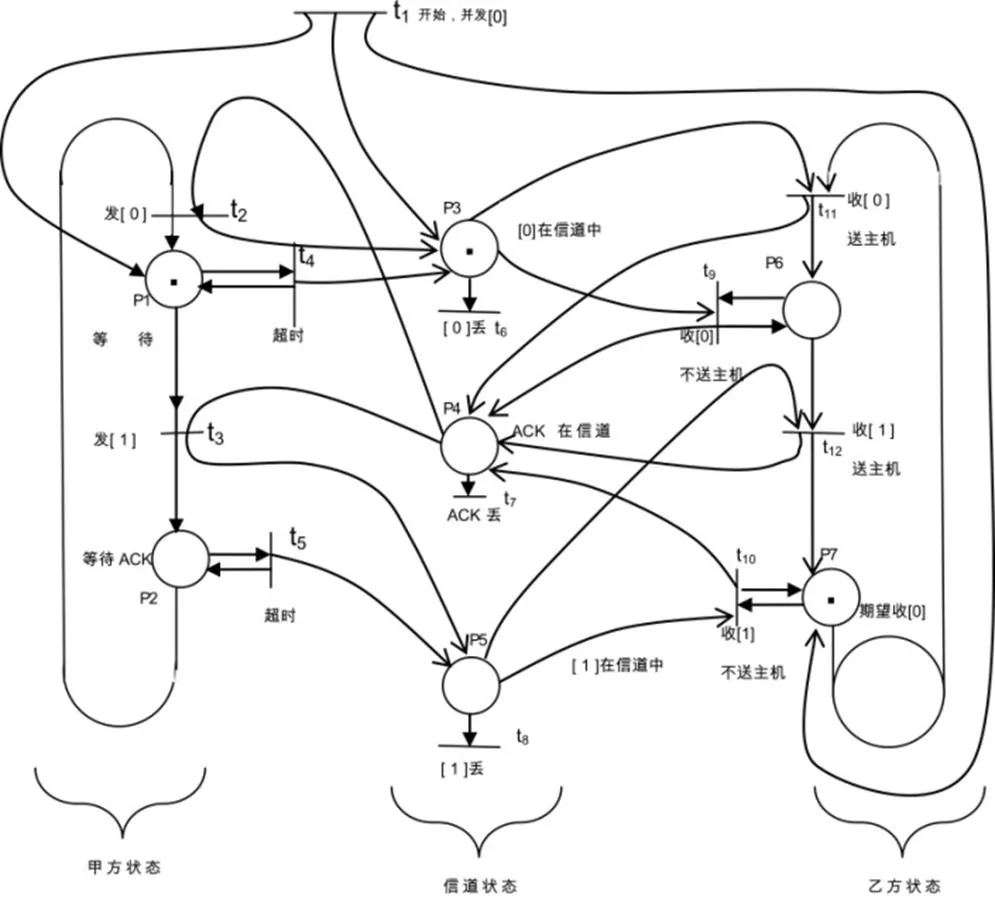
图3 半双工通信的停止等待协议的Petri网模型

在图3中，共有7个位置和12个变迁。开始时，各位置中均无标记，因此，点火只能从t1开始。t1实际上就是整个系统初始化，同时由甲方发出0号帧。t1点火后，位置p1、p3和p7中就各具有一个标记。在这种状态下，显然有3个变迁（t4、t6和t11）是满足变迁条件的。这时究竟哪个变迁点火，则要根据通信的具体情况而定。若0号帧丢失或出错，则t6点火，p3中的标记即移走（不进入任何位置），这时唯一能够点火的只有t4（超时）了。整个协议都描述得十分清楚，读者可依此自行研究每一种变迁在什么条件下方能点火，以及各种状态的转换过程。

当然Petri网同样存在着当协议较复杂时出现过多的位置和变迁，以致很难在图上将协议描述清楚。但是由于Petri有标记及点火机制，使得Petri网在验证协议的正确性方面成为很有用的工具。

Petri网模型属于状态变迁模型，用这种模型描述协议的最大优点就是直观性好，同时也便于协议的验证。

4 使用Petri网对协议进行验证

使用Petri网不但可以很直观地对协议进行描述，而且可以对协议进行验证。具体而言，利用Petri网的可达树（reachability tree）可以很方便地对协议的若干重要方面进行验证。

下面以图3中的协议为例。在一开始t1点火，标记移入位置p1,p3,p7。协议的这种状态简称为（1，3，7）。这相当于以前提到过的标记分布μ=（1,0,1,0,0,0,1）。将状态（1，3，7）作为可达树的根，如图4所示：

图4 Petri网的可达树举例

再寻找所有满足条件的变迁。找出当这些变迁点火后所达到的状态。例如，t11和t6都满足变迁条件而其余都不满足变迁条件。若t11点火，则状态变为(1，4，6，而当t6点火后，标记少了一个状态为（1，7）。这样一步一步地进行下去，直到出现一个重复的状态为止，例如在状态（1，7）下，t4点火，状态变为（1，3，7），是个曾经出现过的状态。于是可在此状态下划两道线，表示不再从该节点上继续寻找可达树。

当遍历所有可能的点火和可能出现的状态，并且所有的树叶都成为重复的状态时，Petri网的可达树即构成。

从图4得出的结果可以看出，协议中的所有可能状态从初始状态开始都是可达的，还可以看出，由于所有的树叶都是重复状态，因此，这样的协议不可能出现死锁。从可达树还可看出，本例也不会出现死循环。

还可检验出协议的动作序列都是正确的。例如，甲方从位置1到位置2再回到位置1时，t11和t12均只各点火一次，而且必须点火一次。这就保证了送交主机的帧没有遗漏，也没有重复。

大家还可注意到，若单纯从图3来考虑，则只要位置p1（或p2）中有标记，则t4（或t5）在任何时刻均可点火。例如在状态（1，3，7）时，t1点火后，使状态变为（1，32，7），这里32表示在位置3中有两个标记。若t1再次点火，则状态又变为（1，32，7）。然而根据超时定时器控制原理，刚发出魂的帧还在信道中就接连再重发这个帧是不合理的，因此这种不合理的变迁没有反映在图4的可达树中。但是当t4（或t5）点火时间不受任何限制时，位置3（或5）中的标记数将无限制地增加（因而位置4也会这样）。这样的Petri网称为无界的。与之相对应的是无穷状态自动机。实际是有用的协议都不会是这样。

从上述情况可以看出，Petri网许多特性均可以用来进行协议的验证，但是对于复杂的协议，状态数目将达到无法进行实验的程度，些时使用Petri网来解决验证问题就有困难。大家认为，此时将复杂的协议分解为若干个较小的部分，然后对这些小的部分进行验证。当协议中包含多个定时器时，要注意这些定时器设定时间的相互协调，尽量避免进程之间信息传送时间的延时。

总言之，解决协议的验证问题，应当减少人工的干预，这样才能使复杂协议的验证工作大大简化。

5 总结

网络协议的研究一直是网络技术研究的重要课题。本文所描述的Petri网络模型属于变迁模型，使用这种模型描述并验证协议的直观性好，优点明显。对于非常复杂的协议的验证，Petri网络模型与有穷状态自动机结合，对于协议的细节，辅之以高级语言来描述，这样使得协议的描述和验证均比较方便。本文所阐述的Petri网模型对协议的描述与验证方法，对于新型网络协议的研究具有积极的推动作用，具有一定的实用价值。

参考文献：

[1] 严伟,潘爱民(译)．计算机网络[M]．清华大学出版社,2012(03)．

[2] 谢希仁．计算机网络[M]．电子工业出版社,2013(06)．

[3] (美国)科姆．计算机网络与因特网[M]．清华大学出版社,2010(09)．

[4] 程莉．计算机网络[M]．科学出版社,2012(04)．

[5] 李成忠．计算机网络[M]．清华大学出版社,2010(07)．

[6] 段标, 尹晓勇．计算机网络基础[M]．电子工业出版社,2012(08)．

[7] 杨琰,廖伟志,李文敬,杨文,李杰．基于Petri网的顾及转向延误的最优路径算法[J]. 计算机工程与设计,2013,34(10): 3643-3648．

[8] 薛晨,任大勇．基于时延Petri网的双重数字签名技术研究[J].计算机与数字工程,2013,41(9):1485-1488.

[9] 傅作为乐晓波．基于Petri网的扩展工作流模型研究[J]. 计算机应用与软件,2013,30(9): 173-175．

[10] 任大勇．基于时延Petri网的移动电子支付协议模型[J].计算机与数字工程,2013,41(10):1622-1624.

Method of Protocol Validation by Using Petri Network Model

Cai Junjie

(Zhaoqing Broadcast Television University, Zhaoqing 526060, China)

With the rapid development of computer networks, the development of new network protocol has become a hot research topic. The description and validation of a new network protocol has become the key of research. This paper introduces the Petri network model, and gives the method of protocol verification. Through the description of the Petri network model, the model provides convenience for protocol verification process with good visibility. And the complex protocols can be decomposed into several small parts. By using the Petri model, it can be a better solution to the problem description and validation combining with the finite state automata and advanced language. Validation of the method presented in this paper for the protocol engineering (Protocol Engineering) research in the field and the new protocol software, has a positive role in promoting.

Petri Network model; Ignition; State Transition; Reachability Tree

1007-757X(2016)04-0078-03

TP393

A

（2015.10.15）

蔡俊杰（1968-），男，安徽人，肇庆广播电视大学，讲师。研究方向：计算机通信、计算机网络安全、信息安全等，肇庆，526060