利用汉克尔变换设计高斯光束整形衍射元件的应用研究

2016-11-09刘华

中国光学 2016年2期

关键词：傅里叶光束光斑

刘　华

(中国科学院长春光精密机械与物理研究所光电技术研发中心，吉林长春 130033)

利用汉克尔变换设计高斯光束整形衍射元件的应用研究

刘华

(中国科学院长春光精密机械与物理研究所光电技术研发中心，吉林长春 130033)

衍射光学元件由于可以实现对高斯光束的整形而被重视，其通常的设计方法为G-S算法，由于使用傅里叶变换运算量大、费时长，将快速汉克尔变换应用到这些算法中可以极大地提高运算速度，节省运算时间，为设计复杂的光束整形元件提供了高效、可行的方法。本文利用该种方法设计针对中心波长为775 nm、光束束腰口径为6 cm的激光器，成功设计了一个具有二阶相位的折衍混合光学元件。仅单独这一片元件，既可在距离其35 m处得到一半径为200 μm的圆形平顶光斑，均方根误差D<0.021。当抽样值取215时，在普通PC机上运行时间仅为20.05 s，大大节省了优化设计时间(整个优化设计过程往往需要几十次甚是上百次这种运算)。同时利用离子刻蚀技术加工了该折衍混合元件，并进行了实际测试，结果与设计值基本相符，整形效果较好。这种单片的整形元件不仅整形效果好，还有利于与激光器的集成，简化系统的调节。

衍射元件；光束整形；高斯光束；汉克尔变换

1　引　言

伴随着激光技术的发展，激光器的功率不断提升，应用也日益广泛，如激光焊接、刻蚀、扫描、打标[1-4]等。这些应用都需要满足激光光束会聚以后，光斑能量呈均匀分布，即形成平顶形状的光斑。然而实际上由激光器直接出射的激光光束，其能量分布往往呈高斯状，中心强、边缘弱，不能满足使用需求，需要利用光学方法对其进行光束整形。近年来，利用衍射光学元件进行光束匀化整形取得了极大的进展，人们已经利用位相片、全息片、二元光学器件等衍射元件获得了光强分布均匀的光斑[5-9]。用于光束整形的衍射元件其传统的设计方法有几何光学法、模拟退火法、遗传算法、G-S算法等[10-11]。其中几何光学方法计算不够精确，求得的结果往往作为G-S算法的初始值。模拟退火法、遗传算法是基于搜索极值的优化算法，鲁棒性强，要想找到最优解, 需要消耗大量的搜索时间，收敛速度很慢。G-S算法虽然收敛速度快，但是由于使用傅里叶变换，计算量大，计算周期长，很难实现快速、准确的设计和结果分析。另外在光束整形的过程中，很多情况除了需要对光束进行能量调节外，还需要在远场将能量聚焦。为了实现这两者的作用，通常做法是在衍射元件的后方再加入一片傅里叶变换透镜[12]。这样会导致光路中元件增多，调整不便，集成度不高。即使是做成单片，也基本是在平面基底上制作，导致衍射原件的位相周期比较小，为加工制作带来不便[13]。

旋转对称性质的傅里叶变换可以用快速汉克尔变换来代替[14-15]，但大部分都是用于激光光束传播过程的计算，目前还没有系统的将该算法应用于G-S整形算法中的文献报道。本文将其应用于G-S优化算法中，大大提高了计算速度，节省了计算时间。同时将衍射元件基底的另一表面制作成带有曲率的球面，形成一个折衍混合光学元件，能够同时完成光斑的匀化和聚焦功能。针对中心波长λ=775 nm的激光器，利用数学计算软件Matlab成功设计了一个具有二阶相位的折衍混合光学元件，在距离光束束腰35 cm处得到一个半径为200 μm的圆形平顶光斑，均方根误差D小于0.021。当抽样值取215时，在普通PC机上运行时间仅为20.05 s，如果使用Matlab软件中自带的傅里叶变换和逆变换函数，运算时间会超过10 min。而优化设计过程往往会需要进行几十次甚至上百次的运算，这会极大地节省优化设计时间。最后利用离子刻蚀技术将衍射位相刻制在了以平凸透镜为基底的平面上，形成了理想的高斯光束整形折衍混合元件。在实验室搭建了光斑测试系统，利用激光斑探测器接收光斑，表明设计结果理想，元件整形效果很好。同时系统只有一个光学元件，简单易调，便于集成。

2　设计方法理论分析

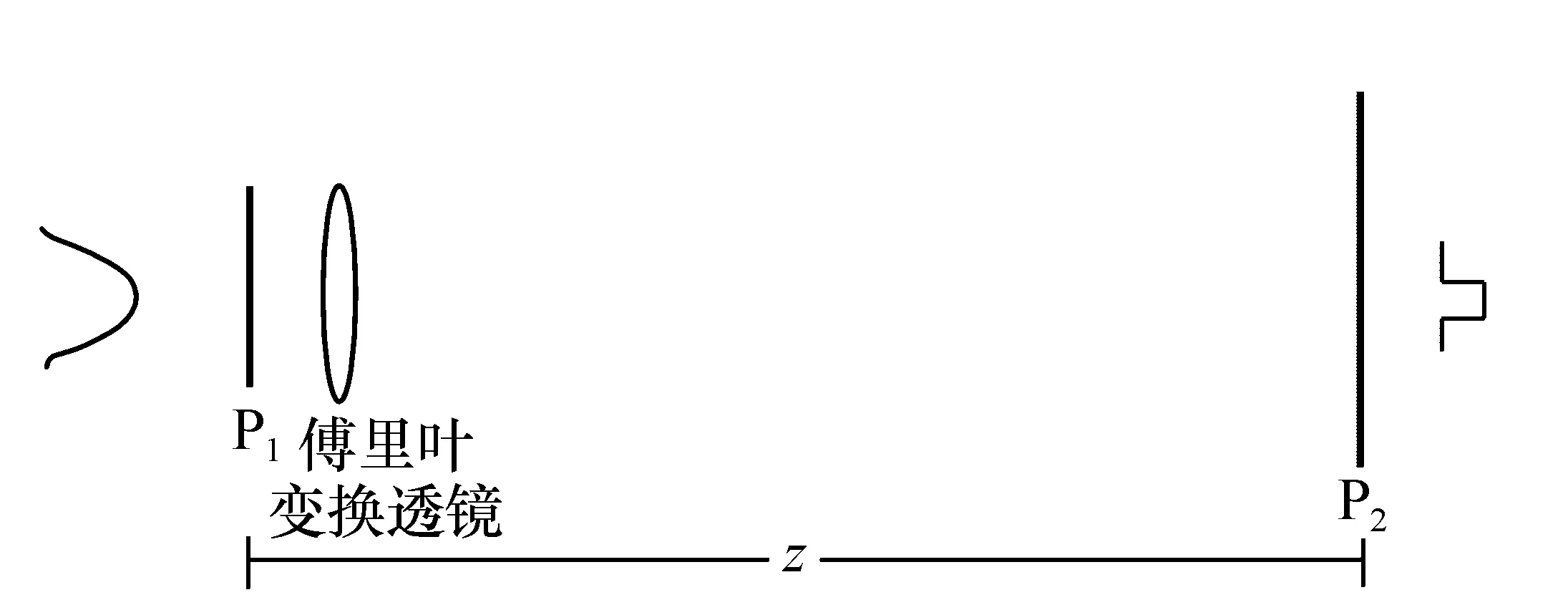
图1　光束整形的原理图 Fig.1　Schematic diagram of beam shaping

(1)

式中，r为入射光线经过P1元件表面的径向坐标，w0为高斯光束束腰半径。|f0(r)|为输入光波的实振幅，φ0(r)为输入光波的位相。衍射光学元件P1的透过率函数为

(2)

则入射光波在经过衍射光学元件P1以及透镜后的复振幅分布为

(3)

其中

对f1(r)进行傅里叶变换变换，得输出函数为

(4)

式中，p为入射光线经过P2面的径向坐标，J0为零阶贝塞尔(Besse1)函数，z为输入面和输出面的间距，C为一常数。|g1(p)|为输出光波的实振幅，φg1(p)为输出光波的位相。设计要求输出的实振幅为|g0(p)|，利用G-S迭代算法进行优化计算，便可以求得衍射光学元件的透过率函数。G-S迭代算法是一种常见的位相恢复优化计算，它的每次循环均由下列4个基本步骤组成

(5)

(6)

(7)

(8)

式中，β为实常数，一般取0<β<1。

以上计算过程是一个迭代过程，其中每次迭代都需要进行傅里叶变化和傅里叶逆变化，如果直接利用数学计算软件中的对对应函数来计算，伴随着抽样数值的增大，其计算时间以指数倍增大，甚至会造成死机。在实际计算中，如果使用快速汉克尔变换，可以大大提高计算速度，节约计算时间。根据式(5)可得

(9)

当对输入输出函数进行N次抽样时，

(10)

(11)

(12)

式中，fk(rN)≡0，k0=[2exp(a)+exp(2a)]/{[1+exp(a)]2[1-exp(-2a)]}，r0=[1+exp(a)]exp(-aN)/2。a可以通过解方程a=-ln[1-exp(-a)]/(N-1)求得。

循环过程中，利用均方根误差D作为评价函数，一旦D满足要求，循环结束，求得衍射光学元件的透过率函数。

(13)

式中，|gk(R)|i为计算中产生的输出实振幅分布的第i个抽样点值，|g0(R)|i为设计要求输出的实振幅分布的第i个抽样点值，N为抽样点数。

3　实验与结果

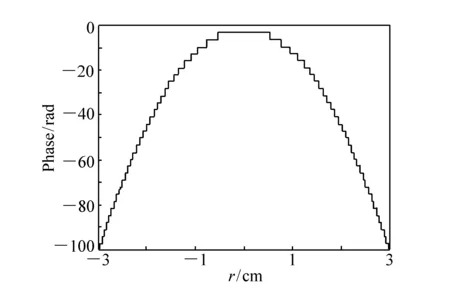
图2　衍射元件2阶位相分布图 Fig.2　Binary phase of the diffractive optical element

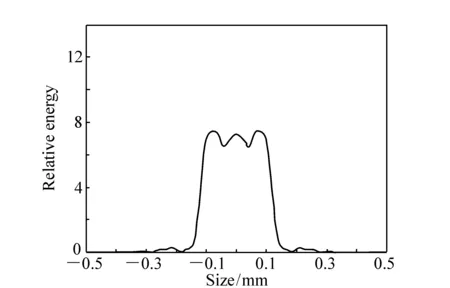
图3　接收面上能量分布的设计结果 Fig.3　Designed energy distribution on the detector plane

图4　掩膜版结构图与折衍混合元件实物 Fig.4　Configure of diffractive templet, binary refractive and diffractive optical element

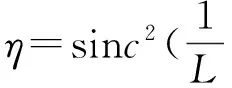
我们在实验室的光学平台上搭建了测试系统，其光路如图5所示，实物图如图6所示，能量呈高斯形状分布的775 nm激光器经过扩束镜后形成束腰口径为60 mm的准直光束。将折衍混合光学元件置于束腰处，在距离其350 mm光斑会聚的位置，利用CCD类型的光电探测器测量了整形后的光能量分布情况。由于只用一片折衍混合元件即可实现光束的整形和聚光，该系统搭建过程简单，调节方便。同时这个元件非常容易与激光器集成起来应用。

图5　测试光路图 Fig.5　Test optical system

通过使用CCD类型的光电探测器，我们首先直接测量了775 nm的激光光斑能量分布，其分布结果见图7，该图为三维能量分布图，平面坐标为光斑的径向尺寸，单位为100 μm，纵向坐标为能量值。可以明显看出中心能量最高，边缘能量低，呈高斯形状分布。然后按照实物光路结构测量了经过折衍混合光学元件整形后的光斑，其能量具体分布状况见图8(该图为三维能量分布图，平面坐标为光斑的径向尺寸，单位为100 μm，纵向坐标为能量值)，其顶部基本平坦，只是在光斑边缘处有一个小的尖峰，这主要是由于衍射元件的环带位置加工存在误差以及实验装调时各个器件相对位置存在误差等原因造成。经过计算，该光斑的尺寸为200 μm，均方根误差D=0.025，结果与设计值基本相符，整形效果很好，能够满足应用需求。说明本方法设计的整形元件不仅速度快，而且效果理想。就是说，在利用数学计算软件Matlab优化设计激光光束整形元件的过程中，将快速汉克尔变换替代其原有的傅里叶变换，可以大大提高G-S优化算法的速度，节省计算时间，同时能够获得理想的整形效果，把高斯分布的激光光束变换会聚后，得到平顶分布的光斑。

图7　高斯光束的能量分布图 Fig.7　Energy distribution of Gaussian beam

图8　整形后能量分布图 (3维立体) Fig.8　Energy distribution after beam shaping(3D)

4　结　论

本文针对中心波长λ=775 nm的激光器，成功设计了一个具有二阶相位的衍射光学元件，可以在距离光束束腰350 mm处得到一半径为200 μm的圆形平顶光斑。均方根误差D<0.021，当抽样值取215时，在普通PC机上运行时间仅为20.05 s。而使用傅里叶变换的计算时间

超过10 min。这种单次的计算时间的缩短，对于优化过程非常重要，因为整个优化设计过程往往需要反反复复进行几十次甚至上百次的计算，尤其是经验匮乏的新手，需要的计算次数就更多。同时将衍射元件与折射元件相结合，形成折衍射混合光学元件，单片就能完成对激光整形和会聚的作用，有利于及系统的集成和调节。最后通过对该衍射元件的制作和测试，表明设计结果理想，元件整形效果较好。

[1]DOPARRE.M,COLUB M A,LUDGE B,etal.. Investigation of computer-generated diffractive beam shapers for flattening of single-modal CO2laser beams[J].Appl.Opt.,2005,34(14):2487-2497.

[2]吴环宝,王肇圻,傅汝廉,等.CO2激光雕刻机的折/衍混杂f-θ镜设计[J]. 红外与激光工程,2006,35(3):351-358.

WU H B,WANG Z Q,FU R L,etal.. Design of hybrid refractive-diffractivef-θlens working on CO2laser drilling system[J].InfraredandLaserEngineering,2006,35(3):351-358.(in Chinese)

[3]HERMSDORF J,KAIERLE S. Benefits of optogalvanic effect and beam shaping for laser stabilized GMA welding[J].ChineseOptics,2014,7(1):112-117.

[4]肖龙胜,唐霞辉,秦应雄,等.2 kW射频板条CO2激光器输出光束整形特性研究[J].中国激光,2014,41(4)：1-7.

XIAO L SH,TANG X H,QIN Y X,etal.. Shaping characteristic of output beam of 2 kW radio frequency slab CO2laser[J].ChineseJ.Laser,2014,41(4)：1-7.(in Chinese)

[5]许超，张静娟.用于圆对称光束波前变换的位相型光学系统[J].物理学报,1993,42(8)：1245-1251.

XU CH,ZHANG J J. A phase only optical system for wavefront transmission of rotational symmetric beam[J].ActaPhysicSinica,1993,42(8):1245-1251.(in Chinese)

[6]包红春,邬敏贤,金国藩，等.二元光学波面变形器件的研究[J].光子学报,1994,14(9)：988-991.

BAO H CH,WU M X,JIN G F,etal.. Binary optical element for laser beam shaping[J].ActaOpticaSinica,1994,14(9):988-991.(in Chinese)

[7]刘强，李珂，杨佳，等.衍射光学元件设计中的插值迭代方法[J].计算物理,2009,26(5):731-736.

LIU Q,LI K,YANG J,etal.. Interpolation iterative arithmetic in design of diffractive optical elements[J].ChineseJ.ComputationalPhysics,2009,26(5):731-736.(in Chinese)

[8]于晓晨，胡家升，王连宝.提高激光束整形质量的新方法[J].中国激光,2012,39(1):1-6.

YU X CH,HU J SH,WANG L B. New methods for improving the quality of laser beam shaping [J].ChineseJ.Laser,2012,39(1):1-6.(in Chinese)

[9]庞辉,应朝福 ,范长江,等.用于光束整形的衍射光学元件设计的混合算法[J].光子学报,2010,39(6):977-981.

PANG H,YING CH F,FAN CH J,etal.. Design diffractive optical elements for beam shaping with hybrid algorithm[J].ActaPhoTonIcaSInica,2004,31(12):8-11.(in Chinese)

[10]陈焘,罗崇泰,王多书,等.遗传算法用于衍射光学元件的优化设计[J].光电工程,2004,31(12):8-11.

CHEN S,LUO C T,WANG D SH,etal.. Genetic algorithms used for optimization design of diffractive optical elements[J].Opto-ElectronicEngineering,2004,31(12):8-11.(in Chinese)

[11]ZHOU G Y,YUAN X C,PHILIP D,etal.. Design of diffractive phase elements for beam shaping:hybrid approach[J].J.Opt.Soc.Am.A,2001,18(4):791-799.

[12]李凤友,李红军,卢振武,等.激光直写系统焦斑整形的研究[J].光学精密工程,2001,9(1):14-18.

LI F Y,LI H J,LU ZH W,etal.. Focused spot shaping in laser writing system[J].Opt.PrecisionEng.,2001,9(1):14-18.(in Chinese)

[13]徐兵,王雪辉,陈林森,等.激光束整形为正方框形光束的DOE的设计及实验[J].激光技术,2005,29(2):169-182.

XU B,WANG X H,CHEN L S,etal.. The designation and experiment of the DOE applied to shape the laser beam to square frame shape[J].LaserTechnology,2005,29(2)：169-182.(in Chinese)

[14]ZHANG D W,YUAN X C,NGO N Q,etal.. Fast Hankel transform and its application for studying the propagation of cylindrical electromagnetic fields[J].OpticsExpress,2002,10(12) :521-525.

[15]MAGNI V,CERULLO G,SILVESTRI S D. High-accuracy fast Hankel translation for optical beam propagation[J].J.Opt.Soc.Am.A,1992,9(11)：2031-2033.

Gaussian beam shaping diffractive optical element designed by Hankel transformation

LIU Hua

(Opto-electronicsTechnologyCenter,ChangchunInstituteofOptics,FineMechanicsandPhysics,ChineseAcademyofSciences,Changchun130033,China)

，E-mail：girlliuhua@sohu.com

Because diffractive optical element can shape Gaussian beam, it is attached great importance. The conventional design methods such as G-S algorithm tend to need a large amount of calculation and a long time, while Hankel transformation can increase calculation speed and save time. We successfully designed a binary refractive and diffractive optical element applying Hankel transformation into G-S algorithm. When the diffractive optical element was placed at the waist of the laser beam with the wavelength of 775 nm and the waist diameter of 6 cm, a uniform spot could be gotten at the detector plane 35 cm behind it. Its radius was 200 μm and root-mean-square error was smaller than 0.021. The calculation time was only 20.05 s with PC, saving much time during the process of optimization, in which hundreds of calculation were needed. We fabricated the refractive and diffractive optical element by ion beam etching, and tested it in lab. The experiment results agreed well with the caculation. This kind of element not only can get good spot, but also is suitable of integration with laser.

diffractive optical element;beam shaping;Gaussian beam;Hankel transformation

2015-12-15；

2016-01-11

国家自然科学基金重点资助项目(No.61137001)

2095-1531(2016)02-0277-07

O436

10.3788/CO.20160902.0277