快速Walsh变换与多视角视频编码

于　洋，崔新宇，桑爱军，陈绵书，陈贺新，李晓妮

(吉林大学 通信工程学院，吉林 长春 130022)



快速Walsh变换与多视角视频编码

于洋，崔新宇，桑爱军*，陈绵书，陈贺新，李晓妮

(吉林大学 通信工程学院，吉林 长春 130022)

本文针对多视角视频编码提出了一种新的编码方法。在此方法中，结合四维 Walsh 操作算子，以达到压缩目的。利用4维n阶矩阵Walsh变换，对先前彩色视频流的编码加以扩展，将其应用到八个视角的视频编码中，包括视频序列分块，Walsh正变换及反变换，反分块。这种方法能够利用视频序列之间的相关性并且减少视频序列之间的冗余。本文以VC++6.0为工具，编程实现了基于快速Walsh变换的多视角视频编码，研究了不同压缩比条件下的压缩性能。通过对实验数据的分析，本文提出的方法既保证了视频质量又具有很好的快速压缩性能。实验结果表明：本文方法具有可行性及有效性，且易于在编码端快速实现，为多视角视频的进一步研究奠定了基础。

多视角视频编码；快速Walsh变换；多维矢量矩阵理论

1　引　言

随着信息科学技术的飞速发展，人们对多媒体系统的要求也随之提高，从原来的2维平面场景发展到任意视角的场景，因此多视角视频的研究成为发展趋势。

2维平面场景是由放置在固定位置的摄像机对一幅场景拍摄得到的。目前流行的3D电影则是由放置在2个不同位置的摄像机在同一时间对一幅场景拍摄得到的。多视角视频是由在同一时间放置在不同角度的一系列摄像机对同一场景拍摄得到的视频序列，能生动准确的表现场景，在各种多媒体应用中十分有效，例如身临其境的电视会议、3D电视、自由视角电视等[1-5]。然而，各个视角之间有很强的相关性，数据量非常庞大，且包含了很多冗余信息。在实际应用中，必须对多视角视频进行压缩编码，否则其存储和传输都将非常困难。如何在有限的传输带宽条件限制下，对含有巨大信息量的多视角视频进行压缩编码是亟待解决的问题。目前研究多视角视频的方法多数是基于MPEG-4或H.264结合运动补偿预测(Motion Compensated Prediction,MCP)和差值补偿预测(Disparity Compensated Prediction,DCP)的方法。他们均是单通道的视频编码，在多视角视频编码中，一个是主通道，另一个是辅通道。这种方法能处理2个视角的多视角视频，但当处理更多视角时具有一定局限性。虽然MPEG-4和H.264是非常高效的编码方法，但他们计算复杂度高，不能实时实现。一些快速算法利用宏块(MB)模式的RD特性还有编码信息的相关性来减少模式判断的复杂性。还有一些算法利用运动矢量的相关性、视差矢量的特性、运动矢量和视差矢量之间的几何关系来减少运动估计和视差估计的复杂度。以上算法虽能有效降低复杂度，但多视角视频编码的整体复杂度仍然巨大。除此之外，尽管一些算法已经考虑到量化参数变化的影响，但计算性能的稳定性和RD性能仍然有待提高[6-10]。

Walsh变换广泛应用于数字水印、图像加密、人脸识别、视频序列的压缩编码中。它既保证了重建视频质量，也使视频压缩速度得到提高，可以应用在实时视频的场合，而且是一些编码标准的主要变换方法。Walsh函数有以下特点[11-12]：

(1)Walsh函数构成简单，只由+1和-1构成。

(2)Walsh函数是完备正交的函数。

(3)Walsh函数可将乘法运算转换为实数加减法运算，减少计算复杂度，提高运算速度。

(4)随着阶数n的增大，在规定区间内+1与-1交替的次数也增多，这种特性称为序率递增特性，类似于频率递增特性。

因此，要提高多视角视频编码的效率，选择Walsh变换是一种较为有效的方法。本文以Walsh变换为基础，提出了一种针对多视角视频的编码方案。它能快速实现，并能得到较好的压缩效果和初步的压缩比。

2　离散Walsh变换及正交变换

(1)多维矢量矩阵理论

定义2-1：数域W上的M×N数据排成的M行N列数表(ai1i2)M×N称为二维矩阵，记为AM×N。W上的数表(ai1i2…in)I1×I2×…×In称为多维矩阵，记做AI1×I2×…×In。

定义2-2：如果将多维矩阵的维数划分成两组，且分别用2个矢量表示，如将AI1×I2×…×In表示为A( I1×I2×…×Im)×(J1×J2…Jn)，其中m+n=r，记做AIJ，其中I，J为矢量，I=(I1×I2×…×In)，J=(J1×J2×…×Jn)，则称多维矩阵M为按照矢量I，J划分的多维矢量矩阵，简称多维矢量矩阵。显然，一个多维矩阵可以对应多个多维矢量矩阵，而一个多维矢量矩阵只对应唯一的一个多维矩阵。

(2)多维矢量矩阵乘法及克罗内克乘积

如果两个多维矢量矩阵AIJ和BUV，其中I=(I1×I2×…×In)，J=(J1×J2×…×Jn)，U=(U1×U2×…×Up)，V=(V1×V2×…×Vq)，且J=U，则称AIJ和BUV具有可乘性。

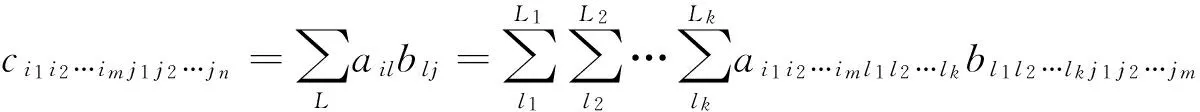
(3)克罗内克乘积

设多维矩阵AI1×I2×…×In=(ai1i2…im)I1×I2…Im，BJ1×J2×…×Jm=(gj1j2…jm)J1×J2…Jm，都是m维矩阵，则多维A与B的克罗内克乘积如下：

(1)

克罗内克乘积也成为直积或张量积。显然A⊗B仍是m阶矩阵。一般A⊗B≠B⊗A，即克罗内克乘积不满足矩阵乘法交换律[13]。

(4)一维Walsh变换

设N=2n，则离散f(x)(x=0,1,2…N-1)的Walsh变换为:

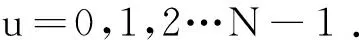
(2)

不同的序对应着不同的Walsh变换，其中最常用的是Walsh序。因此，本文中所有变换均是Walsh序的Walsh变换。

(5)二维Walsh变换

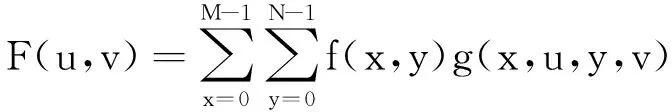
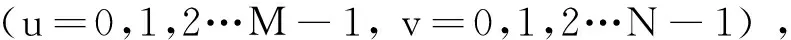
(3)

其中，变换核为:

(4)

根据Walsh变换核的可分离性，二维离散Walsh变换可分解为由两个一维离散Walsh变换所组成的形式，即:

(5)

(6)四维Walsh变换

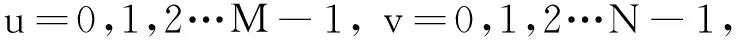
(6)

其中，变换核为:

(7)

(7)四维n阶矩阵正交变换

四维n阶矩阵：对于任意4维矩阵，若I=J=S=T,即AI×J×S×T=(aijst)n×n×n×n，则可称为四维n

阶矩阵并表示为AⅣ,n=(aijst)Ⅳ,n。显然，四维n阶矩阵就是四维n阶方阵[14-15]。

当n=2时，有

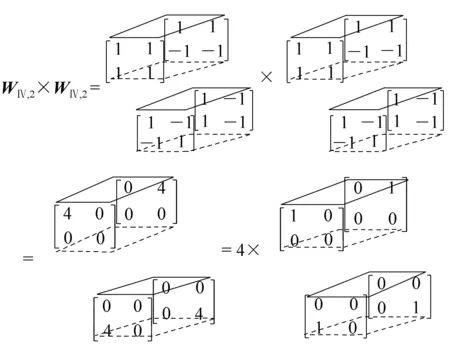
由于Walsh变换中变换矩阵简单(只含+1和-1)，占用存储空间少，产生容易，运算过程中只涉及到实数加减法运算，在需要实时处理大量数据的图像处理问题中广泛应用[16]。

3　基于快速Walsh变换的多视角编码的研究

3.1分块

本文中多视角视频编码、解码方案如图1。

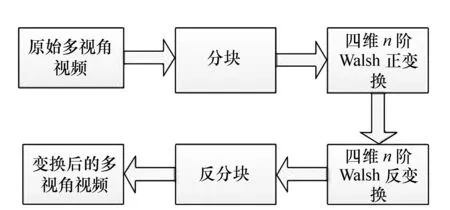
图1　多视角视频编码、解码方案 Fig.1　Multi-view video coding and decoding scheme

设K帧尺寸为I×J的视频序列，结合视频序列的特点，给出如下四维矩阵表示：

其中1≤i≤I，1≤j≤J表示视频中像素的空间位置,1≤k≤K表示视频的帧数(本文中取K=8)，1≤l≤3表示彩色视频的3个颜色算法[17]。

对于视频序列，常见的分块方式有：4×4、8×8、混合、六边形等多种分块方式，本文选取较为常用的8×8、16×16分块方式[18-19]。将实验用YUV视频中Y帧、U帧、V帧分别以8×8、16×16大小进行分块，将得到的分块按帧的顺序排列好，本实验中通过隔帧采样只取前8帧。对8个视角做相同的处理，图2给出了一个视角的分块方法。

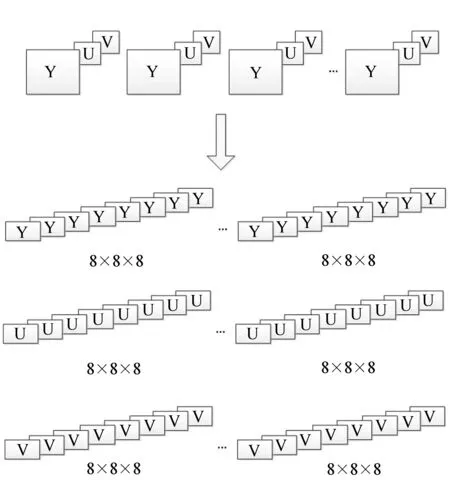
图2　一个视角的分块 Fig.2　Sub-blocking from one of eight views

3.2Walsh变换

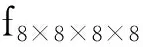
(8)

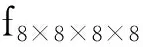
本文中所用的四维8阶Walsh操作算子WⅣ,8可由克罗内克乘积得到，即

(9)

(10)

四维2阶操作算子WⅣ,3为：

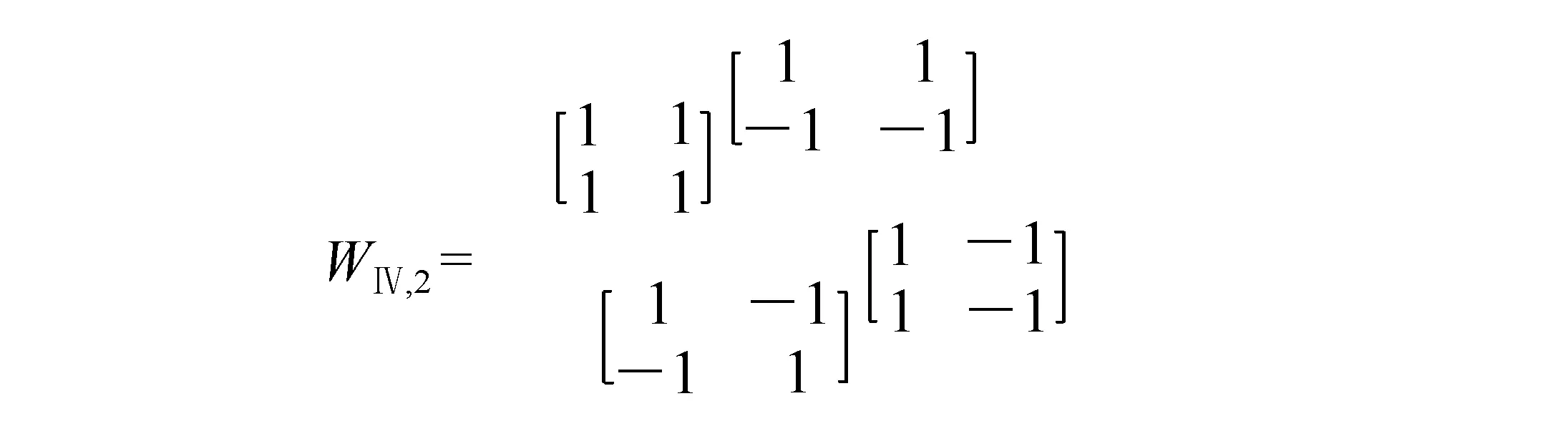
16×16分块及Walsh变换与8×8过程类似。解码过程是全部编码过程的逆过程，整个编解码过程已在第一小节给出。

4　实验结果及分析

本文中选取的是4∶2∶0的8个视角的.yuv(352×288)格式的多视角视频序列，通过隔帧采样取前8帧，分别将每个视角的数据进行8×8、16×16的分块，进行快速Walsh正变换和反变换，对变换系数矩阵取不同大小，得到不同的压缩比CR，本文中取CR=4及CR=8，最后进行反变换、反分块，得到经过处理后的多视角视频序列。在RGB格式下以变换后的峰值信噪比PSNR及压缩比CR为实验数据作为评价标准，并给出了第一、第八视角原始多视角视频与部分重建第一、第八视角多视角视频的对比。

表1为Walsh变换获得的不同分块方式对应的CR及PSNR。表2为DCT变换获得的不同分块方式对应的CR及PSNR。从表中数据可以看到，8×8的分块实验数据要优于16×16的分块实验数据。在相应分块下压缩比提高了一倍时，信噪比下降很少。在相同CR情况下，PSNR值越

大，表明压缩算法的效果越好。因此，可以针对不同的要求选取不同的分块方式及不同的压缩比，以达到理想的效果。通过与DCT变换的数据对比发现，本文所提出方法性能上与DCT变换相近。

表1　Walsh变换下不同分块方式的CR及PSNRTab.1　CR and PSNR corresponding todifferent blockings in Walsh Transform

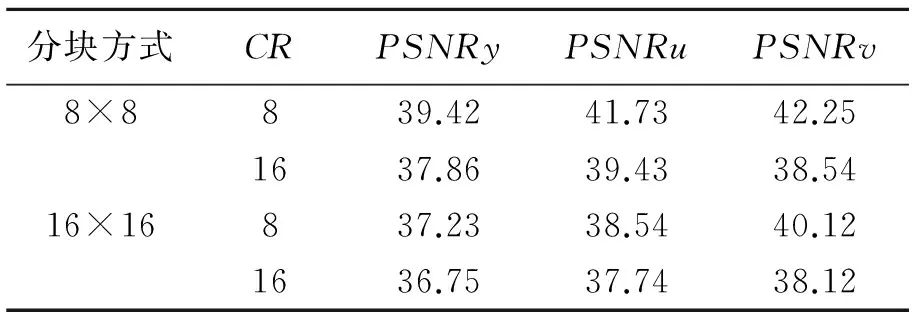
表2　DCT变换下不同分块方式的CR及PSNRTab.2　CR and PSNR corresponding todifferent blockings in DCT Transform

表3为本文方法所用时间。从时间可以看出，本文方法在保证压缩编码性能及视频质量前提下，所用时间较短，具有较快速的特点；在性能与DCT性能相近的前提下速度较快，具有一定的优越性，适合用于实时场合。

表3　本文方法所用时间(ms)Tab.3　Time consumed in this method(ms)

图3为原始多视角视频，图4为8×8分块CR=8时的重建多视角视频，图5为16×16分块CR=16时的重建多视角视频。从图3、图4及图5可以明显看出，使用本文方法获得的重建多视角视频的视频质量清晰且与原始多视角视频几乎看不出差别，满足了对视频质量的要求同时还获得了较好的CR及PSNR。

本文所用方法结合多维矢量矩阵理论，利用Walsh变换核的可分离性，可将四维Walsh变换降维处理，分解成4个一维Walsh变换，减少复杂度，提高运算效率。

图3　原始多视角视频 Fig.3　Original multi-view video

图4　8×8分块CR=8时的重建多视角视频 Fig.4　Reconstructed multi-view video of 8×8 blocking when CR is 8

图5　16×16分块CR=16时的重建多视角视频 Fig.5　Reconstructed multi-view video of 16×16 blocking when CR is 16

5　结　论

在信息技术飞速发展的今天，图像通信的数

字化已成为多媒体技术领域中的重要组成部分。多视角视频已成为当前多媒体通信研究领域中的研究热点。

本文在多维矢量矩阵理论的基础上，利用四维n阶Walsh变换对多视角视频进行编码。创新点在于对变换后的系数矩阵取不同大小，得到不同的压缩比，然后对取不同大小的系数矩阵进行反变换和反分块，得到重建多视角视频。考虑到视频序列之间的相关性，利用多维矢量矩阵模型，本文方法很好地去掉了视频序列之间的相关性，消除了冗余，达到了视频压缩的目的，且重建多视角视频与原始多视角视频几乎看不出差别，验证了其可行性。本方法在较好的压缩质量下，得到可接受的压缩比。其算法只有实数的加减法运算，易于在摄像头内硬件实现。

[1]桑爱军,穆森,王墨林,等.基于多维矢量矩阵的多视角视频编码[J].吉林大学学报(工学版),2013，43(4):1110-1115.

SANGAJ,MUS,WANGML,et al..Multi-viewvideocodingbasedonmulti-dimensionalvectormatrix[J]. J. Jilin University(EngineeringandTechnology),2013,43(4):1110-1115.(inChinese)

[2]YANGY,DAIQH,JIANGGYX,et al..Comparativeinteractivityanalysisinmulti-viewvideocodingschemes[J]. ETRI Journal,2010,32(4).

[3]JUNGJJ,HOYS.Colorcorrectionalgorithmbasedoncameracharacteristicsformulti-viewvideocoding[J]. Signal,Image and Video Processing,2014,8(5):955-966.

[4]张宝龙,李丹,王靖云,等.基于OV9712的串行器解串器视频编码方案[J].液晶与显示,2015,30(6):965-971.

ZHANGBL,LID,WANGJY,et al..ExploringtheprogramofvideocodingbasedontheOV9712SER/DES[J]. Chinese J. Liquid Crystals and Displays,2015,30(6):965-971.(inChinese)

[5]程雪岷,谈梦泽,郝群,等.自由立体显示效果测试综述[J].液晶与显示,2014,29(5):830-838.

CHENGXM,TANMZ,HAOQ,et al..Surveyonauto-stereoscopicdisplaymeasuringsystem[J]. Chinese J. Liquid Crystals and Displays,2014,29(5):830-838.(inChinese)

[6]邹虹，曾鑫，温鑫.基于两视点视频融合技术的裸眼3D显示的研究[J].液晶与显示，2014,29(5):824-829.

ZOUH,ZENGX,WENX.Glasses-free3Ddisplaybasedontwo-viewvideosynthesizetechnology[J]. Chinese J. Liquid Crystals and Displays,2014,29(5):824-829.(inChinese)

[7]王晓燕，王世刚，姜秀红，等.亮度优化立体视频视觉舒适度评价[J].中国光学，2015,8(3):394-400.

WANGXY,WANGSHG,JIANGXH,et al..Evaluationofstereovideovisualcomfortbasedonluminanceoptimization[J]. Chinese Optics,2015,8(3):394-400.(inChinese)

[8]蒋刚毅，廖义，郁梅，等.基于双目视觉特性的立体视频编码码率控制算法[J].光学 精密工程，2014,22(2):451-458.

JIANGGY,LIAOY,YUM,et al..Ratecontrolalgorithmforstereoscopicvideocodingbasedonbinocularviusualcharacteristics[J]. Opt. Precision Eng.,2014,22(2):451-458.(inChinese)

[9]王琼华,邓欢.集成成像3D拍摄与显示方法[J].液晶与显示,2014,29(2):153-158.

WANGQH,DENGH. 3Dpickupanddisplaymethodofintegralimaging[J]. Chinese J. Liquid Crystals and Displays,2014,29(2):153-158.(inChinese)

[10]王嘉辉,邓玉桃,苏剑邦,等.全高清裸眼3D显示效果的评价与测量[J].液晶与显示,2013,28(5):805-809.

WANGJH,DENGYT,SUJB,et al..Evaluationandmeasurementofdisplayeffectinfullhighresolutionautostereoscopicdisplay[J]. Chinese J. Liquid Crystals and Displays,2013,28(5):805-809.(inChinese)

[11]OUYWL,CHWK.FastalgorithmforWalshHadamardtransformonslidingwindows[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2010,32(1):165-171.

[12]PARKCS.RecursivealgorithmforslidingWalshHadamardtransform[J]. IEEE Transactions on Signal Processing,2014,62(11):2827-2836.

[13]龙清.图像压缩编码中Walsh变换与DCT变换及其比较[J].现代电子技术,2011，34(10):12-16,

LONGQ.WalshtransformandDCTtransforminimagecompressioncoding[J]. Modern Electronics Technique,2011,34(1):12-16.(inChinese)

[14]ANADA,PASCALF,FERNANDOP.OptimizedMVCpredictionstructureforinteractivemulti-viewvideostreaming[J]. IEEE Signal Processing Letters,2014,20(6):603-606.

[15]CANB,TRUONGQN.Multi-viewvideoplusdepthcodingwithdepth-basedpredictionmode[J]. IEEE Transactions on Circuit and System for Video Technology,2014,24(6):995-1005.

[16]LIP,WANGYR,LVHL,et al..Walshtransformintransientechorecognition[J]. Advanced Materials Research,2013,694:2865-2869.

[17]桑爱军，孙敏，陈绵书，等.多维矢量矩阵变换域的运动矢量估计[J].中国光学，2015,8(2):191-197.

SANGAJ,SUNM,CHENMSH,et al..Motionvectorestimationinmulti-dimensionalvectormatrixtransformdomain[J]. Chinese Optics,2015,8(2):191-197.(inChinese)

[18]LIY,CHENHX,SANGAJ,et al..Four-dimensionalmatrixWalshtransformforlosslesscompressionofcolorvideo[J]. The J. China University of Posts and Telecommunication,2010,17(3):123-128.

[19]ZHUW,ZHENGYY,CHENP,et al..Fastmacroblockencodingalgorithmbasedonrate-distortionactivityformulti-viewvideocoding[J]. Signal Processing:Image Communication,2014,29:1063-1078.

Fast Walsh transform and multi-view video coding

YU Yang, CUI Xin-yu, SANG Ai-jun*, CHEN Mian-shu, CHEN He-xin, LI Xiao-ni

(CollegeofCommunicationEngineering,JilinUniversity,Changchun130022,China)

,E-mail:sangaj@jlu.edu.cn

A fast coding method for multi-view video coding has been put forward in this paper. In this method, in order to compress the data, we combined four dimension Walsh operation. Combined with 4D n-order matrix Walsh transform, a series of coding schemes on colorful video stream proposed in previous studies was expanded and applied in eight-view video coding. The coding method includes video sub-blocking, Walsh transform and inverse transform, inverse sub-blocking, which can take advantage of the correlation of the video sequence and reduce the redundancy of the video sequence. We achieved the goal of multi-view video programming based on fast Walsh transform in VC++6.0 environment, and studied the compression performance in different compression conditions. Experiment data shows that the video quality can be guaranteed and the CR and PSNR is good. With good feasibility and effectiveness, this method is easy to achieve in the encoding side and lays a foundation for further study of multi-view video coding.

multi-view coding;fast walsh transform;multi-dimensional vector matrix theory

2015-11-11；

2016-01-12

吉林省自然科学基金资助项目 (No.20130101045JC)；吉林省科技发展计划国际科技合作资助项目(No.20130413053GH，No.20140414013GH)；国家自然科学基金资助项目 (No.61171078)；吉林省青年科学基金资助项目(No.20130522164JH)

2095-1531(2016)02-0234-07

TP919.81

A

10.3788/CO.20160902.0234

于洋(1990—),男,吉林梅河口人,硕士研究生,2012年于长春大学获得学士学位,主要从事视频图像压缩编码制方面的研究。E-mail:yy13@mails.jlu.edu.cn

桑爱军(1973—),女,山东莱州人,博士,教授,硕士研究生导师,1994年于华中理工大学获得学士学位,1997年于大连理工大学获得硕士学位,2002年于吉林大学获得博士学位,主要从事视频图像压缩编码方面的研究。E-mail:sangaj@jlu.edu.cn

Supported by Jilin Provincial Natural Science Foundation of China(No.20130101045JC), Jilin Provincial Project of International S&T Cooperation and Exchange of China(No.20130413053GH，No.20140414013GH)， National Natural Science Foundation of China(No.61171078), Jilin Provincial Natural Science Young Foundation of China(No.20130522164JH)