基于朴素贝叶斯的局部放电诊断模型
2016-11-09陈新美潘笑颜路光辉牧继清
陈新美 潘笑颜 路光辉 牧继清 姬 波
1(许昌开普检测技术有限公司 河南 许昌 461000)2(郑州大学信息工程学院 河南 郑州 450002)3(许继集团有限公司 河南 许昌 461000)
基于朴素贝叶斯的局部放电诊断模型
陈新美1潘笑颜2*路光辉3牧继清3姬波2
1(许昌开普检测技术有限公司河南 许昌 461000)2(郑州大学信息工程学院河南 郑州 450002)3(许继集团有限公司河南 许昌 461000)
针对局部放电故障诊断问题,提出一种基于朴素贝叶斯的局部放电诊断模型,并对模型中的朴素贝叶斯的应用方法进行详细研究。该模型由四部分组成:信号的接收及处理、谱图产生、特征提取和朴素贝叶斯分类。诊断流程: 首先由UHF传感器接收局部放电信号并交于信号调理单元处理;然后基于处理后的信号产生三维谱图,提取谱图的典型特征;最后采用朴素贝叶斯算法进行故障诊断。该模型已作为插件嵌入到某一电力设备生产企业的变压器监测产品中。实际测试表明该模型较好地满足了应用需求。
局部放电朴素贝叶斯诊断模型特征提取
0 引 言
局部放电[1,2]是指因为电场不均匀,高压设备绝缘的局部区域发生的发电。由于局部放电具有重复性,虽然短时间内不会影响设备的正常运行但时间长了会形成电树枝,最终导致绝缘击穿。针对局部放电信号的特征提取和模式识别问题,国内外许多学者进行了深入研究。文献[3]在全封闭气体绝缘开关设备上采集放电指纹数据,并提取了12种特征,利用复合神经网络来提高局部放电识别率;文献[4]提出利用主成分分析的方法对变压器局部放电原始特征参数进行降维,并提取出新的主成分因子,通过概率神经网络分类器对降维前和降维后的特征向量进行训练和识别;文献[5]利用超声波法提取局部放电信号,得到局放分布谱图,获得局部特征参数,通过支持向量机分类算法对典型缺陷信号进行模式识别;文献[6]使用自适应最优核(AOK)的时间-频率表示法获取局部放电的UHF信号。然后,基于时间-频率矩阵由非负矩阵分解辅助主成分分析(NMF-PCA),最后,所提取的特征被用作模糊k近邻(FkNN)分类器的输入矢量,以获得对PD识别结果。
这些研究针对局放诊断问题提出了很好的思路和方法。但是大都局限于诊断算法的研究,未涉及应用领域中多阶段整体建模问题。在实际应用中,局放诊断主要涉及四个阶段:放电信号接收及处理,谱图产生,特征提取和算法分类。它们构成了一个密切关联的整体,不可分割。因此,本文提出了一种基于朴素贝叶斯的局部放电诊断模型。该模型利用基于电磁波的UHF检测法提取局部放电信号,产生局部放电谱图,基于谱图进行特征提取,最终通过朴素贝叶斯分类算法进行模式识别,给出故障诊断结果。实测表明,作为某变压器监测产品的插件,本模型是可行的和有效的。
1 局部放电诊断模型
局部放电诊断模型如图1所示。该模型包括四个部分:信号的接收及处理、谱图产生、特征提取、朴素贝叶斯分类。流程是:从开关设备上接收局部放电信号并进行去噪处理,依次产生PRPS/PRPD/N-P/Q-P谱图,基于以上谱图进行特征提取,并采用朴素贝叶斯算法进行故障诊断。

图1 基于朴素贝叶斯的局部放电诊断模型
2 信号的接收及处理
局部放电信号经UHF传感器(天线)和高频传输电缆,送到信号调理单元,经高频滤波、放大、检波,再通过多路信号传输电缆,由高速数据采集单元进行数据采集和抗干扰处理。接收及处理流程如图2所示。

图2 信号接收和处理过程图
1) UHF天线传感器:采集局部放电的超高频信号,提取能够反映局部放电信息的特征量,如放电量、放电次数、放电相位等。天线传感器是局部放电信号接收和处理的关键设备,要求驻波比小、方向性系数高。
2) 信号调理单元:采用带通滤波及选频放大技术和包络检波技术,实现了对信号的窄带化处理,有效抑制噪声,滤除UHF传感器输出信号的超高频成分,仅保留信号的幅值和相位信息,从而降低数据采集系统的要求和减少数据量的处理。
3) 数据采集单元:数据采集单元要考虑采样率、模拟带宽、单双通道、单通道最大存储能力等。采集卡选用杭州西湖电子研究所生产设计的UHF采集模块,采样率为20M,经过检波、滤波抽点后采用TCP/IP通信协议与装置CPU进行信息交互。采集卡完成所有的采集和抗干扰处理,抽点后的数据以每周波256个点,连续采集1秒,同时4个通道的采样数据以TCP/IP传送到主CPU,每秒钟的数据流量为:256×4×50(周波)×4(通道)=0.19 MByte。
4) 信号处理:对采集到的信号进行抗干扰处理,滤除干扰信号,然后对局放信号进行放电特征量提取、放电模式识别。最后通过IEC 61850规约把处理后的放电量、放电类型等上送至综合监测单元。
3 谱图产生
采用IEC61850通信协议,将局部放电信息,包括最大放电量及平均放电量、放电次数、放电相位、放电类型上送,单位时间长度选定为1 s(50周波),生成局部放电的工频周期波形图、二维谱图(φ~q图和φ~n图)和三维谱图(φ~q~n图)。模型中图谱产生的方法如下:
1) 采用二维数组存储处理后的信号,该数组的三个列向量分别代表相位区间、幅值区间、次数;
2) 由二维数组生成三维PRPS谱图,数组的三个列向量分别对应三维图的XYZ轴;
3) 由PRPS谱图生成PRPD谱图,其方法为:定义一个三维数组存放PRPS数据,PRPS[i][j][k]。k代表放电相位,3.6度间隔,取值范围为0~99;j代表放电强度,按照dB值或者百分比处理,取值范围0~99;i代表放电周波序号,取值范围为1~50。计算方法参照式(1)。

(1)
4) 累计PRPD的j坐标值得N-P谱图,参照式(2):

(2)
5) 统计PRPD的k坐标值最大值得Q-P谱图,参照式(3):
Qmax[k]=max(j)
(3)
4 特征提取
模型中有选择性的提取了谱图的25个主要特征。其中前11个来自PRPD谱图,后14个来自N-P谱图和Q-P谱图。特征信息见表1-表3所示。

表1 基于PRPD谱图提取的特征
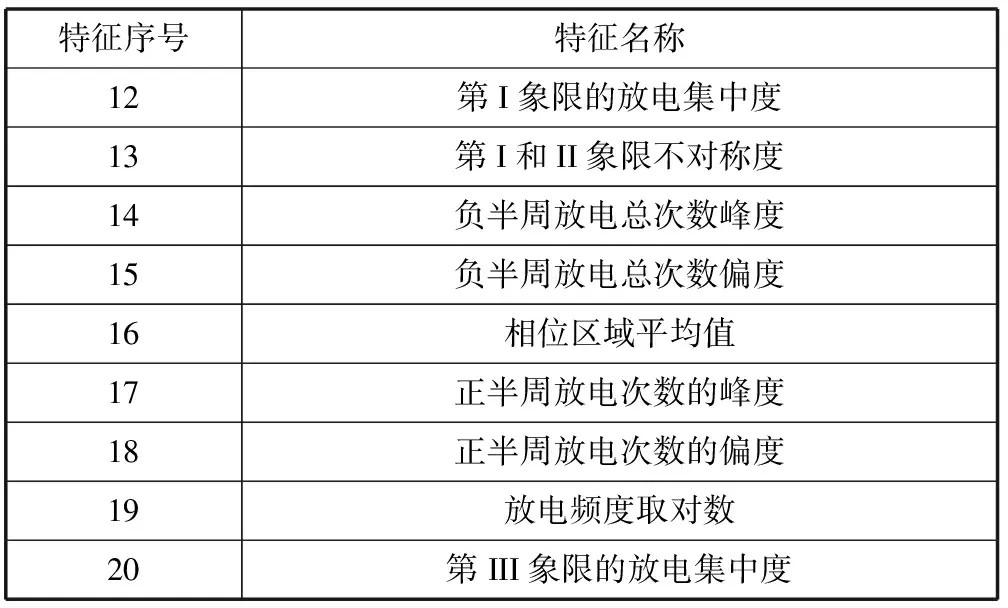
表2 基于N-P谱图提取的特征
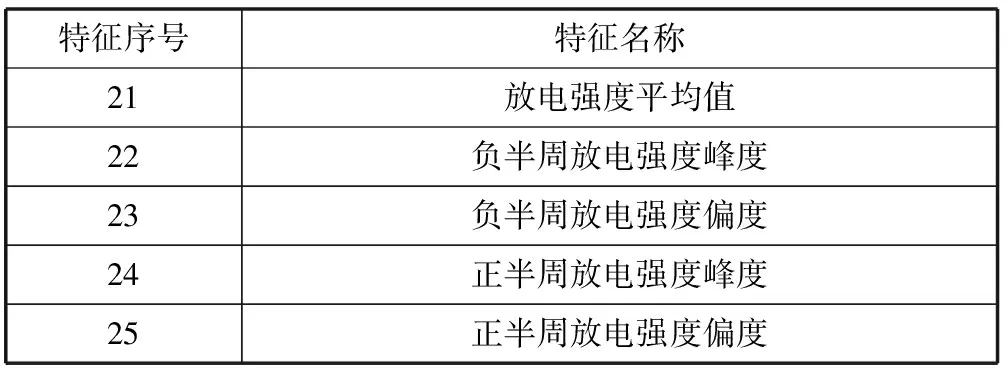
表3 基于Q-P谱图提取的特征
① 第I象限的放电集中度:0~90度相位域范围放电脉冲的比率,计算公式为式(4)。
(4)
② 第I和II象限不对称度:先计算II象限即90~180度相位域范围放电的比率,再计算不对称度,即两个象限集中度的差值。计算公式为式(5)、式(6)。
(5)
fA13=f12-f13
(6)
③ 负半周放电次数均值,参照式(7)。
(7)
④ 负半周放电次数方差,参照式(8)。
(8)
⑤ 负半周放电总次数峰度,参照式(9)。
(9)
⑥ 负半周放电总次数偏度,参照式(10)。
(10)
⑦ 相位区域平均值:每个相位区间的脉冲数与相位值的乘积累加和与脉冲总数的比值,参照式(11)。
(11)
⑧ 正半周放电次数的峰度和偏度参照负半周放电次数的峰度和偏度的计算公式。放电频度取对数,参照式(12)、式(13)。
(12)
f19=log10(Ne+1)
(13)
⑨ 第III象限的放电集中度:180~270度相位域范围放电的比率,参照式(14)。放电强度平均值,参照式(15)。
(14)
(15)
Qmax[k]为最大的放电强度。
⑩ 负半周放电强度峰度,参照式(16)-式(18)。
(16)
(17)
(18)

(19)
正半周放电强度峰度和偏度参照负半周放电强度峰度和偏度的计算公式。
5 朴素贝叶斯算法
朴素贝叶斯算法的主要思想是:将事件的先验概率和后验概率联系起来,利用先验信息和样本数据确定事件的后验概率。为了简化分类运算,朴素贝叶斯分类器在估计类条件概率时假设属性之间条件独立[7]。
给定一个实例数据集E,E={X1,…,Xn,C}。其中X1,X2,…,Xn,是属性变量,C是类型变量,其取值为{c1,c2,…,cm},Xi的取值为xi。实例Ii={x1,x2,…,xn}属于cj的概率由贝叶斯表示为:
P(cj|x1,x2,…,xn)=P(x1,x2,…,xn|cj)×P(cj)
(20)
其中类cj的先验概率是P(cj),类cj的条件概率是P(x1,x2,…,xn|cj),类cj的后验概率是P(cj|x1,x2,…,xn)。朴素贝叶斯选择后验概率最大的类cj为该实例Ii的类标签。
从训练数据估计后验概率时有一个问题:如果有一个属性的类条件概率为0,则整个类的后验概率就为0。朴素贝叶斯分类器无法分类这样的记录。为了解决这个问题,使用m估计方法来估计条件概率,即:
(21)
其中,n为类yj中的实例总数,nc是类yj的训练样例中取值xi的样例数,m是称为等价样本大小的参数,p是用户指定的参数[6]。
在本模型中考虑到放电数据的特点,分别使用两种方法估计连续属性的类条件概率:① 离散化每一个连续的属性,用相应的离散区间替换连续属性值。典型的无监督离散化方法为等宽离散化方法和等频离散化方法。② 高斯分布表示连续属性的类条件概率分布,均值μ和方差σ2是该分布的两个参数。对每个类yi,属性Xi的类条件概率为:
(22)
等宽离散化算法和等频离散化算法是两类典型的无监督离散化方法。如算法1、算法2所示。等宽离散化方法是将属性的值域划分成具有相同宽度的区间[6]。等频离散化方法是试图将相同数量的对象放进每个区间[8]。
算法1等宽离散化算法
要求:数据集S,实例数n,属性个数m,类型个数k,离散区间数L
输入:数据集S,离散区间数L
输出:离散化后的数据集合SS
方法:
1.for i in m do
2.计算第i个属性的最大值maxi和最小值mini
3.计算第i个属性的离散化宽度
widthi=(maxi-mini)/L
4.切点集
gatheri={mini+widthi,mini+
2*widthi,…,mini+(L-1)*widthi}
5.end for
6. SS = S
7.for i in n do
8.for j in m do
9.if SSij>= mini&& SSij<= mini+t*widthi
10.SSij= t
11.end for
12.end for
13.return SS
算法2等频离散化算法
要求:数据集S,实例数n,属性个数m,类型个数k,,要分的份数a
输入:数据集S
输出:离散化后的数据集合SS
方法:
1. width = n/a
2. SS = S
3. for j in m
4.按SS的第j列升序排列
5. for k in a
6.SS的第j列的(k-1)*width到k*width行都赋值为k
7.end for
8.end for
9.return SS
6 实 验
6.1实验数据集
实验数据是来自现场的63例放电数据,包括11种放电类型:分别为尖刺放电,绝缘子表面放电,均匀噪声,手机干扰,随机干扰,悬浮放电,沿面放电,噪声,噪声信号,金属颗粒和自由金属颗粒。为了保证实验的合理性,采用十次十折交叉法来求取诊断正确率的总平均值作为平均正确率。
6.2实验分析
分别使用两种估计连续属性的类条件概率的方法做实验,以便得到最好的计算连续属性的类条件概率的方法。
表4展示了等宽离散化并使用m估计的实验结果,表5展示了等频离散化并使用m估计的实验结果,表6展示了使用m估计的等宽离散化方法最优份数和等频离散化方法的最优份数。表7展示了两种计算连续属性的类条件概率的方法的结果,从表7中可以看出第一种方法比第二种方法好,并且第一种方法中等宽离散化比等频离散化的分类正确率高,高出2.5%。
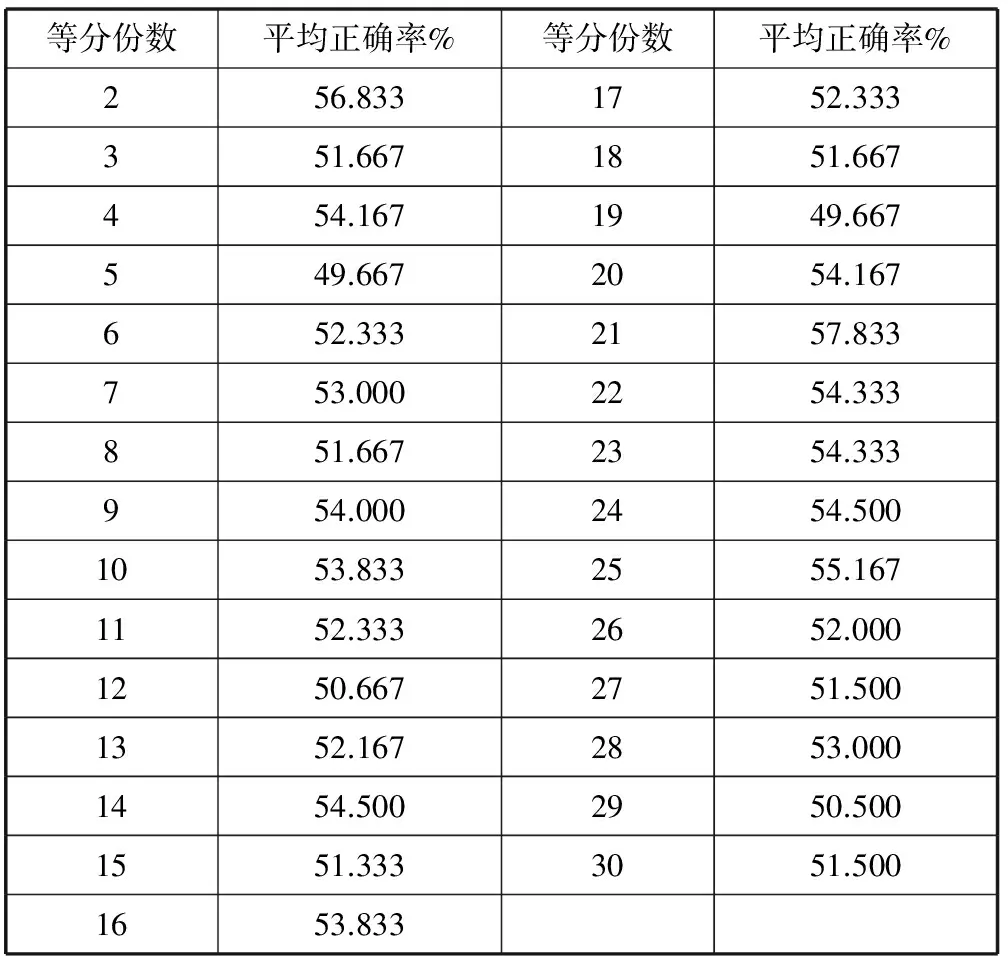
表4 等宽离散化的实验结果(m估计)

表5 等频离散化的实验结果(m估计)

表6 最优份数

表7 最高正确率对比
6.3实验结论
由于贝叶斯分类估计连续属性的类条件概率的方法对局部放电诊断有显著的影响,本文详细研究了两种估计连续属性的类条件概率的方法,进而方便模型的建立。实验表明第一种方法优于第二种方法,并且第一种方法中的等宽离散化优于等频离散化。
7 结 语
本文模型已作为重要插件嵌入到某一电力设备生产企业的变压器监测产品中。该产品的主要功能是对电力设备绝缘性能进行连续实时监测,当绝缘劣化发生局部放电时,判断电力设备是否存在缺陷,指出缺陷类型以及缺陷位置,为电力设备的维修和保养提供决策依据。本模型的任务是通过对局部放电信号的提取、分析,给出故障诊断结果。实际测试表明本模型较好地满足了应用需求。
[1] Wu Qingyan,Liu Guoqiang,Xia Zhengwu,et al.The study of Archimedean spiral antenna for partial discharge measurement[J].International Conference on Intelligent Control and InformationProcessing(ICICIP),2013,5(4):694-698.
[2] Chen S,Czaszejko T.Partial discharge test circuit as a spark-gap transmitter[J].IEEE Electrical Insulation Magazine,2011,27(3):36-44.
[3] 李培江,朱晓锦,尤婷.基于神经网络GIS局部放电模式的识别[J].中国电力,2013,46(10):60-63.
[4] 宛津莎,尚海昆.基于主成分分析和概率神经网络的变压器局部放电模式识别[J].电力自动化设备,2013,33(6):27-31.
[5] 任永恒.基于SVM算法的局部放电模式识别[J].电力科技,2014(16):153-154.
[6] Ke Wang,Jizhong Li,Shuqi Zhang,et al.Time-frequency features extraction and classification of partial discharge UHF signals[J].Electronics and Electrical Engineering(ISEEE),2014:1231-1235.
[7] 王芳,郑建柏.基于朴素贝叶斯分类的变压器故障诊断[J].电力安全技术,2013,15(9):32-34.
[8] Pangning Tan,Michael Steinbach,Vipin Kumar.数据挖掘导论[M].范明,范宏建,译.北京:人民邮电出版社,2011.
[9] 丁剑,白凤伟.一种基于相似性度量的离散化方法[J].西北师范大学学报:自然科学版,2012,48(5):43-47.
[10] 张伟.基于归一化投影直方图不变矩的图像特征提取[J].计算机工程,2011,37(1):226-228.
[11] 鲍永胜.局部放电脉冲波形特征提取及分类技术[J].中国电机工程学报,2013,33(28):168-175.
[12] 李剑,孙才新,杜林,等.局部放电图像组合特征提取方法[J].高电压技术,2004,30(6):11-13.
[13] 王国强,朱永利,刘利鹏.变压器局部放电的分步特征分析与模式识别[J].电测与仪表,2013,50(9):6-10.
[14] 禹建丽,卞帅.基于BP神经网络的变压器故障诊断模型[J].系统仿真学报,2014,26(6):1343-1349.
A PARTIAL DISCHARGE DIAGNOSIS MODEL BASED ON NAÏVE BAYES
Chen Xinmei1Pan Xiaoyan2*Lu Guanghui3Mu Jiqing3Ji Bo2
1(Xuchang Ketop Testing Technology Co.,Ltd, Xuchang 461000,Henan,China)2(SchoolofInformationEngineering,ZhengzhouUniversity,Zhengzhou450002,Henan,China)3(XUJIGROUPCorporation,Xuchang461000,Henan,China)
For the problem of partial discharge fault diagnosis, we present a Naïve Bayes-based partial discharge diagnosis model, and study in detail the application method of Naïve Bayes in the model. The model consists of four components: reception and processing of signals, spectrum maps generation, feature extraction and Naïve Bayes classification. The diagnosis flow is as follows: first the UHF sensor is used to receive partial discharging signals and transmits them to signal conditioning unit for processing. Then based on the processed signals the model generates three-dimensional spectrum map, and extracts typical features of the map. Finally it uses Naïve Bayesian algorithm to diagnose the faults. The model as an important plug-in has been embedded into the transformer monitoring products of an enterprise of power equipment production. Practical tests show that the model well satisfies the application requirements.
Partial dischargeNaïve BayesianDiagnosis modelFeature extraction
2015-05-11。国家自然科学基金项目(61170223);河南人才培养联合基金项目(U1204610);河南省科技攻关计划项目(132102210404)。陈新美,工程师,主研领域:自动化装置和智能组件检测。潘笑颜,硕士。路光辉,高工。牧继清,助理工程师。姬波,副教授。
TP3
A
10.3969/j.issn.1000-386x.2016.09.012
