B2C电子商务信息系统操作风险评估方法研究
2016-11-09谢丽霞孙伟博
谢丽霞 孙伟博
(中国民航大学计算机科学与技术学院 天津 300300)
B2C电子商务信息系统操作风险评估方法研究
谢丽霞孙伟博
(中国民航大学计算机科学与技术学院天津 300300)
针对B2C电子商务系统操作风险评估问题,提出一种基于极值理论EVT(Extreme Value Theory)的安全风险评估方法。首先,根据操作风险定义和系统风险类型构造出操作风险的量化方法。其次,以计算结果为样本数据,基于极值理论块极大值模型BMM(Block Maxima Method)对风险价值VaR(Value at Risk)方法进行改进,通过量化计算和综合分析得到系统的操作风险评估结果。实验结果表明,通过该方法获得的风险值和系统自身承受能力对比,可以解决电子商务系统的操作风险问题,并为管控电子商务操作风险提供重要依据。
电子商务操作风险风险评估极值理论风险价值
0 引 言
当今,互联网不再是单纯提供资讯的平台,它已成为社会生活工作不可或缺的工具,电子商务是在互联网之上发展出来的新一代交易模式。2013年国务院出台的《关于促进信息消费扩大内需的若干意见》明确提出,要拓宽电子商务发展空间,培育信息消费需求,加速电子商务发展。
在过去的数年间,京东、淘宝、阿里巴巴、百度、当当等互联网的先驱者为当代电子商务的发展奠定了稳定的基础,同时也刺激了B2C模式的发展。大量的B2C企业开始涌现,相比B2B、C2C等模式,B2C模式已经成为电子商务市场的主流力量。
国家经济的进步和电子商务发展的不断前进、网民网络购物意愿不断地增强,在给市场带来机会的同时也给不法分子以可趁之机,致使B2C模式自身存在的风险问题暴漏出来。其中,信用风险、市场风险和操作风险是电子商务企业面临的主要风险[1]。操作风险以它的低频高危特性可能对电子商务企业造成灾难性的后果。
操作风险在金融和保险领域已经有了较为成熟的风险管控方法,而在电子商务领域的研究和关注相对滞后。针对B2C信息系统操作风险评估问题,本文对系统操作风险的量化方法做出研究。并结合极值理论EVT和风险价值VaR方法,给定系统未来一段时间内可能出现的最大操作风险。实验表明这种方法可为中小型电子商务企业进行风险管理、风险控制和内部审计评估提供衡量依据。
1 相关工作
随着操作风险在风险管理工作中的重要性与日俱增,对操作风险的理解不能仅仅停留在“操作风险”的字面意义上,需对其背后隐藏的问题进行研究,比如自然灾害造成系统停止运转、业务流程上的操作不当和员工内部管理等问题都可能为系统带来操作风险。
英国银行协会BBA(British Bankers Assoeiation)[2]从内部程序、人员、系统等方面对操作风险进行了初步定义。Laycock等人[3]主要从顾客和内部控制两个方面着手,将一些不可控因素和顾客行为作为衡量重点,更具有合理性。Slater等人从人为因素和系统错误两个方面定义操作风险,这同Laycock等人提出的定义基本一致,令操作风险的定义更加完善。
目前,基于极值理论的操作风险度量模型主要应用在金融和保险领域。Embrechts等人[4]对金融组织发生的极端事件建模问题展开了深入研究,并运用极值理论对度量模型进行构建。Demoulin和Embrechts[5]认为考虑极值方法的非平稳性和相关性可以更好地度量操作风险。巴曙松[6]对操作风险进行细分,并分析了操作风险管理框架的建立流程。陈倩[7]应用极值理论度量操作风险,并认为只要以真实数据为向导,评估的准确性比较可信。陈宝东等人[8]在数据不足的情况下应用极值理论,有效地解决了如何计量操作风险的难题。
电子商务系统较大的操作风险通常出现在极端事件发生的情况下,如员工的非诚实操作、网络的恶意攻击、自然灾害导致的设备中断等。因此,极值理论十分适合作为管理操作风险的特定工具。
2 操作风险评估
2.1信息系统操作风险分析
根据相关工作中操作风险定义的研究和B2C模式的主要业务模块,如表1所示,可分析出系统中存在的主要操作风险。
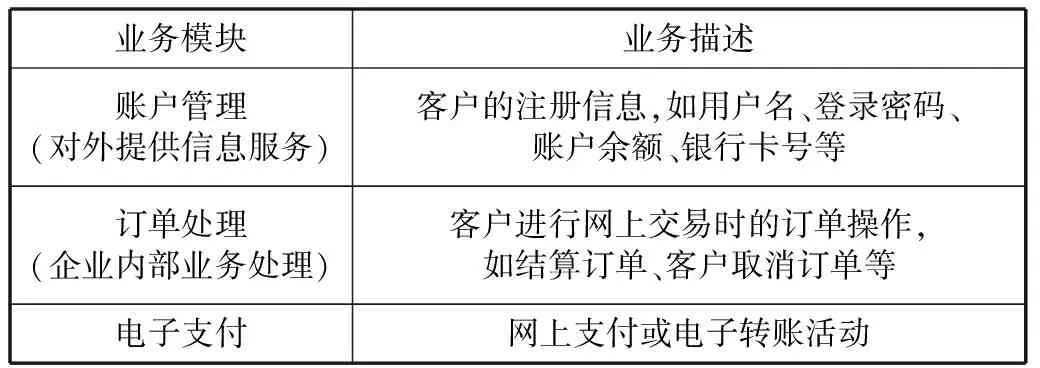
表1 B2C系统主要业务模块
系统中存在的主要操作风险如下:
(1) 系统安全性风险
电子商务是建立在Internet之上的交易模式,由于互联网的开放性系统可能会受到内部或外部的攻击。系统的瘫痪可能会导致整个电子商务系统的运行中断、客户无法进行交易、企业无法运营,将会给客户和企业带来不可预计的损失。
(2) 客户误操作风险
大部分客户的安全意识相对比较弱,他们过分地依赖信息安全产品,对自己的操作缺少警惕性。客户很可能会在不确定是否安全的环境下使用个人信息(认证信息、银行卡号、支付密码等),这将会造成个人信息的泄露。黑客可以非常轻松地访问到客户账号,进行违法操作。
(3) 内部管理风险
与传统的交易模式不同,B2C企业需要员工对业务和系统进行大批量的业务操作处理。在这期间,员工不免会出现错误操作,故意操作和非故意操作是两种常见类型。其中,非诚实员工的未授权处理是最为严重的问题,它会给企业和客户都带来灾难性的损失。
2.2操作风险量化公式
目前,国内外对信息安全风险量化方法主要分为三类:基于概率论的量化方法;基于专家知识的量化方法;模糊逻辑法;本文应用的是基于概率论和专家知识相结合的量化方法。
风险是威胁发生概率的潜在函数,预期损失概率是判断威胁发生概率的参数,预期损失程度是评估造成损失大小的衡量标准。基于这两个评估风险的重要因素,构造出的操作风险量化公式为:
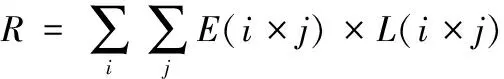
(1)
其中,R为操作风险值;i表示系统业务类别;j表示造成损失的事件类别;E为事件预期损失的概率,L为事件预期损失程度。
系统的主要业务类别i(i=1,2,3)包括账户管理、订单处理、电子支付等三个模块,如表1描述。
其中,每个业务模块的损失事件j(j=1,2,…,5)主要包括:
(1) 非人为事故(自然灾害)对系统的破坏;
(2) 电脑黑客、计算机病毒和恶意木马等侵入系统;
(3) 诚实员工的非故意操作;
(4) 非诚实员工对系统的未授权处理;
(5) 客户的不安全操作行为。
其中,预期损失概率E根据电子商务内外部环境的变化程度、各部门工作的有效性和员工职业道德操守进行评价。预期损失程度L根据专家知识和损失的补偿程度进行评价。具体步骤见4.1节操作风险计算流程。
3 基于极值理论的风险评估
3.1VaR方法
风险价值VaR[9]指在一定的置信水平下,某组织在未来特定的一段时间内可能造成的最大损失。它是一种准确的风险计算方法,已经被广泛应用于市场风险、操作风险、信用风险计算。VaR方法在风险控制、业绩评估,监管信息披露等领域已经获得了重要应用。它自身具有信息披露、资源配置、绩效评价等功能。
其数学模型如下:
假设存在连续型随机变量X为资产在特定持有期间的对数收益率, 给定(0,1)之间一个概率p,则置信水平为1-p的VaR表示如下:
VaRp=-inf{u:P(X≤u)≥p}
(2)
VaR的计算方法[10]主要包括方差-协方差方法、蒙特卡罗模拟法和历史模拟法。这三种传统的计算方法非常简单实用,其中方差-协方差方法应用最为广泛,但是计算结果的精准性存在明显的不足。接下来工作的重点是如何改进VaR的计算模型,保证计算结果的准确性。
3.2改进的VaR计算模型
传统的方差协方差法计算需要拟合正态分布,如果数据分布不符合正态分布会降低计算结果的准确性。采用基于极值理论改进的方差协方差法不仅有效的解决了上述问题,而且可以更加精确地刻画分布的尾部特征,方便观察分布情况。
研究次序统计量极值的分布特性的理论叫作极值理论EVT。它是处理与概率分布的中值相离极大的情况的理论,常用来分析罕见事件的概率情况,比如百年一遇的洪水、地震等,经常应用于风险管理和可靠性研究。
极值理论主要有两种计算模型:块极大值法BMM[11]和高限峰值法POT(Peaks over Threshold)。通常情况下,BMM模型采用广义极值GEV(Generalized Extreme Value)分布进行描述,POT模型采用广义帕累托分布GPD(Generalized Pareto Distribution)进行描述。本文采用的是BMM模型计算VaR,所以POT模型不再赘述,主要介绍BMM模型采用的广义极值分布。
假定Xi(i= 1,2,…,n)是符合独立同分布特征 (i.i.d.)的随机变量序列,它们是取自分布函数F(x)中的样本数据,将这些样本序列进行大小排序:
x1≥x2≥…≥xn
此时,则称它们为次序统计量,令Mn=max{x1,x2,…, xn}。根据Fisher-Tippett中心极限定理,若存在常数an,bn(其中an>0,bn>0)则:
(3)
该极值分布存在三种形式,分别为Frechet,Weibull,Gumbel分布,即:
Frechet:
(4)
Weibull:
(5)
Gumbel:
Λ(x)=exp(-e-x)-∞ (6) 将三种分布统一形式(GEV)进行表达,即: (7) 其中,μ,ξ∈R,σ> 0,ξ是形状参数,μ是位置参数,σ是尺度参数。当ξ> 0时,为Frechet分布。当ξ< 0时,为Weibull分布。仅当ξ=0时,为Gumbel分布。 3.3基于BMM模型的VaR计算 由于BMM模型采用GEV分布进行描述,根据广义极值分布式(7)和VaR的数学模型即可给出P值下的VaR公式: (8) 采用BMM模型处理数据需将样本按照一定的标准进行分块处理,然后在每个模块中挑选出最大值,再选取最大值作为最终的极值。处理数据的具体步骤如下: (1) 将样本值分成若干等区间; (2) 筛选区间最大值作为最终极值; (3) 对模型参数进行估计。 其中,参数估计采用极大似然估计法,根据式(7)可以得出其对数似然函数,即可对参数进行极大似然估计。 4.1操作风险计算流程 根据前文五种主要损失事件,专家可凭借经验和历史数据建立适合特定损失事件操作风险的关键控制点[12,13]来评价式(1)中的E和L矩阵: A1:恢复非人为事故(自然灾害)对系统的破坏的工作由D1部门负责; A2:防范电脑黑客、计算机病毒和木马程序等侵入系统内部的工作由D2部门负责; A3:防范诚实员工的非故意操作由D3部门负责; A4:阻止非诚实员工对系统的未授权处理由D3部门负责; A5:防范客户误操作行为所带来损失由D4部门负责。 对账户管理业务损失概率和程度做评价时的判断实例如下: (1) D1部门在出现自然灾害后,做出及时处理故障,并恢复设备,在控制此类事件中从未出现过失误,判定此类事件预期损失概率为E(1,1)=0; (2) D2部门在防范电脑黑客、计算机病毒和木马程序等侵入系统的工作上未出现过失误,判定类事件预期损失概率为E(1,2)=0; (3) D3部门负责在防范诚实员工的非故意操作工作上偶尔疏忽,则判定E(1,3)=0.3; (4) 在进行订单处理时,D3部门阻止未授权员工进入信息系统的管理方面缺乏足够经验,并有相关损失记录,则判定E(1,4)=0.7; (5) D4部门有明确的提示信息和阻止违法操作程序,能够有效地避免由于客户的错误行为导致业务中断,判定E(1,5)=0.2。 结合Kratchman等人[14]的研究对L矩阵进行评价,系统在A1、A2和A5控制点的失控对信息系统的影响较小,企业可以通过保险和免责条款对损失进行弥补工作。系统在A3和A4控制点失控可能给企业带来不可估计的损失,由于企业形象和声誉非常不容易重新塑造,所以A3和A4破坏性强,且损失程度占的比例高。最终得出5个控制点的预期损失程度比例分别为0.1,0.1,,0,5,0.2,0.1。 分别对三个业务模块的五个控制点进行评价工作,即可得到E矩阵和L矩阵,对这两个二维矩阵进行相乘计算,即得出最终R值。 4.2实验参数计算与结果分析 根据某B2C网站一年内发生的损失事件的历史记录,作为分析实验的数据源。参照BMM模型处理数据的具体步骤,拟设定分块时长为两周,每两周对系统的分块区间进行一次最大值筛选,一年内可得到24个样本极值。如图1为半年样本数据展示。 图1 一月到六月的样本数据 根据处理好的实验数据,利用极大似然估计法[15]的Matlab设计程序,对参数进行估计。结果如下: 根据参数结果可以给出P概率下的VaR值,给定0.95和0.99下的VaR值: VaR0.95=0.439VaR0.99=0.741结果表示根据过去一年的历史数据得出未来系统可能发生的最大操作风险为0.7。根据专家知识和B2C企业历史经验,该系统的操作风险处于高风险状态范围内。部门可以从5个控制点入手进行管理工作,使信息系统适应B2C模式的外部变化环境,对系统进行学习和升级。从而降低信息系统的操作风险,控制在理想状态。 通过实验结果调查,应用极值理论对系统进行风险管理可以使企业确切地估计出系统存在的最大操作风险,管理部门可以为每个员工或部门设置VaR限额来防止各部门出现过度的投机行为。如果执行严格的VaR评估管理,可以避免一些重大操作风险事件的发生。 将计算出的风险值和自身的承受能力做对比,可以解决系统的操作风险难题。为管理者的企业控制、管理操作风险提供重要依据,它是管理者做决策的有力分析工具。 操作风险对于电子商务系统的威胁正逐渐被人们所重视。由于缺乏历史数据和经验,应用于金融和保险领域的传统操作风险评估方法并不能直接嫁接于电子商务系统的操作风险评估。本文通过分析操作风险的定义和B2C模式的业务特点,构建出基于VaR方法和极值理论的评估模型。 实验结果表明,通过本文方法获得的风险值和系统自身承受能力对比,可以解决电子商务系统的操作风险问题,并为管控电子商务操作风险提供重要依据。 未来研究工作的重点是进一步完善电子商务系统的操作风险评估模型,包括改进VaR方法的其他模型(POT模型的运用)、风险量化分析表构建和设置更加有效关键内部控制点等,为中小型电子商务企业的风险管理提供更可靠的衡量依据。 [1] Rahim N A, Tafri F H. Operational risk measurement[C]//Langkawi: Statistics in Science, Business, and Engineering. 2012(7):1-4. [2] British Bankers Association. International Swaps and Derivatives Association and Robertrris Association. Operational Risk-The Next Frontier[J]. The Journal of Lending & Risk Management, 2000(3):38-44. [3] Laycock M. Analysis of Mishandling Losses and Processing Errors[M]. Operational Risk and Financial Institutions, 1998:131-145. [4] Embrechts P, Resnick I, Gennady S. Extreme value Theory as a Risk management Tool[J]. North American Actuarial Journal,1999,3(2):30-41. [5] Demoulin C, Embrechts P, NeSlehova J. Quantitative Models for Operational Risk:Extremes, Dependence and Aggregation[J]. Journal of Banking and Finance,2006, 30(10):2635-2658. [6] 巴曙松.巴塞尔新资本协议框架下的操作风险衡量与资本金约束[J].经济理论与经济管理,2003(2):17- 24. [7] 陈倩. 基于极值理论的商业银行操作风险度量研究[J]. 中国管理科学, 2012(S1):332-339. [8] 陈宝强,刘学娟.基于极值理论与蒙特卡洛模拟的商业银行操作风险度量研究[J].中国管理信息化,2014,17(6):70-73. [9] Saul I, Michael C. Encyclopedia of Operations Research and Management Science[M]. New York: Springer US, 2013. [10] 风险价值VaR的计算方法研究重庆[D].重庆大学,2013. [11] Imamverdiyev Y. An application of extreme value theory to e-government information security risk assessment [C]//Baku: Application of Information and Communication Technologies,2013(7):1-4. [12] 樊陈.基于风险管理整合框架下的电子商务系统内部控制研究[D].首都经济贸易大学,2013. [13] 黄锡远. 基于“18号指引”构建会计信息系统内部控制体系[J]. 财会月刊:会计版, 2011(9):59-61. [14] Kratchman, S H, Smith J L, Smith L M. Perpetration and Prevention of Cyber Crimes[J]. Internal Auditing, 2008,23(2):3-12. [15] 穆扬眉.极大似然估计的几种求法[J].科技信息,2011(29):30-72. ON OPERATIONAL RISK ASSESSMENT OF B2C E-COMMERCE INFORMATION SYSTEM Xie LixiaSun Weibo (School of Computer Science and Technology, Civil Aviation University of China, Tianjin 300300, China) Aiming at the problem of B2C e-commerce operational risk assessment, we proposed an EVT-based security evaluation method. First, we constructed a quantification method of operational risk according to the operational risk definition and risk types. Then, we improved the value at risk (VaR) method based on block maxima method (BMM) of EVT by adopting calculation results as the sample data. Consequently, we obtained the operational risk assessment results of e-commerce system by quantitative calculation and comprehensive analysis. Experimental results indicated that by comparing the risk values obtained with our method and the bearing capacity of system its own can solve the problem of operational risk of e-commerce system, and it can provide the important basis for controlling the operational risk of e-commerce as well. E-commerceOperational riskRisk assessmentExtreme value theory (EVT)Value at risk 2015-06-08。国家自然科学基金项目(60776807,6117 9045);国家科技重大专项(2012ZX03002002);天津市科技计划重点项目(09JCZDJC16800)。谢丽霞,副教授,主研领域:网络与信息安全。孙伟博,硕士生。 TP393.08 A 10.3969/j.issn.1000-386x.2016.09.0104 模拟实验与分析

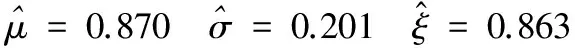
5 结 语
