直线与圆的位置关系分类与应用

安徽省蚌埠五中　杨明正

直线与圆的位置关系分类与应用

安徽省蚌埠五中杨明正

直线与圆的位置关系是高中数学的重点内容之一，我们通常将这部分内容与平面几何、直线的斜率和截距以及圆等知识结合起来进行综合考查，同时考查数形结合、函数与方程等数学思想和数学方法。为了帮助同学们更好地学习直线与圆的位置关系，本文从以下几个方面谈谈直线与圆的位置关系的分类及应用。

一、直线与圆的位置关系分类

直线与圆有三种位置关系，可以从形与数两个角度来把握。

1.几何角度。记圆心到直线的距离为d，圆的半径为r。直线与圆无公共点，则直线与圆相离，此时d＞r；直线与圆仅有一个公共点，则直线与圆相切，此时d=r；直线与圆有两个相异的公共点，则直线与圆相交，此时d＜r，直线被圆截得的线段称为圆的弦。

2.代数角度。将表示直线的方程代入圆的方程中，根据消元后所得方程的解的情况来判断，即将l的方程Ax+By+C=0（A、B不同时为0）代入圆方程（x-a）2+（y-b）2=r2中，消去x或y，不妨设消去y后得到的方程为ax2+bx+c=0，记Δ=b2-4ac。

①当Δ＞0时，直线与圆相交；

②当Δ=0时，直线与圆相切；

③当Δ＜0时，直线与圆没有公共点，即相离。

例1如果直线l：y=kx+2与圆O：x2+y2=1没有公共点，求k的取值范围。

解析 （几何法）由题意知，直线与圆相离，则圆心到直线的距离大于圆的半径，即d＞r，

直线与圆相离，则方程的判别式Δ=16k2-12（1+k2）＜0，即4k2＜12，解得。

点评本题采用了两种方法，其中代数方法（方程思想）是通性通法，适用于直线与其他曲线的位置关系以及圆与圆的位置关系问题。由于圆自身的特性，很多情况下用几何法解决此类问题更简便快捷。

练习1已知直线l：x+y-a=0和圆O：x2+y2=2，求下列情况下a的取值：

（1）直线和圆相交；

（2）直线和圆相切；

（3）直线和圆相离。

答案 （1）当-2＜a＜2时，直线l与圆O相交。

（2）当a=±2时，直线l与圆O相切。

（3）当a＞2或a＜-2时，直线l与圆O相离。

二、直线与圆的位置关系题型剖析

1.圆上的点到直线的距离问题

例2求圆C：（x-1）2+（y-1）2=4上的点到直线l：x-y-5=0的最远和最近距离。

分析首先判断直线与圆的位置关系（一般都是相离），结合圆的特性找出距离该直线最远和最近的点，再计算出最远和最近距离。

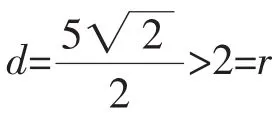
点评此类问题要结合图形和圆的性质才好解决，何时取得最大或最小值，要观察+分析+猜测+验证多措并举。

2.有关圆的切线、切点弦问题

常见的有两类：（1）圆x2+y2=r2上一点P（x0，y0）处的切线方程为l：x0x+y0y=r2；若P点在圆外，则l为过P点的与圆相切的两条切线的切点弦所在的直线。（2）圆（x-a）2+（y-b）2=r2上一点P（x0，y0）处的切线方程为l：（x-a）（x0-a）+（y-b）（y0-b）=r2；若P点在圆外，则l为过P点的与圆相切的两条切线的切点弦所在的直线。

例3求过点P（3，4）的圆（x-1）2+（y+1）2=4的切线方程。

分析过圆外一点作圆的切线，切线必有两条，可以先把直线设出来，再根据条件列方程求出待定参量。

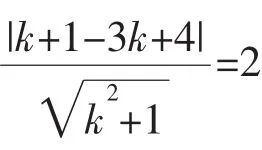
点评对于圆外一点P（x0，y0），若求出的斜率只有唯一的值，则另外一条切线方程必为：x= x0；若求出的斜率有两个值，则直接代入切线方程的点斜式，最后将切线方程化为一般式。

例4过点P（3，4）向圆C：x2+y2=1作切线，切点分别为E、F，求过点E、F的直线方程。

解过点E、F的直线方程即切点弦所在的直线方程，应该是3x+4y=1。

点评此类问题，按照常规思路应该把两条切线方程求出来，再用方程思想求出切点，最后用两点式写出切点弦所在的直线方程，比较烦琐。利用上述方法更显简洁。

3.有关圆的弦长问题

直线与圆相交通常会涉及弦长问题，求弦长的方法一般有两种：由直线方程和圆的方程联立解得交点坐标，然后利用两点间距离公式求得，这种方法计算量较大；利用由半弦、半径和圆心到直线的垂线构造直角三角形去解决，这种方法比较简单。

例5设直线ax-y+3=0与圆（x-1）2+（y-2）2=4相交于A、B两点，且弦AB的长为，求a值。

解半弦、半径和圆心到直线的垂线可构造成直角三角形，因为半弦长为，半径长为2，所以圆心（1，2）到直线的距离等于1，即有，解得a=0。

练习2直线x+2y=0被圆x2+y2-6x-2y-15=0截得的弦长为______ _。

4.有关直线与圆的位置关系综合应用问题

对于有关直线与圆的一些稍难的问题，我们可以结合圆的性质，抓住问题的本质，充分利用数形结合、转化归纳及分类讨论等思想方法加以解决，往往可以收到事半功倍的效果。

例6已知圆C：（x-1）2+（y-2）2=25，动直线l：（2m+1）x+（m+1）y-7m-4=0（m∈R）。求证：无论实数m取何值，动直线l与圆C总相交于两点。

分析通常情况下，我们在研究直线与圆的位置关系时，可联立直线与圆的方程构成方程组，消元整理成关于x或y的一元二次方程，借助判别式判断方程解的情况，确定直线与圆的位置关系，但这种方法运算量很大。其实我们还可以将圆心到直线的距离与半径进行比较来确定。而本题中的距离的最值求解相当复杂，为此抓住动直线过定点这一几何性质，通过比较定点到圆心的距离与圆的半径（点与圆的位置关系）来解决问题。

证明 （2m+1）x+（m+1）y-7m-4=0可化为（2x+y-7）m+x+y-4=0。

练习3已知圆C：x2+y2-6x-8y+21=0和直线kx-y-4k+3=0。求当k取什么值时，直线被圆截得的弦最短，并求这条最短弦的长。