基于稀疏分布特征的井下微地震信号识别与提取方法

李稳, 刘伊克, 刘保金

1 中国科学院地质与地球物理研究所，中科院页岩气与地质工程重点实验室， 北京　100029 2 中国科学院大学， 北京　100049 3 中国地震局地球物理勘探中心， 郑州　450002



基于稀疏分布特征的井下微地震信号识别与提取方法

李稳1,2,3, 刘伊克1*, 刘保金1，3

1 中国科学院地质与地球物理研究所，中科院页岩气与地质工程重点实验室， 北京100029 2 中国科学院大学， 北京100049 3 中国地震局地球物理勘探中心， 郑州450002

井下微震监测获得的地震记录往往包含大量的噪声，记录信噪比很低.有效地震信号的识别与提取是进行后续地震定位等工作之前需要优先解决的问题.经过研究发现，井下水压裂微地震信号具有稀疏分布的特征，而井下环境噪声则具有更多的Gaussian分布特征.为此，本文提出将图像处理领域适宜于稀疏分布信号降噪处理的稀疏码收缩方法应用于井下微震监测数据处理.为解决需要利用与待处理数据中有效信号成分具有相似分布特征的无噪信号序列估算正交基以及计算效率等问题，将原方法与小波变换理论相结合.即通过优选小波基函数作为正交基进行小波变换将信号分解为不同级的小波系数，利用稀疏码收缩方法中对稀疏编码施加的非线性收缩方式作为阈值准则对小波系数进行改造.通过多方面的数值实验证明了该方法在处理地震子波及井下微地震信号方面准确可靠.含噪记录经过处理后有效地震信号的到时、波形、时频谱特征等均能得到良好的识别和恢复.并且该方法具有很强的抗噪能力，当信噪比低至-20～-30 db时，仍然能够发挥作用.在处理大量实际井下微震监测数据的过程中，面对多种复杂情况，本方法展现出了计算效率高、计算结果可靠、应用简单等优势，证明了其本身具有实际应用价值，值得进一步的研究和推广.

微震监测; 水力压裂; 稀疏分布特征; 信号识别与提取; 小波变换; 去噪

In the processing mass downhole microseismic monitoring data, upon a careful study we found that the signals of downhole microseismic events triggered by hydraulic fracturing are characterized by sparse distribution. The background noise has a more significant Gaussian distribution. The relationship between signals and noise is additive blending. Therefore, this study suggests to apply the sparse code shrinkage method, which is present in image processing field, to the processing of downhole microseismic monitoring data. To solve the issues of computational efficiency and needing noise-free training data which have similar statistical properties with the signal component of the data to be processed, we combine the original method with wavelet transformation. That is, we select suitable wavelet bases to take the place of orthogonal bases, and utilize the nonlinear shrinkage process mode of the sparse code shrinkage method as the threshold rule of the wavelet threshold de-noising method.

Through many times of numeric simulation tests, it is confirmed that the method presented in this paper is accurate and reliable in processing of seismic wavelet and downhole microseismic signals. The information of arrival time, waveforms, and time-frequency spectra of the effective signal can be well recovered from the noised seismic records. In addition, this method possesses strong anti-noise ability. When the SNR is as low as -20～-30 decibels, the method can still work well. In the process of dealing with the actual data, the method has shown its advantages such as high computation efficiency, accurate calculation, and simplicity of usage. All of these verify the method has a high value of practical application.

The downhole microseismic signal recognizing and extracting method based on sparse distribution features has theoretical rationality in processing the hydraulic fracturing microseismic signals, which is a kind of signals with a sparse distribution feature and time-dependent frequency feature. Various numeric simulations and tests on real data processing confirmed this method is applicable. It deserves further research and can be used widely.

1　引言

在对低渗油气田和非常规油气田开采的过程中，为了提高采收率、提高出油量常采用“水力压裂法”这一有力的增产措施.进行水力压裂时大量的高黏度流体被高压注入储层，使得岩层的受力情况剧烈改变、发生破裂，产生大量的微地震事件.通过记录、处理、分析这些微震事件产生的地震波，可以反演出各个微震事件的发生位置，进而拟合出裂缝的空间展布，对地下水力压裂工程进行监测和生产指导.这种井下微震监测技术得到了国外多家石油服务公司(如Schlumberger、Microseismic、南非ISS公司)的大力研究与推广.我国自21世纪初将该技术引入国内以来，在大庆、辽河、长庆等多个油田展开了应用，对油气开采起到了指导作用(刘振武等, 2013).

由于工作环境等多方面的原因，在生产过程中得到的井下微震监测记录往往包含大量的噪声，数据信噪比很低.有效地震信号的识别与提取是进行井下微震监测的基础和前提.在进行大量井下微震监测数据处理的过程中，经过研究发现与普遍具有Gaussian(高斯)分布特征的井下环境噪声相比，井下微地震信号具有更多的Super-Gaussian(超高斯)分布特征，服从稀疏分布，并且信号与噪声的关系为加性混合.对于具有此类分布特征的信号，Hyvärinen(1999)提出了根据最大似然估计向信号的稀疏编码(Sparse Coding)施加一种非线性收缩的稀疏码收缩(Sparse Code Shrinkage)去噪方法，并将其应用于图像处理领域取得了良好的效果.

本文进行了将这种适宜于处理具有稀疏分布特征信号的方法应用于井下微震监测数据处理的研究.在研究过程中我们发现，应用稀疏码收缩方法处理井下微地震数据需要解决一些关键问题，主要在于：原方法需要根据与待处理数据中有效信号成分具有相似分布特征的无噪信号序列估算正交基；并且在计算效率方面缺少类似于FFT、Mallat的经典快速算法.为此，本研究将其与小波变换理论相结合.通过优化选择合适的小波基函数解决正交基估算的问题，并利用小波理论中成熟的Mallat快速算法解决计算效率问题.将稀疏码收缩方法中对稀疏编码施加非线性收缩的处理方式作为阈值准则对含噪信号经过小波变换后得到的小波系数进行处理，是本文方法的核心内容.对于具有稀疏分布特征的井下水压裂微地震信号来说，大量的数值实验和实际数据处理结果均表明上述方法具有更好的针对性，对噪声的抑制和对有效信号的识别和保护均更为有力.

2　原理和方法

2.1井下水压裂微地震信号的稀疏分布特征

信号稀疏性的概念来自信息论，可采用信息熵(简称“熵”)来量化.熵值越小，说明信号的均匀性越差，分布越稀疏.而稀疏分布通常是指信号具有Super-Gaussian分布(指随机过程的四阶累积量恒大于零并且关于其均值对称分布)特征(蒋瑜等, 2005)，表现为概率密度函数在零点处存在一个尖峰并拖有重尾.Hyvarinen指出(Hyvärinen et al., 1999)，若某信号具有稀疏分布特征，其概率密度函数应符合以下模式：

(1)

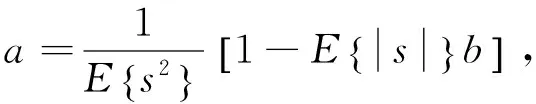
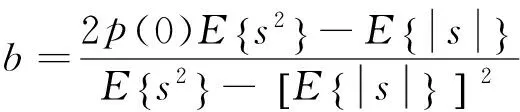
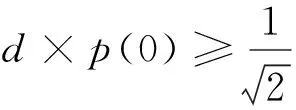
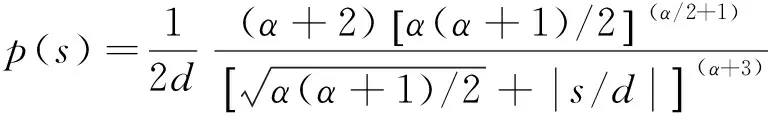
(2)

其中

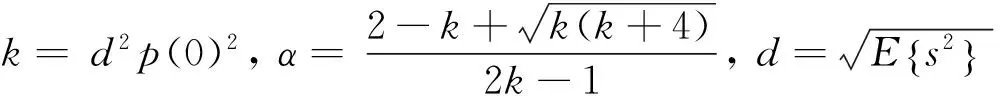
在计算过程中，p(0)估算公式为

(3)

除了上述拟合出信号的概率密度函数再进行定性分析的做法，某信号序列的稀疏程度还可以通过下式(Chang et al., 2005)来度量，公式为

(4)

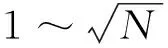
根据上述理论和计算方法，本文首先进行了井下水压裂微地震信号是否具有稀疏分布特征的研究.

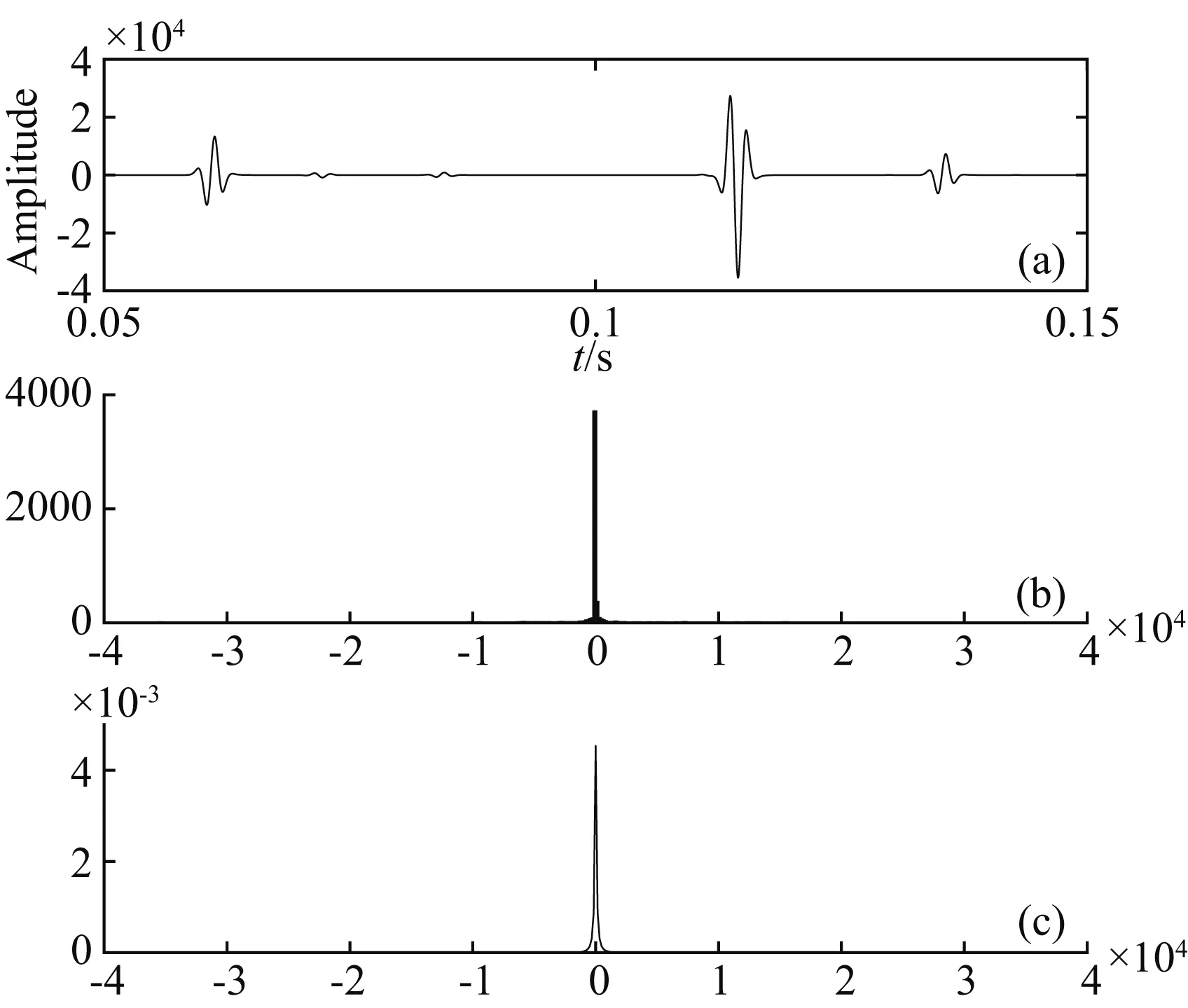
图1　地震信号的稀疏分布特征(a) 合成微地震记录；(b) 信号的统计直方图；(c) 信号的概率密度分布.Fig.1　Sparse distribution feature of seismic signal(a) Synthetic microseismic signal; (b) Singal′s statistical histogram; (c) Singal′s probability density distribution.

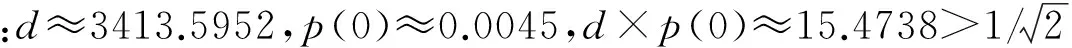
选取不同波形、幅值、衰减程度、组合方式，或不同长度和采样率的井下微震记录按照上述方法进行处理，结果表明拟合出的概率密度函数均具有鲜明的Super-Gaussian分布特征，且稀疏度δ的值均大于作为参考的Laplace分布信号.故利用归纳法可以得出结论：井下水压裂微地震信号在统计学上是服从稀疏分布的.该结论也与前人利用时频稀疏性分析方法得到的研究结果相一致(王鹏等, 2014).

2.2基于稀疏分布特征的井下微地震信号识别与提取方法

明确了井下水压裂微地震信号具有稀疏分布的特征，理论上可以直接采用Hyvarinen提出的稀疏码收缩方法，或者将其结合不同的变换类方法进行处理，如傅氏变换(孟小红等, 2008; 熊登和张剑锋, 2008)、小波变换(高静怀等, 2006; 朱振宇等, 2009)、曲波变换(袁艳华等, 2013; 白兰淑等, 2014)、拉东变换(Zhang et al., 2015)等.在本研究中，选择了将稀疏码收缩方法与小波变换相结合，主要是基于以下考虑：

(1) Hyvarinen提出的稀疏码收缩方法需要首先获得与待处理数据中有效信号成分具有相似分布特征的无噪信号序列，据此来估算正交基.这在针对指定信号类型选择基函数的理论研究中是非常有意义的.但在实际的井下微地震信号处理过程中，由于影响因素复杂多样难以在事先给定一个通用的理想无噪信号序列.通过与小波变换相结合则可以通过优选小波理论中丰富的小波基函数作为正交基对含噪数据进行直接处理.

(2) 在信号特征方面，除了在统计学上具有稀疏分布特征，井下微地震信号本身还是一种频率随时间变化的非平稳信号，对于此类信号小波变换通过伸缩和平移运算可以得到具有时间参数的不同尺度下的小波谱，具有良好的时-频定位特性和多分辨率分析特性，并且其在低频处频率细分、高频处时间细分的特点适宜于突变信号的检测.

(3) 相对于稀疏码收缩方法来说小波变换拥有Mallat快速算法，井下微震监测要处理的数据量很大，并且要求很高的实时性，小波变换的快速计算能力在工业化应用时非常关键.

根据小波理论，信号可以通过小波变换递归地分解为不同级的细节系数和近似系数.经过这一变换过程，相对于规律性不强的非有效信号，有效信号的能量将更加聚集，其分布特征也将在小波系数中体现得更为明显.因此，将稀疏码收缩与小波变换相结合，即将前述针对稀疏分布信号的计算、参数估计方法，转而应用于经过小波分解后不同级的小波系数，并将稀疏码收缩方法中施加的非线性收缩方式作为阈值准则对小波系数进行改造处理.

2.2.1小波基函数的选择

小波基函数的选择是小波理论应用于具体问题时的一个难点，本文以井下水压裂微地震信号为研究对象，选择小波基时主要考虑了以下几个方面： (1) 要与地震子波形状相似； (2) 具有严格的正交性； (3) 具有较窄的紧支集、较快的衰减速度； (4) 由于在本研究中需要优先保证从信噪比极低的监测记录中也能识别和提取出有效地震信号，故强调了紧支撑性而牺牲了部分对于对称性的要求； (5) 要有足够高的消失矩.

综合上述考虑因素并经过试验，最终选择Coiflets系中的coif4小波基和Daubechies系中的db5、db10小波基进行了数值实验、以及后续实际井下微震监测数据的处理.表1列出了Daubechies系和Coiflets系小波基的一些重要性质.

2.2.2对小波系数的改造

选择合适的小波基可以保证经过小波变换分解后有效信号成分在小波系数中更好的聚集，而要实现理想的降噪或信号提取目的，则必须采用恰当的方法对小波系数进行改造.对于具有稀疏分布特征的信号，Hyvarinen根据最大似然原则提出了一种针对稀疏编码的非线性收缩处理方式，在此将其作为阈值准则对小波系数进行处理：

表1　Daubechies和Coiflets小波系的性质Table 1　Nature of Daubechlies and Coiflets wavelets

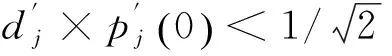
(5)

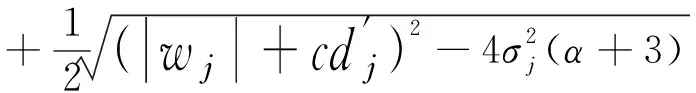
(6)

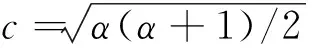
最后利用各级经过改造后的小波细节系数和最高一级的小波近似系数进行反变换，便可重构出时间域的信号处理结果.

3　数值模拟实验

3.1子波提取实验

为了检验前述方法的应用效果，并从多方面进行评价，本次研究首先设计了从含噪信号序列中提取地震子波的实验.

如图2所示，图2a1显示了主频为400 Hz的雷克子波信号的波形图，峰值到时为0.05 s.图2a2为利用短时傅里叶变换(STFT, short-time Fouriertransform)对该段信号进行时频分析得到的时频谱，图2a3为该信号的频谱.图2b1为对前述雷克子波信号按照信号能量/噪声能量=1/10的比例(SNR=-10db)添加高斯白噪声后的含噪信号序列，图2b2和图2b3分别为该含噪信号序列的时频谱和频谱.

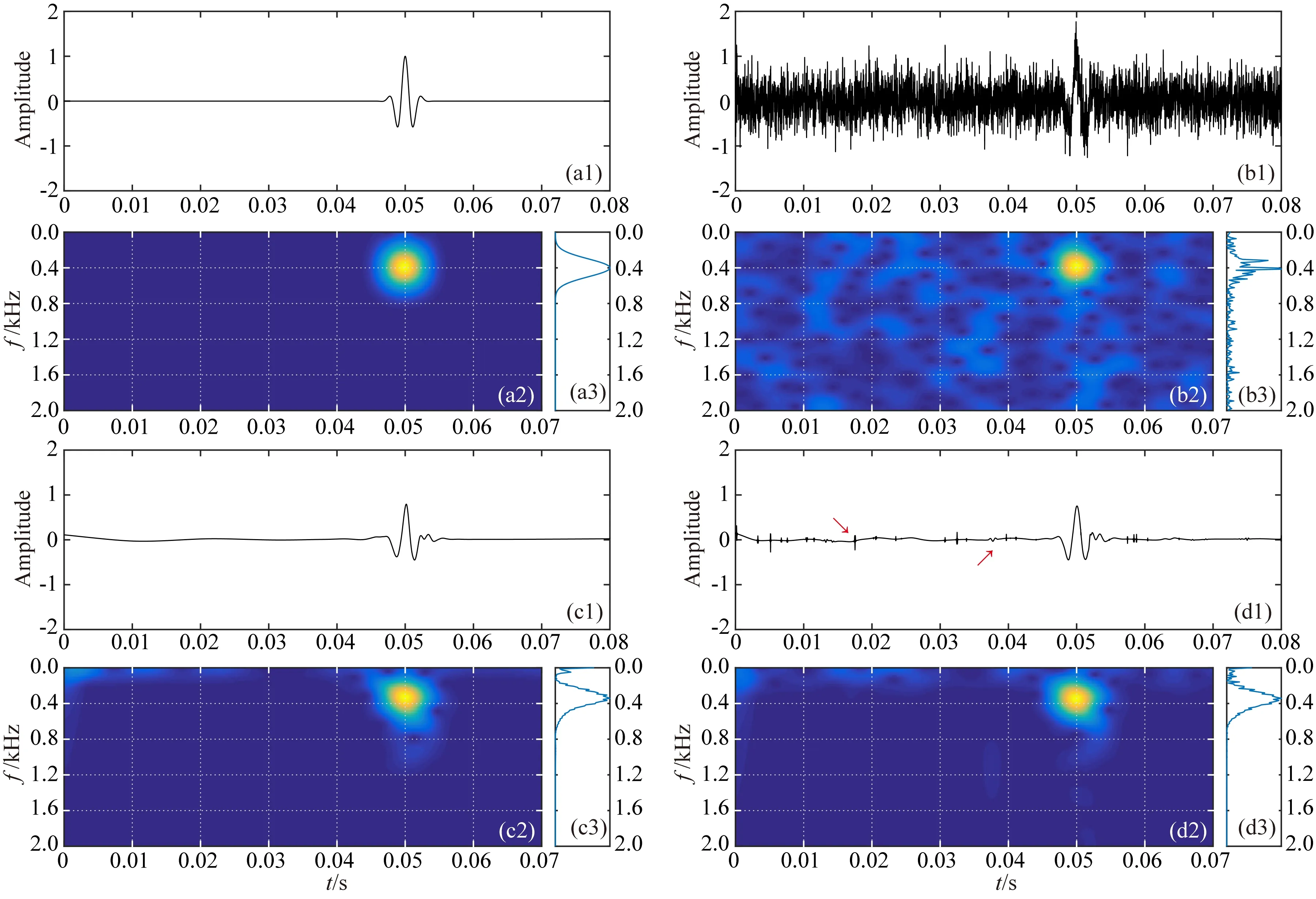
图2　子波提取实验(a) 雷克子波信号(a1)及其时频谱(a2)和频谱(a3)； (b) 含噪信号序列(b1)及其时频谱(b2)和频谱(b3)； (c) 本文方法去噪结果(c1)及其时频谱(c2)和频谱(c3)； (d) 软阈值方法去噪结果(d1)及其时频谱(d2)和频谱(d3).Fig.2　Extraction tests of seismic wavelets(a) Ricker wavelet signal (a1), its time-frequency spectrum (a2), and frequency spectrum (a3)；(b) Noised signal (b1), its time-frequency spectrum (b2), and frequency spectrum (b3)；(c) Result of suggested method (c1), its time-frequency spectrum (c2), and frequency spectrum (c3)；(d) Result of soft-threshold method (d1), its time-frequency spectrum (d2), and frequency spectrum (d3).

参照第2.1节中的讨论，该段雷克子波信号无疑是满足稀疏分布的，因此可以采用本文基于稀疏分布特征的信号识别与提取方法(为了行文方便下文有时将该方法简写为“本文方法”)进行处理.选用coif4小波基，进行10级小波分解、系数改造与重构，得到的处理结果如图2c1所示，图2c2和图2c3分别为该处理结果的时频谱和频谱.可见虽然添加了能量很强的干扰噪声，利用本文方法处理后提取出的地震子波信号无论相位、幅值，亦或频谱、时频谱特征方面都与初始的雷克子波信号(图2a1)非常接近.作为参照，图2d1给出了在小波基函数(coif4)及变换级数(10级)相同的条件下，利用常规的、公认较为优秀的小波软阈值去噪方法对图2b1所示含噪信号序列进行处理的结果.可以看到，软阈值方法的处理结果虽然也能接受，但与图2c1相比，图2d1上多了一些幅值很小、频率较高的“刺状”噪声(如图中红色箭头指示).而且在图2d2揭示的信号时频谱上也分布着更多本不应该存在的能量团.分析造成本文方法和软阈值方法处理结果差别的原因，在于针对具有稀疏分布特征的信号，本文方法采用了更具针对性的处理准则，从而展现出了相应的优势.

3.2抗噪能力测试

作为一种信号的识别与提取方法，算法的抗噪能力测试非常重要，它决定了算法的健壮性和是否具有实用价值.测试内容应当包括当面对低信噪比或者极低信噪比数据时，算法是否还能准确地识别与提取出有效信号，以及能够在多大程度上恢复有效信号.为此，本研究进行了在不同信噪比情况下，检验方法计算效果的抗噪能力测试.为了便于量化所使用的数据为人工合成数据.

井下水压裂微地震事件产生的地震波主频往往高达几百赫兹，远高于常规地震勘探.进行正演模拟时，如此高的主频要求使用非常小的计算网格和时间步长，计算量非常大，以致常规的有限差分数值模拟方法较难达到要求.为此在本研究中利用谱元法求解弹性波动方程(Tromp et al., 2008)，并通过分区并行计算的方法获得了主频为400 Hz的人工合成井下微地震记录，如图3所示.

图3a为0.08 s时刻地震波加速度场的波场快照(X分量)以及相应的震相标识，图3b为最终获得的人工合成地震记录.采用的模型为双层地质模型，模型的速度、密度参数以及界面位置(绿色横线)均如图3a中所示.纵、横波速度和密度参数的设定参考了本次研究实际数据来源工区的测井资料.模拟的微地震事件发生在(120 m,120 m)位置.监测井中检波器间隔为10 m，布设在(320 m,350 m)～(320 m,200 m)处，共16道.检波器横跨地质界面，这种设计增加了合成记录的复杂程度，同时也提高了其代表性.

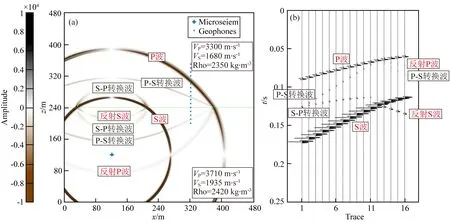
图3　合成地震记录的获得与震相分析(a) 0.08 s时刻地震波加速度场波场快照(X分量)； (b) 合成地震记录.Fig.3　Synthetic seismic record and the wave filed with phase analyse(a) Snapshot of seismic acceleration-field at 0.08 s; (b) Synthetic seismic record.

图4展示了对于SNR=+3 db、0 db、-3 db(相应的有效波能量与噪声能量的比值分别为2∶1、1∶1、1∶2)的高信噪比合成记录利用本文方法处理的结果.选用的小波基均为db5，小波变换级数为5级.可以看到，对于信噪比较高的数据(如本例中SNR≥-3 db的情况)，使用本文方法处理后有效地震信号基本能够完全恢复.

对比原始不含噪声的人工合成记录(图3b)，除了记录右侧0.07～0.09 s范围内，紧随在直达P波之后，能量过于微弱的反射P波和P-S转换波震相在添加噪声后的地震记录图(图4a1、图4b1、图4c1)

和处理结果剖面(图4a2、图4b2、图4c2)中均难以分辨，讨论时不予考虑.其他直达P、S波，在界面处产生的P-S、S-P转换波，以及反射S波等在处理后的地震剖面上均得到了很好地重现.通过图4a3、图4b3、图4c3展示的单道记录(第16道)对比图，可见对于具有高信噪比的含噪记录利用本文方法提取出的有效地震信号与原始不含噪声的地震信号相比，在到时、相位和振幅值方面均达到了高度的吻合.

图5展示了对于SNR=-10 db、-20 db、-30 db(相应的有效波能量与噪声能量的比值分别为1∶10、1∶100、1∶1000)的低信噪比、极低信噪比数据利用本文方法处理后的结果.同样使用db5小波基，小波变换级数为5.

观察图5a1可见，在SNR=-10 db的含噪记录中，除了能量最强的直达S波以外，其余所有震相的波形均被湮没在了噪声之中.经过处理后，在图5a2中，直达P波、S波以及能量相对较强的反射S波震相(图中红色箭头所示)均得到了恢复，但记录左侧的P-S和S-P转换波难以再现.推测这是由于转换波震相的能量较为微弱，它们所处信号段的局部信噪比过低的原因造成的.观察图5a3展示的单道记录对比图，可以看到对于SNR=-10db的情况识别和提取出的有效地震信号在到时和波形方面与原始信号保持了良好的一致性.

图5　低信噪比合成数据降噪试验(a) SNR=-10 db; (b) SNR=-20 db; (c) SNR=-30 db.Fig.5　De-noising tests on low SNR synthetic data

继续提高干扰噪声的能量，如图5b所示.当SNR=-20 db时，从图5b1展示的波形图上可见几乎所有的地震信号都被湮没在了噪声之中.在处理结果图(图5b2)上，直达P波和S波震相能够得到分辨.虽然在图5b3显示的单道数据对比图中，提取出的地震信号的波形已难以与初始信号保持完全一致，但进行对比可以发现此时有效信号的峰值位置依然准确(如图5b3中箭头指示).对于这种情况，根据信号峰值进行到时拾取后，大部分利用P-S波到时差、地震波走时差进行定位的高精度地震定位方法(王晨龙等, 2013)仍然能够发挥作用.

当信噪比低至SNR=-30 db(single energy/noise energy=1/1000)时，如图5c1所示，所有的地震信号均被完全淹没.利用本文方法进行处理后，在处理结果(图5c2)中可以识别出直达S波的影像.观察图5c3可知，此时难以通过单道地震记录进行震相识别和到时拾取，但可借助去噪后地震记录(图5c2)中相邻道信号之间的相似性进行处理.这种情况看似极端，但在本次研究处理大量井下实际生产数据的过程中却占有相当的比例，尤其是对于某些时段来说更是如此.对于此类情况，利用本文方法进行处理，首先可以准确地判断出是否有微地震事件发生；结合相邻道信息进行震相拾取后，再利用传统的根据多道S波到时进行定位的稳健的地震定位算法(周建超和赵爱华, 2012)仍然可以保证对于井下微地震事件的监测不发生疏漏.

4　典型实际井下水压裂微地震数据的处理与分析

为了检验方法在实际数据处理中的应用效果，本次研究利用基于稀疏分布特征的井下微地震信号识别与提取方法处理了大量的实际生产数据.实际井下微地震数据记录类型为三分量记录，共16道检波器接收，总时长约14个小时，采样间隔为0.5 ms，每3 s保存一个记录文件.对于本次数据，在DELL M4800移动工作站上的计算结果表明，处理单个地震文件的平均计算用时约为0.434 s(不包括数据格式转换及I/O开销).从中共识别出可定位的水压裂微地震事件3825个.在此选择了一些有代表性的监测记录用以反映本文方法在实际应用中的效果.

4.1高信噪比井下微震监测数据处理情况

图6和图7展示了利用本文方法对两段具有高信噪比的井下微地震监测记录的处理效果.从不同检波点之间相同震相的到时差来看，它们分别对应着微地震事件发生位置距离监测井接收排列较近(图6)和较远(图7)的两种情况.

可以看到，对于具有较高信噪比的实际井下数据(图6a和图7a)，利用本文方法处理后有效地震信号能够得到非常完整地识别和恢复(图6b和图7b)，干扰噪声则被很好地滤除，经过处理后地震剖面看起来非常干净.对比原始数据和处理结果，有效地震信号的到时、振幅值、相位特征、延续长度等均较为合理，基本观察不到由于处理原因造成的有效波能量损失或波形畸变.参考之前进行的数值实验结果，可以认为在高信噪比情况下，利用本文方法有效地震波可得到几乎无失真地提取和还原.这样的处理结果能够满足后续到时拾取、高精度地震定位(Xue et al., 2015)、甚至全波形反演等方面的研究要求.

在此推测图7中显示的接收到地震信号的数据道较少以及有效信号频率看起来相对较低的原因，是由于微地震信号在相对较远的传播过程中经历了较大程度的吸收衰减，并且相对于低频成分来说信号的高频成分衰减更快的原因造成的.

4.2低信噪比井下微震监测数据处理情况

图8展示了利用本文方法对某时段极低信噪比数据的处理结果.原始记录如图8a所示，从中可以看出对于该段数据背景噪声的能量很强，并且分布于不同的频段；有效地震信号相对而言极其微弱，尤其是在一些局部位置已经被噪声完全湮没.在图8b展示的处理结果中，可以看到在滤除了绝大部分噪声之后，有效地震信号得到了准确地识别和提取(图8a和图8b均使用相同的增益显示).在处理结果剖面上P、S波震相特征明显、可追踪性强、且表现出了明显的双曲线形态.这些特征可以从侧面说明所提取出的地震信号是正确的，而非未处理干净的“噪声残留”.

图7　高信噪比井下微地震记录处理(FFID=00887)(a) 原始数据；(b) 处理结果.Fig.7　Processing of high SNR downhole microseismic record(FFID=00887)(a) Original data; (b) Processing result.

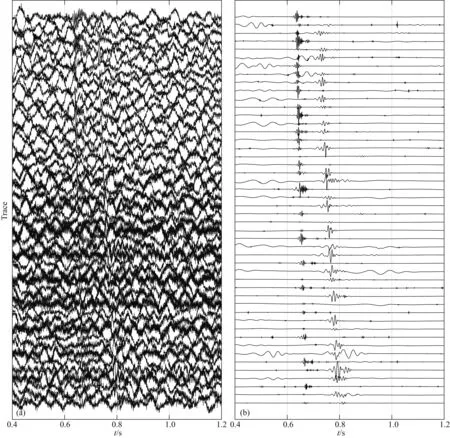
图8　低信噪比井下微地震记录处理(FFID=10009)(a) 原始数据；(b) 处理结果.Fig.8　Processing of low SNR downhole microseismic record(FFID=10009)(a) Original data; (b) Processing result.

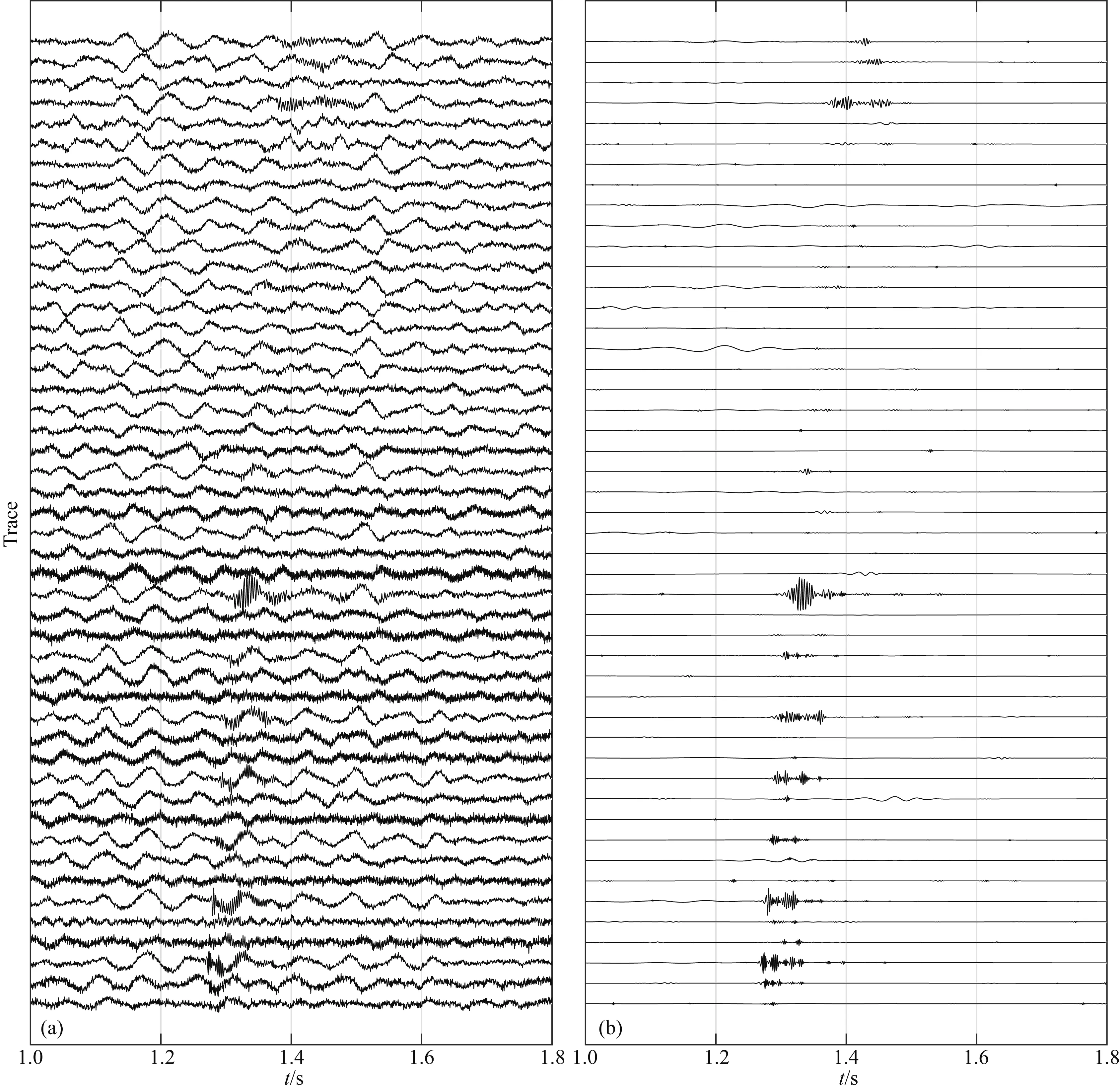
图9　检波器低耦合测段微地震记录处理(FFID=10158)(a) 原始数据；(b) 处理结果.Fig.9　Processing of downhole microseismic record in section of low-coupling dectector(FFID=10158)(a) Original data; (b) Processing result.

参考前文3.2节抗噪能力测试中的实验结果(图5b)，可以认为对于这种极低信噪比数据，虽然不能保证提取出的地震信号与原始地震信号完全一致，但信号峰值位置、到时信息等依然是准确与可靠的.在这种情况下，后续利用P-S波到时差、地震波走时差进行定位的高精度地震定位方法仍然能够很好地发挥作用.因此可以认为这样的处理结果是能够接受的.

4.3检波器低耦合情况下监测数据的处理情况

与进行数值模拟实验时的理想情况不同，在实际的井下微震监测过程中三分量检波器的埋置误差以及与地下介质的耦合情况等都会对监测数据造成较大影响.其表现通常为某时段监测记录的信噪比普遍偏低，或监测记录中部分数据道信号缺失.

图9a便展示了这样一段推测由于检波器耦合不佳造成的低信噪比监测数据.在此难以考量检波器耦合状况对微地震信号本身造成的影响，利用本文方法处理后的结果如图9b所示.可以看到经过处理，地震记录的信噪比得到了很大提高，除去信号缺失的地震道，提取出的有效地震信号双曲线特征明显，满足地震定位条件.

5　结论与讨论

井下微震监测是采用水力压裂法这一低渗油气田和非常规油气田开发核心增产措施时的关键配套技术.从低信噪比甚至极低信噪比的监测数据中准确识别与提取出有效地震信号是后续研究工作的基础和前提.本文提出了基于稀疏分布特征的井下水压裂微地震信号识别与提取方法，进行了理论与实际数据处理研究，取得了良好的效果.

经过分析应用本文方法具有以下几方面的合理性与优势： (1) 井下水压裂微地震信号是一种具有稀疏分布特征的非平稳信号，这从理论上支持了采用基于稀疏分布特征的小波变换类信号处理方法的合理性. (2) 井下微震监测要求很高的实时性，利用成熟的Mallat快速算法可以很好地解决计算效率问题. (3) 应用简单，本文方法几乎所有的计算工作均在程序内部实现，应用时只需简单选择预定的小波基函数和小波变换级数，便可获得令人满意的处理结果.

通过多方面的数值实验以及对某工区大量实际生产数据的处理，证实了本文方法具有抗噪能力强、有效地震信号识别准确可靠、提取信号保真度高等优点，值得进一步的研究和推广.

Bai L S, Liu Y K, Lu H Y, et al. 2014. Curvelet-domain joint iterative seismic data reconstruction based on compressed sensing.ChineseJ.Geophys. (in Chinese), 57(9): 2937-2945, doi: 10.6038/cjg20140919.

Bowman A W, Azzalini A. 1997. Applied Smoothing Techniques for Data Analysis. Oxford: Clarendon Press.

Chang C Q, Ren J Y, Fung P C W, et al. 2005. Novel sparse component analysis approach to free radical EPR spectra decomposition.JournalofMagneticResonance, 175(2): 242-255. Gao J H, Mao J, Man W S, et al. 2006. On the denoising method of prestack seismic data in wavelet domain.ChineseJ.Geophys. (in Chinese), 49(4): 1155-1163. Hyvärinen A. 1999. Sparse code shrinkage: denoising of nongaussian data by maximum likelihood estimation.NeuralComputation, 11(7): 1739-1768. Hyvärinen A, Hoyer P O, Oja E. 1999. Sparse code shrinkage: denoising by nonlinear maximum likelihood estimation.∥ Conference on Advances in Neural Information Processing Systems II. Denver, Colorado, USA, 473-478.

Jiang Y, Chen X, Tao J Y, et al. 2005. The technique of generating super-Gaussian and quasi-random vibration exciting signals.JournalofVibrationEngineering(in Chinese), 18(2): 179-183.

Liu Z W, Sa L M, Wu F R, et al. 2013. Microseismic monitor technology status for unconventional resource E&P and its future development in CNPC.OGP(in Chinese), 48(5): 843-853.

Meng X H, Guo L H, Zhang Z F, et al. 2008. Reconstruction of seismic data with least squares inversion based on nonuniform fast Fourier transform.ChineseJ.Geophys. (in Chinese), 51(1): 235-241.

Tromp J, Komatitsch D, Liu Q Y. 2008. Spectral-element and adjoint methods in seismology.CommunicationsinComputationalPhysics, 3(1): 1-32. Wang C L, Cheng J B, Yin C, et al. 2013. Microseismic events location of surface and borehole observation with reverse-time focusing using interferometry technique.ChineseJ.Geophys. (in Chinese), 56(9): 3184-3196, doi: 10.6038/cjg20130931.

Wang P, Chang X, Wang Y B, et al. 2014. Automatic event detection and event recovery in low SNR microseismic signals based on time-frequency sparseness.ChineseJ.Geophys. (in Chinese), 57(8): 2656-2665, doi: 10.6038/cjg20140824.

Xiong D, Zhang J F. 2008. Table-Driven 2-D non-uniform sampling fast Fourier transform.ChineseJ.Geophys. (in Chinese), 51(6): 1860-1867.

Xue Q F, Wang Y B, Zhan Y, et al. 2015. An efficient GPU implementation for locating micro-seismic sources using 3D elastic wave time-reversal imaging.Computers&Geosciences, 82: 89-97.

Yuan Y H, Wang Y B, Liu Y K, et al. 2013. Non-dyadic curvelet transform and its application in seismic noise elimination.ChineseJ.Geophys. (in Chinese), 56(3): 1023-1032, doi: 10.6038/cjg20130330.

Zhang L L, Wang Y B, Zheng Y K, et al. 2015. Deblending using a high-resolution radon transform in a common midpoint domain.JournalofGeophysicsandEngineering, 12(2): 167-174.

Zhou J C, Zhao A H. 2012. An intersection method for locating earthquakes in 3-D complex velocity models.ChineseJ.Geophys. (in Chinese), 55(10): 3347-3354, doi: 10.6038/j.issn.0001-5733.2012.10.017.

Zhu Z Y, Lv D Y, Sang S Y, et al. 2009. Research of spectrum decomposition method based on physical wavelet transform and its application.ChineseJ.Geophys. (in Chinese), 52(8): 2152-2157, doi: 10.3969/j.issn.0001-5733.2009.08.025.

附中文参考文献

白兰淑, 刘伊克, 卢回忆等. 2014. 基于压缩感知的Curvelet域联合迭代地震数据重建. 地球物理学报, 57(9): 2937-2945, doi: 10.6038/cjg20140919.

高静怀, 毛剑, 满蔚仕等. 2006. 叠前地震资料噪声衰减的小波域方法研究. 地球物理学报, 49(4): 1155-1163.

蒋瑜, 陈循, 陶俊勇等. 2005. 超高斯伪随机振动激励信号的生成技术. 振动工程学报, 18(2): 179-183.

刘振武, 撒利明, 巫芙蓉等. 2013. 中国石油集团非常规油气微地震监测技术现状及发展方向. 石油地球物理勘探, 48(5): 843-853.

孟小红, 郭良辉, 张致付等. 2008. 基于非均匀快速傅里叶变换的最小二乘反演地震数据重建. 地球物理学报, 51(1): 235-241.

王晨龙, 程玖兵, 尹陈等. 2013. 地面与井中观测条件下的微地震干涉逆时定位算法. 地球物理学报, 56(9): 3184-3196, doi: 10.6038/cjg20130931.

王鹏, 常旭, 王一博等. 2014. 基于时频稀疏性分析法的低信噪比微震事件识别与恢复. 地球物理学报, 57(8): 2656-2665, doi: 10.6038/cjg20140824.

熊登, 张剑锋. 2008. 表驱动的二维非规则采样快速傅里叶变换. 地球物理学报, 51(6): 1860-1867.

袁艳华, 王一博, 刘伊克等. 2013. 非二次幂Curvelet变换及其在地震噪声压制中的应用. 地球物理学报, 56(3): 1023-1032, doi: 10.6038/cjg20130330.

周建超, 赵爱华. 2012. 三维复杂速度模型的交切法地震定位. 地球物理学报, 55(10): 3347-3354, doi: 10.6038/j.issn.0001-5733.2012.10.017.

朱振宇, 吕丁友, 桑淑云等. 2009. 基于物理小波的频谱分解方法及应用研究. 地球物理学报, 52(8): 2152-2157, doi: 10.3969/j.issn.0001-5733.2009.08.025.

(本文编辑张正峰)

Downhole microseismic signal recognition and extraction based on sparse distribution features

LI Wen1,2,3, LIU Yi-Ke1*, LIU Bao-Jin1，3

1KeyLaboratoryofShaleGasandGeoengineering,InstituteofGeologyandGeophysics,ChineseAcademyofSciences,Beijing100029,China2UniversityofChineseAcademyofSciences,Beijing100049,China3GeophysicalExplorationCenter,ChinaEarthquakeAdministration,Zhengzhou450002,China

On account of working environment, downhole microseismic monitoring records usually contain much noise, i.e. having low SNR (signal to noise ratio). Thus recognizing and extracting effective signals is a priority for subsequent work.

Microseismic monitoring; Hydraulic fracturing; Sparse distribution feature; Signal recognition and extraction; Wavelet transform; De-noise

10.6038/cjg20161030.

国家自然科学基金(41430321)、国家自然科学基金(41374138)、中国地震局地球物理勘探中心青年优秀科技人才专项(SFGEC2014006)联合资助.

李稳,男,1983年生,博士研究生,主要从事地震波传播与成像研究及勘探地震数据处理方法研究.E-mail:liwen_work@163.com

刘伊克,男,研究员,主要从事勘探地球物理和地震学研究.E-mail:ykliu@mail.iggcas.ac.cn

10.6038/cjg20161030

P631

2016-02-02，2016-06-30收修定稿

李稳, 刘伊克, 刘保金. 2016. 基于稀疏分布特征的井下微地震信号识别与提取方法. 地球物理学报，59(10):3869-3882,

Li W, Liu Y K, Liu B J. 2016. Downhole microseismic signal recognition and extraction based on sparse distribution features.ChineseJ.Geophys. (in Chinese),59(10):3869-3882,doi:10.6038/cjg20161030.