地层衰减对地震波速度逆散射反演的影响研究

段晓亮, 翟鸿宇, 王一博, 杨慧珠

1 清华大学工程力学系, 北京　100084 2 中科院地质与地球物理研究所, 北京　100029



地层衰减对地震波速度逆散射反演的影响研究

段晓亮1, 翟鸿宇2, 王一博2, 杨慧珠1

1 清华大学工程力学系, 北京100084 2 中科院地质与地球物理研究所, 北京100029

在利用地震波数据进行地球物理反演时,地层对地震波的吸收衰减效应会对地层物性参数的准确反演产生较大的影响,因此利用黏弹性声波方程进行反演更符合实际情形.本文在考虑地层衰减效应进行频率空间域正演模拟的基础上，提出基于黏弹性声波方程的频率域逆散射反演算法并对地震波传播速度进行反演重建，在反演过程中分别用地震波传播复速度和实速度来表征是否考虑地层吸收衰减效应.基于反演参数总变差的正则化处理使反演更加稳定，在反演中将低频反演速度模型作为高频反演的背景模型进行逐频反演，由于单频反演过程中背景模型保持不变，故该方法不需要在每次迭代中重新构造正演算子，具有较高的反演效率；此外本文在反演过程中采用了基于MPI的并行计算策略，进一步提高了反演计算的效率.在二维算例中分别对是否考虑地层吸收衰减效应进行了地震波速度反演，反演结果表明考虑衰减效应可以得到与真实模型更加接近的速度分布结果，相反则无法得到正确的地震波速度重建结果.本文算法对复杂地质模型中浅层可以反演得到分辨率较高的速度模型，为其他地震数据处理提供比较准确的速度信息，在地层深部由于地震波能量衰减导致反演分辨率不太理想.

反演； 地震波速度； 逆散射； 衰减

1　引言

地震波在地层中传播时由于受到地层的吸收衰减作用而产生能量耗散,因此用黏弹性介质模型描述地震波的传播过程更加符合实际情形，黏弹性介质中传播的地震波携带了介质的相关物性参数信息.地球从大尺度的地质构造到小尺度的孔隙结构都存在物性参数的不均匀性,实际地层的岩石通常是由岩石骨架和各种黏性的孔隙填充物组成的多相黏弹性介质(Kuster and Toksöz,1974)，由于岩石的内摩擦作用以及填充物的黏滞作用，地震波在介质中传播时将会发生速度频散和衰减现象(王海洋等，2012).相关研究表明地下介质对地震波的吸收衰减作用与介质的孔隙度、孔隙填充物有密切联系(Winkler and Nur,1982; Pride et al.,2004; Müller et al.,2010).地层对地震波的吸收衰减效应用品质因子Q来表征,它是介质非完全弹性的度量,是地球介质的本质属性之一,Varela研究了这种衰减规律(Varela et al., 1993)，Jacobsen研究了沉积岩中地震波衰减和速度弥散以及频率之间的相互关系(Jacobsen, 1987).

地球物理反演算法大致可以分为线性反演和非线性反演两类：在线性反演中，各种不同的线性近似被引入到反演算法中，例如Born近似(Oristaglio, 1985)、Rytov近似(Devaney, 1981)等，这些算法只在某些特定情况下有效.非线性反演算法没有改变反演问题的非线性本质，例如全波形反演方法(Symes, 2008；张文生等，2015)、遗传算法(Stoffa and Sen, 1991)、神经网络方法(Zhang and Paulson, 1997)等，这些算法通过不断迭代的方式对地下构造进行反演成像.地球物理反演可以在时间域进行(Moghaddam and Chew, 1992)，也可以在频率域进行(Pratt, 1999)，Tarantola对考虑衰减效应的波形反演理论进行了研究(Tarantola, 1998)，地震波在地层介质中的传播速度是地球探测活动中非常重要的参数之一,在黏弹性介质速度反演研究方面，龙桂华等利用失配函数二范数最小准则，用预条件梯度类方法对黏弹性声波介质的速度结构进行了逐频反演(龙桂华等，2009)，Causse等在黏弹性介质全波形反演过程中引入了两种预处理方法(Causse et al., 1999)，取得了较好的效果.

随着地震波勘探活动范围的不断扩大，勘探目标越趋复杂，在地表接收不到某些构造的反射波，但可以接收到散射波，基于散射波场的反演方法是地球物理领域中一种非常有效的反演方法之一(黄联捷和杨文采，1991；杨晓春等，2005).Van den Berg等进行了基于电磁散射波场的反演研究(Van den Berg and Kleinman, 1997; Van den Berg et al., 1999; Van den Berg and Abubakar,2001)，该方法是源积分类方法的拓展(Habashy et al., 1994)，该反演算法以背景模型是均匀介质为基本前提，Abubakar将该方法进一步扩展为适应非均匀背景介质的情形 (Abubakar et al., 2008).在最初的电磁波反演问题中，反演尺度范围较小，没有考虑电磁波在介质中的吸收衰减效应，反演过程基于完全弹性声波方程.在地震波勘探活动中，地球介质尺度非常大，吸收衰减效应将不能忽略，本文反演过程基于黏弹性声波方程, 更加符合地震波在地球介质中的真实传播过程.

2　正演模拟

2.1控制方程

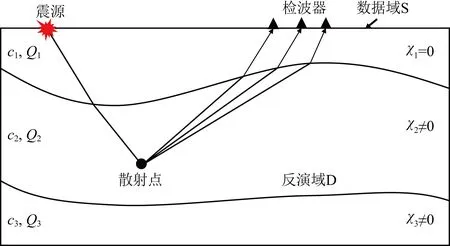
图1　逆散射问题示意图Fig.1　Schematic diagram of inverse scattering problem

逆散射反演问题示意图如图1所示，我们定义反演域D和数据域S，其中炮点和检波器位于数据域S中，两者的组合称为总计算区域T.地层对地震波的吸收衰减效应用品质因子Q来表征，地层不同位置对应不同的Q值，c表示地震波传播速度.相对于真实速度模型，假设有一个背景模型，引入反演变量，该变量表示已知背景模型和未知真实模型物性参数之间的相对扰动量.反演域中的每一个网格点都可以看作是相对于背景模型的一个散射点，通过求解一个最优化问题来不断更新，从而得到模型的速度分布.

本文假设反演过程中介质密度ρ为常数，考虑地层吸收衰减效应时地震波总波场pj(r)在频率-空间域满足Helmholtz方程为

(1)

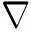
(2)

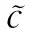
(3)

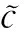
(4)

利用复速度与复波数间的关系，我们可以正演得到受地层吸收衰减影响的波场数据，本文参考频率-空间域9点差分格式模拟地震波在吸收衰减介质中的传播过程(Jo et al., 1996).

2.2吸收边界条件

在对地震波传播过程进行有限差分数值模拟过程中，为了有效吸收入射到计算区域边界的波场，采用吸收边界条件是必要的.PML吸收边界条件是非常有效的吸收边界反射的方法(Berenger, 1994)，本文使用复数延伸坐标PML吸收边界条件来消除计算边界区域产生的人工反射(Chew and Weedon, 1994).在吸收边界区域式可以写为

(5)

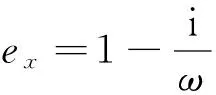
3　反演算法

将考虑地层吸收衰减的地震波传播总波场写成背景波场和散射波场之和为

(6)

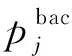
(7)

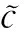
将式从式中减去，得到考虑吸收衰减效应时散射波场满足的方程为

(8)

此处引入一个变量wj(r)，公式为

(9)

(10)

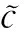
传统反演算法的优化目标函数为检波器接收数据与正演模拟数据的残差值，本文方法的优化目标函数由数据域误差和反演域误差以及基于反演参数总变差值的正则项组合而成，反演域误差项和正则项的引入在一定程度上提高了算法的稳定性和抗干扰性.算法利用非线性共轭梯度法(Fletcher and Reeves, 1964; Gilbert and Noedal, 1992)最小化目标优化函数从而不断更新w，总波场p以及的值，最终得到地下介质的速度参数分布.

本文算法的反演目标优化函数为

(11)

(12)

利用非线性共轭梯度法，w迭代更新公式为

(13)

vj,0=0，

(14)

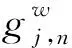
(15)

更新完w以后，利用式(6)、式(8)更新总波场p值，然后利用非线性共轭梯度法更新值，公式为

(16)

正则化目标优化函数Fn(,wj)关于的梯度为

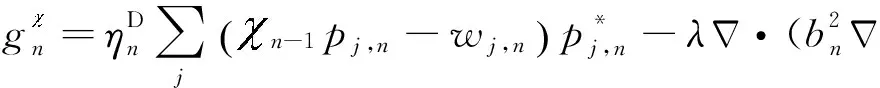
(17)

其中

(18)

4　数值算例

本文利用二维Marmousi模型对反演算法进行测试，该速度模型非常复杂，真实速度模型见图2a，模型速度范围为1500～5500 m·s-1, 在x和z方向被离散为384×122个等间距网格，网格间距为15 m，震源采用主频为7.5 Hz的雷克子波.我们采用四个频率(4 Hz,12 Hz,20 Hz,24 Hz)依次进行反演，地震数据由均匀分布于地表的64炮产生，炮间距为90 m，检波点布置在地表所有网格点上.假设初始背景模型速度分布为由上到下线性增加，速度范围为1500～4200 m·s-1，初始背景模型见图2b.

在实际地震波勘探中，地表检波器接收到的波场数据是受地层吸收衰减作用后的波场数据，首先我们在反演过程中使用的正演算子考虑了地层的吸收衰减效应，反演中将低频反演结果作为下一个高频反演的背景模型.单频反演结果见图3所示，从图中可以看出反演频率较低时，反演结果给出了模型的大尺度构造，随着反演频率的逐渐增加，重建速度模型的分辨率也逐步提高，Marmousi模型中的一些小尺度细节构造也能够较好的重建.

图4所示为考虑地层吸收衰减效应的各频率反演速度模型与真实速度模型、初始速度模型在地表1485 m和3435 m位置处沿深度方向的速度比较图，从速度比较曲线看出，初始速度模型为线性递增的，4 Hz反演结果在初始模型的基础上给出了真实模型的大尺度轮廓，12 Hz、20 Hz、24 Hz反演结果不断逼近真实速度模型.在中浅层反演模型与真实模型基本完全一致，由于Marmousi模型深度1400 m以下的速度纵横向变化剧烈，包含大量薄地层结构，异常高速体下面又隐藏有低速体构造，从反演结果可以看出，模型深部反演结果并不理想，这是由于地震波在地层中传播时由于地层吸收衰减效应使得地震波能量不断减弱，地震波频谱中高频成分的衰减较低频成分更为严重，导致反演结果的分辨率降低.

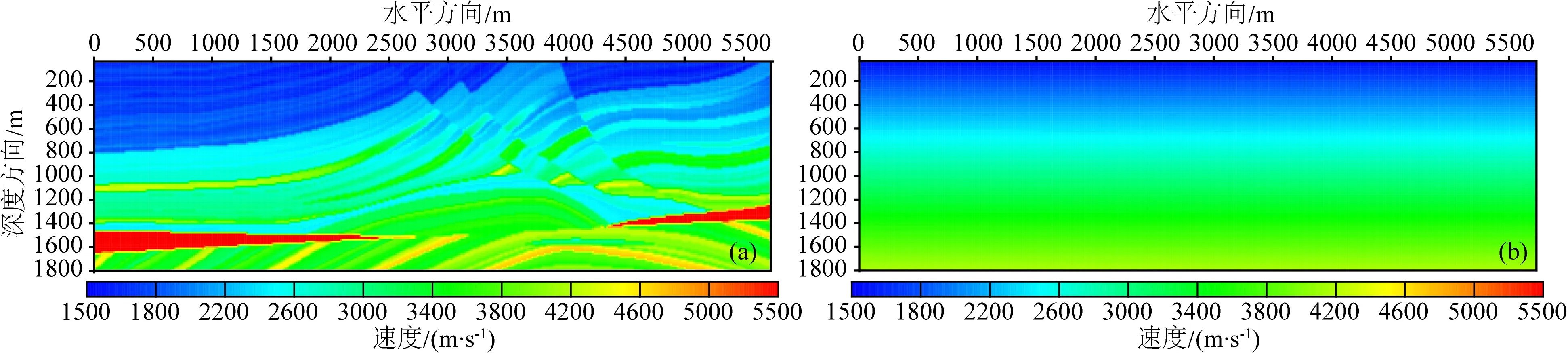
图2　(a)真实Marmousi速度模型; (b)初始线性背景模型Fig.2　(a) True Marmousi velocity model； (b) Initial linear background model

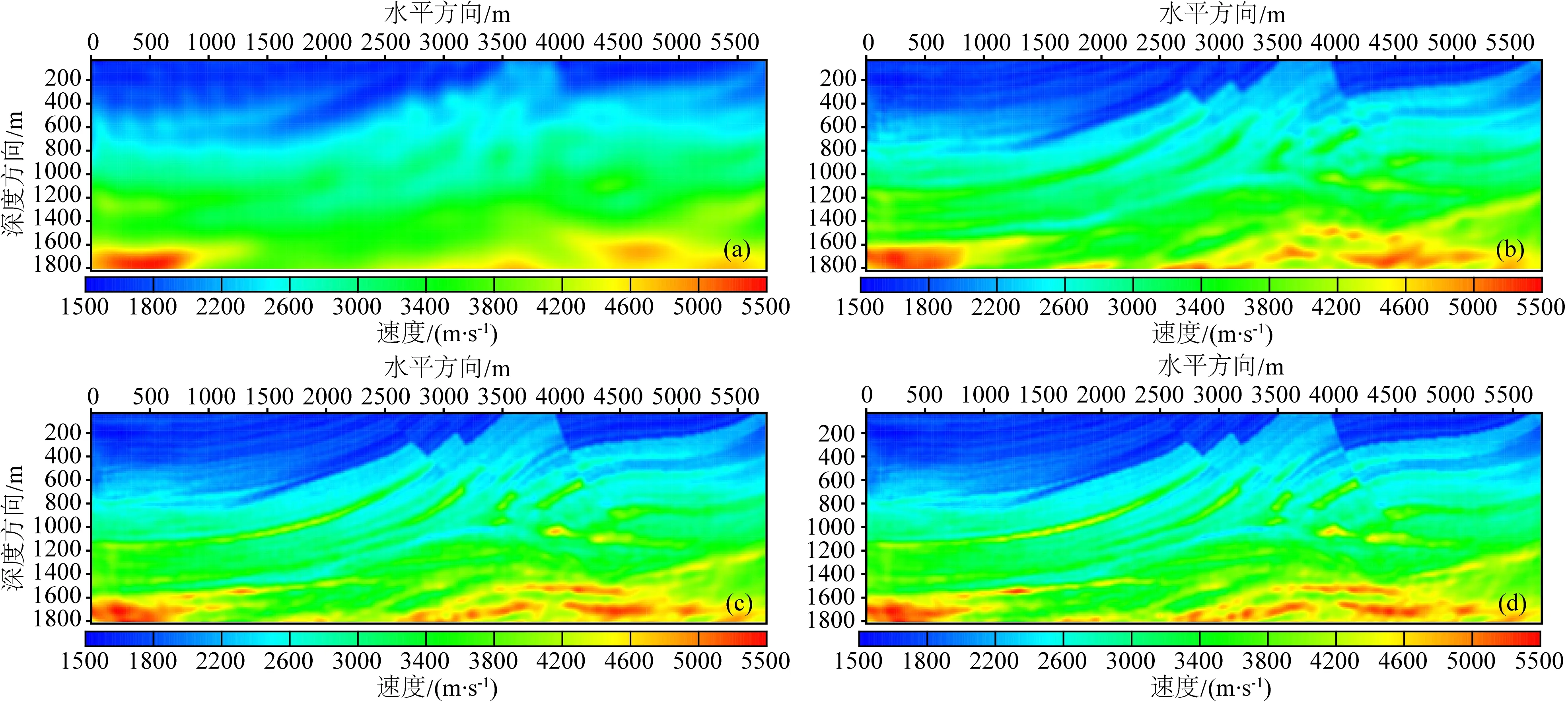
图3　考虑地层吸收衰减效应反演速度模型(a) 4Hz; (b) 12Hz; (c) 20Hz; (d) 24Hz.Fig.3　Reconstructed velocity model by the inversion algorithm considering attenuation effect at frequencies of (a) 4 Hz, (b)12 Hz, (c) 20 Hz, and (d) 24 Hz

图4　考虑衰减效应反演模型与真实模型速度比较曲线(a) 1485 m; (b) 3435 m.Fig.4　Comparison of velocities between true Marmousi model and inversion model considering attenuation effect at surface positions of (a)1485 m and (b)3435 m

作为对比，本文对在反演过程中不考虑地层吸收衰减效应的反演结果进行了分析，即在反演过程中正演算子不包含品质因子Q的影响，反演结果如图5所示，可以看出，由于在反演过程中所采用的正演算子不符合地震波在地层中的真实传播过程，与前面反演结果相比，在4 Hz时反演得到了模型的大尺度速度结构，但随着反演频率的提高，反演所得速度模型的分辨率没有得到相应提高，12 Hz、20 Hz、24 Hz反演结果几乎一样，反演结果与真实模型有较大差距.

图6所示为相同地表水平位置处，不考虑地层吸收衰减效应时沿深度方向的速度比较曲线，可以看出反演速度模型与真实模型有较大差距，随着反演频率的提高，模型细节尺度的构造无法得到重建，甚至在模型浅层也没能给出正确的重建速度模型结果.

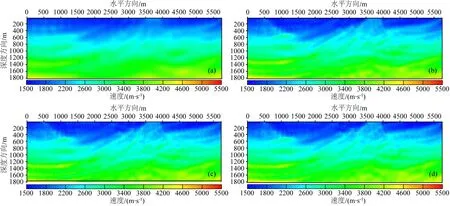
图5　不考虑地层吸收衰减效应反演速度模型(a) 4 Hz; (b) 12 Hz; (c) 20 Hz; (d) 24 Hz.Fig.5　Reconstructed velocity model by the inversion algorithm without considering attenuation effect at frequencies of (a) 4 Hz, (b) 12 Hz, (c) 20 Hz, and (d) 24 Hz

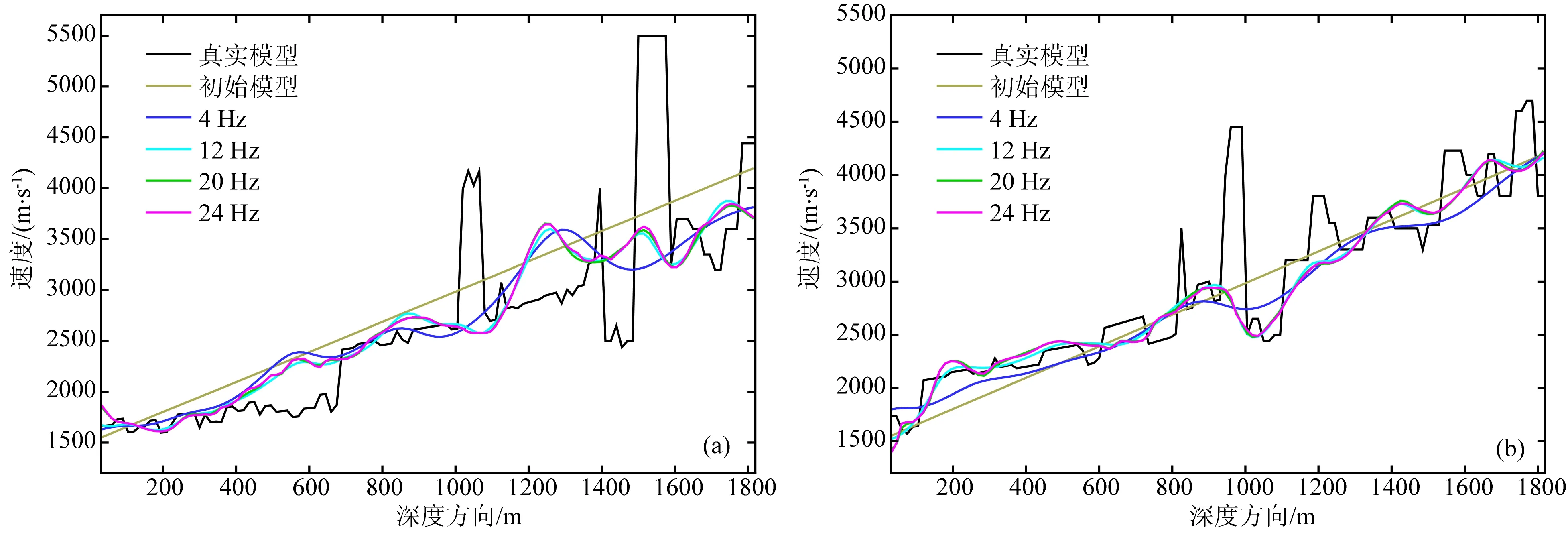
图6　不考虑衰减效应反演模型与真实模型速度比较曲线(a) 1485 m; (b) 3435 m.Fig.6　Comparison of velocity between true Marmousi model and inversion model without considering attenuation effect at surface positions of (a) 1485 m and (b) 3435 m

图7为地表3435 m处沿深度方向真实模型与两者24 Hz反演结果的速度分布比较曲线，由于地表检波器接收到的波场数据为受地层吸收衰减作用以后的数据，可以看出考虑地层衰减效应的反演结果更加接近于真实速度模型，因为反演过程中的正演算子更符合地震波在地层中的真实传播过程，相反，反演中不考虑衰减效应则无法得到正确的速度重建结果.

为了进一步提高反演计算效率，本文采用基于MPI的并行算法对多炮地震波数据进行并行计算，反演过程中使用了10个独立进程，单频反演所耗计算时间约为3 h.图8所示为反演迭代过程中目标函数残差值随迭代次数的变化曲线，可以看出计算过程收敛很快，计算效率较高.

背景模型的选取对反演精度会产生一定的影响，在前面线性背景模型的基础上，本文又采用将原模型进行平滑处理后作为初始背景模型进行了逐频反演，初始背景模型如图9所示，此外为检验方法的抗噪能力，反演过程中在每个单频反演中将检波器散射波数据加入5%的随机噪声，公式为

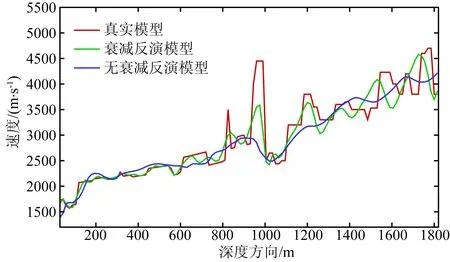
图7　是否考虑地层衰减效应24 Hz反演模型与真实模型速度比较曲线Fig.7　Comparison of velocity between true Marmousi model and inversion model with and without considering attenuation effect at frequency of 24 Hz

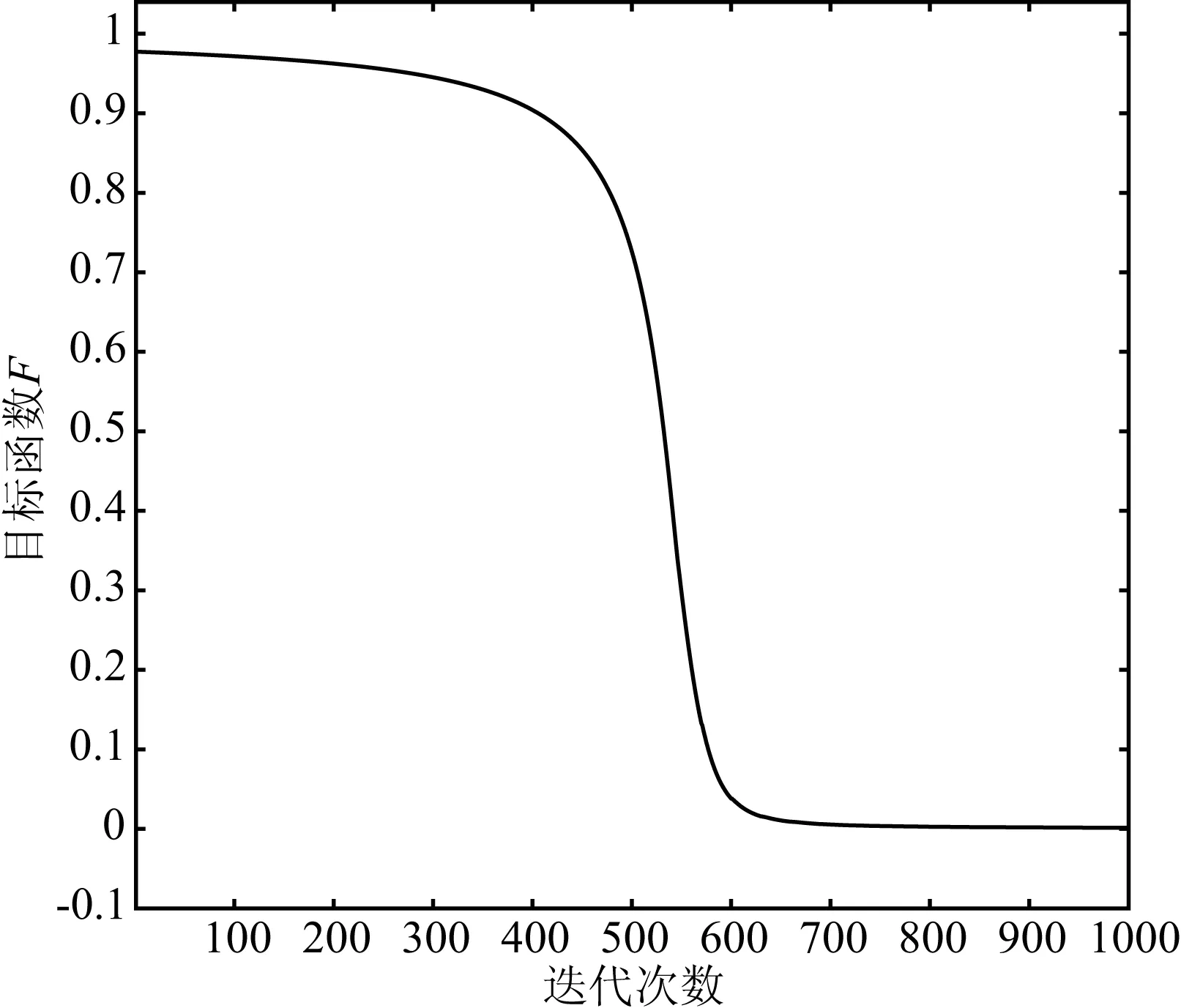
图8　反演迭代残差收敛曲线图Fig.8　Convergence curve of residuals from inversion iteration

(19)

从图10可以看出，选取平滑化初始背景模型得到的反演重建结果可以得到模型的细节尺度构造，与前面线性背景模型反演结果相比，重建模型深部的反演精度和分辨率有了一定的提升，图11为模型地表1485 m、2235 m、3435 m、 4485 m处速度分布随地层深度的变化曲线，从曲线比较中也可以得到相同的结论.此外从反演结果可以看出，在地震波数据包含随机噪声的情况下，由于正则化处理使得反演方法具有一定的抗噪能力.

我们利用式(20)对不同频率反演重建模型相对于真实模型的反演误差进行统计分析，表1为两种不同初始背景模型反演结果相对于真实模型的误差值，公式(20)为

(20) 表1　不同背景模型反演精度 Table1　Inversion precisions using different background models

从表1可以看出，背景模型的选取对最终反演结果的精度将产生较大的影响，选择平滑化背景模型反演精度比线性背景模型高，表明背景模型的选取越接近于真实模型，反演结果精度越高.

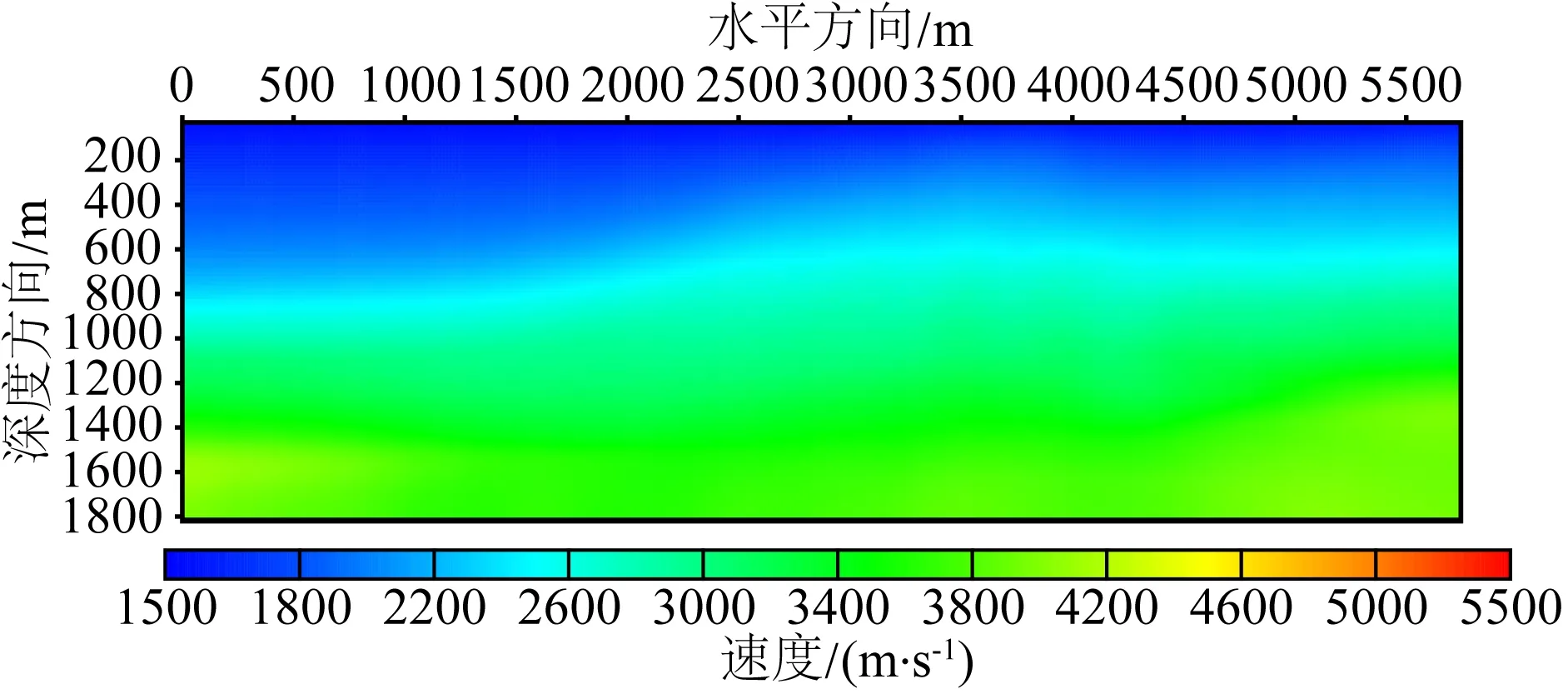
图9　平滑化初始背景模型Fig.9　Smoothed initial background model

图10　平滑化初始背景模型反演速度模型(a) 4 Hz; (b) 12 Hz; (c) 20 Hz; (d) 24 Hz.Fig.10　Reconstructed velocity model using smoothed initial background model at frequencies of (a) 4 Hz, (b) 12 Hz, (c) 20 Hz, and (d) 24 Hz

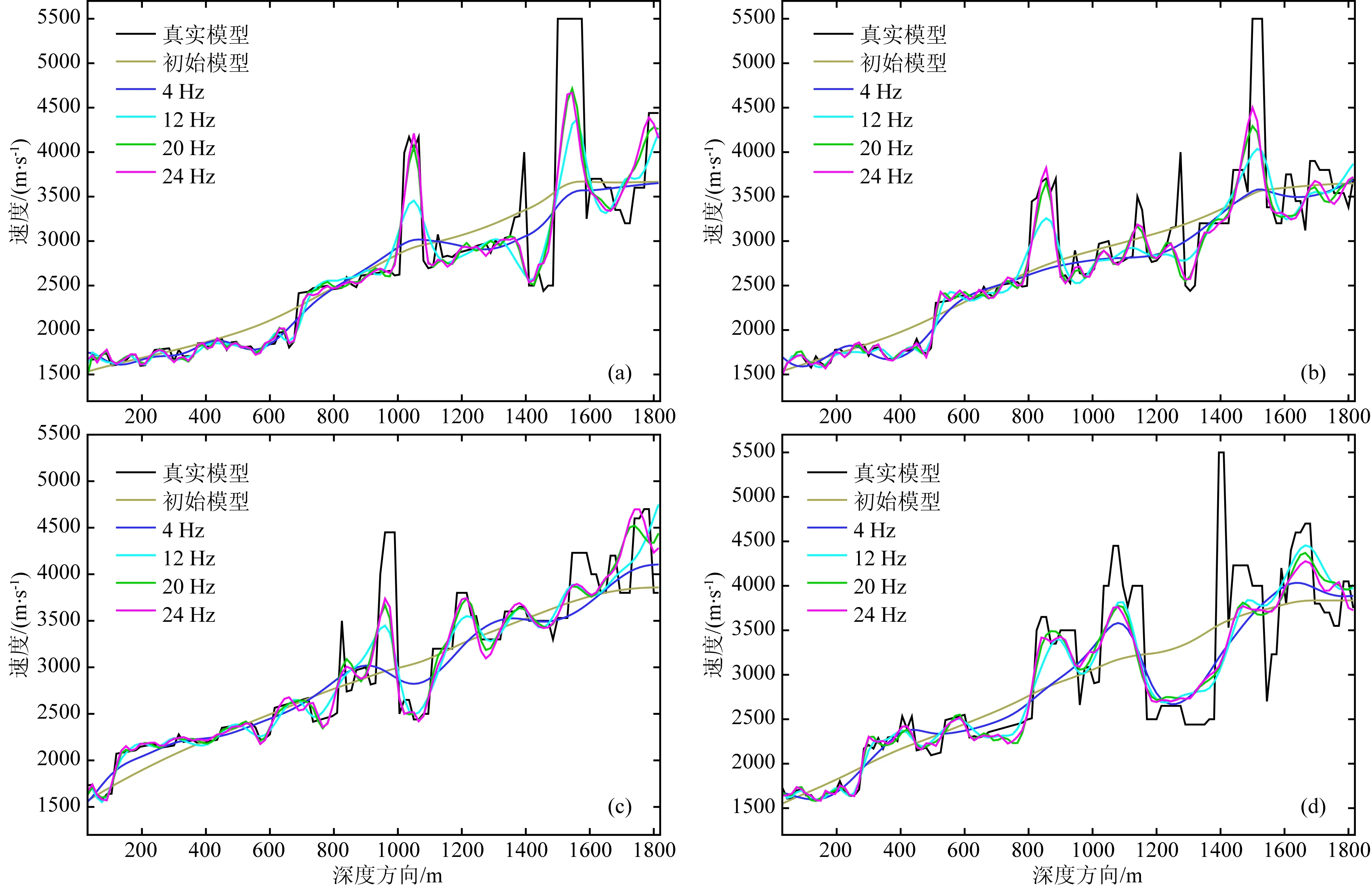
图11　平滑化初始背景重建速度模型与真实速度模型比较曲线(a) 1485 m; (b) 2235 m; (c) 3435 m; (d) 4485 m.Fig.11　Comparison of velocity between true Marmousi model and inversion model using smoothed initial background model considering attenuation effect at surface positions of (a)1485 m, (b) 2235 m, (c) 3435 m, and (d) 4485 m

5　结论

地层对地震波的吸收衰减效应是地球介质的固有属性之一，地表检波器接收到的地震波数据是经过地层吸收衰减作用之后的波场数据，地层的吸收衰减效应对于地球内部物性构造的准确反演会产生较大的影响，如果在反演过程中不考虑这一效应，就无法得到正确的地层速度模型，导致对地层结构做出错误的判断，本文基于黏弹性声波方程的逆散射反演方法更接近于真实情形.本文在考虑地层衰减效应的基础上，对地震波速度进行反演研究，反演结果在地层中浅层分辨率较高，在地层深部由于地震波能量的衰减导致反演重建模型分辨率不太理想.同时背景模型的选取对反演结果的精度会产生一定的影响，背景模型越接近真实模型，反演结果精度越高，在实际地震勘探过程中利用其他勘探手段对地质模型进行初探，选择较为接近真实地层结构的背景模型，可以得到更高精度的反演结果.

地球的地层结构非常复杂，同时影响地震波传播过程的吸收衰减效应也很复杂，对于衰减吸收的有关特性还有待进一步的深入研究，本文假设品质因子Q与地震波速度之间满足一定的经验关系，后续研究可以进一步推广到地震波速度和地层品质因子Q同时反演的情形以及探寻如何提高地层深部反演分辨率的有效措施.

Abubakar A, Hu W, Van den Berg P M, et al. 2008. A finite-difference contrast source inversion method.InverseProblems, 24(6): 065004.

Berenger J P. 1994. A perfectly matched layer for the absorption of electromagnetic waves.JournalofComputationalPhysics, 114(2): 185-200.

Causse E, Mittet R, Ursin B. 1999. Preconditioning of full-waveform inversion in viscoacoustic media.Geophysics, 64(1): 130-145.

Chew W C, Weedon W H. 1994. A 3D perfectly matched medium from modified Maxwell′s equations with stretched coordinates.MicrowaveandOpticalTechnologyLetters, 7(13): 599-604.

Devaney A J. 1981. Inverse-scattering theory within the Rytov approximation.OpticsLetters, 6(8): 374-376.

Fletcher R, Reeves C M. 1964. Function minimization by conjugate gradients.ComputerJournal, 7(2): 149-154.

Gilbert J C, Noedal J. 1992. Global convergence properties of conjugate gradient methods for optimization.SIAMJournalonOptimization, 2(1): 21-42.

Habashy T M, Oristaglio M L, de Hoop A T. 1994. Simultaneous nonlinear reconstruction of two-dimensional permittivity and conductivity.RadioScience, 29(4): 1101-1118. Huang L J, Yang W C. 1991. Inversion of the acoustic wave equation by inverse scattering in a medium of linear reference velocity.ActaGeophysicaSinica(in Chinese), 34(1): 89-98.

Jacobsen R S. 1987. An investigation into the fundamental relationships between attenuation, phase dispersion, and frequency using seismic refraction profiles over sedimentary structures.Geophysics, 52(1): 72-87.

Jo C H, Shin C, Suh J H. 1996. An optimal 9-point, finite-difference, frequency-space, 2-D scalar wave extrapolator.Geophysics, 61(2): 529-537. Kuster G T, Toksöz M N. 1974. Velocity and attenuation of seismic waves in two-phase media: part 1. Theoretical formulations.Geophysics, 39(5): 587-606.

Long G H, Li X F, Zhang M G, et al. 2009. Visco-acoustic transmission waveform inversion for velocity structure in space-frequency domain.ActaSeismologicaSinica(in Chinese), 31(1): 32-41.

Moghaddam M, Chew W C. 1992. Nonlinear two-dimensional velocity profile inversion using time domain data.IEEETransactionsonGeoscienceandRemoteSensing, 30(1): 147-156. Müller T M, Gurevich B, Lebedev M. 2010. Seismic wave attenuation and dispersion resulting from wave-induced flow in porous rocks: a review.Geophysics, 75(5): 75A147-75A164. Oristaglio M L. 1985. Accuracy of the Born and Rytov approximations for reflection and refraction at a plane interface.J.Opt.Soc.Am, 2(11): 1987-1993.

Pratt R G. 1999. Seismic waveform inversion in the frequency domain: Part I—Theory, and verification in a physical scale model.Geophysics, 64(3): 888-901.

Pride S R, Berryman J G, Harris J M. 2004. Seismic attenuation due to wave-induced flow.JournalofGeophysicalResearch, 109: B01201.

Ravaut C, Operto S, Improta L, et al. 2004. Multiscale imaging of complex structures from multifold wide-aperture seismic data by frequency-domain full-waveform tomography: Application to a thrust belt.GeophysicalJournalInternational, 159(3): 1032-1056.

Stoffa P L, Sen M K. 1991. Nonlinear multiparameter optimization using genetic algorithms: inversion of plane-wave seismograms.Geophysics, 56(11): 1794-1810. Symes W W. 2008. Migration velocity analysis and waveform inversion.GeophysicalProspecting, 56(6): 765-790.

Tarantola A. 1988. Theoretical background for the inversion of seismic waveforms including elasticity and attenuation.PureandAppliedGeophysics, 128(1-2): 365-399.

Tian S R. 1990. Estimation of Q value in inverse Q filtering with Li formula.OilGeophysicalProspecting(in Chinese), 25(3): 354-361.

Van den Berg P M, Abubakar A. 2001. Contrast source inversion method: state of art.ProgressinElectromagneticsResearch, 34: 189-218.

Van den Berg P M, Kleinman R E. 1997. A contrast source inversion method.InverseProblems, 13(6): 1607-1620.

Van den Berg P M, Van Broekhoven A L, Abubakar A. 1999. Extended contrast source inversion.InverseProblems, 15(5): 1325-1344.

Varela C L, Rosa A L R, Ulrych T J. 1993. Modeling of attenuation and dispersion.Geophysics, 58(8): 1167-1173.

Wang H Y, Sun Z D, Chapman M. 2012. Velocity dispersion and attenuation of seismic wave propagation in rocks.ActaPetroleiSinica(in Chinese), 33(2): 332-342.

Winkler K W, Nur A. 1982. Seismic attenuation: Effects of pore fluids and frictional-sliding.Geophysics, 47(1): 1-15.

Yang X C, Li X F, Zhang M G. 2005. The fixed point principles of nonlinear seismic scattering inversion.ProgressinGeophysics(in Chinese), 20(2): 496-502.

Zhang W S, Luo J, Teng J W. 2015. Frequency multiscale full-waveform velocity inversion.ChineseJ.Geophys. (in Chinese), 58(1): 216-228. Zhang Y C, Paulson K V. 1997. Magnetotelluric inversion using regularized Hopfield neural networks.GeophysicalProspecting, 45(5): 725-743.

附中文参考文献

黄联捷, 杨文采. 1991. 参考波速线性变化时的声波方程逆散射反演. 地球物理学报, 34(1): 89-98.

龙桂华, 李小凡, 张美根等. 2009. 频率域粘弹性声波透射波形速度反演. 地震学报, 31(1): 32-41.

田树人. 1990. 用李氏经验公式估算反Q滤波中的Q值. 石油地球物理勘探, 25(3): 354-361.

王海洋, 孙赞东, Chapman M. 2012. 岩石中波传播速度频散与衰减. 石油学报, 33(2): 332-342.

杨晓春, 李小凡, 张美根. 2005. 地震波散射非线性反演的不动点理论研究. 地球物理学进展, 20(2): 496-502.

张文生, 罗嘉, 滕吉文. 2015. 频率多尺度全波形速度反演. 地球物理学报, 58(1): 216-228.

(本文编辑张正峰)

Effect of stratigraphic attenuation on inverse-scattering seismic velocity inversion

DUAN Xiao-Liang1, ZHAI Hong-Yu2, WANG Yi-Bo2, YANG Hui-Zhu1

1DepartmentofEngineeringMechanics,TsinghuaUniversity,Beijing100084,China2InstituteofGeologyandGeophysics,ChineseAcademyofSciences,Beijing100029,China

The attenuation effect can influence the precision of inversion of Earth′s physical properties when solving geophysical inverse problems utilizing seismic data. Therefore using the viscoelastic acoustic wave equation is more suitable for the actual situation. In this paper, based on seismic forward modeling considering the attenuation effect in the frequency-space domain, the inversion algorithm with inverse scattering based on viscoelastic acoustic equation is applied in the frequency domain to reconstruct seismic velocity distribution. Real or complex velocity is used individually in the inversion process depending on whether the earth attenuation effect is considered. Meanwhile the regularization of inversion parameter′s total variation makes this inversion approach more stable. Frequency-divided inversion strategy is adopted, the lower frequency inversion result is set as the background model of higher frequency inversion, and the background model remains constant during the inversion process for a particular frequency. So this inversion method does not need to reconstruct the forward operator in each iteration, which makes it more efficient. In order to improve the efficiency of inversion calculation further, the MPI parallel computing strategy is used in the procedure of inversion. In a 2D numerical example, the inversion algorithm is applied with and without considering the attenuation effect respectively. The results from the former approach is closer to the real velocity model, while the latter cannot match the real model. This algorithm can achieve high-resolution velocity reconstruction results for complex geological models at shallow and middle layers, and can provide accurate velocity information for other seismic data processing. While the inversion resolution is not ideal for a deep layer due to the attenuation of seismic energy.

Inversion; Seismic velocity; Inverse scattering; Attenuation

10.6038/cjg20161023.

国家自然科学基金(41174094)和国家科技重大专项(2011ZX05004-003)联合资助.

段晓亮,男,博士研究生,主要从事地震波反演方面的研究. E-mail:gfkjdxdxl@aliyun.com

10.6038/cjg20161023

P631

2015-06-02，2016-03-21收修定稿

段晓亮, 翟鸿宇, 王一博等. 2016. 地层衰减对地震波速度逆散射反演的影响研究. 地球物理学报，59(10):3788-3797,

Duan X L, Zhai H Y, Wang Y B, et al. 2016. Effect of stratigraphic attenuation on inverse-scattering seismic velocity inversion.ChineseJ.Geophys. (in Chinese),59(10):3788-3797,doi:10.6038/cjg20161023.