基于频域衰减的时域全波形反演

郭雪豹， 刘洪， 石颖

1 中国科学院地质与地球物理研究所中国科学院油气资源研究重点实验室， 北京　100029 2 中国科学院地质与地球物理研究所， 北京　100029 3 东北石油大学， 大庆　163318



基于频域衰减的时域全波形反演

郭雪豹1,2， 刘洪1,2， 石颖3

1 中国科学院地质与地球物理研究所中国科学院油气资源研究重点实验室， 北京100029 2 中国科学院地质与地球物理研究所， 北京100029 3 东北石油大学， 大庆163318

时域全波形反演由于采用了全频段信息，因此在迭代过程中不同波长的信息不能由低到高的逐步重建，极易陷入局部极小值.本文通过分频段的方式，对地震数据做正反傅里叶变换，利用频域指数衰减的方法逐级分离出地震数据中的高频成分，在时域上实现由低频向高频的波形反演，从而降低了反演的非线性，使不同波长的信息得到稳步恢复.同时，在高频成分衰减的过程中，后至波的能量也被削弱，由此也降低了深层反射在初始反演过程中的干扰.整个反演仅增加对数据做正反傅里叶变换过程，相较于混合域反演，无需提取全部波场的相应频率成分.在计算效率方面，利用GPU进行加速，并采用CUDA自带函数库中cufft来提高计算效率.通过对Marmousi模型测试，验证了所述方法的有效性.

时域全波形反演；频域衰减；低频；GPU

1　引言

全波形反演是获取地下参数的重要手段之一，其主要通过最小化观测数据与预测数据的残差来得到高精度的地下参数.Tarantola(1984,1986)起初是在时域上实现了声波的全波形反演，随后被其应用到弹性波中.全波形反演是一个高度非线性问题，限于计算压力，无法在实际应用中通过全局最优化的方法得到最优解，而普遍采用局部优化的方法.因此，反演的效果很大程度上取决于初始模型的选择.许多地球物理学家对此问题进行研究，以降低反演对初始速度模型的依赖.Biondi和Almomin(2012)借助层析来获得一个较好的初始速度.Almomin和Biondi (2012)采用波动方程偏移速度分析的方法.Bunks(1995)提出了多尺度的反演策略以降低反演的非线性.Pratt(1999a,1999b)、Brenders和Pratt(2007)将全波形反演应用到频域，并发展了由低频向高频的反演策略.Shin和Cha(2008,2009)提出了拉普拉斯域全波形反演，即便采用线性初始模型也可以得到一个好的反演结果.在这些方法中，多尺度反演大都需要低频信息去恢复模型中的长波长分量.而针对常规地震数据中的低频缺失，Wu等(2013,2014)和Luo等(2013)也提出包络反演，并将其应用到全波形反演中以弥补低频的缺失.

最小化残差本质上是一个迭代的过程，在每次迭代过程中，都需要计算对应模型参数的正传波场和残差的反传波场，相关来计算梯度，因此波场模拟的效率决定了全波形反演的计算效率.对于二维情况来说，频域可以采用直接法进行求解，并且可以多炮并行处理，较时域方法具有明显的优势.但对于三维情况，频域求解变得十分困难，因此，通常在时域完成三维反演.而对于时域波场模拟而言，GPU的特点使得其十分适用于这种大规模的并行计算，Moghaddam(2013)将GPU应用到全波形反演(Yang et al.,2015)中，Boonyasiriwat等人(2010)将其应用于逆时偏移(Yang et al.,2014; Shin et al.,2014; 李博等,2010; 刘红伟等,2011; 刘守伟等,2013)中，石颖等人(2010,2013)则将其用于多次波消除的加速计算中.

本文采用了一种基于频域衰减的时域全波形反演方法.其主要通过对观测数据进行高频衰减来达到在时域上实现由低频向高频的反演.在频域衰减的同时，后至波的能量也在一定程度上被衰减，由此也降低了深层反射在初始反演过程中的干扰.与传统时域全波形反演相比，实现了由低频到高频、由浅层到深层的反演，并同时具有时域正演可高度并行的优势，可直接应用于三维.与混合域全波形反演相比，无需提取全部波场的相应频率成分，仅需对地震记录做傅里叶变换即可.本文算法基于GPU进行加速，并采用CUDA自带函数库的cufft，从而保证算法的稳定高效.通过对Marmousi模型进行测试，验证了本文方法的有效性.

2　基本原理

2.1时域全波形反演基本理论

常密度声波方程可表示为如下形式：

(1)

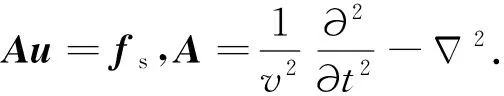
因此，接收点处残差为

(2)

其中，ucal和uobs分别代表计算得到的地震记录和实际观测地震记录，xs和xr分别为震源坐标和检波点坐标.

(2)式在最小二乘意义下的目标函数为

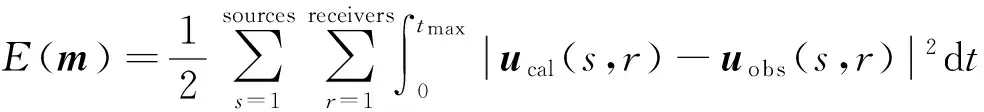
(3)

其中，m为待反演的参数.

参数更新公式：

(4)

其中，在第k+1次迭代中步长αk和方向dk可以分别表示如下：

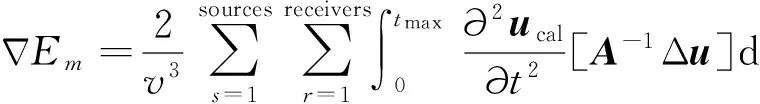
(5)

为补偿照明，梯度归一化公式(Gauthieretal.,1986;Baietal.,2014;Shinetal.,2001)为

(6)

其中，γ为稳定性系数.为了减少噪音干扰，本文在梯度计算后，采用高斯平滑方法压制噪音.

2.2频域衰减

频域衰减公式为

Δu′(xs,xr,t)=

IFFT[FFT[ucal(xs,xr,t)-uobs(xs,xr,t)]G(f)]，

(7)

其中，FFT和IFFT分别为正快速傅里叶变换和反快速傅里叶变换，G(f)为衰减函数，f为频率，Δu′(xs,xr,t)为衰减后的波场数据残差.

本文中采取的衰减函数为

(8)

其中，Q为频域衰减因子，其随着频率的增加而增加.本文采用的是e指数衰减，也可采用其他形式的衰减函数.

2.3GPU_CUFFT

GPU的引入能够在极大程度上提高并行算法的计算效率(Yang et al.,2014; Shin et al.,2014; 李博等,2010; 刘红伟等,2011; 刘守伟等,2013; 石颖等, 2010, 2013; Yang et al.,2015; Boonyasiriwat et al., 2010).本文算法本身搭建在GPU平台下，并通过存储器优化，进一步提高计算过程中的数据读取速度，使得计算效率得到明显提升.

文中所述的频域衰减，需要对多炮地震数据做傅里叶变换，这一过程的计算效率对整个算法的计算效率有较大影响.由于整个算法利用GPU进行加速，因此最好将这一变换过程定义在GPU上进行，这样不仅能够减少数据的读写，也可充分利用GPU并行计算的能力.在这里对GPU的离散傅里叶变换(以下简称CUDA_DFT)与利用GPU库的cufft进行对比，可以看出利用CUDA库函数的CUFFT相较于CUDA_DFT，计算优势明显.

计算速度对比见表1(以一炮767道，每道2800采样点为例)，完成40炮计算时，CUFFT较CUDA_DFT计算效率提高约49倍.

表1　CUDA_DFT与CUFFT计算机时对比Table 1　Contrast of cost of CUDA_DFT and CUFFT

3　模型测试

本文采用Marmousi模型测试所述方法，Marmousi模型如图1所示，纵、横向网格点数分别为251和767，网格间距为12 m，雷克子波主频为10 Hz，时间采样间隔1.5 ms，采样点数为2800.设计21炮震源激发，第一炮位于深度36 m，自左向右36 m位置处，向右每隔456 m放一炮.每炮767个检波器接收，检波器深度36 m，自左向右沿横向依次排列，检波器间距12 m.反演初始速度为真实速度平滑后的结果，如图2所示.地震正演得到的第5炮和第10炮的炮集记录如图3所示.

图1　Marmousi模型Fig.1　Marmousi model

图2　初始速度模型Fig.2　Initial model

首先不考虑频域衰减，即在无任何衰减情况下反演，迭代100次，200次，300次的结果如图4所示.观察易知，随着迭代次数的增加，其反演结果逐渐趋于稳定.对比速度模型可以看出，其反演结果并不理想，尤其在浅部存在较强的噪音干扰.由此可以看出，即便采用平滑后的真实速度模型，时域的全频带反演没有逐步的反演出不同的波长分量，依旧会使结果陷入局部极小值.

图3　炮集记录(a) 第5炮地震记录; (b) 第10炮地震记录.Fig.3　Shot gathers(a) The fifth shot gather; (b) The tenth shot gather.

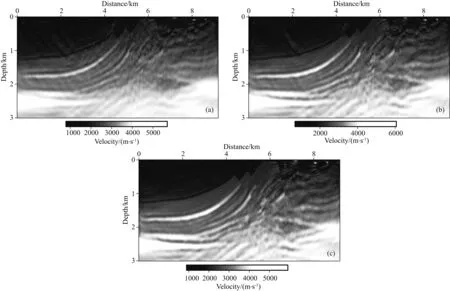
图4　传统时域反演(a) 迭代100次; (b) 迭代200次; (c) 迭代300次.Fig.4　Results of conventional FWI(a) 100 iterations; (b) 200 iterations; (c) 300 iterations.

图5为不同迭代次数的单道对比图，当迭代次数超过100次后，虽然反演依旧向真实值趋近，但随着迭代次数的增加，这种改善越来越小，收敛速度变慢，并趋近于局部极小值，没有收敛到全局最优解.在700 m以上的浅部，当迭代次数达到300时，已经基本与真实速度吻合或逐渐逼近.但随着深度的增加，其收敛程度明显降低，并与真实速度存在较大的偏差，说明时域的全频段反演对深层影响更大.

而后采取频率衰减来进行反演，Q分别取10,20,40,80,0(0代表不做任何衰减)，Q为10时，迭代40次；Q为20时，迭代40次；Q为40时，迭代40次；Q为80时，迭代40次；不衰减时，迭代140次，同样迭代300次，每次迭代均以上一次迭代后的结果为初始速度，结果分别如图6所示，对比可以看出，由于逐级分离出地震记录的高频成分，将其数据限制在低频端，降低了高频成分对反演的影响，使得不同的波长分量得以逐级反演出来.从图6a中可以看出，仅40次迭代，浅部形态就已经基本反演出来.并且随着衰减程度的降低，在浅层精度提高的同时，深部形态也逐渐趋于真实.

在频域衰减过程中由于采用CUDA自带的库函数，保证了对地震记录做正反傅里叶变换的计算效率，每次迭代仅增加约2 s.不同迭代次数单道对比如图7和图8所示，图9为不同迭代次数对比图.频域衰减幅度较大时，少量迭代即可快速收敛，与真实速度吻合较好，随着迭代次数的增加，深层较浅层改善明显.当无衰减40次迭代时，收敛速度已趋于稳定.继续迭代140次后，反演结果变化较小.并且对比衰减下的深浅层可以看出，衰减参数直接作用于记录也消弱了后至波对浅层反演干扰，实现了由浅层到深层的反演，提高了深层反演的精度.

图5　4800 m处单道对比图(a) 迭代100次; (b) 迭代200次; (c) 迭代300次; (d) 不同迭代次数对比.Fig.5　Contrast of single traces between different iterations (Distance=4800 meters)(a) 100 iterations; (b) 200 iterations; (c) 300 iterations; (d) Contrast of different iterations.

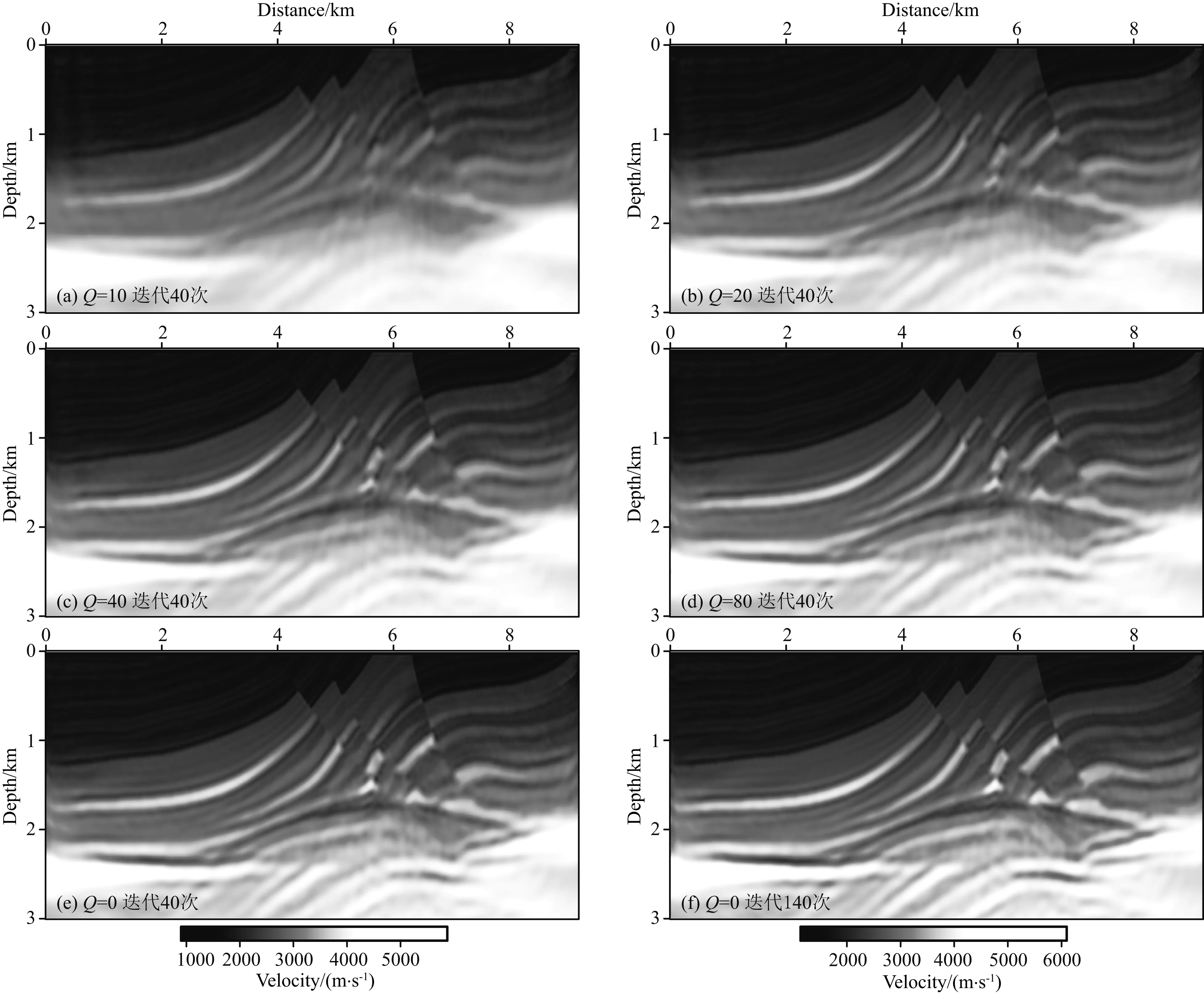
图6　频域衰减反演结果(a) Q=10迭代40次; (b) Q=20迭代40次; (c) Q=40迭代40次; (d) Q=80迭代40次; (e) Q=0迭代40次; (f) Q=0迭代140次.Fig.6　Results of FWI using frequency damping(a) 40 iterations (Q=10); (b) 40 iterations (Q=20); (c) 40 iterations (Q=40);(d) 40 iterations (Q=80); (e) 40 iterations (Q=0); (f) 140 iterations (Q=0).

为了进一步对比迭代效果，将无衰减300次迭代结果与逐级衰减得到的结果相对比，单道对比如图10和图11所示.可以看出，Q为10时，曲线大致趋势已与真实速度开始吻合，在浅部一些突变构造上幅度虽然有所缺失，但位置却较无衰减300次迭代的结果更加准确.并且在深部吻合的更好.随着衰减程度的减弱，当Q为40时，已经与真实速度的位置贴近.当迭代次数继续增加时，深层开始慢慢改善，与真实速度的差异慢慢减小.而无衰减300次迭代的结果在深度依旧保留了一定的误差.

频域衰减后，不同衰减因子的单道信号匹配图，如图12和13所示，分别为偏移距2400 m处的单道衰减0～1 s、3～4 s部分.对比图12a、12b、12c、12d可以看出，当Q逐渐增大时，地震记录中的高频成分被逐级的剥离，仅保留需要频段成分的地震记录，类似于频域的由低频向高频反演，大大减少了高频成分对反演的影响，降低了波形错位的可能.对比图13a、13b、13c、13d，在频域衰减过程中，后至波被一定程度地消弱，也降低了后至波在反演初始阶段对浅层反演的影响，等同于由浅层至深层反演.

4　结论

本文将频域衰减应用于时域全波形反演，以此来实现由低频到高频的逐步反演，并在频域衰减的同时，后至波的能量也在一定程度上被削弱，即频域衰减也同时压制了深层反射，实现由浅层到深层的反演.当衰减程度较大时，仅需少量迭代即可得到一个较好的结果，很大程度上减少了波形错位现象，提高了收敛速度.在计算效率方面，采用GPU进行加速，利用CUFFT实现频域衰减，因此计算效率方面得到有效保证.本文方法属于时域反演，但其避免了传统时域方法全频带反演带来的局部极小值问题.与混合域、Laplace-Fourier域全波形反演相比，不存在其他域的波场计算，完全建立在时域的基础上，并且由于采用了一个频段的信息，反演更为稳健，在选取参数方面也更为灵活.同时，本文方法也保留了时域方法在三维方面的优势.

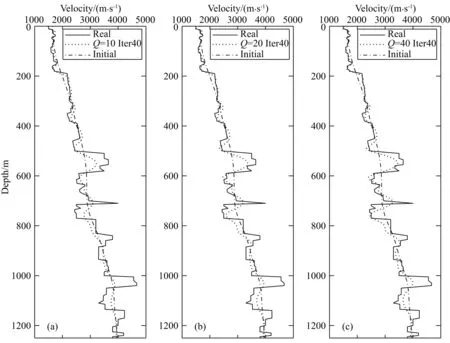
图7　4800 m处单道对比(a) Q=10迭代40次; (b) Q=20迭代40次; (c) Q=40迭代40次.Fig.7　Contrast of single traces between real and Q (Distance=4800 meters).(a) 40 iterations (Q=10); (b) 40 iterations (Q=20); (c) 40 iterations (Q=40).

图8　4800 m处单道对比(a) Q=80迭代40次; (b) Q=0迭代40次; (c) Q=0迭代140次.Fig.8　Contrast of single traces between real and different Q(Distance=4800 meters).(a) 40 iterations (Q=80); (b) 40 iterations (Q=0); (c) 140 iterations (Q=0).

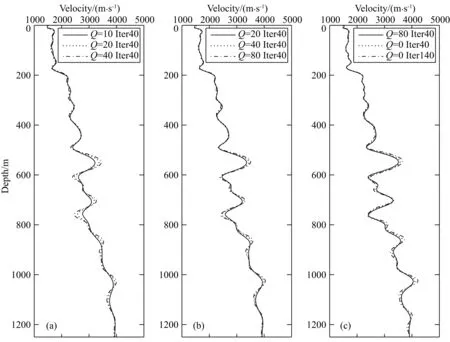
图9　4800 m处单道不同迭代次数对比(a) Q=10, Q=20, Q=40单道对比; (b) Q=20, Q=40, Q=80单道对比; (c) Q=80, Q=0, Q=0单道对比.Fig.9　Contrast of single traces between different Q values (Distance=4800 meters)(a) Contrast of single traces (Q=10, Q=20, Q=40); (b) Contrast of single traces (Q=20, Q=40, Q=80); (c) Contrast of single traces (Q=80, Q=0, Q=0).

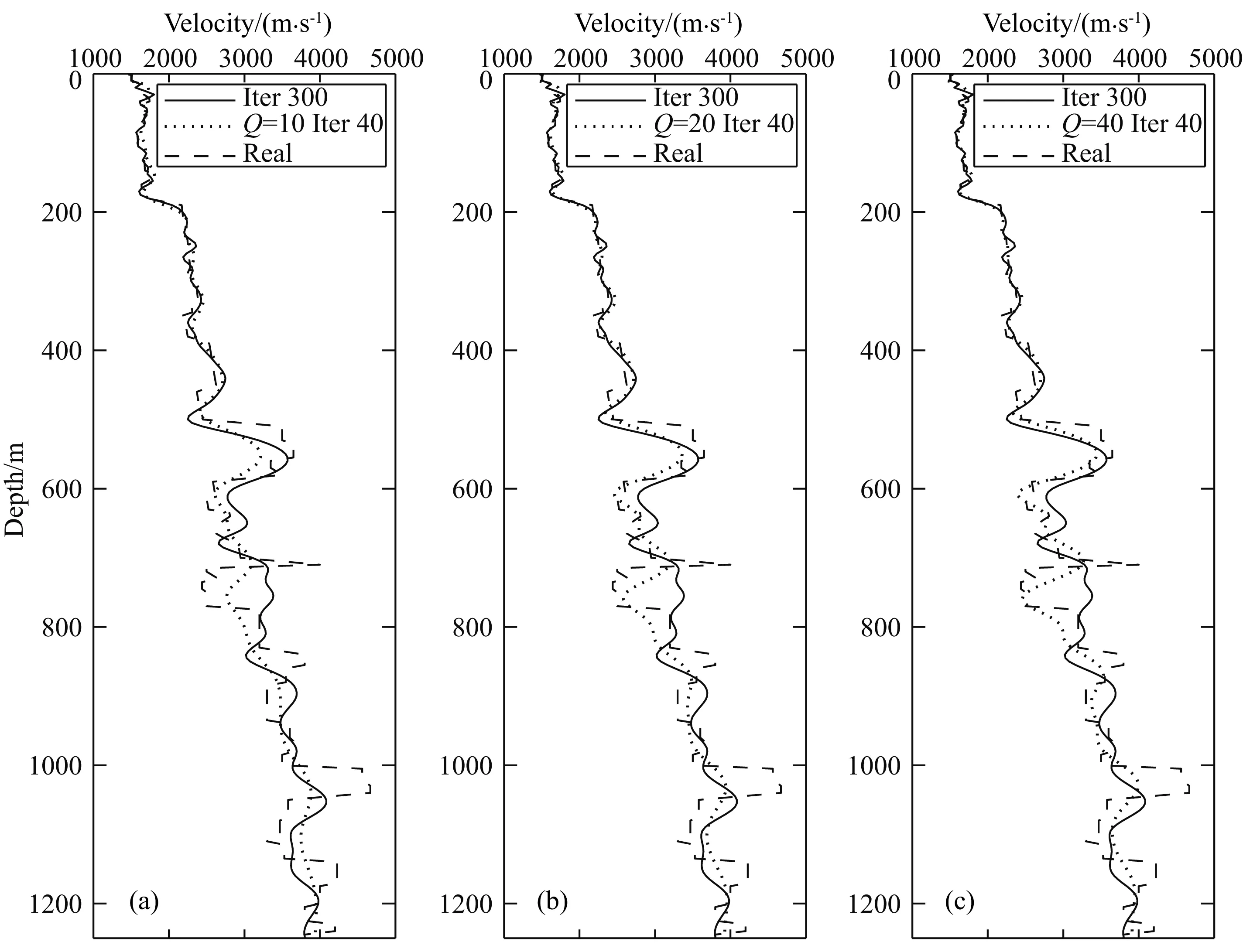
图10　4800 m处两种方法单道对比(a) 原始方法迭代300次与Q=10迭代40次对比; (b) 原始方法迭代300次与Q=20迭代40次对比; (c) 原始方法迭代300次与Q=40迭代40次对比.Fig.10　Contrast of single traces between two methods (Distance=4800 meters).(a) Contrast of singe traces (300 iterations of conventional method and 40 iterations of Q=10); (b) Contrast of singe traces (300 iterations of conventional method and 40 iterations of Q=20); (c) Contrast of singe traces (300 iterations of conventional method and 40 iterations of Q=40).

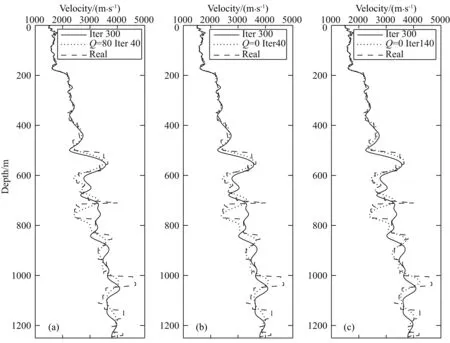
图11　4800 m处两种方法单道对比(a) 原始方法迭代300次与Q=80迭代40次对比; (b) 原始方法迭代300次与Q=0迭代40次对比; (c) 原始方法迭代300次与Q=0迭代140次对比.Fig.11　Contrast of single traces between two methods (Distance=4800 meters).(a) Contrast of singe traces (300 iterations of conventional method and 40 iterations of Q=80); (b) Contrast of singe traces (300 iterations of conventional method and 40 iterations of Q=0); (c) Contrast of singe traces (300 iterations of conventional method and 140 iterations of Q=0).

图12　2400 m处0～1 s单道对比(a) Q=0与Q=10单道对比; (b) Q=0与Q=20单道对比; (c) Q=0与Q=40单道对比; (d) Q=0与Q=80单道对比.Fig.12　Contrast of single traces (Distance=2400 meters, 0～1 s)

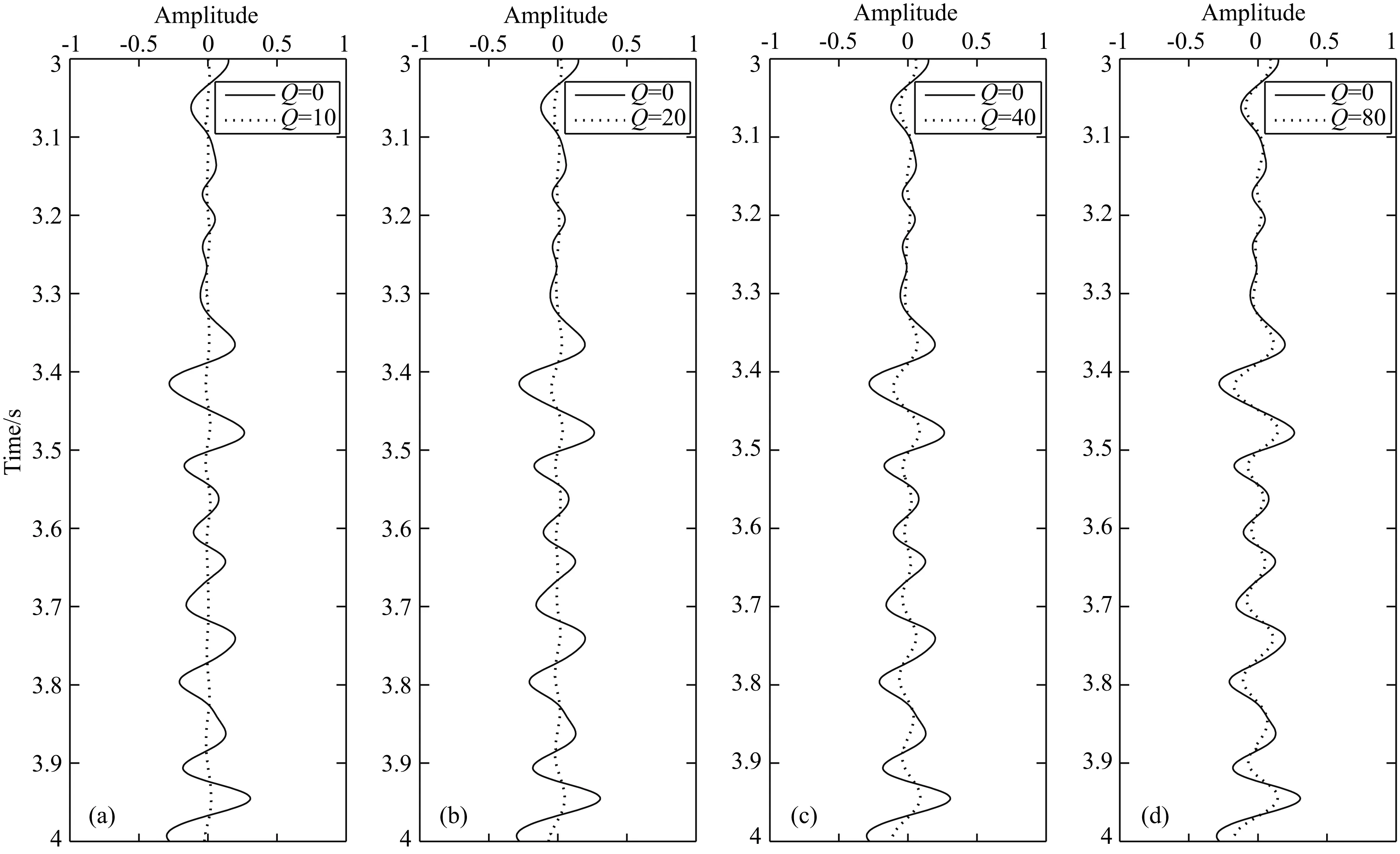
图13　2400 m处3-4s单道对比(a) Q=0与Q=10单道对比; (b) Q=0与Q=20单道对比; (c) Q=0与Q=40单道对比; (d) Q=0与Q=80单道对比.Fig.13　Contrast of single traces (Distance=2400 meters, 3～4 s)

对于实际数据应用而言，本文方法尚需进一步探索.若采用二维算法，则需要对实际数据的振幅和相位进行校正，因此有必要在此基础上开展三维算法.同时，三维的大数据处理对算法适应性提出更高的要求，将GPU和MPI相结合是一种有效的方式，显然时域全波形反演方法更加适合.

Almomin A, Biondi B. 2012. Tomographic full waveform inversion: Practical and computationally feasible approach. ∥ 82nd Annual International Meeting. SEG, 1-5, doi: 10.1190/segam2012-0976.1.

Bai J Y, Yingst D, Bloor R, et al. 2014. Viscoacoustic waveform inversion of velocity structures in the time domain.Geophysics, 79(3): R103-R119, doi: 10.1190/geo2013-0030.1. Biondi B, Almomin A. 2012. Tomographic full waveform inversion (TFWI) by combining full waveform inversion with wave-equation migration velocity analysis. ∥ 82nd Annual International Meeting. SEG, 1-5, doi: 10.1190/segam2012-0275.1. Boonyasiriwat C, Zhan G, Hadwiger M, et al. 2010. Multisource reverse-time migration and full-waveform inversion on a GPGPU. ∥ 72nd EAGE Conference and Exhibition. SPE, EAGE. Brenders A J, Pratt R G. 2007. Full-waveform tomography for lithospheric imaging: Results from a blind test in a realistic crustal model.GeophysicalJournalInternational, 168(1): 133-151, doi: 10.1111/j.1365-246X.2006.03156.x.

Bunks C, Saleck F M, Zaleski S, et al. 1995. Multiscale seismic waveform inversion.Geophysics, 60(5): 1457-1473, doi: 10.1190/1.1443880. Gauthier O, Virieux J, Tarantola A. 1986. Two-dimensional nonlinear inversion of seismic waveforms: Numerical results.Geophysics, 51(7): 1387-1403, doi: 10.1190/1.1442188.

Hager W W, Zhang H C. 2006. A survey of nonlinear conjugate gradient methods.PacificJournalofOptimization, 2(1): 35-58.

Li B, Liu H W, Liu G F, et al. 2010. Computational strategy of seismic pre-stack reverse time migration on CPU/GPU.ChineseJ.Geophys. (in Chinese), 53(12): 2938-2943, doi: 10.3969/j.issn.0001-5733.2010.12.017.

Liu H W, Liu H, Li B, et al. 2011. Pre-stack reverse time migration for rugged topography and GPU acceleration technology.ChineseJ.Geophys. (in Chinese), 54(7): 1883-1892, doi: 10.3969/j.issn.0001-5733.2011.07.022. Liu S W, Wang H Z, Chen S C, et al. 2013. Implementation strategy of 3D reverse time migration on GPU/CPU clusters.ChineseJ.Geophys. (in Chinese), 56(10): 3487-3496, doi: 10.6038/cjg20131023.

Luo J R, Wu R S. 2013. Envelope inversion-Some application issues. ∥ 83rd Annual International Meeting. SEG, 1042-1047, doi: 10.1190/segam2013-0718.1.

Moghaddam P P, Keers H, Herrmann F J, et al. 2013. A new optimization approach for source-encoding full-waveform inversion.Geophysics, 78(3): R125-R132, doi: 10.1190/geo2012-0090.1.

Pratt R G. 1999a. Seismic waveform inversion in the frequency domain, Part I: Theory and verification in a physical scale model.Geophysics, 64(3): 888-901, doi: 10.1190/1.1444597. Pratt R G, Shipp R M. 1999b. Seismic waveform inversion in the frequency domain, Part 2: Fault delineation in sediments using crosshole data.Geophysics, 64(3): 902-914, doi: 10.1190/1.1444598.

Shi Y, Liu H, Zou Z. 2010. Surface-related multiples prediction based on wave equation and adaptive subtraction investigation.ChineseJ.Geophys. (in Chinese), 53(7): 1716-1724, doi: 10.3969/j.issn.0001-5733.2010.07.023.

Shi Y, Wang W H, Li Y, et al. 2013. 3D surface-related multiple prediction approach investigation based on wave equation.ChineseJ.Geophys. (in Chinese), 56(6): 2023-2032, doi: 10.6038/cjg20130623.

Shin C, Jang S, Min D J. 2001. Improved amplitude preservation for prestack depth migration by inverse scattering theory.GeophysicalProspecting, 49 (5): 592-606, doi: 10.1046/j.1365-2478.2001.00279.x.Shin C, Cha Y H. 2008. Waveform inversion in the Laplace domain.GeophysicalJournalInternational, 173(3): 922-931, doi: 10.1111/j.1365-246X.2008.03768.x.

Shin C, Cha Y H. 2009. Waveform inversion in the Laplace-Fourier domain.GeophysicalJournalInternational, 177(3): 1067-1079, doi: 10.1111/j.1365-246X.2009.04102.x. Shin J, Ha W, Jun H, et al. 2014. 3D Laplace-domain full waveform inversion using a single GPU card.Computers&Geosciences, 67: 1-13, doi: 10.1016/j.cageo.2014.02.006.Tarantola A. 1984. Inversion of seismic reflection data in the acoustic approximation.Geophysics, 49(8): 1259-1266, doi: 10.1190/1.1441754. Tarantola A. 1986. A strategy for nonlinear elastic inversion of seismic reflection data.Geophysics, 51(10): 1893-1903, doi: 10.1190/1.1442046.

Wu R S, Luo J R, Wu B Y. 2013. Ultra-low-frequency information in seismic data and envelop inversion. ∥ 83nd Annual International Meeting. SEG, 3078-3082, doi: 10.1190/segam2013-0825.1.Wu R S, Luo J R, Wu B Y. 2014. Seismic envelope inversion and modulation signal model.Geophysics, 79(3): WA13-WA24, doi: 10.1190/geo2013-0294.1. Yang P L, Gao J H, Wang B L. 2014. RTM using effective boundary saving: A staggered grid GPU implementation.Computers& Geosciences, 68: 64-72,doi: 10.1016/j.cageo.2014.04.004.YangPL,GaoJH,WangBL. 2015.Agraphicsprocessingunitimplementationoftime-domainfull-waveforminversion. Geophysics, 80(3):F31-F39,doi: 10.1190/GEO2014-0283.1.

附中文参考文献

李博, 刘红伟, 刘国峰等. 2010. 地震叠前逆时偏移算法的CPU/GPU实施对策. 地球物理学报, 53(12): 2938-2943, doi: 10.3969/j.issn.0001-5733.2010.12.017.

刘红伟, 刘洪, 李博等. 2011. 起伏地表叠前逆时偏移理论及GPU加速技术. 地球物理学报, 54(7): 1883-1892, doi: 10.3969/j.issn.0001-5733.2011.07.022.

刘守伟, 王华忠, 陈生昌等. 2013. 三维逆时偏移GPU/CPU机群实现方案研究. 地球物理学报, 56(10): 3487-3496, doi: 10.6038/cjg20131023.

石颖, 刘洪, 邹振. 2010. 基于波动方程表面多次波预测与自适应相减方法研究. 地球物理学报, 53(7): 1716-1724, doi: 10.3969/j.issn.0001-5733.2010.07.023.

石颖, 王维红, 李莹等. 2013. 基于波动方程三维表面多次波预测方法研究. 地球物理学报, 56(6): 2023-2032, doi: 10.6038/cjg20130623.

(本文编辑胡素芳)

Time domain full waveform inversion based on frequency attenuation

GUO Xue-Bao1,2， LIU Hong1,2， SHI Ying3

1KeyLaboratoryofPetroleumResourcesResearch,InstituteofGeologyandGeophysics,ChineseAcademyofSciences,Beijing100029，China2InstituteofGeologyandGeophysics,ChineseAcademyofSciences,Beijing100029，China3NortheastPetroleumUniversity,Daqing163318，China

Because the full frequency range information is used in time domain full waveform inversion, different wavelengths can not be reconstructed gradually. So it is easy to fall into local minimum value. In this paper, we extract different frequency bands from seismic data by Fourier transform. Different level of high frequency components can be separated by attenuating corresponding frequency ranges, and time domain full waveform inversion is implemented from low to high frequency. At the same time, latter arrivals are attenuated and this can reduce the interference in the process of shallow part inversion. Fourier transform is only required for the shot gathers, compared with hybrid domain inversion, and don′t need to extract the corresponding frequency components of all wavefields. In the aspect of computing efficiency, the algorithm is based on GPU and uses cufft to further improve the efficiency of calculation. Through the Marmouse model test, the validity of this method is verified.

Time domain full waveform inversion; Frequency attenuation; Low frequency; GPU

10.6038/cjg20161022.

国家高技术研究发展计划(863计划)(2012AA061202)，国家自然科学基金项目(41574117, 41474118)，黑龙江省杰出青年科学基金项目(JC2016006)以及大连理工大学国家重点实验室开放基金项目(LP1509)联合资助.

郭雪豹，1990年生，在读博士，主要从事地震数据成像相关研究工作.E-mail：guoxuebao1108@163.com

10.6038/cjg20161022

P631

2015-11-16，2016-06-28收修定稿

郭雪豹， 刘洪， 石颖. 2016. 基于频域衰减的时域全波形反演. 地球物理学报，59(10):3777-3787,

Guo X B， Liu H， Shi Y. 2016. Time domain full waveform inversion based on frequency attenuation.ChineseJ.Geophys. (in Chinese),59(10):3777-3787,doi:10.6038/cjg20161022.